Brillouin Zones

History

The concept of a Brillouin zone was first developed by Léon Brillouin (1889-1969), a French physicist. During his work on the propagation of electron waves in a crystal lattice, he introduced the concept of Brillouin zone in 1930.\(^{[5]}\) Quantum mechanical perturbations techniques by Brillouin and by Eugene Wigner resulted in what is known as the Brillouin-Wigner formula.\(^{[6]}\) He also made contributions to quantum mechanics, radio wave propagation in the atmosphere, solid state physics, and information theory. He also studied the propagation of monochromatic light waves and their interaction with acoustic waves, i.e., scattering of light with a frequency change, which became known as Brillouin scattering.

Brillouin Zones

A Brillouin zone is defined as a Wigner-Seitz primitive cell in the reciprocal lattice. The first Brillouin zone is the smallest volume entirely enclosed by planes that are the perpendicular bisectors of the reciprocal lattice vectors drawn from the origin. The concept of Brillouin zone is particularly important in the consideration of the electronic structure of solids. There are also second, third, etc., Brillouin zones, corresponding to a sequence of disjoint regions (all with the same volume) at increasing distances from the origin, but these are used more rarely. As a result, the first Brillouin zone is often called simply the Brillouin zone. (In general, the n-th Brillouin zone consist of the set of points that can be reached from the origin by crossing n − 1 Bragg planes.) \(^{[1]}\)

The region in k-space (here an imaginary plane whose rectangular coordinates are kx and ky) that low-k electrons can occupy without being diffracted is called first Brillouin Zone, shown in Figure \(\PageIndex{1}\)​​​​​​​. The second Brillouin zone is also Shown; it contains electrons with \(k\) values from \(\pi/a\) to \(2\pi/a\) for electrons moving in the ±x and ±y directions, with the possible range of k values narrowing as the diagonal directions are approached.\(^{[3]}\)

Figure \(\PageIndex{1}\) The first and second Brillouin zones of a two-dimensional square lattice

Further Brillouin zones can be constructed in the same manner. The extension of this analysis to actually three-dimensional structure leads to Brillouin zones such as those shown in the Figure \(\PageIndex{2}\).

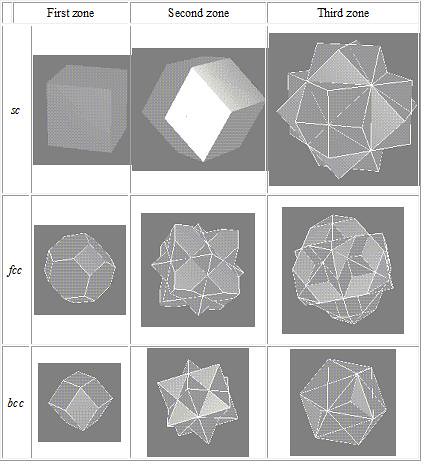
Figure \(\PageIndex{2}\) The first three Brillouin zones for some lattices are illustrated\(^{[2,10]}\)

Energy and Momentum

\[ \begin{align} E=\frac{p^{2}}{2m} \end{align}\]

and hence to its wave number \(k\) by

Energy and wave number

\[ \begin{align} E=\dfrac{\hbar^{2}k^{2}}{2m} \end{align}\]

In the case of an electron in a crystal for which \(k\ll \pi/a\), there is practically no interaction with the lattice, and Eq. (2) is valid. Since the energy of such an electron depends on \(k^2\), the contour lines of constant energy in a two-dimensional \(k\) space are simply circles of constant \(k\), as in the Figure \(\PageIndex{3}\), for such \(k\) values.

Figure \(\PageIndex{3}\) Energy contours in electronvolts in the first and second Brillouin zones of a hypothetical square lattice

With increasing k the constant-energy contour lines become progressively closer together and also more and more distorted. The reason for the first effect is merely that E varies with \(k^2\). The reason for the second is almost equally straightforward. The closer an electron is to the boundary of a Brillouin zone in \(k\)-space, the closer it is to being reflected by the actual crystal lattice. But in particle terms the reflection occurs by virtue of the interaction of the electron with the periodic array of positive ions that occupy the lattice points, and the stronger the interaction, the more the electron's energy is affected. \(^{[3,4]}\)

Origin of Forbidden Bands

Figure \(\PageIndex{4}\) shows how E varies with k in the x direction. As \(k\) approaches \(k^2\), \(E\) increases more slowly than \({\hbar}^2k^2/2m\), the free-particle Figure . At \(k=\pi/a\), E has two values, the lower belonging to the first Brillouin zone and the higher to the second zone. There is a definite gap between the possible energies in the first and second Brillouin zones which corresponds to a forbidden band. The same pattern continues as successively higher Brillouin zones are reached.

Figure \(\PageIndex{4}\) Electron energy E wave number \(k\) in the \(k_{x}\) direction. The dash line shows how E varies with k for a free electron, as given by Eq. (2).\(^{[11]}\)

The energy discontinuity at the boundary of a Brillouin zone follows from the fact that the limiting values of k corresponds to standing waves rather than traveling waves. For clarity we consider electrons moving in the x direction; extending the argument to any other direction is straightforward. When \(k=\pm \pi/a\), as we have seen, the waves are Bragg-reflected back and forth, and so the only solutions of Schrödinger’s equation consist of standing waves whose wavelength is equal to the periodicity of the lattice. There are two possibilities for these standing waves for n = 1, namely,

\[\begin{align} \psi_{1}=A\sin\dfrac{\pi x}{a} \end{align}\]

\[\begin{align} \psi_{2}=A\cos\dfrac{\pi x}{a} \end{align} \]

The probabilities densities \(|\psi_{1}|^{2}\) and \(|\psi_{2}|^{2}\) are plotted in Figure \(\PageIndex{5}\). Evidently \(|\psi_{1}|^{2}\) has its minima at the lattice points occupied by the positive ions, while \(|\psi_{2}|^{2}\) has its maxima at the lattice points. Since the charge density corresponding to an electron wave function \(\psi\) is \(-e|\psi|^{2}\), the charge density in the case of \(\psi_{1}\) is concentrated at the positive ions. The potential energy of an electron in a lattice of positive ions is greatest midway between each pair of ions and least at the ions themselves, so the electron energies \(E_1\) and \(E_2\) associated with the standing waves \(\psi_{1}\) and \(\psi_{2}\) are different. No other solutions are possible when \(k=\pm\pi/a\) and accordingly no electron can have an energy between \(E_1\) and \(E_2\).

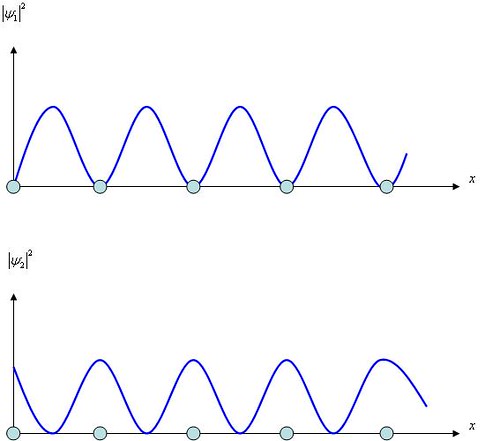
Figure \(\PageIndex{5}\) Distributions of the probability densities \(\psi_{1}|^{2}\) and \(|\psi_{2}|^{2}\)

Irreducible wedge of Brillouin zone

First Brillouin zone (BZ) represents the central (Wigner-Seitz) cell of the reciprocal lattice. It contains all points nearest to the enclosed reciprocal lattice point. The boundaries of the first BZ are determined by planes which are perpendicular to the reciprocal lattice vectors pointing from the center of the cell to the 14 lattice points nearest to the origin of the cell at their midpoints\(^{[7]}\). The 14 faces are

\[ \begin{align} \mid{K}_{x}\mid+ \mid{K}_{y}\mid+ \mid{K}_{z}\mid=\frac{3}{2}\frac{2\pi}{a_{0}} , \mid{K}_{x}\mid=\frac{2\pi}{a_{0}} , \mid{K}_{y}\mid=\dfrac{2\pi}{a_{0}}, and \mid{K}_{z}\mid=\frac{2\pi}{a_{0}} \end{align} \]

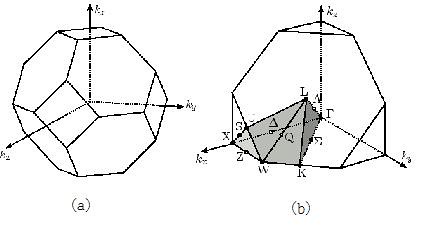
Figure \(\PageIndex{6}\) (a) First Brillouin zone of the fcc lattice (b) The inset gives the locations of certain symmetry points and symmetry lines in the BZ.

In Figure \(\PageIndex{6}\) (a) the first BZ is depicted. It has a volume \(\Omega_{0}\) of \(4(2\pi/a_{0})\)\(^{[8]}\). Due to the translational invariance of the lattice the wave functions and the energy bands are periodic in the reciprocal space and it is sufficient to consider only the first BZ for band structure calculations\(^{[9]}\).

For example, the diamond structure is invariant not only under translations, but also under several other symmetry operations such as reflections, rotations, or inversion. These symmetry operations are usually denoted as point operations, since they leave at least one point of the lattice invariant, which is not the case for translations. The set of all point operations for a particular crystal structure forms a group which is denoted as point group. The point group of the diamond structure has 48 symmetry elements which are reflected in the symmetry of the first BZ. A quick examination (see Figure \(\PageIndex{6}\)) shows that the BZ is invariant under various rotations, for example 90^o rotations about the \(k_x\), \(k_y\) and \(k_z\) axes and under reflections through certain planes.

The point symmetries of the crystal structure are mirrored in the crystal potential, and hence in the one-particle Hamiltonian used for band structure calculations. Two important consequences for the electron band structure arise:

• Wave functions can be expressed in such a form that they have definite transformation properties under symmetry operations of the crystal. Certain matrix elements of operators can be shown to vanish and selection rules can be deduced, when classifying the wave functions according to their symmetry.
• The energy bands possess the full point symmetry of the point group of the crystal. The symmetries can be exploited to restrict the band structure calculation to a fraction of only 1/48th of the first BZ. This fraction is called irreducible wedge of the BZ.

The irreducible wedge of the fcc lattice is depicted in Figure \(\PageIndex{6}\). (b) It has six corners

connected via symmetry lines

By convention upper case Greek letters are used for points and lines inside the first BZ, whereas roman letters denote points and lines on the surface of the first BZ. Here, the points \(U\) and \(K\) can be interchanged, since they are equivalent in the reciprocal space.

References

1. http://en.Wikipedia.org/wiki/Brillouin_zone
2. http://phycomp.technion.ac.il/~nika/brillouin_zones.html
3. A. Beiser. “ Concepts of Modern Physics 6th edition ” p. 371-373 (ISBN 007-123460-8)
4. M. Ali Omar. “Elementary Solid State Physic” p.48, 94. (ISBN 0- 201-60733-6)
5. Léon Brillouin Les électrons dans les métaux et le classement des ondes de de Broglie correspondantes Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences, 191, 292 (1930). (original article)
6. Brillouin thesis title: La théorie des solides et les quanta, as cited in Mehra, Volume 5, Part 2, 579.
7. http://www.iue.tuwien.ac.at/phd/ungersboeck/node27.html
8. "Physics of semiconductors and their heterostructures," McGraw-Hill, 1993.
9. P. Yu, and M. Cardona. "Fundamentals of Semiconductors," Springer, 2003.
10. E.Wigner and F. Seitz. "On the Constitution of Metallic Sodium" Phys. Rev. 43, 804 (1933)

Contributors and Attributions

• ContribMSE5317