7.4: Buoyancy effects- the baroclinic torque
- Page ID
- 18080
We now assume that the fluid is inviscid (\(ν = 0\)) but not homogeneous (\(\rho\) is allowed to vary). The momentum equation Equation 7.2.2 becomes
\[\frac{D \vec{u}}{D t}=\vec{g}-\frac{1}{\rho} \vec{\nabla} p,\label{eqn:1} \]
and once again we take its curl to form the vorticity equation. The first two terms are already computed:
\[\vec{\nabla} \times \frac{D \vec{u}}{D t}=\frac{D \vec{\omega}}{D t}-[\vec{\omega} \cdot \vec{\nabla}] \vec{u} \quad \text { and } \vec{\nabla} \times \vec{g}=0. \nonumber \]
The curl of the new term (obtained using identities 11 and 15 listed in appendix E) is:
\[\begin{aligned}
\vec{\nabla} \times\left(-\rho^{-1} \vec{\nabla} p\right) &=-\left(\vec{\nabla} \rho^{-1} \times \vec{\nabla} p+\rho^{-1} \vec{\nabla} \times \vec{\nabla} p\right) \\
&=-\vec{\nabla} \rho^{-1} \times \vec{\nabla} p \\
&=\frac{1}{\rho^{2}} \vec{\nabla} \rho \times \vec{\nabla} p.
\end{aligned} \nonumber \]
This is called the baroclinic torque:
\[\vec{B}=\frac{1}{\rho^{2}} \vec{\nabla} \rho \times \vec{\nabla} p,\label{eqn:2} \]
and the vorticity equation is
\[\frac{D \vec{\omega}}{D t}=[\vec{\omega} \cdot \vec{\nabla}] \vec{u}+\vec{B}. \nonumber \]
The baroclinic torque \(\vec{B}\) is the mechanism by which density variations influence vorticity. This torque is zero in the case of a barotropic fluid (section 6.6.2), where \(\rho = \rho(p)\), because \(\vec{\nabla}\rho\) and \(\vec{\nabla}p\) are then parallel.
To understand the mechanism physically, we first separate the pressure into two parts: hydrostatic and nonhydrostatic:
\[p=p_{H}+p^{*}. \nonumber \]
The hydrostatic part is defined by the condition of hydrostatic balance:
\[\vec{\nabla} p_{H}=\rho \vec{g}, \nonumber \]
so that
\[\vec{\nabla} p=\rho \vec{g}+\vec{\nabla} p^{*}.\label{eqn:3} \]
Substituting this decomposition into the momentum equation Equation \(\ref{eqn:1}\) gives
\[\frac{D \vec{u}}{D t}=-\frac{1}{\rho} \vec{\nabla} p^{*}.\label{eqn:4} \]
So the hydrostatic pressure simply holds up the weight of the water at each point while the nonhydrostatic pressure actually causes motion.
Now we substitute the decomposition Equation \(\ref{eqn:3}\) into Equation \(\ref{eqn:2}\):
\[\begin{align}
\vec{B} &=\frac{1}{\rho^{2}} \vec{\nabla} \rho \times \vec{\nabla} p \\
&=\frac{1}{\rho^{2}} \vec{\nabla} \rho \times\left(\rho \vec{g}+\vec{\nabla} p^{*}\right)\label{eqn:5} \\
&=\underbrace{\frac{1}{\rho} \vec{\nabla} \rho \times \vec{g}}_{\text {buoyancy }}+\underbrace{\frac{1}{\rho^{2}} \vec{\nabla} \rho \times \vec{\nabla} p^{*}.}_{\text {inertia }}\label{eqn:6}
\end{align} \nonumber \]
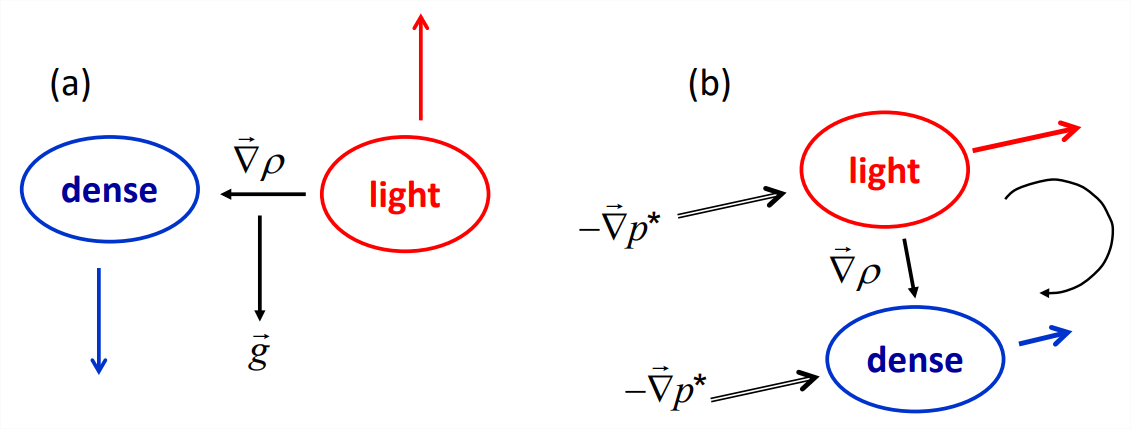
Evidently, the baroclinic torque has two parts. Illustrated in Figure (\(\PageIndex{1}\)), these correspond to two distinct mechanisms by which density differences can alter the vorticity. The buoyancy term quantifies the tendency for dense fluid to sink and light fluid to rise. It is nonzero if the density gradient has a component perpendicular to gravity, as in Figure \(\PageIndex{1}\)a. Using the right-hand rule, verify for yourself that the cross product \(\vec{\nabla}\rho \times\vec{g}\) is directed out of the page. The buoyancy term therefore imparts a counterclockwise rotation to the flow, consistent with the vertical motion of the fluid parcels.
The inertia term results from the fact that a force (e.g., \(-\vec{\nabla}p^*\)), acting on fluid parcels of different density, produces different rates of acceleration (Figure \(\PageIndex{1}\)b). The term is nonzero if the density gradient has a component perpendicular to the pressure gradient force. Again, use the right-hand rule to check that the inertial torque is directed into the page and therefore generates clockwise vorticity.
Which term is more important? Inspection of Equation \(\ref{eqn:5}\) shows that the inertial term is small compared to the buoyancy term if \(|\vec{\nabla}p^*|/\rho\ll g\). The left-hand side of this inequality is just the net acceleration of the flow, as is shown by Equation \(\ref{eqn:4}\). Therefore, the buoyancy term dominates if the net acceleration is much less than the gravitational acceleration (“1 gee”, in aeronautical lingo). This is true of the slow motions caused by weak density gradients in the interior of the ocean or the atmosphere. For that reason, we often neglect the inertial term when describing such motions. This leads to the Boussinesq approximation (see Appendix G).
In contrast, air-water interfaces have large density gradients. Accelerations are therefore comparable to gravity (imagine a breaking wave, for example), and buoyancy and inertia are both important. These motions are the topic of the upcoming chapter.