4.6: Buoyancy and Stability
- Page ID
- 686
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\) 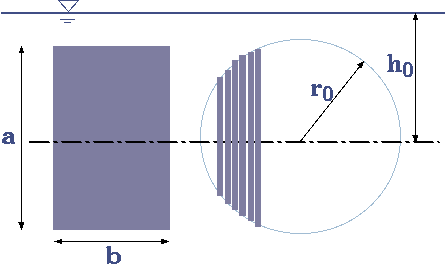
Fig. 4.34. Schematic of immersed cylinder
One of the oldest known scientific research on fluid mechanics relates to buoyancy due to question of money was carried by Archimedes. Archimedes principle is related to question of density and volume. While Archimedes did not know much about integrals, he was able to capture the essence. Here, because this material is presented in a different era, more advance mathematics will be used. While the question of the stability was not scientifically examined in the past, the floating vessels structure (more than 150 years ago) show some understanding. The total forces the liquid exacts on a body are considered as a buoyancy issue. To understand this issue, consider a cubical and a cylindrical body that is immersed in liquid and center in a depth of \(h_{0}\) as shown in Fig. 4.34. The force to hold the cylinder at the place must be made of integration of the pressure around the surface of the square and cylinder bodies. The forces on square geometry body are made only of vertical forces because the two sides cancel each other. However, on the vertical direction, the pressure on the two surfaces are different. On the upper surface the pressure is \(\rho g \left(h_{0} - a/2\right)\). On the lower surface the pressure is \(\rho g \left(h_{0} + a/2\right)\). The force due to the liquid pressure per unit depth (into the page) is \[F = \rho g \left(\left(h_{0} - a/2\right) - \left(h_{0} + a/2\right)\right)llb = -\rho g a b l l = -\rho g V \] In this case the \(ll\) represents a depth (into the page). Rearranging equation 1 to be \[\frac{F}{V} = \rho g \] The force on the immersed body is equal to the weight of the displaced liquid. This analysis can be generalized by noticing two things. All the horizontal forces are canceled. Any body that has a projected area that has two sides, those will cancel each other. Another way to look at this point is by approximation. For any two rectangle bodies, the horizontal forces are canceling each other. Thus even these bodies are in contact with each other, the imaginary pressure make it so that they cancel each other. On the other hand, any shape is made of many small rectangles. The force on every rectangular shape is made of its weight of the volume. Thus, the total force is made of the sum of all the small rectangles which is the weight of the sum of all volume.
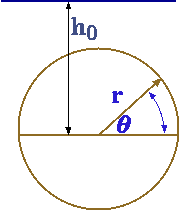
Fig. 4.35. The floating forces on immersed cylinder.
In illustration of this concept, consider the cylindrical shape in Fig. 4.34. The force per area (see Fig. 4.35) is \[dF = \rho g \left(h_{0} - r sin \theta \right) sin \theta r d\theta \] The total force will be the integral of the equation 1 \[F = \int_{0}^{2\pi} \rho g \left(h_{0} - r sin \theta \right) r d\theta sin \theta \] Rearranging equation 3 transforms it to \[F = rg\rho \int_{0}^{2\pi} \left(h_{0} - rsin\theta\right) sin \theta d\theta \] The solution of equation 5 is \[F = -\pi r^{2} \rho g \] The negative sign indicate that the force acting upwards. While the horizontal force is \[F_{v} = \int_{0}^{2\pi} \left(h_{0} - rsin\theta\right) cos \theta d\theta = 0 \]
To what depth will a long log with radius, \(r\), a length, \(ll\) and density, \(\rho_w\) in liquid with density, \(\rho_l\). Assume that \(\rho_l>\rho_w\). You can provide that the angle or the depth.
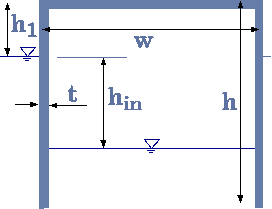
Fig. 4.36. Schematic of a thin wall floating body.
Typical examples to explain the buoyancy are of the vessel with thin walls put upside down into liquid. The second example of the speed of the floating bodies. Since there are no better examples, these examples are a must.
A cylindrical body, shown in Figure 4.36, is floating in liquid with density, \(ρ_l\). The body was inserted into liquid in a such a way that the air had remained in it. Express the maximum wall thickness, \(t\), as a function of the density of the wall, ρs liquid density, \(ρ_l\) and the surroundings air temperature, \(T_1\) for the body to float. In the case where thickness is half the maximum, calculate the pressure inside the container. The container diameter is \(w\). Assume that the wall thickness is small compared with the other dimensions (\(t<<w\) and \(t<<h\)).
The air mass in the container is
\[
m_{air} = \overbrace{\pi\,w^2\,h}^{V}
\overbrace{\dfrac{P_{atmos}}{R\,T}} ^{\rho_{air}}
\]
\[
m_{container} =
\left(\overbrace{\pi\,w^2 + 2\,\pi\,w\,h}^{A}\right)
\,t \,\rho_{s}
\]
The liquid amount enters into the cavity is such that the air pressure in the cavity equals to the pressure at the interface (in the cavity). Note that for the maximum thickness, the height, \(h_1\) has to be zero. Thus, the pressure at the interface can be written as
\[
P_{in} = \rho_{l}\,g\,h_{in}
\]
On the other hand, the pressure at the interface from the air point of view (ideal gas model) should be
\[
P_{in} = \dfrac{m_{air}\,R\,T_1}
{\underbrace{ h_{in}\,\pi\,w^2}_{V}}
\]
Since the air mass didn't change and it is known, it can be inserted into the above equation.
\[
\rho_{l}\,g\,h_{in}+ P_{atmos} = P_{in} =
\dfrac
Callstack:
at (Bookshelves/Civil_Engineering/Fluid_Mechanics_(Bar-Meir)/04:_Fluids_Statics/4.6:_Buoyancy_and_Stability), /content/body/div[3]/div/p[6]/span, line 1, column 1
\] And the solution for \(h_{in}\) is
\[
h_{in}= -
\dfrac{P_{atmos}
+\sqrt{4\,g\,h\,P_{atmos}\,\rho_l+{P_{atmos}}^{2}}
}{2\,g\,\rho_l}
\]
and
\[
h_{in} =
\dfrac
{\sqrt{4\,g\,h\,P_{atmos}\,\rho_l+{P_{atmos}}^{2}}-P_{atmos}}
{2\,g\,\rho_l}
\]
The solution must be positive, so that the last solution is the only physical solution.
Advance Material
Calculate the minimum density an infinitely long equilateral triangle (three equal sides) has to be so that the sharp end is in the water.
The solution demonstrates that when \(h \longrightarrow 0\) then \(h_{in} \longrightarrow 0\). When the gravity approaches zero (macro gravity) then
\begin{align*}
h_{in}= \dfrac{P_{atmos}}{\rho_l\,g}+h
-\dfrac
Callstack:
at (Bookshelves/Civil_Engineering/Fluid_Mechanics_(Bar-Meir)/04:_Fluids_Statics/4.6:_Buoyancy_and_Stability), /content/body/div[5]/div/p/span[1], line 1, column 2
+\dfrac{2\,{h}^{3}\,{\rho_l}^{2}\,{g}^{2}}
Callstack:
at (Bookshelves/Civil_Engineering/Fluid_Mechanics_(Bar-Meir)/04:_Fluids_Statics/4.6:_Buoyancy_and_Stability), /content/body/div[5]/div/p/span[2], line 1, column 9
-\dfrac{5\,{h}^{4}\,{\rho_l}^{3}\,{g}^{3}}
Callstack:
at (Bookshelves/Civil_Engineering/Fluid_Mechanics_(Bar-Meir)/04:_Fluids_Statics/4.6:_Buoyancy_and_Stability), /content/body/div[5]/div/p/span[3], line 1, column 9
+\cdots
\end{align*}
This "strange'' result shows that bodies don't float in the normal sense. When the floating is under vacuum condition, the following height can be expanded into
\begin{align*}
h_{in}=\sqrt{\dfrac{h\,P_{atmos}}
Callstack:
at (Bookshelves/Civil_Engineering/Fluid_Mechanics_(Bar-Meir)/04:_Fluids_Statics/4.6:_Buoyancy_and_Stability), /content/body/div[5]/div/p/span[4], line 1, column 2
+\dfrac{P_{atmos}}{2\,g\,\rho_l}
+ \cdots
\end{align*}
which shows that the large quantity of liquid enters into the container as it is expected. Archimedes theorem states that the force balance is at displaced weight liquid (of the same volume) should be the same as the container, the air. Thus,
\begin{align*}
\overbrace{\pi\, w^2\, (h-h_{in}) \,g}^{\text{net displayed<br>water}}=
\overbrace{\left(\pi\,w^2 + 2\,\pi\,w\,h\right)\,t\,\rho_{s}\,g}
^{\text{container}}
+
\overbrace
Callstack:
at (Bookshelves/Civil_Engineering/Fluid_Mechanics_(Bar-Meir)/04:_Fluids_Statics/4.6:_Buoyancy_and_Stability), /content/body/div[5]/div/p/span[5], line 1, column 1
\end{align*}
If air mass is neglected the maximum thickness is
\begin{align*}
t_{max} =
\dfrac{
2\,g\,h\,w\,\rho_l+P_{atmos}\,w
-w\,\sqrt{4\,gh\,P_{atmos}\,\rho_l+{P_{atmos}}^{2}}
}
{\left( 2\,g\,w+4\,g\,h\right) \,\rho_l\,\rho_s}
\end{align*}
The condition to have physical value for the maximum thickness is
\begin{align*}
2\,g\,h\,\rho_l+P_{atmos} \ge
\sqrt{4\,gh\,P_{atmos}\,\rho_l+{P_{atmos}}^{2}}
\end{align*}
The full solution is
\begin{align*}
\begin{array}{cc}
t_{max} = &
-\dfrac{\left(
w\,R\,\sqrt{4\,gh\,P_{atmos}\,\rho_l+{P_{atmos}}^{2}}
-2\,g\,h\,w\,R\,\rho_l-P_{atmos}\,w\,R\right)
\,T_1+2\,g\,h\,P_{atmos}\,w\,\rho_l}
{\left( 2\,g\,w+4\,g\,h\right) \,R\,\rho_l\,\rho_s\,T_1}
\end{array}
\end{align*}
In this analysis the air temperature in the container immediately after insertion in the liquid has different value from the final temperature. It is reasonable as the first approximation to assume that the process is adiabatic and isentropic. Thus, the temperature in the cavity immediately after the insertion is
\begin{align*}
\dfrac{T_i}{T_f} =
\left( \dfrac{P_i}{P_f} \right)
\end{align*}
The final temperature and pressure were calculated previously. The equation of state is
\begin{align*}
P_i = \dfrac{m_{air}\,R\,T_i}{V_i}
\end{align*}
The new unknown must provide additional equation which is
\begin{align*}
V_i = \pi\,w^2\,h_{i}
\end{align*}
Thickness Below The Maximum
For the half thickness \(t= \dfrac{t_{max}}{2}\) the general solution for any given thickness below maximum is presented. The thickness is known, but the liquid displacement is still unknown. The pressure at the interface (after long time) is
\begin{align*}
\rho_l \,g \, h_{in} +P_{atmos} =
\dfrac{\pi\,w^2\,h \dfrac{P_{atmos}}{R\,T_1} R\, T_1}
{\left(h_{in}+h_1\right)\,\pi\,w^2}
\end{align*}
which can be simplified to
\begin{align*}
\rho_l \, g\,h_{in} + P_{atmos} =
\dfrac{h\,P_{atmos}}{h_{in}+h_1}
\end{align*}
The second equation is Archimedes' equation, which is
\begin{align*}
\pi\,w^2\left(h-h_{in} -h_1\right) =
\left( \pi\,w^2 +2\,\pi\,w\,h)\,t\,\rho_s\,g \right)
+\pi\,w^2\,h\,\left( \dfrac{P_{atmos}}{R\,T_1}\right)\,g
\end{align*}
End Advance Material
A body is pushed into the liquid to a distance, \(h_0\) and left at rest. Calculate acceleration and time for a body to reach the surface. The body's density is \(α\, ρ_l\), where \(α\) is ratio between the body density to the liquid density and (\(0<α<1\)). Is the body volume important?
The net force is
\begin{align*}
F = \overbrace{V\,g\,\rho_l}^{\text{liquid weight}} -
\overbrace{V\,g\,\alpha\,\rho_l}^{\text{body weight}} =
V\,g\, \rho_l \,( 1 -\alpha)
\end{align*}
But on the other side the internal force is
\begin{align*}
F = m\,a = \overbrace{V\,\alpha \rho_l}^{m}\, a
\end{align*}
Thus, the acceleration is
\begin{align*}
a = g \left( \dfrac{1-\alpha}{\alpha}\right)
\end{align*}
If the object is left at rest (no movement) thus time will be (\(h=1/2\,a\,t^2\))
\begin{align*}
t = \sqrt{\dfrac{2\,h \alpha}{g(1-\alpha)}}
\end{align*}
If the object is very light (\(\alpha \longrightarrow 0\)) then
\begin{align*}
t_{min} =
\sqrt{\dfrac{2\,h\,\alpha}{g}}
+\dfrac{\sqrt{2\,g\,h}\;{\alpha}^{\dfrac{3}{2}}} {2\,g}
+\dfrac{3\,\sqrt{2\,g\,h}\,{\alpha}^{\dfrac{5}{2}}}{8\,g}
+\dfrac{5\,\sqrt{2\,g\,h}\,{\alpha}^{\dfrac{7}{2}}}{16\,g}
+\cdots
\end{align*}
From the above equation, it can be observed that only the density ratio is important. This idea can lead to experiment in "large gravity'' because the acceleration can be magnified and it is much more than the reverse of free falling.
In some situations, it is desired to find equivalent of force of a certain shape to be replaced by another force of a "standard'' shape. Consider the force that acts on a half sphere. Find equivalent cylinder that has the same diameter that has the same force.
The force act on the half sphere can be found by integrating the forces around the sphere. The element force is
\[
dF = (\rho_L - \rho_S) \, g\, \overbrace{r\, \cos\phi\, \cos\theta}^{h}
\overbrace{\cos\theta\,\cos\phi\,
\overbrace{r^2\,d\theta\,d\phi}^{dA} }^{dA_x}
\]
The total force is then
\[
F_x = \int_0^{\pi} \int_0^{\pi}
(\rho_L - \rho_S) \, g\, {\cos^2\phi \cos^2\theta} \,
{r^3\,d\theta\,d\phi}
\]
\[ F_s = \dfrac
Callstack:
at (Bookshelves/Civil_Engineering/Fluid_Mechanics_(Bar-Meir)/04:_Fluids_Statics/4.6:_Buoyancy_and_Stability), /content/body/div[9]/div/p[4]/span, line 1, column 1
=
\cancel{\pi}\,\cancel{r^2} \, \cancel{(\rho_L - \rho_S)}\,h
\] Thus, the height is
\[
\dfrac{h}{r} = \dfrac{\pi}{4}
\]
In the introduction to this section, it was assumed that above liquid is a gas with inconsequential density. Suppose that the above layer is another liquid which has a bit lighter density. Body with density between the two liquids, \(ρ_l < ρ_s < ρ_h\) is floating between the two liquids. Develop the relationship between the densities of liquids and solid and the location of the solid cubical. There are situations where density is a function of the depth. What will be the location of solid body if the
In the discussion to this section, it was shown that net force is the body volume times the the density of the liquid. In the same vein, the body can be separated into two: one in first liquid and one in the second liquid. In this case there are two different liquid densities. The net force down is the weight of the body \(ρ_c\, h\, A\). Where \(h\) is the height of the body and \(A\) is its cross section. This force is balance according to above explanation by the two liquid as
\begin{align*}
\rho_c\, \cancel{h\, A} = \cancel{A \,h}\,\left( \alpha\,\rho_l + (1-\alpha) \rho_h \right)
\end{align*}
Where \(\alpha\) is the fraction that is in low liquid. After rearrangement it became
\begin{align*}
\alpha = \dfrac{ \rho_c - \rho_h}{\rho_l - \rho_h}
\end{align*}
the second part deals with the case where the density varied parabolically. The density as a function of \(x\) coordinate along \(h\) starting at point \(\rho_h\) is
\begin{align*}
\rho (x) = \rho_h - \left( \dfrac{x}{h} \right)^2 \left( \rho_h - \rho_l \right)
\end{align*}
Thus the equilibration will be achieved, \(A\) is canceled on both sides, when
\begin{align*}
\rho_c\, h = \int_{x_1}^{x_1+h} \left[ \rho_h - \left( \dfrac{x}{h} \right)^2
\left(\rho_h-\rho_l\right) \right]dx
\end{align*}
After the integration the equation transferred into
\begin{align*}
\rho_c\, h = \dfrac{\left( 3\,\rho_l-3\,\rho_h\right) \,{x1}^{2}+
\left( 3\,h\,\rho_l-3\,h\,\rho_h\right) \,x1+{h}^{2}\,\rho_l+2\,{h}^{2}\,\rho_h}
{3\,h}
\end{align*}
And the location where the lower point of the body (the physical), \(x_1\), will be at
\begin{align*}
X_1 = \dfrac{\sqrt{3}\,\sqrt{3\,h^2\,{\rho_l}^{2}+\left( 4\,\rho_c-6\,{h}^{2}\,\rho_h\right)
\,\rho_l+3\,{h}^{2}\,{\rho_h}^{2}-12\,\rho_c\,\rho_h}+3\,h\,\rho_l-3\,h\,\rho_h}
{6\,\rho_h-2\,\rho_l}
\end{align*}
For linear relationship the following results can be obtained.
\begin{align*}
x_1=\dfrac{h\,\rho_l+h\,\rho_h-6\,\rho_c}{2\,\rho_l-2\,\rho_h}
\end{align*}
In many cases in reality the variations occur in small zone compare to the size of the body. Thus, the calculations can be carried out under the assumption of sharp change. However, if the body is smaller compare to the zone of variation, they have to accounted for.
A hollow sphere is made of steel (\(ρ_s/ρ_w \cong 7.8\)) with a \(t\) wall thickness. What is the thickness if the sphere is neutrally buoyant? Assume that the radius of the sphere is \(R\). For the thickness below this critical value, develop an equation for the depth of the sphere.
The weight of displaced water has to be equal to the weight of the sphere
\[
\label{sphere:gov}
\rho_s\,\cancel{g} \, \dfrac{4\,\pi\, R^3}{3} =
\rho_w \,\cancel{g} \, \left( \dfrac{4\,\pi\, R^3}{3} -
\dfrac{4\,\pi\, \left(R-t\right)^3}{3} \right)
\]
after simplification equation (22) becomes
\[
\label{sphere:govR}
\dfrac{\rho_s\,R^3 }{\rho_w} =
3\,t\,{R}^{2}-3\,{t}^{2}\,R+{t}^{3}
\]
\begin{align*}
\label{sphere:completSol}
t_1&=&\left( -\dfrac{\sqrt{3}\,i}{2}-\dfrac{1}{2}\right) \,{\left( {\dfrac{\rho_s}{\rho_w}R}^{3}-
{R}^{3}\right) }^{\dfrac{1}{3}}+R \\
t_2&=&\left( \dfrac{\sqrt{3}\,i}{2}-\dfrac{1}{2}\right) \,{\left( {\dfrac{\rho_s}{\rho_w} R}^{3}-
{R}^{3}\right) }^{\dfrac{1}{3}}+R\\
t_3&=& R\,\left( \sqrt[3]{ \dfrac{\rho_s}{\rho_w} - 1 } + 1 \right)
\end{align*}
The first two solutions are imaginary thus not valid for the physical world. The last solution is the solution that was needed. The depth that sphere will be located depends on the ratio of \(t/R\) which similar analysis to the above. For a given ratio of \(t/R\), the weight displaced by the sphere has to be same as the sphere weight. The volume of a sphere cap (segment) is given by
\[
\label{sphere:capV}
V_{cap} = \dfrac{\pi\,h^2\,(3R-h)}{3}
\]
Where \(h\) is the sphere height above the water. The volume in the water is
\[
\label{sphere:waterV}
V_{water} = \dfrac{4\,\pi\, R^3}{3} - \dfrac{\pi\,h^2\,(3R-h)}{3}
= \dfrac{4\,\pi\,\left( R^3 -3\,R\,h^2 + h^3 \right) }{3}
\]
When \( V_{water}\) denotes the volume of the sphere in the water. Thus the Archimedes law is
\[
\label{sphere:archimedes1}
\dfrac{\rho_w\,4\,\pi\,\left( R^3 -3\,R\,h^2 + h^3 \right) }{3} =
\dfrac{\rho_s\,4\,\pi\,\left( 3\,t\,{R}^{2}-3\,{t}^{2}\,R+{t}^{3} \right)}{3}
\]
or
\[
\label{sphere:archimedes}
\left( R^3 -3\,R\,h^2 + h^3 \right) = \dfrac{\rho_w}{\rho_s}
\left( 3\,t\,{R}^{2}-3\,{t}^{2}\,R+{t}^{3} \right)
\]
The solution of (27) is
\[
\label{sphere:solArc}
h = \left( \dfrac{\sqrt{-fR\,\left( 4\,{R}^{3}-fR\right) }}{2}-\dfrac{fR-2\,{R}^{3}}{2}\right)^{\dfrac{1}{3}}
\\ + \dfrac
Callstack:
at (Bookshelves/Civil_Engineering/Fluid_Mechanics_(Bar-Meir)/04:_Fluids_Statics/4.6:_Buoyancy_and_Stability), /content/body/div[13]/div/p[8]/span[1], line 1, column 2
Callstack:
at (Bookshelves/Civil_Engineering/Fluid_Mechanics_(Bar-Meir)/04:_Fluids_Statics/4.6:_Buoyancy_and_Stability), /content/body/div[13]/div/p[8]/span[2], line 1, column 1
\] Where \(-fR = R^3- \dfrac{\rho_w}{\rho_s}\,(3\,t\,R^2-3\,t^2\,R+t^3)\) There are two more solutions which contains the imaginary component. These solutions are rejected.
One of the common questions in buoyancy is the weight with variable cross section and fix load. For example, a wood wedge of wood with a fix weight/load. The general question is at what the depth of the object (i.e. wedge) will be located. For simplicity, assume that the body is of a solid material.
It is assumed that the volume can be written as a function of the depth. As it was shown in the previous example, the relationship between the depth and the displaced liquid volume of the sphere. Here it is assumed that this relationship can be written as
\[
\label{FixVariableW:d-V}
V_w = f(d,\mbox{other geometrical parameters})
\]
\[
\label{FixVariableW:archimedes1}
\rho_{ll} V_{a}= \rho_{w} V_{w}
\]
\[
\label{FixVariableW:archimedes}
d = f^{-1} \dfrac{\rho_{ll} V_{a}}{ \rho_{w}}
\]
In example 4.26 a general solution was provided. Find the reverse function, \(f^{−1}\) for cone with \(30^∘\) when the tip is in the bottom.
First the function has to built for \(d\) (depth).
\[
\label{woodenCone:gov}
V_{w} = \dfrac{\pi\,d\,\left(\dfrac{d}{\sqrt{3}} \right)^2}{3} = \dfrac{\pi\,d^3}{9}
\]
\[
\label{woodenCone:d}
d = \sqrt[3]{\dfrac{9\,\pi\, \rho_w}{\rho_{ll}\,V_a} }
\]
Fig. 4.37. Schematic of floating bodies.
Template:HideTOC
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.


