6.3: Empirical and Semi-Empirical Models
- Page ID
- 29222
In the period 1949 to present a lot of research has been carried out regarding the head losses of settling slurries. Most researchers developed their equations for the different flow regimes. Models were found for the sliding bed regime, the heterogeneous flow regime and the homogeneous flow regime. Most experiments were carried out measuring the delivered volumetric concentration as a parameter, a few measured the spatial volumetric concentration. Only Yagi et al. (1972) measured both.
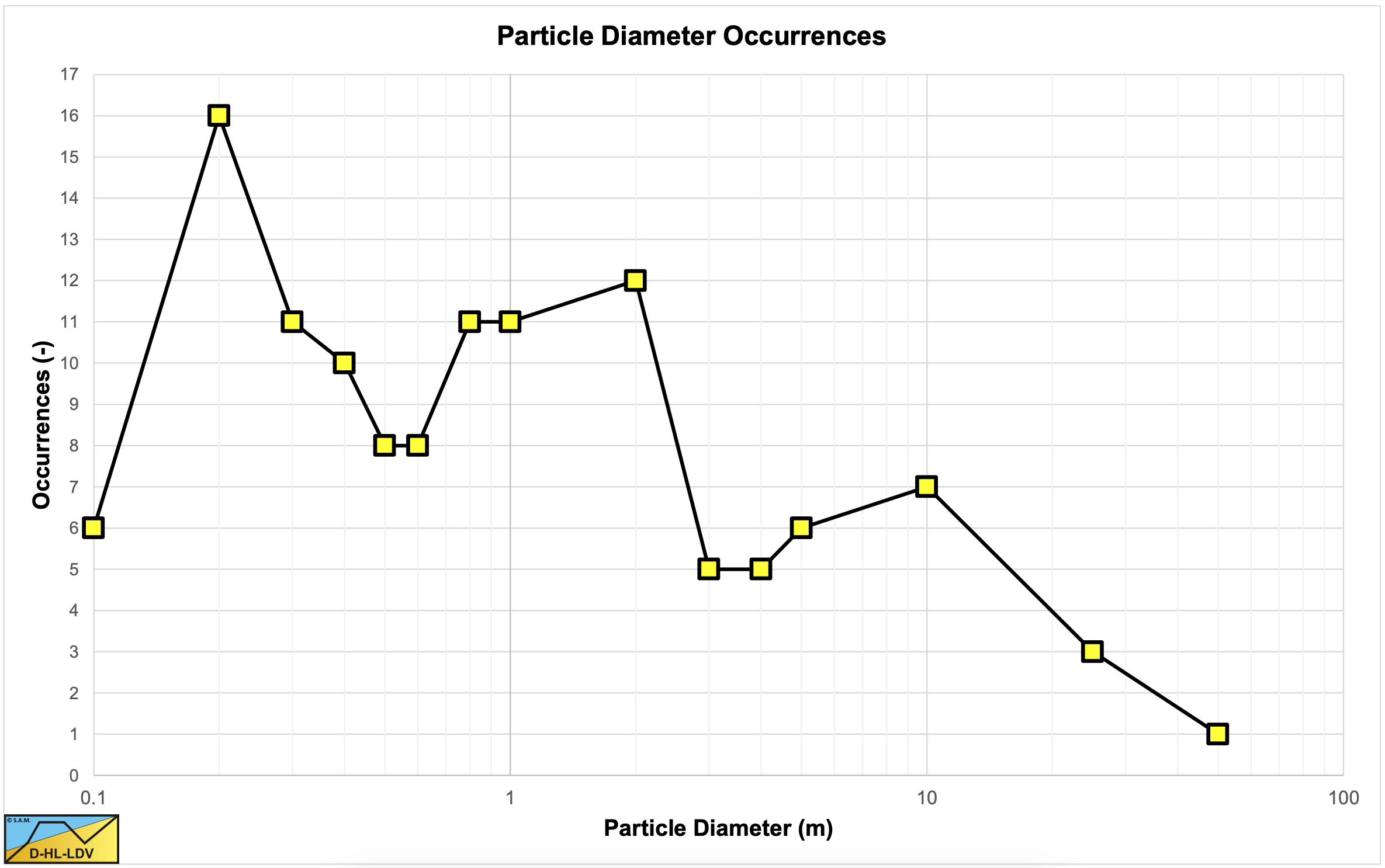
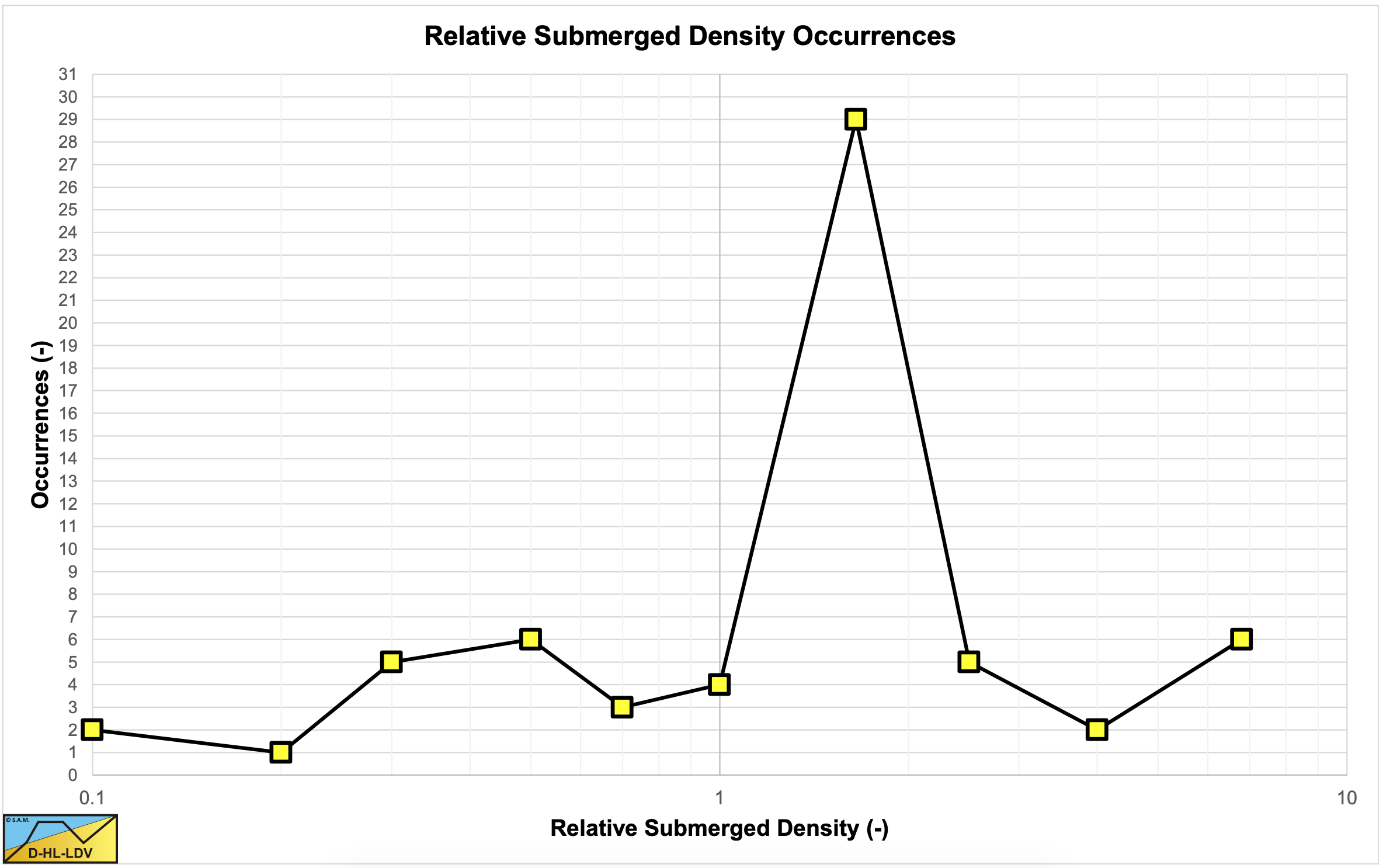
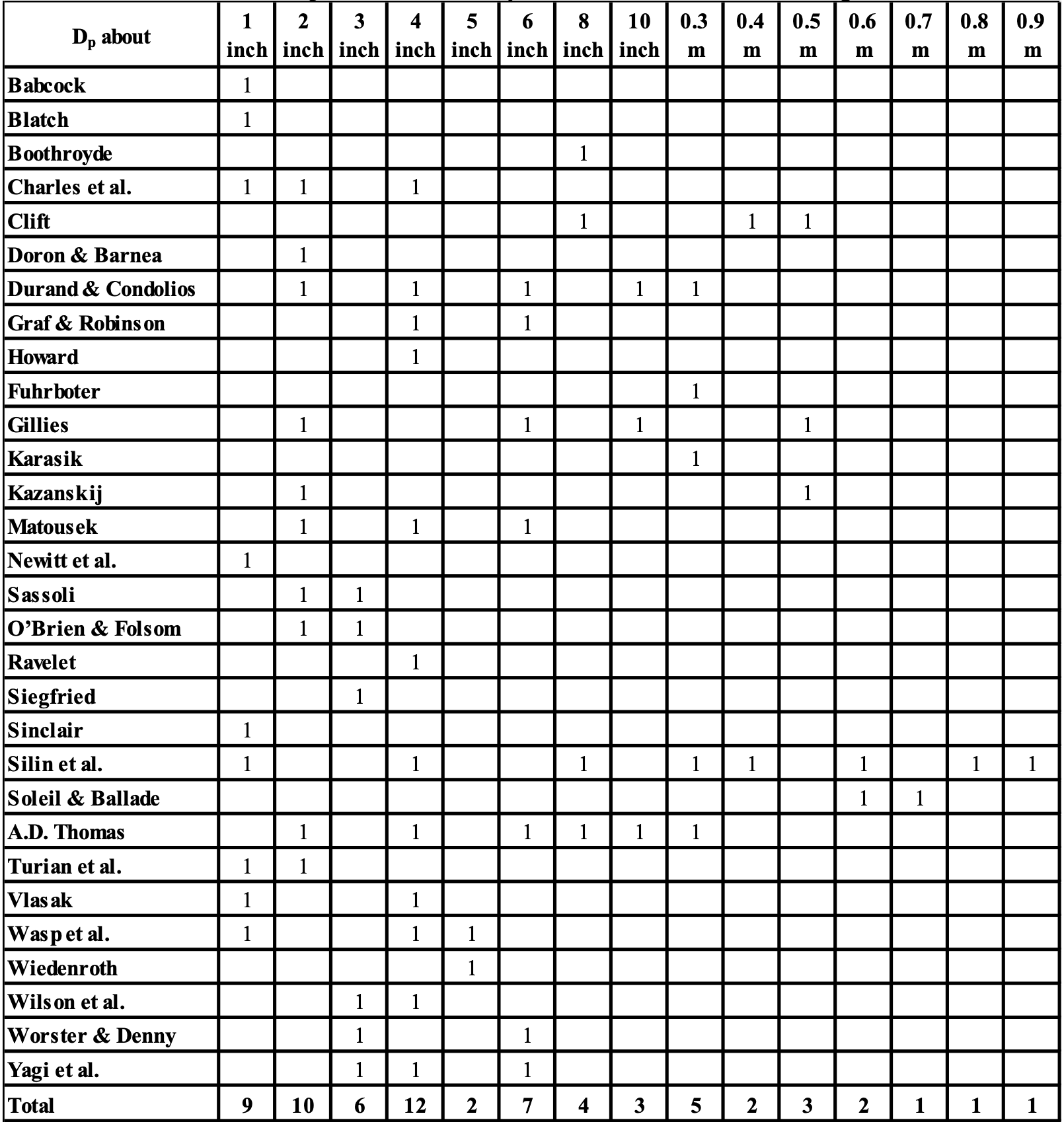
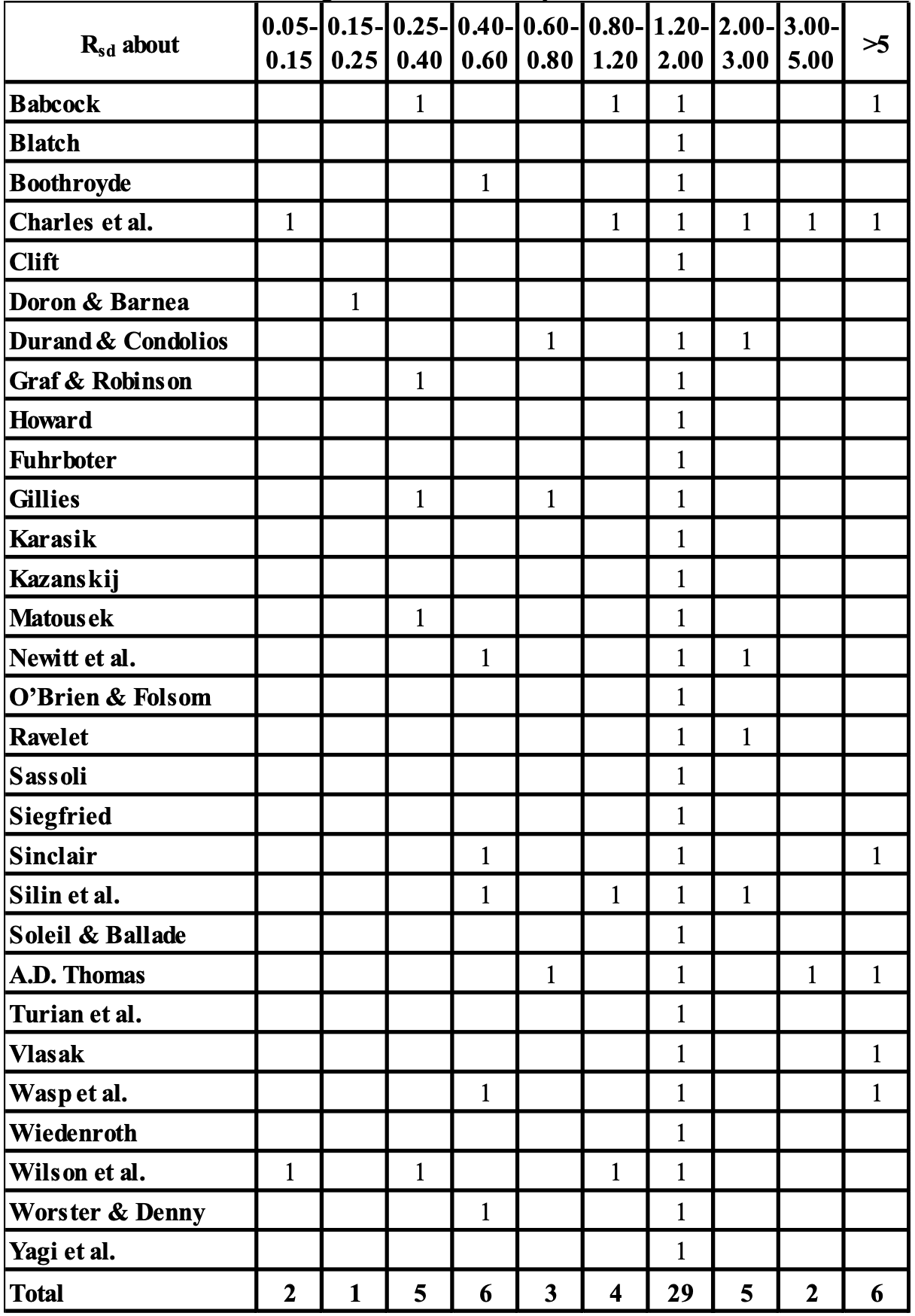
Now it is interesting to see with what pipe diameters, particle diameter and relative submerged densities (or solids densities) the different researchers carried out their experiments. It is impossible to produce a complete list, due to the numerous publications. It is also impossible to have a correct number of occurrences, due to the way of counting. The count is per researcher, not per experiment. So the graphs and tables should be used as an indication.
Figure 6.3-1 and Table 6.3-1 show the number of occurrences of different pipe diameters.
Figure 6.3-2 and Table 6.3-2 show the number of occurrences of different particle diameters.
Figure 6.3-3 and Table 6.3-3 show the number of occurrences of different relative submerged densities.
In the following chapters a number of empirical and semi-empirical models are discussed. The list is far from complete. The models chosen all have some contribution to the development of the DHLLDV Framework.
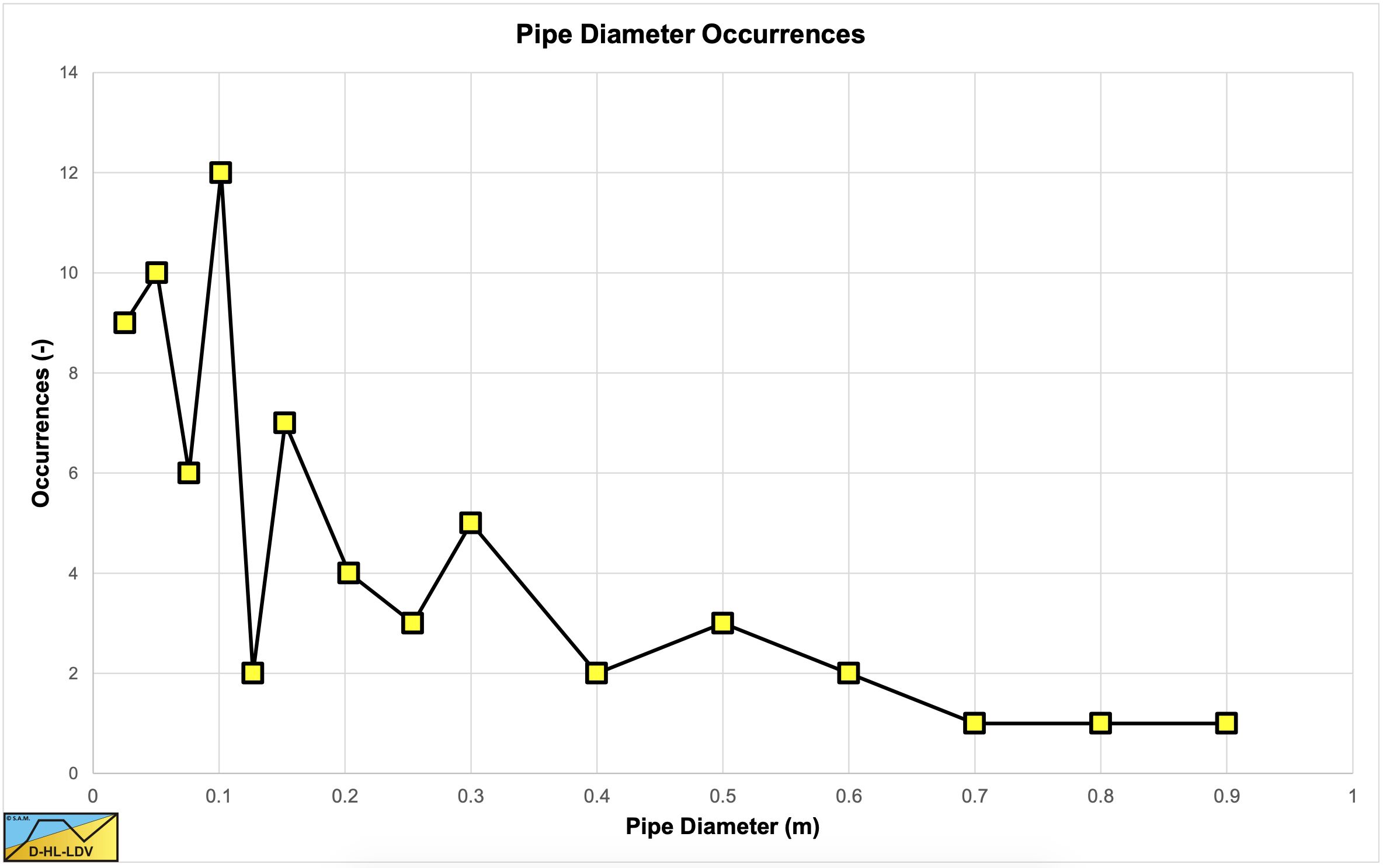
About 60% of the researchers used pipe diameters smaller than or equal to 0.1524 m (6 inch). 82% of the researchers used pipe diameters smaller than or equal to 0.3 m (or 12 inch). Only Silin et al. (1958) carried out experiments in the full range of 0.0254 m up to 0.9 m pipe diameters. These experiments form the basis of the Jufin & Lopatin (1966) model.