5.5: The Influence of Inertial Forces
- Page ID
- 29447
In the previous chapter the shear angle and the cutting forces are given for the influence of the weight only. This will be appropriate for very small cutting velocities, but the question is of course; what is a very low cutting speed.
Analyzing the equations for the influence of the weight (gravity) and the influence of the inertial forces shows a significant difference. The gravitational forces are proportional to the density of the soil ρs, the gravitational constant g, the thickness of the layer cut hi squared and the width of the blade w. The inertial forces are proportional to the density of the soil ρs, the cutting velocity vc squared, the thickness of the layer cut hi and the width of the blade w. This implies that the ratio between these two forces does not only depends on the geometry, but even stronger on the layer thickness hi and the cutting velocity vc. The thicker the layer cut, the higher the influence of gravity and the higher the cutting velocity, the higher the influence of inertia. One cannot say simply the higher the cutting velocity the higher the influence of inertia.
\[\ \text{Gravitation : }\mathrm{F} \propto \rho_{\mathrm{s}} \cdot \mathrm{g} \cdot \mathrm{h}_{\mathrm{i}}^{\mathrm{2}} \cdot \mathrm{w}\tag{5-18}\]
\[\ \text{Inertia :} \quad \mathrm{F} \propto \rho_{\mathrm{s}} \cdot \mathrm{v}_{\mathrm{c}}^{2} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w}\tag{5-19}\]
The contribution of the inertial forces is determined by the following dimensionless parameter:
\[\ \lambda_{\mathrm{i}}=\frac{\mathrm{v}_{\mathrm{c}}^{2}}{\mathrm{g} \cdot \mathrm{h}_{\mathrm{i}}}\tag{5-20}\]
In dredging a layer thickness of the magnitude of centimeters is common, while for a bulldozer a layer thickness of a magnitude of a meter is not strange. At the same cutting velocity, the relative influence of inertial forces will differ between dredging applications and the operation of bulldozers. If inertial forces dominate the cutting process, the cutting forces can be expressed as:
\[\ \begin{array}{left} \mathrm{F}_{\mathrm{h}}=\rho_{\mathrm{s}} \cdot \mathrm{v}_{\mathrm{c}}^{\mathrm{2}} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w} \cdot \lambda_{\mathrm{H I}}\\
\text{With :} \quad \lambda_{\mathrm{H I}}=\frac{\sin (\alpha)}{\sin (\alpha+\beta)} \cdot \frac{\cos (\varphi)}{\sin (\alpha+\beta+\delta+\varphi)} \cdot \sin (\alpha+\delta)\end{array}\tag{5-21}\]
\[\ \begin{array}{left}\mathrm{F}_{v}=\rho_{\mathrm{s}} \cdot \mathrm{v}_{\mathrm{c}}^{\mathrm{2}} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w} \cdot \lambda_{\mathrm{V I}}\\
\text{With : }\quad \lambda_{\mathrm{V I}}=\frac{\sin (\alpha)}{\sin (\alpha+\beta)} \cdot \frac{\cos (\varphi)}{\sin (\alpha+\beta+\delta+\varphi)} \cdot \cos (\alpha+\delta)\end{array}\tag{5-22}\]
These equations are derived from equations (5-6), (5-7), (5-9) and (5-10). The shear angle β can be derived analytically for the inertial forces, giving:
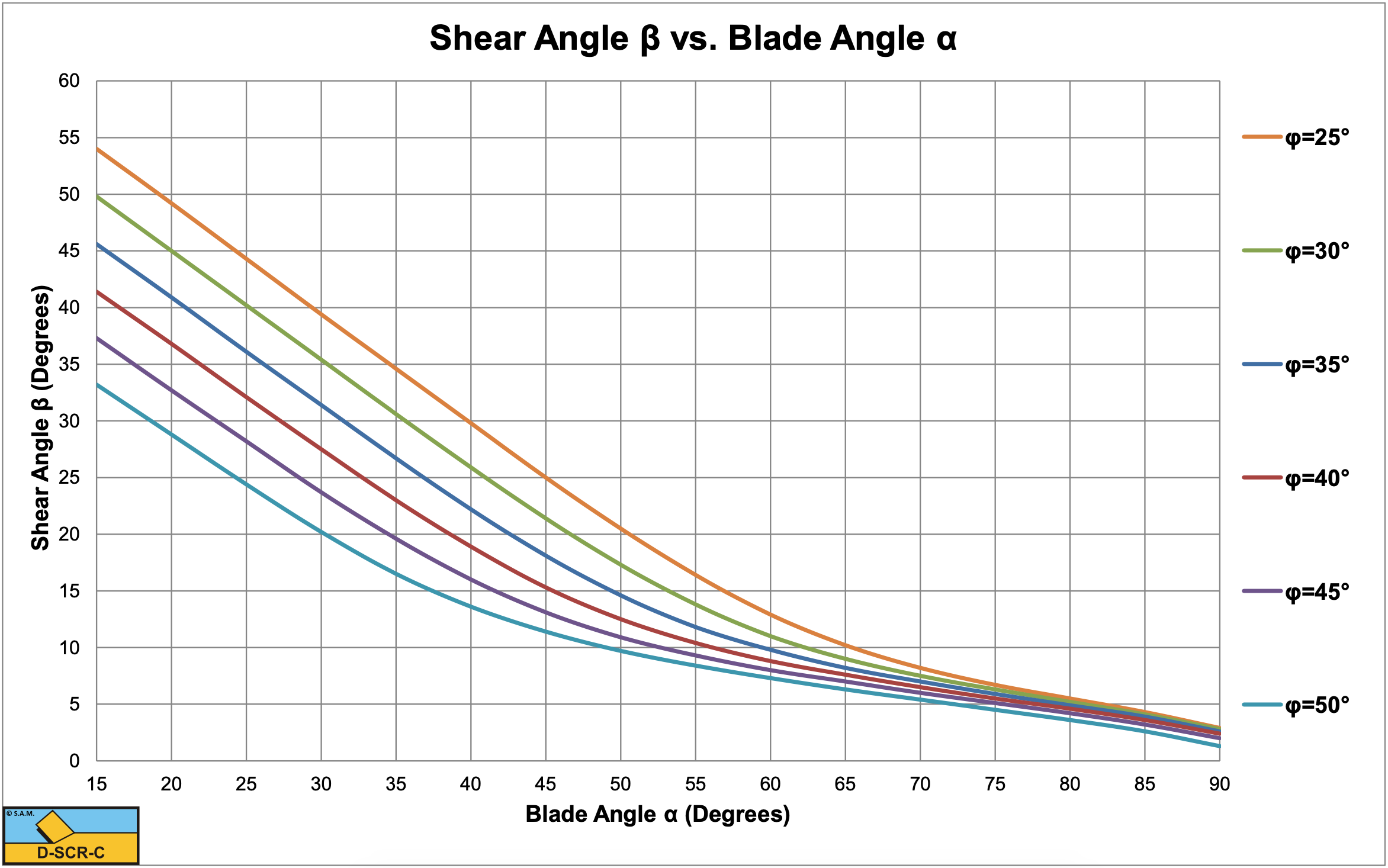
\[\ \beta=\frac{\pi}{2}-\frac{2 \cdot \alpha+\delta+\varphi}{2}\tag{5-23}\]
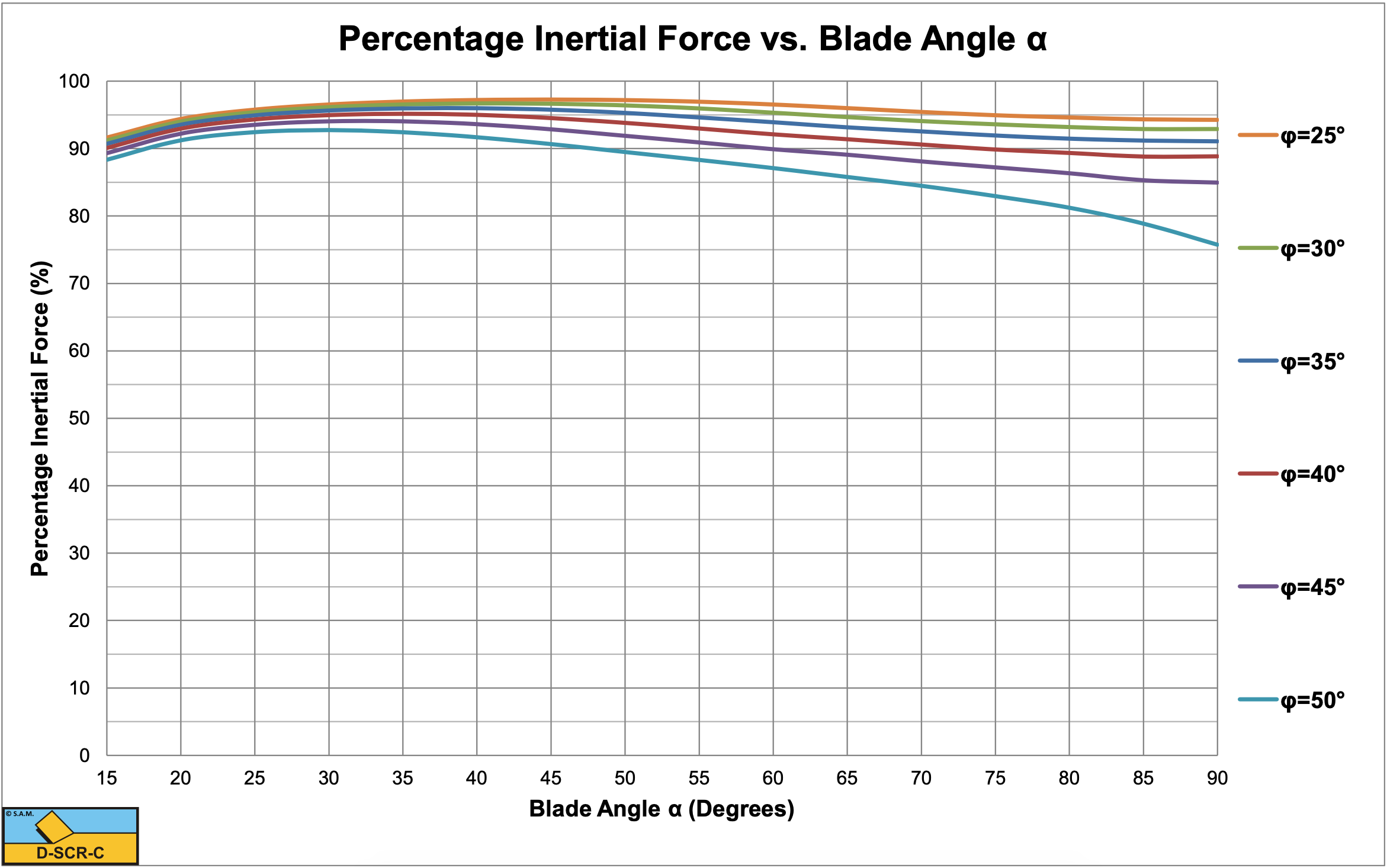
Figure 5-13 shows the percentage of the contribution of the inertial forces to the horizontal cutting force for a layer thickness hi of 1.0 m at a cutting velocity of 0.5 m/sec, giving λi=0.025. Figure 5-14 shows the percentage of the contribution of the inertial forces to the horizontal cutting force for a layer thickness hi of 0.1 m at a cutting velocity of 15.7 m/sec, giving λi=250.
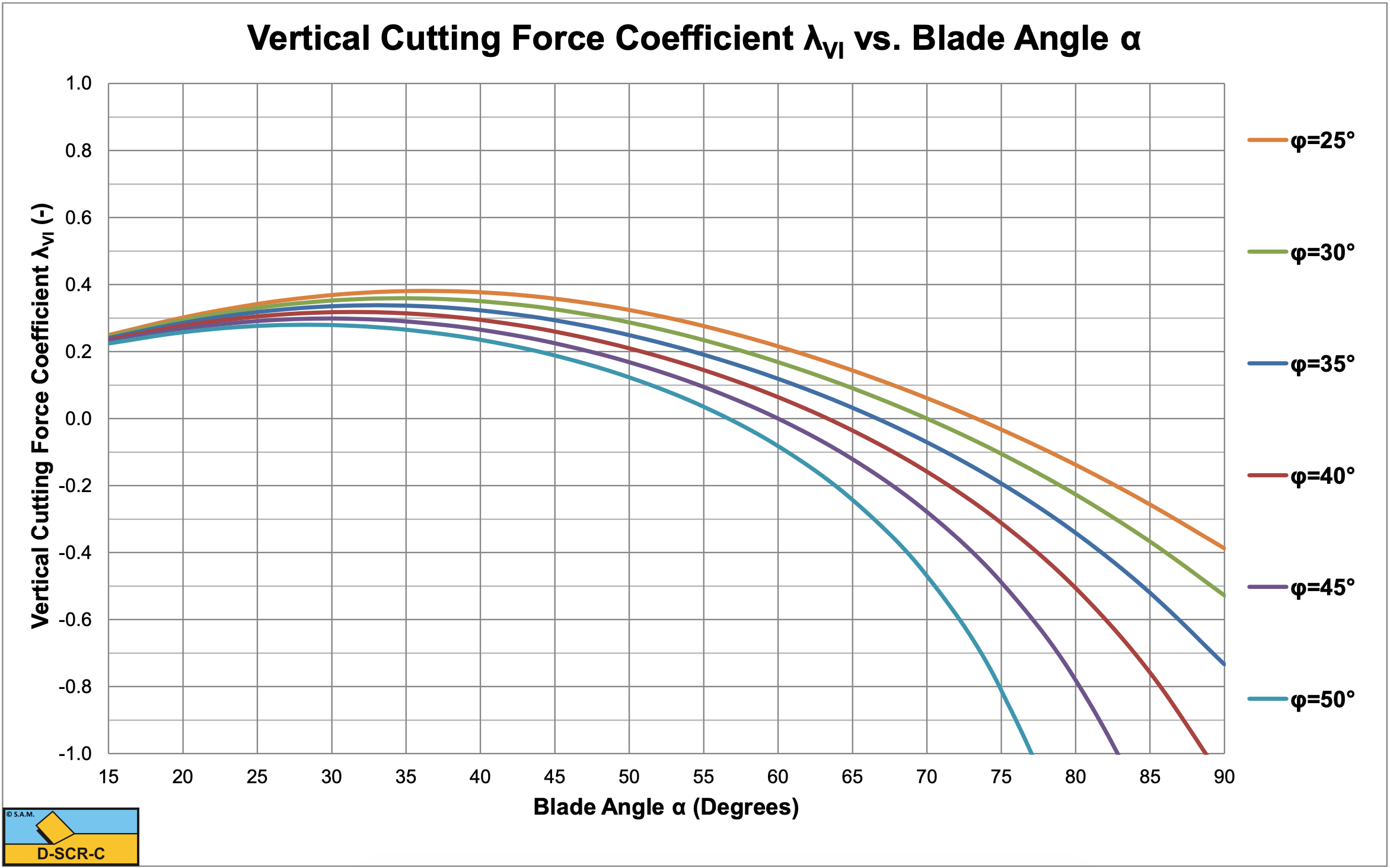
Table 5-1 shows the inertial effect for the dimensionless inertial effect parameter λi ranging from 0.025 to 250. The percentage contribution of the inertial effect on the horizontal force is given as well as the shear angle, both horizontal and vertical cutting force coefficients based on equations (5-21) and (5-22) and both horizontal and vertical cutting force coefficients based on equations (5-13) and (5-14) for the case where the blade height hb equals the layer thickness hi. The table shows that the inertial effect can be neglected at very small values of the dimensionless inertial effect parameter λi, while at large values the gravitational effect can be neglected. The shear angle β decreases with an increasing dimensionless inertial effect parameter λi. Since the inertial forces are not influenced by the blade height hb, the cutting forces are not dependent on the blade height at high cutting velocities. At low cutting velocities there will be an effect of the blade height.
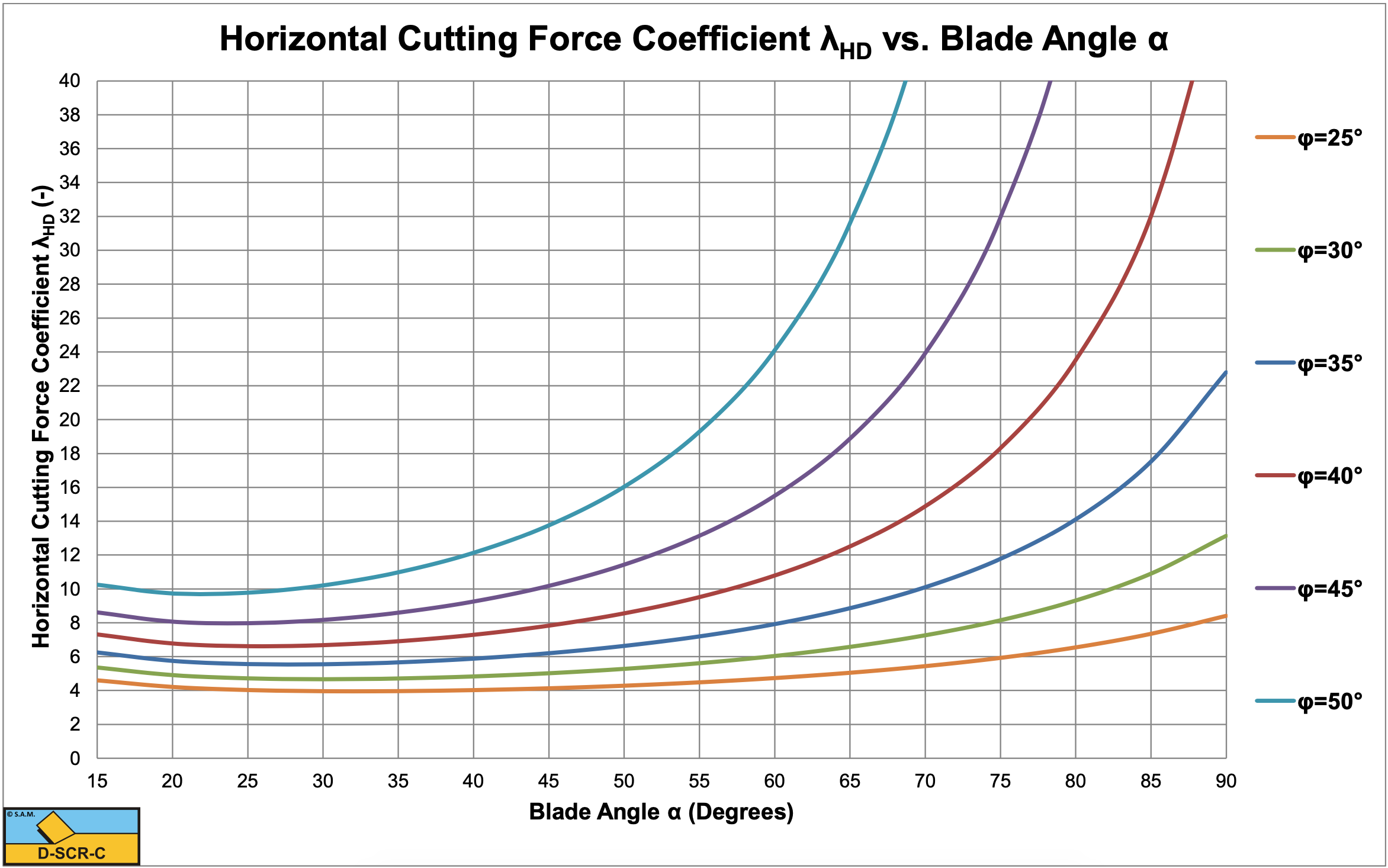
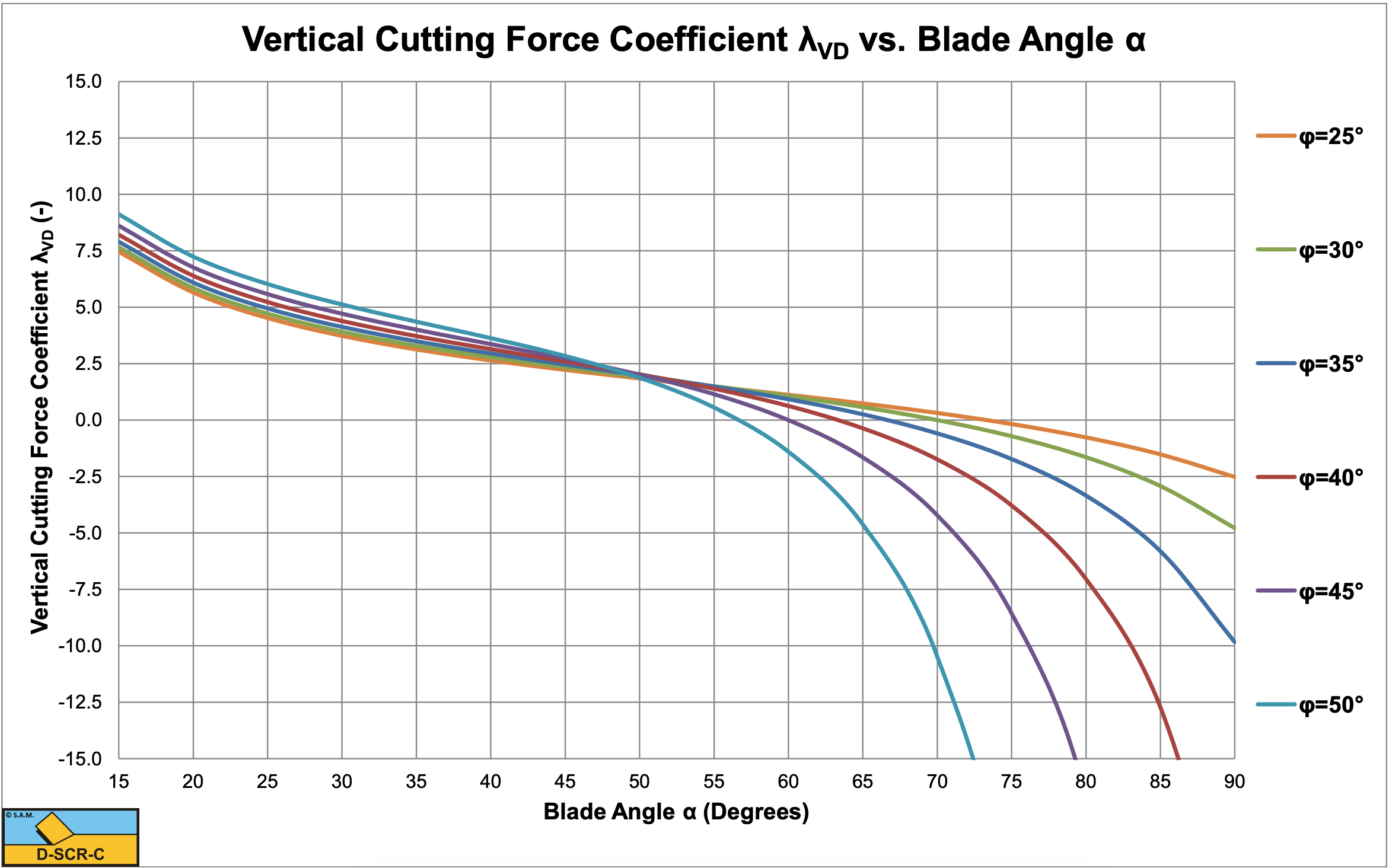
The contribution of the inertial effect only depends on the dimensionless inertial effect parameter λi and not on the cutting velocity or layer thickness individually. The dimensionless inertial effect parameter λi in fact is a Froude number of the cutting process. Figure 5-15, Figure 5-16 and Figure 5-17 show the shear angle and both horizontal and vertical cutting force coefficients at very high values of the dimensionless inertial effect parameter λi (λi=250). The shear angles are considerably smaller than in the case where inertial forces can be neglected. Also in the case where the inertial forces dominate, the cutting forces become very high at large blade angles (close to 90°). Nature will find an alternative cutting mechanism in this case which has been identified as the wedge mechanism. At which blade angle the wedge mechanism will start to occur depends on the internal and external friction angles, but up to a blade angle of 60° the model as described here can be applied. See Chapter 11: A Wedge in Dry SandCutting for detailed information on the wedge mechanism.

|
λi |
% |
β |
λHI |
λVI |
λHD |
λHV |
|
0.025 |
0.74 |
31.6 |
187.68 |
27.49 |
4.78 |
0.70 |
|
0.250 |
6.65 |
30.8 |
20.26 |
2.97 |
5.09 |
0.75 |
|
2.500 |
37.69 |
26.0 |
3.12 |
0.46 |
7.95 |
1.16 |
|
25.00 |
78.98 |
16.9 |
1.25 |
0.18 |
31.40 |
4.60 |
|
250.0 |
94.98 |
9.6 |
0.96 |
0.14 |
245.36 |
35.94 |


