8.5: Determining the Angle β

Last updated
Save as PDF

Page ID: 29468

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

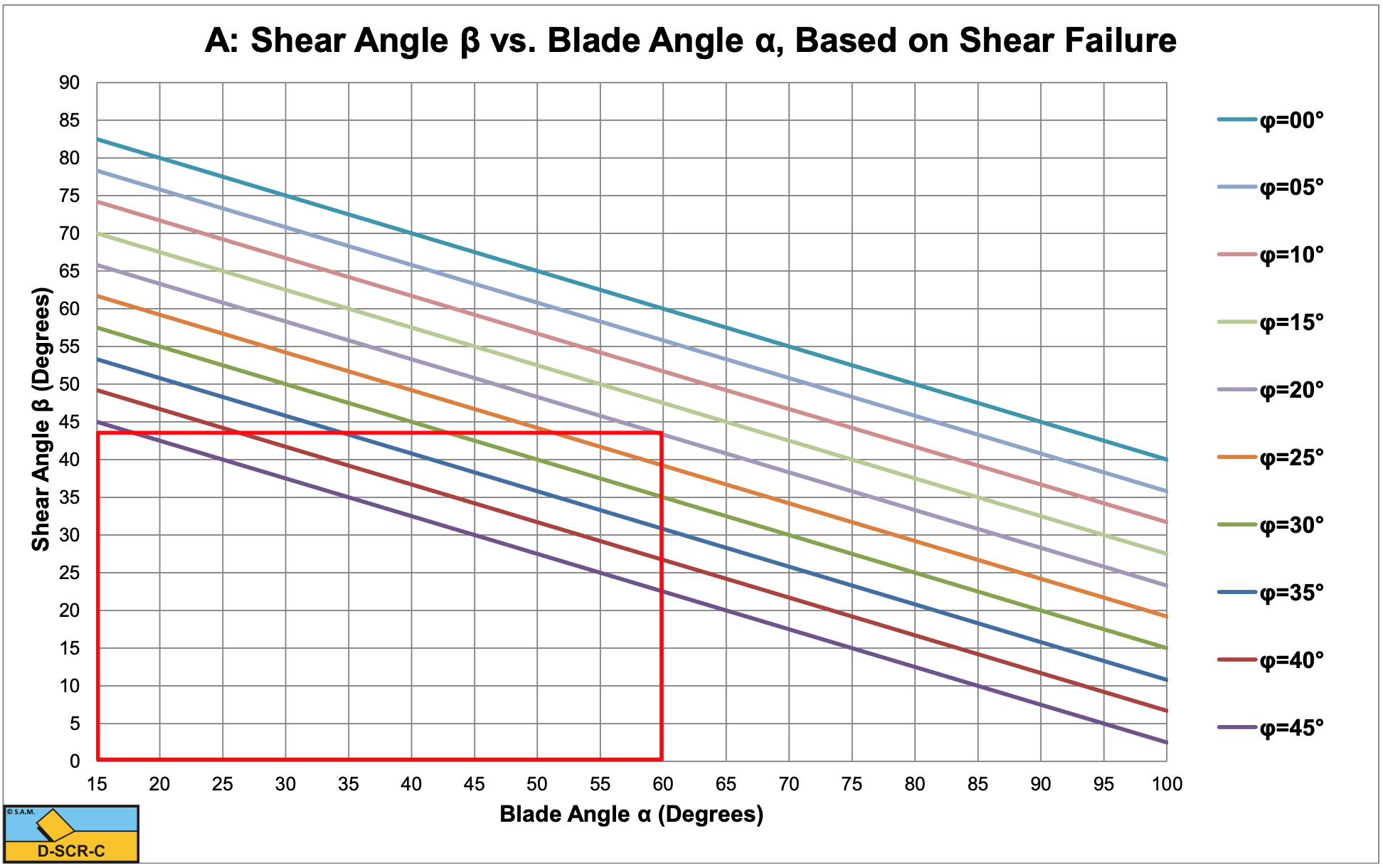
To determine the shear angle β where the horizontal force F_h is at the minimum, the denominator of equation (8-105) has to be at a maximum. This will occur when the derivative of F_h with respect to β equals 0 and the second derivative is negative.

\[\ \frac{\partial \sin (\alpha+\beta+\delta+\varphi) \cdot \sin (\beta)}{\partial \beta}=\sin (\alpha+2 \cdot \beta+\delta+\varphi)=0\tag{8-107}\]

\[\ \beta=\frac{\pi}{2}-\frac{\alpha+\delta+\varphi}{2}\tag{8-108}\]

This gives for the cutting forces:

\[\ \mathrm{F_{h}=\frac{2 \cdot c \cdot h_{i} \cdot w \cdot \cos (\varphi) \cdot \sin (\alpha+\delta)}{1+\cos (\alpha+\delta+\varphi)}=\lambda_{H F} \cdot c \cdot h_{i} \cdot w}\tag{8-109}\]

\[\ \mathrm{F}_{v}=\mathrm{\frac{2 \cdot c \cdot h_{i} \cdot w \cdot \cos (\varphi) \cdot \cos (\alpha+\delta)}{1+\cos (\alpha+\delta+\varphi)}=\lambda_{V F} \cdot c \cdot h_{i} \cdot w}\tag{8-110}\]

Equations (8-109) and (8-110) are basically the same as the equations found by Merchant (1944), (1945A) and (1945B). The normal force N₁ and the normal stress σ_N1 on the shear plane are now (with λ_s=1):

\[\ \begin{array}{left}\mathrm{N}_{1}=\frac{-\mathrm{C} \cdot \cos (\alpha+\beta+\delta)}{\sin (\alpha+\beta+\delta+\varphi)} \cdot \cos (\varphi)\\
\sigma_{\mathrm{N} 1}=\frac{-\mathrm{c} \cdot \cos (\alpha+\beta+\delta)}{\sin (\alpha+\beta+\delta+\varphi)} \cdot \cos (\varphi)\end{array}\tag{8-111}\]

The normal force N₂ and the normal stress σ_N2on the blade are now:

\[\ \begin{array}{left}\mathrm{N}_{2}&=\frac{\mathrm{C} \cdot \cos (\varphi)}{\sin (\alpha+\beta+\delta+\varphi)} \cdot \cos (\delta)\\
\sigma_{\mathrm{N} 2}&=\mathrm{c} \cdot \frac{\mathrm{h}_{\mathrm{i}} \cdot \sin (\alpha)}{\mathrm{h}_{\mathrm{b}} \cdot \sin (\beta)} \cdot \frac{\cos (\varphi)}{\sin (\alpha+\beta+\delta+\varphi)} \cdot \cos (\delta)\end{array}\tag{8-112}\]

Equations (8-111) and (8-112) show that the normal force on the shear plane tends to be negative, unless the sum of the angles α+β+δ is greater than 90°. With the use of equation (8-108) the following condition is found:

\[\ \begin{array}{left}\alpha+\beta+\delta=\alpha+\delta+\left(\frac{\pi}{2}-\frac{\alpha+\delta+\varphi}{2}\right)=\frac{\pi}{2}+\frac{\alpha+\delta-\varphi}{2}>\frac{\pi}{2}\\
\text{so: }\frac{\alpha+\delta-\varphi}{2}>0\end{array}\tag{8-113}\]

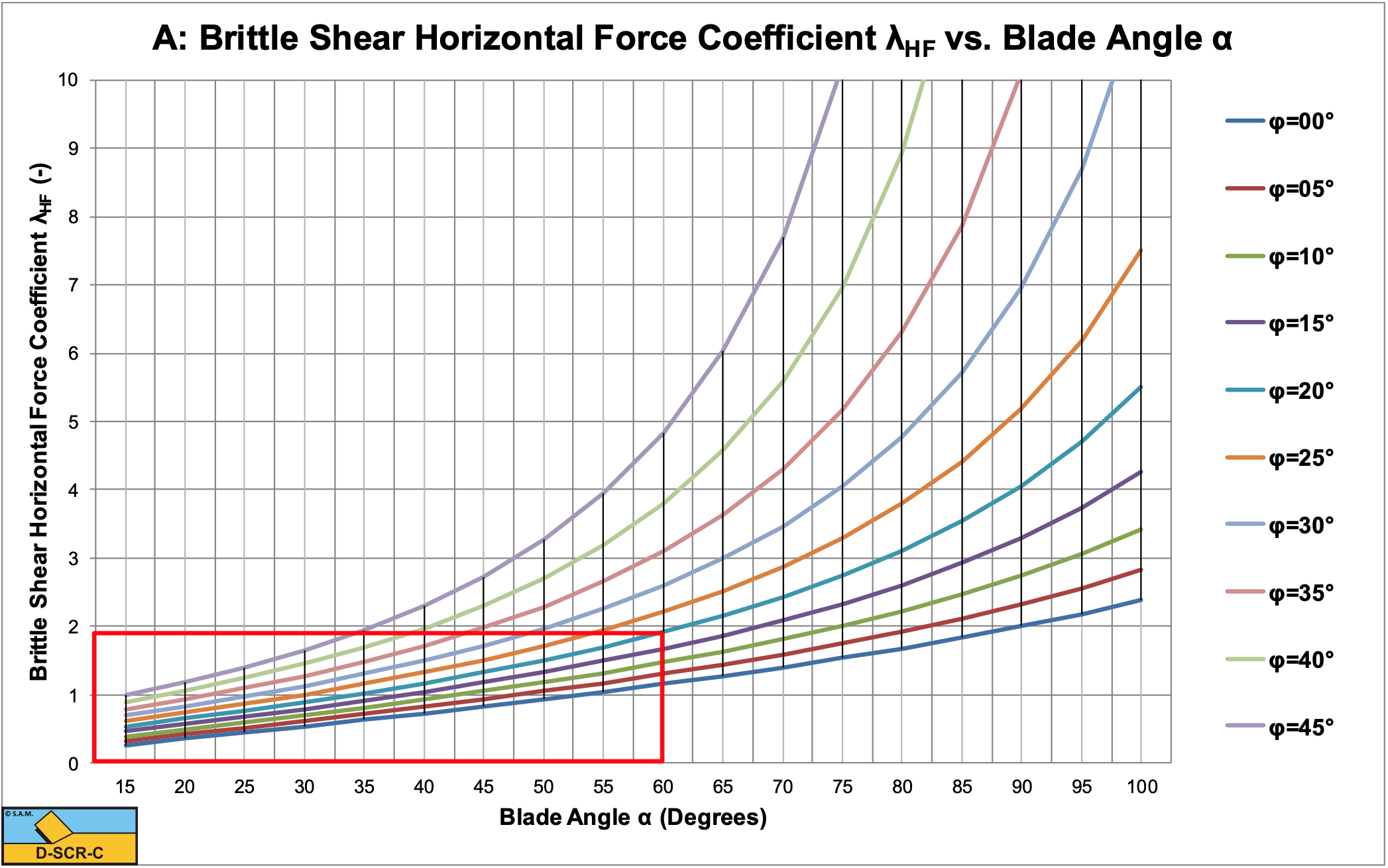
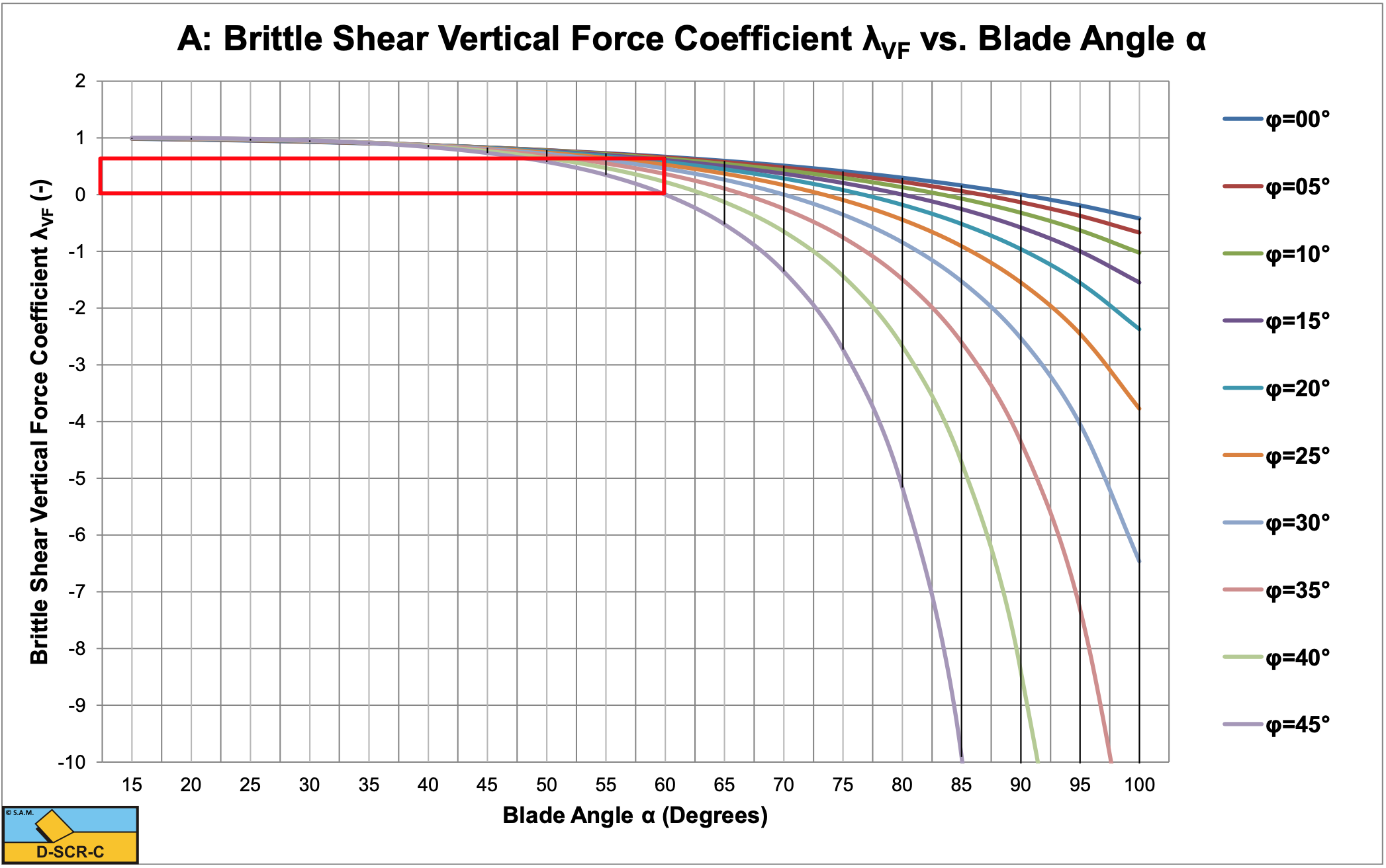
Because for normal blade angles this condition is always valid, the normal force is always positive. Figure 8-31 and Figure 8-32 show the coefficients λ_HF and λ_VFfor the horizontal and vertical forces F_h and F_v according to equations (8-109) and (8-110) as a function of the blade angle α and the internal friction angle φ, where the external friction angle δ is assumed to be 2/3·φ. A positive coefficient λ_VF for the vertical force means that the vertical force F_vis downwards directed.

Screen Shot 2020-08-22 at 11.59.57 PM.png — Figure 8-30: The shear angle β **as a function of the blade angle** α **and the angle of internal friction** φ.

Based on equation (8-97) and (8-109) the specific energy E_sp can be determined according to:

\[\ \mathrm{E}_{\mathrm{sp}}=\frac{\mathrm{P}_{\mathrm{c}}}{\mathrm{Q}}=\frac{\mathrm{F}_{\mathrm{h}} \cdot \mathrm{v}_{\mathrm{c}}}{\mathrm{h}_{\mathrm{i}} \cdot \mathrm{w} \cdot \mathrm{v}_{\mathrm{c}}}=\frac{\mathrm{F}_{\mathrm{h}}}{\mathrm{h}_{\mathrm{i}} \cdot \mathrm{w}}=\lambda_{\mathrm{H F}} \cdot \mathrm{c}\tag{8-114}\]

The cohesive shear strength c is a function of the Unconfined Compressive Strength UCS and the angle of internal friction φ according to (see Figure 8-36):

\[\ \mathrm{c=\frac{U C S}{2} \cdot\left(\frac{1-\sin (\varphi)}{\cos (\varphi)}\right)}\tag{8-115}\]

This gives for the specific energy E_sp:

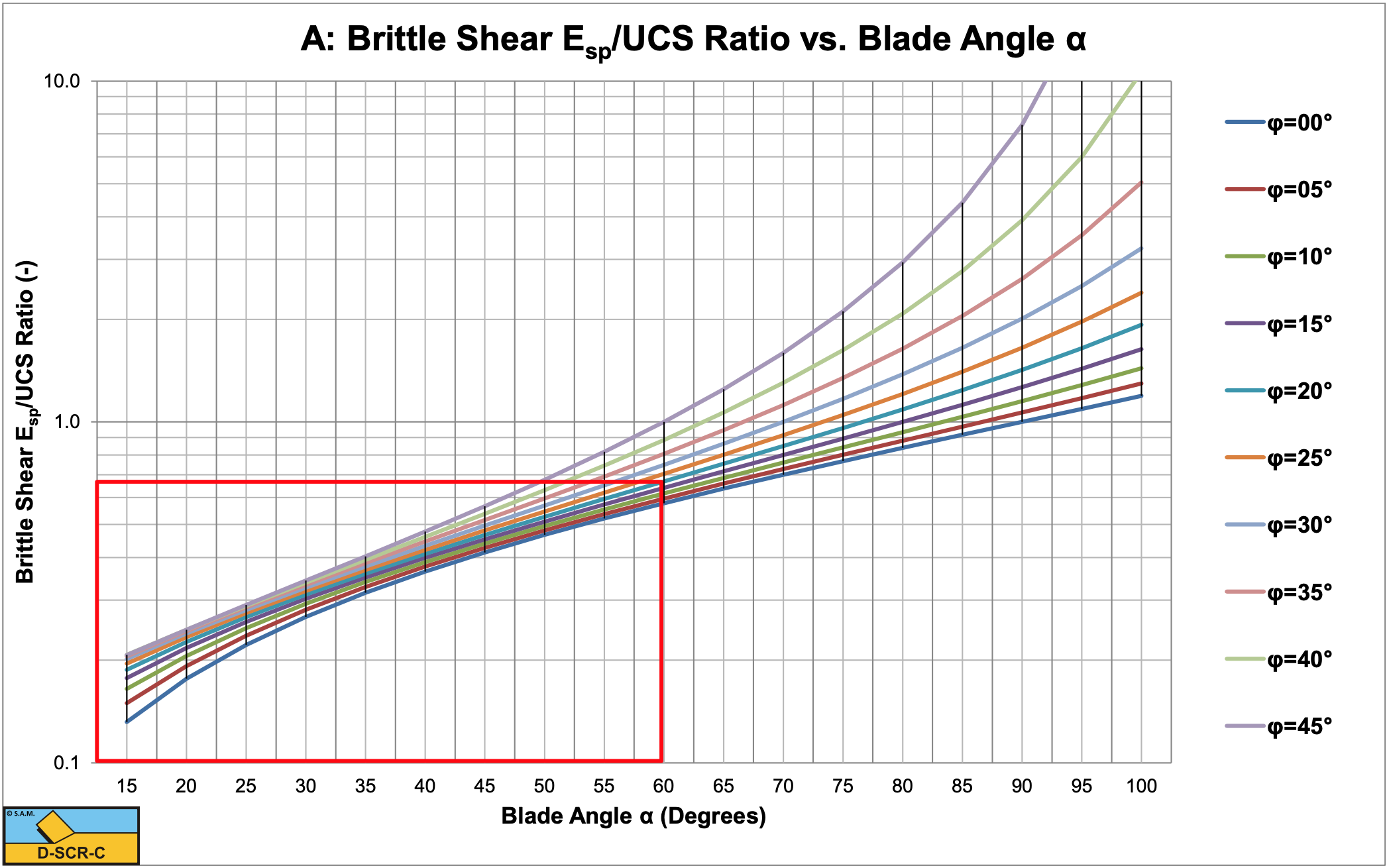
\[\ \mathrm{E}_{\mathrm{sp}}=\lambda_{\mathrm{HF}} \cdot \mathrm{c}=\lambda_{\mathrm{HF}} \cdot \frac{\mathrm{U} \mathrm{C S}}{2} \cdot\left(\frac{1-\sin (\varphi)}{\cos (\varphi)}\right)\tag{8-116}\]

Figure 8-33 shows the specific energy E_sp to UCS ratio. In Figure 8-30, Figure 8-31, Figure 8-32 and Figure 8-33 an example is given for an α=60^o blade and an internal friction angle of φ=20^o.
It should be noted again that the forces and the specific energy are based on peak values. For the average this should be multiplied with a factor between 0.5 and 1.0, but closer to 0.5.

Screen Shot 2020-08-23 at 12.10.41 AM.png — Figure 8-31: The brittle (shear failure) horizontal force coefficient λ_HF.

Screen Shot 2020-08-23 at 12.11.42 AM.png — Figure 8-32: The brittle (shear failure) vertical force coefficient λ_VF.

If the forces become to high another mechanism will occur, for example the wedge mechanism.

Screen Shot 2020-08-23 at 12.12.27 AM.png — Figure 8-33: The specific energy E_sp **to UCS ratio.**