12.9: The Dynamic Wedge

Last updated
Save as PDF

Page ID: 35014

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

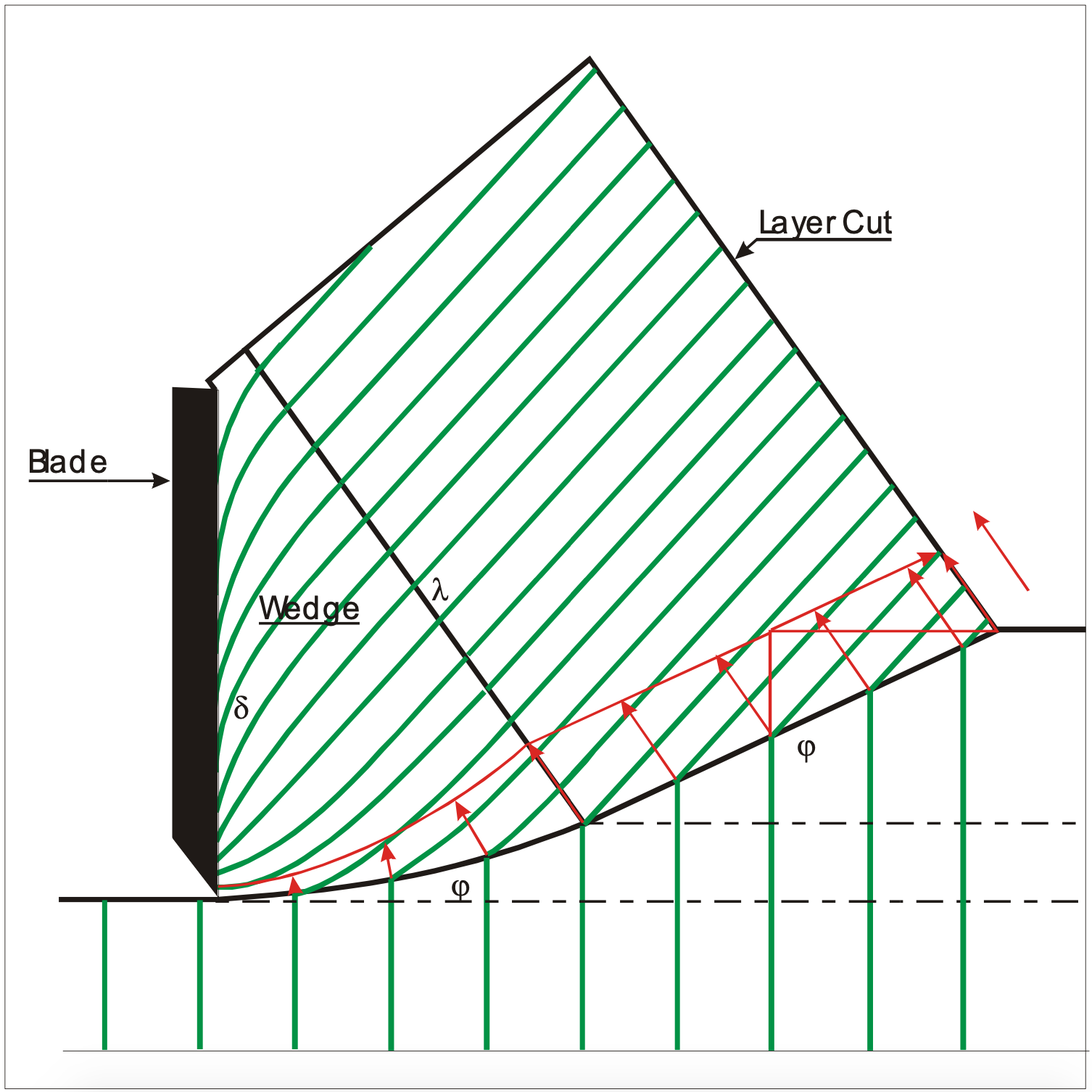
As discussed in the above paragraphs, the new research has led to the insight that the wedge in front of the blade is not static but dynamic. The aim of the new research was to get a good understanding of the mechanisms involved in the cutting at large cutting angles. To achieve this, vertical bars of about 10 cm deep with colored sand grains were inserted in the sand as is shown in Figure 12-39. When these bars are cut they will be deformed. If the wedge in front of the blade is a static wedge, meaning that the grains in the wedge have no velocity relative to the blade, then the colored grains from the bars will not enter the wedge. If however the colored grains enter the wedge, this means that the grains in the wedge move with respect to the blade. The research has shown that the colored grains have entered the wedge according to Figure 12-39. In the layer cut, the colored grains show a straight line, which is obvious, because of the velocity distribution in the layer cut. In fact the layer cut moves as a rigid body. In the wedge the colored grains show a curved line. Because of the velocity distribution in the wedge, the grains near the blade move much slower than the grains in the layer cut. Although Figure 12-39 shows a line between the layer cut and the wedge, in reality there does not exist a clear boundary between these two surfaces. The grains on both sides of the drawn boundary line will have (almost) the same velocity, resulting in an internal friction angle λ, which is not fully mobilized. The external friction angle on the blade however is fully mobilized. This contradicts the findings of Miedema et al. (2002A), from previous research. The value of this internal friction angle is between 0<λ<φ. Further research will have to show the value of λ.

Screen Shot 2020-08-25 at 9.20.58 PM.png — Figure 12-39: The dynamic wedge.