1.3: Equilibrium Structures, Support Reactions, Determinacy and Stability of Beams and Frames
- Page ID
- 17609
Equilibrium Structures, Support Reactions, Determinacy and Stability of Beams and Frames
Engineering structures must remain in equilibrium both externally and internally when subjected to a system of forces. The equilibrium requirements for structures in two and three dimensions are stated below.
3.1.1 Equilibrium in Two Dimensions
For a structure subjected to a system of forces and couples which are lying in the xy plane to remain at rest, it must satisfy the following three equilibrium conditions:

The above three conditions are commonly referred to as the equations of equilibrium for planar structures. ∑ Fx and ∑ Fy are the summation of the x and y components of all the forces acting on the structure, and ∑ Mz is the summation of the couple moments and the moments of all the forces about an axis z, perpendicular to the plane xy of the action of the forces.
3.1.2 Equilibrium in Three Dimensions
A structure in three dimensions, that is, in a space, must satisfy the following six requirements to remain in equilibrium when acted upon by external forces:

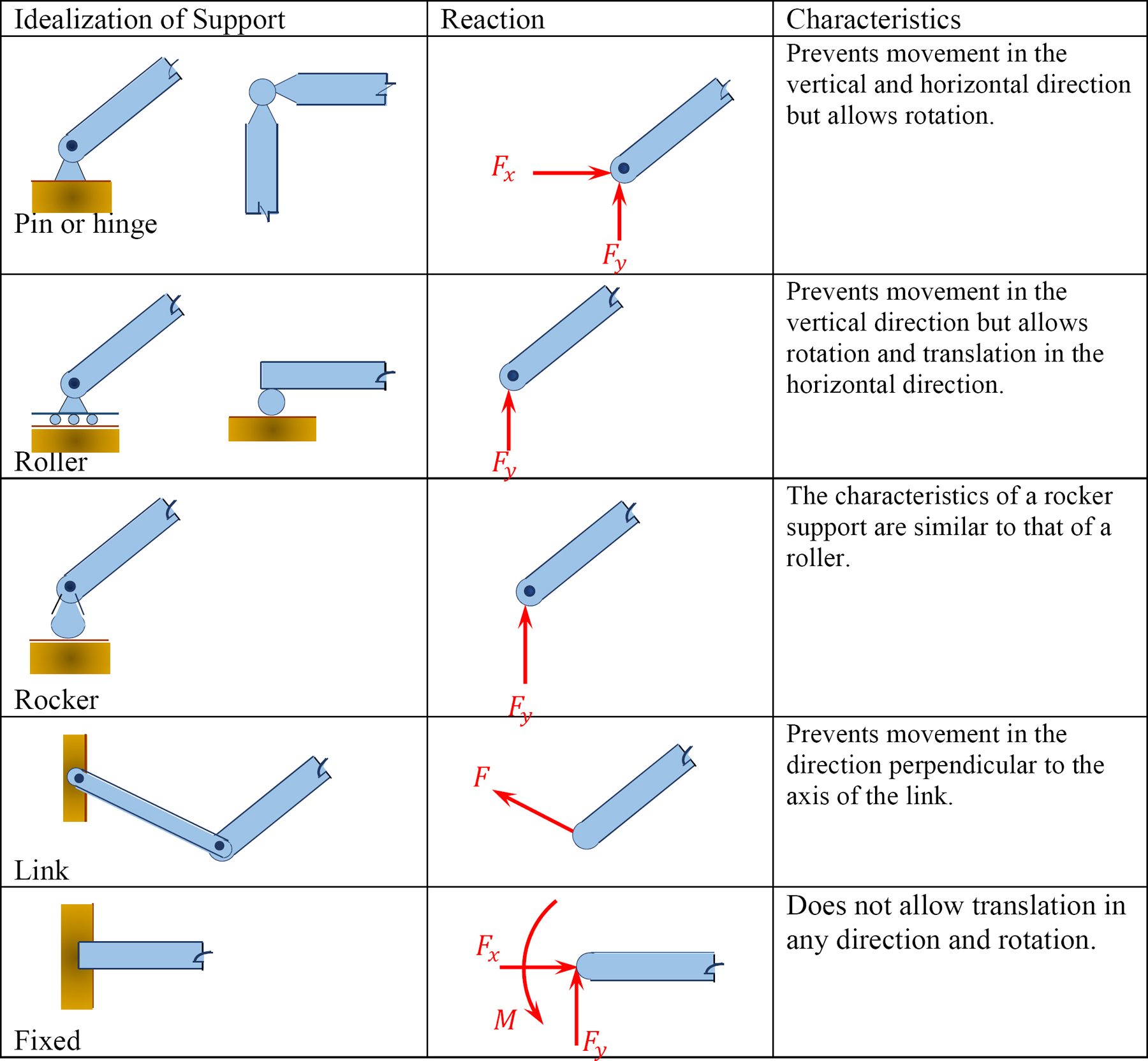
3.2 Types of Supports and Their Characteristics
The type of support provided for a structure is important in ensuring its stability. Supports connect the member to the ground or to some other parts of the structure. It is assumed that the student is already familiar with several types of supports for rigid bodies, as this was introduced in the statics course. However, the characteristics of some of the supports are described below and shown in Table 3.1.
3.2.1 Pin or Hinge Support
A pin support allows rotation about any axis but prevents movement in the horizontal and vertical directions. Its idealized representation and reactions are shown in Table 3.1.
3.2.2 Roller Support
A roller support allows rotation about any axis and translation (horizontal movement) in any direction parallel to the surface on which it rests. It restrains the structure from movement in a vertical direction. The idealized representation of a roller and its reaction are also shown in Table 3.1.
3.2.3 Rocker Support
The characteristics of a rocker support are like those of the roller support. Its idealized form is depicted in Table 3.1.
3.2.4 Link
A link has two hinges, one at each end. It permits movement in all direction, except in a direction parallel to its longitudinal axis, which passes through the two hinges. In other words, the reaction force of a link is in the direction of the link, along its longitudinal axis.
3.2.5 Fixed Support
A fixed support offers a constraint against rotation in any direction, and it prevents movement in both horizontal and vertical directions.
3.3 Determinacy and Stability of Beams and Frames
Prior to the choice of an analytical method, it is important to establish the determinacy and stability of a structure. A determinate structure is one whose unknown external reaction or internal members can be determined using only the conditions of equilibrium. An indeterminate structure is one whose unknown forces cannot be determined by the conditions of static equilibrium alone and will require, in addition, a consideration of the compatibility conditions of different parts of the structure for its complete analysis. Furthermore, structures must be stable to be able to serve their desirable functions. A structure is considered stable if it maintains its geometrical shape when subjected to external forces.
3.3.1 Formulations for Stability and Determinacy of Beams and Frames
The conditions of determinacy, indeterminacy, and instability of beams and frames can be stated as follows:

where
r = number of support reactions.
C = equations of condition (two equations for one internal roller and one equation for each internal pin).
m = number of members.
j = number of joints.
Table 3.1. Types of supports.
3.3.2 Alternative Formulation for Determinacy and Stability of Beams and Frames

where
r = number of support reactions.
Fi = number of reaction forces transmitted by an internal hinge or internal roller.
m = number of members.
Example 3.1
Classify the beams shown in Figure 3.1 through Figure 3.5 as stable, determinate, or indeterminate, and state the degree of indeterminacy where necessary.

Solution
First, draw the free-body diagram of each beam. To determine the classification, apply equation 3.3 or equation 3.4.
Using equation 3.3, r = 7, m = 2, c = 0, j = 3. Applying the equation leads to 3(2) + 7 > 3(3) + 0, or 13 > 9. Therefore, the beam is statically indeterminate to the 4°.
Using equation 3.4, r = 7, m = 1, Fi = 0. Applying the equation leads to 7 + 0 > (3)(1), or 7 > 3. Therefore, the beam is statically indeterminate to the 4°.
Note: When using equation 3.3, the portions on either side of the interior support are counted as separate members.

Solution
Using equation 3.3, r = 6, m = 3, c = 0, j = 4. Applying the equation leads to 3(3) + 6 > 3(4) + 0, or 15 > 12. Therefore, the beam is statically indeterminate to the 3°.
Using equation 3.4, r = 6, m = 1, Fi = 0. Applying the equation leads to 6 + 0 > (3)(1), or 6 > 3. Therefore, the beam is statically indeterminate to the 3°.

Solution
Using equation 3.3, r = 5, m = 3, c = 1, j = 4. Applying the equation leads to 3(3) + 5 > 3(4) + 1, or 14 > 13. Therefore, the beam is statically indeterminate to the 1°.
Using equation 3.4, r = 5, m = 2, Fi = 2. Applying the equation leads to 5 + 2 > 3(2), or 7 > 6. Therefore, the beam is statically indeterminate to the 1°.

Solution
Using equation 3.3, r = 5, m = 4, c = 1, j = 5. Applying the equation leads to 3(4) + 5 > 3(5) + 1, or 17 > 16. Therefore, the equation is statically indeterminate to the 1°.
Using equation 3.4, r = 5, m = 2, Fi = 2. Applying the equation leads to 5 + 2 > 3(2), or 7 > 6. Therefore, the beam is statically indeterminate to the 1°.
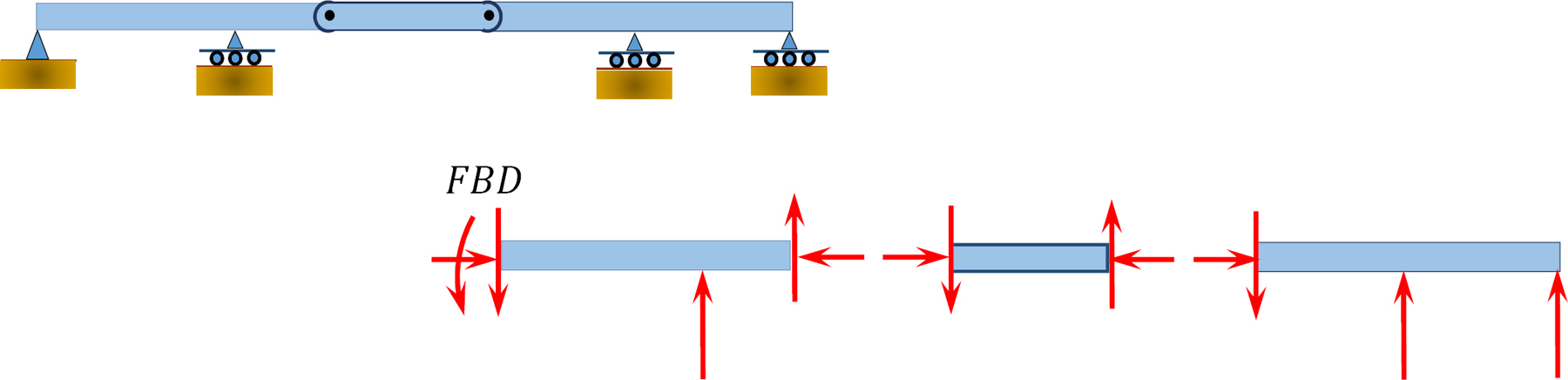
Solution
Using equation 3.3, r = 5, m = 5, c = 2, j = 6. Applying the equation leads to 3(5) + 5 = 3(6) + 2, or 20 = 20. Therefore, the beam is statically determinate.
Using equation 3.4, r = 5, m = 3, Fi = 4. Applying the equation leads to 5 + 4 > 3(3), or 9 = 9. Therefore, the beam is statically determinate.
Example 3.2
Classify the frames shown in Figure 3.6 through Figure 3.8 as stable or unstable and determinate or indeterminate. If indeterminate, state the degree of indeterminacy.

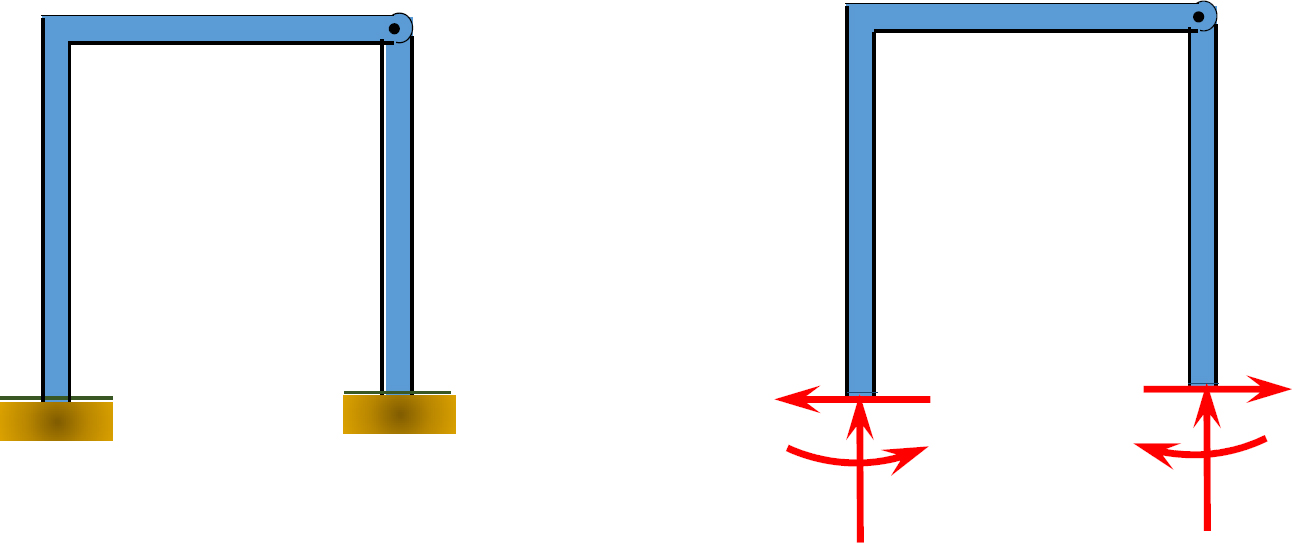
Solution
Using equation 3.3, r = 3, m = 3, c = 0, j = 4. Applying the equation leads to 3(3) + 3 = 3(4) + 0, or 12 = 12. Therefore, the frame is statically determinate.
Using equation 3.4, r = 3, m = 1, Fi = 0. Applying the equation leads to 3 + 0 = (3)(1), or 3 = 3. Therefore, the frame is statically determinate.
Note: When using equation 3.3 for classifying a frame, the frame must be disassembled at its joints to correctly determine the number of members.
Solution
Using equation 3.3, r = 6, m = 3, c = 1, j = 4. Applying the equation leads to 3(3) + 6 > 3(4) + 1, or 15 > 13. Therefore, the frame is statically indeterminate to the 2°.
Using equation 3.4, r = 6, m = 2, Fi = 2. Applying the equation leads to 6 + 2 > 3(2), or 8 > 6. Therefore, the frame is statically indeterminate to the 2°.
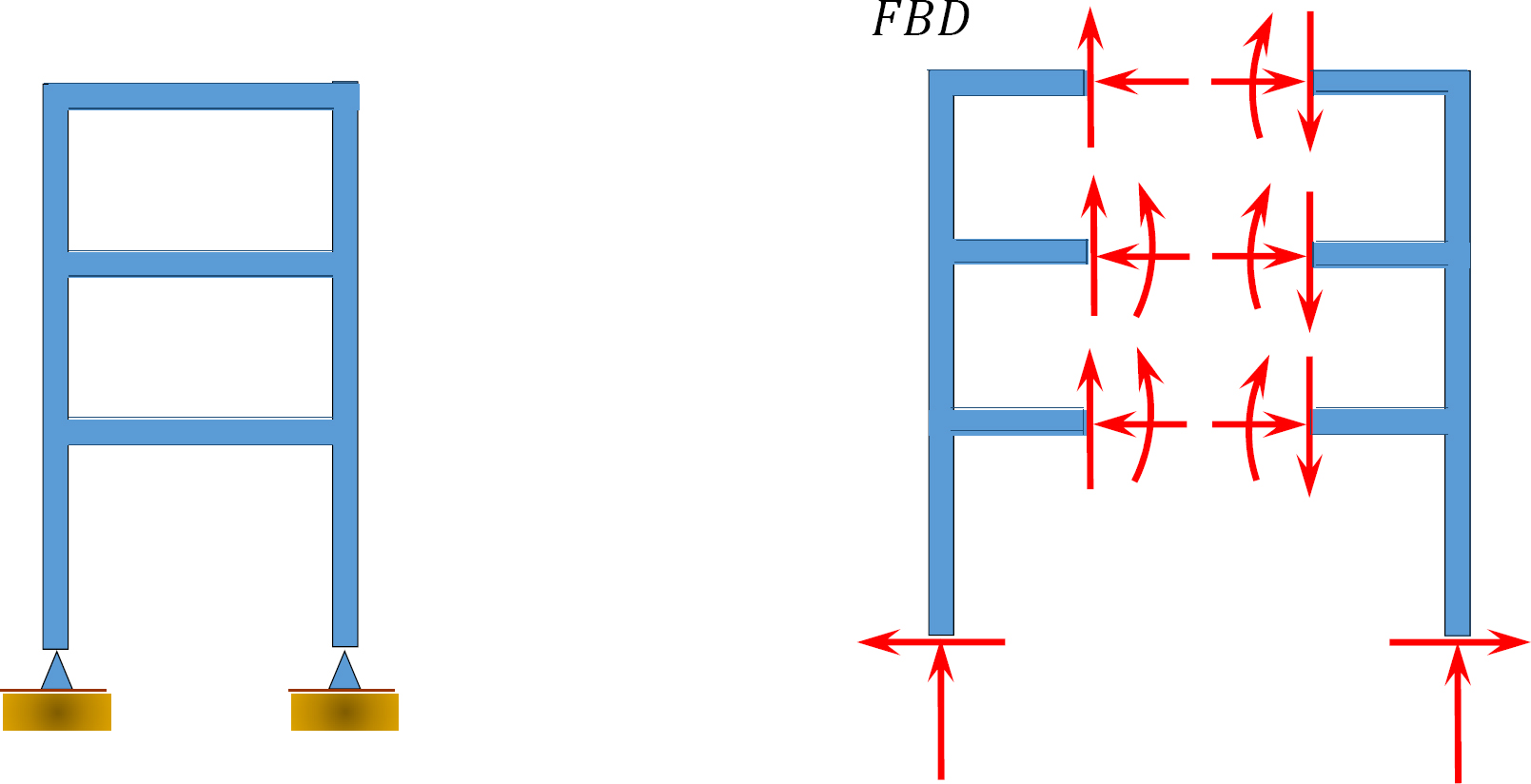
Solution
Using equation 3.3, r = 4, m = 9, c = 0, j = 8. Applying the equation leads to 3(9) + 4 > 3(8) + 0, or 31 > 24. Therefore, the frame is statically indeterminate to the 7°.
Using equation 3.4, r = 4, m = 1, Fi = 9. Applying the equation leads to 4 + 9 > (3)(2), or 13 > 6. Therefore, the frame is statically indeterminate to the 7°.
Note: When using equation 3.4 to classify a frame with a closed loop, as given here, the loop has to be cut open by the method of section, and the internal reactions in the cut section should be considered in the analysis.
3.4 Computation of Support Reactions for Planar Structures
The support reactions for statically determinate and stable structures on a plane are determined by using the equations of equilibrium. The procedure for computation is outlined below.
Procedure for Computation of Support Reactions
•Sketch a free-body diagram of the structure, identifying all the unknown reactions using an arrow diagram.
•Check the stability and determinacy of the structure using equation 3.3 or 3.4. If the structure is classified as determinate, proceed with the analysis.
•Determine the unknown reactions by applying the three equations of equilibrium. If a computed reaction results in a negative answer, the initially assumed direction of the unknown reaction, as indicated by the arrow head on the free-body diagram, is wrong and should be corrected to show the opposite direction. Once the correction is made, the magnitude of the force should be indicated as a positive number in the corrected arrow head on the free-body diagram
Example 3.3
A cantilever beam is subjected to a uniformly distributed load and an inclined concentrated load, as shown in figure 3.9a. Determine the reactions at support A.
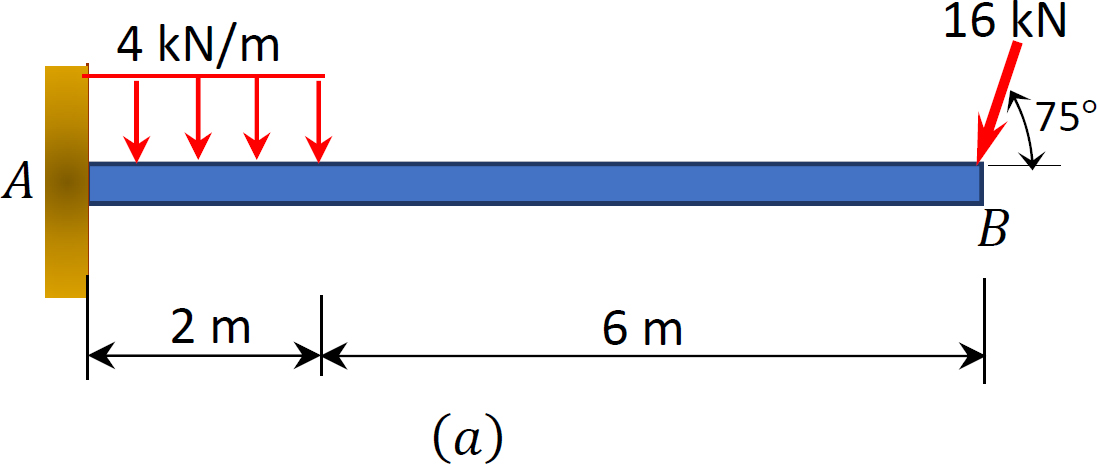
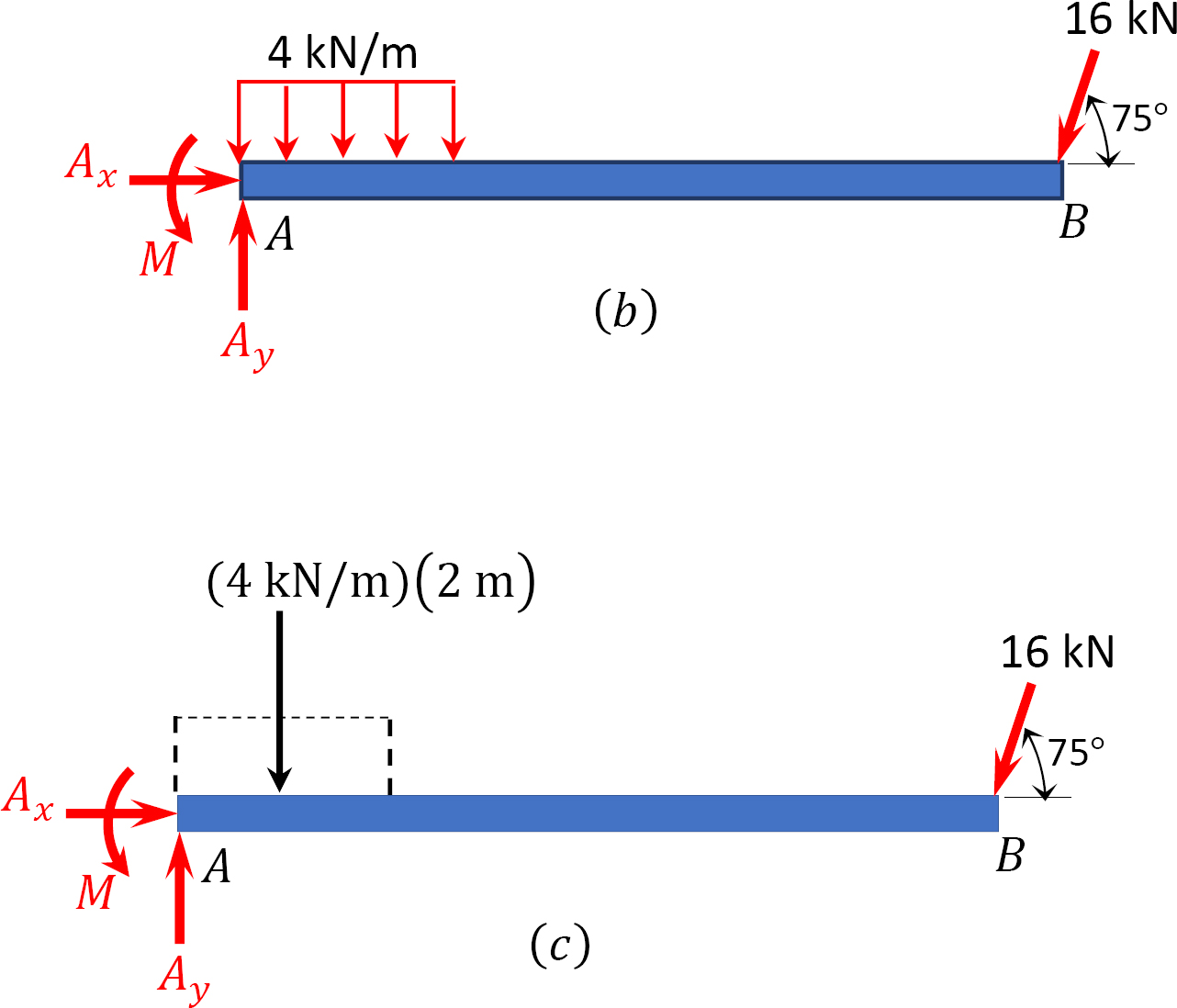
Solution
Free-body diagram. The free-body diagram of the entire beam is shown in Figure 3.9b. The support reactions, as indicated in the free-body diagram, are Ay, Ax, and M.
Computation of reactions. Prior to the computation of the support reactions, the distributed loading should be replaced by a single resultant force, and the inclined loading resolved to the vertical and horizontal components. The magnitude of the resultant force is equal to the area under the rectangular loading, and it acts through the centroid of the rectangle. As seen in Figure 3.9c, P = [(4 kN/m)(2 m)], and its location is at the centroid of the rectangle loading 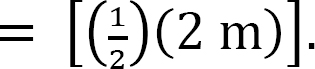 Applying the equations of static equilibrium provides the following:
Applying the equations of static equilibrium provides the following:
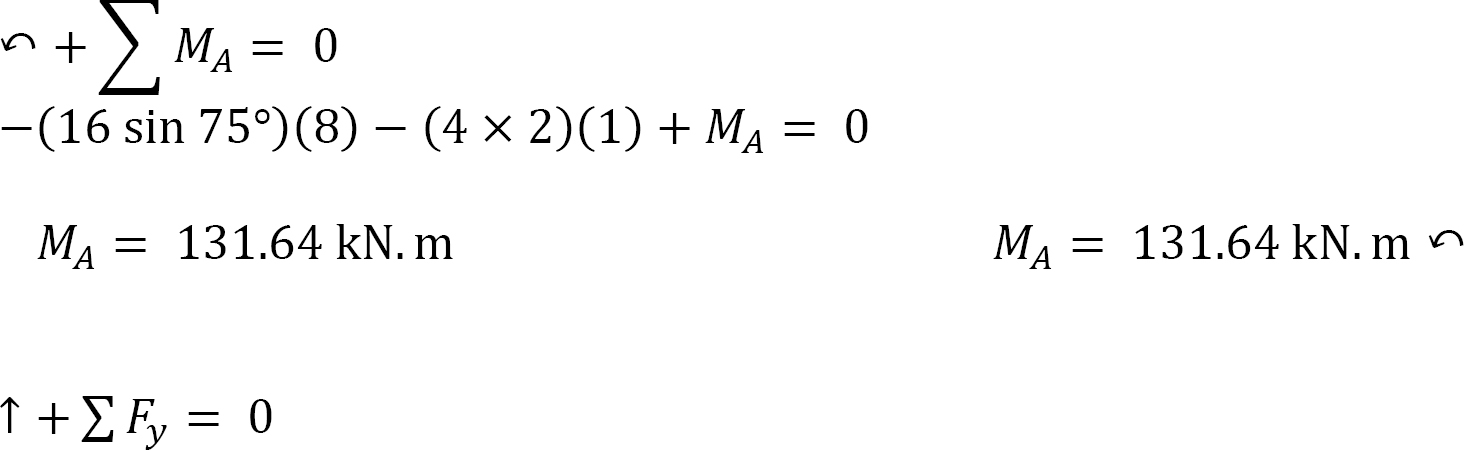
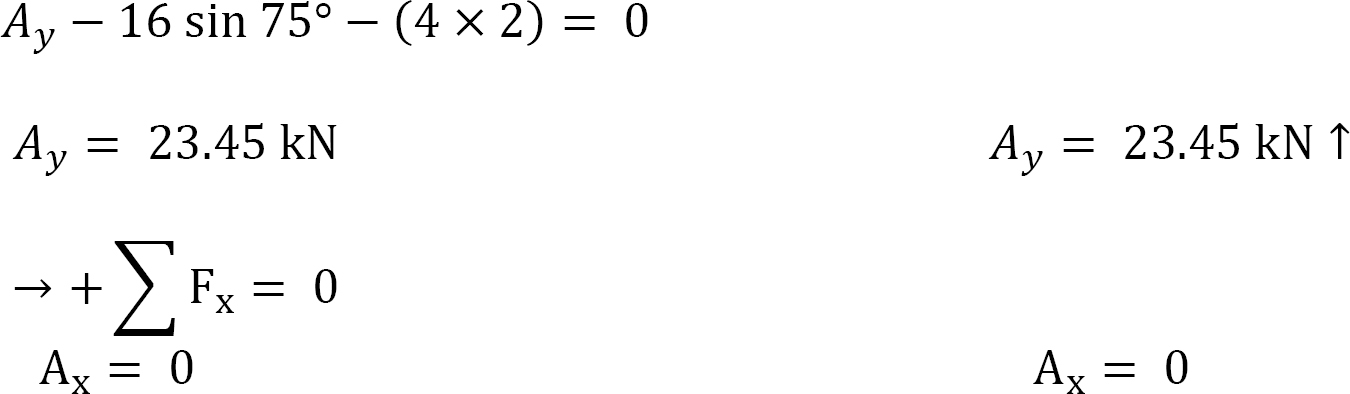
Example 3.4
A 12ft-long simple beam carries a uniformly distributed load of 2 kips/ft over its entire span and a concentrated load of 8 kips at its midspan, as shown in Figure 3.10a. Determine the reactions at the supports A and B of the beam.
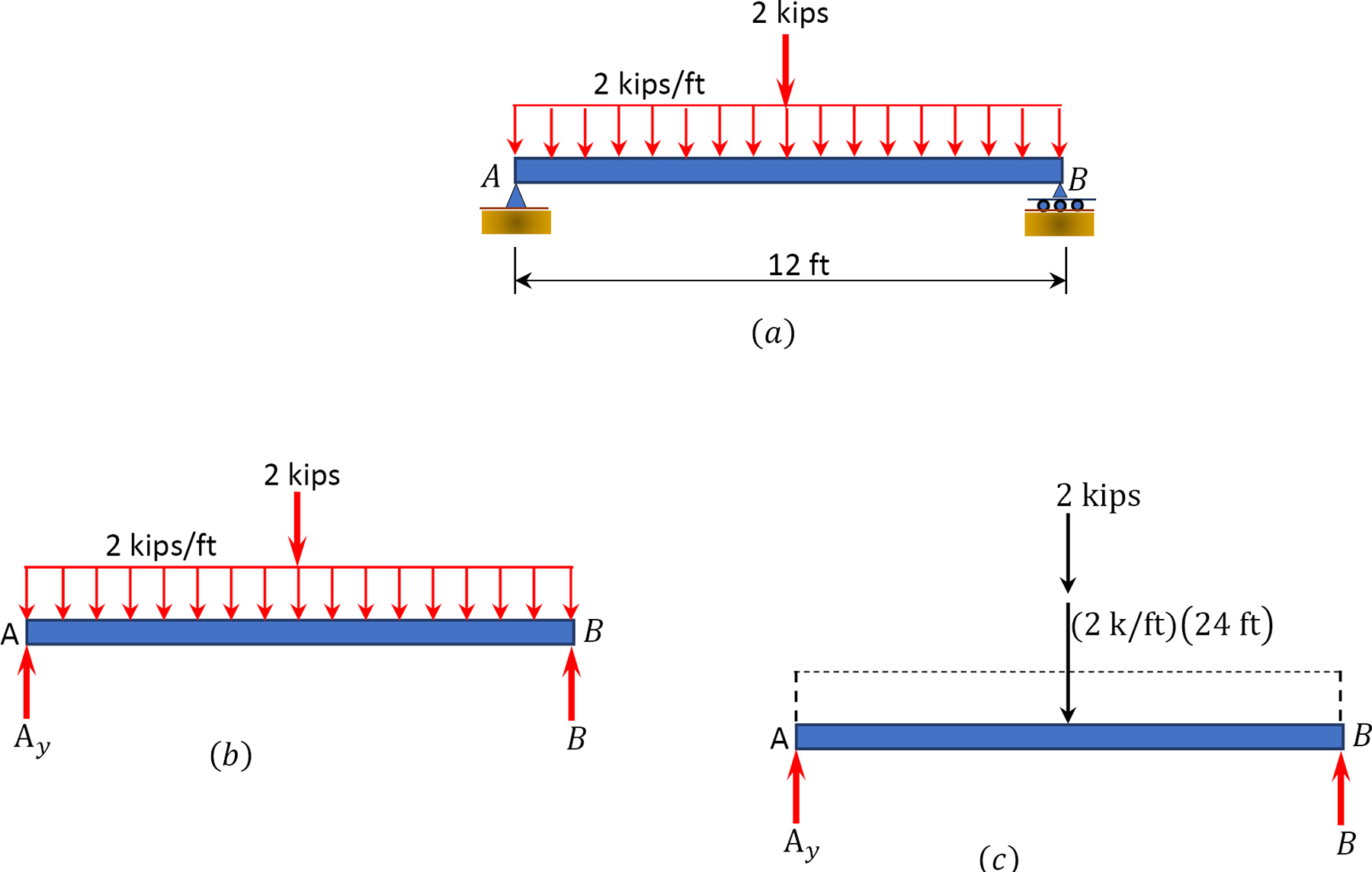
Solution
Free-body diagram. The free-body diagram of the entire beam is shown in Figure 3.10b.
Computation of reactions. The distributed loading is first replaced with a single resultant force, as seen in Figure 3.10c. The magnitude of the resultant force is equal to the area of the rectangular loading (distributed force). Thus, P = [(2 k/ft)(12 ft)], and its location is at the centroid of the rectangular loading 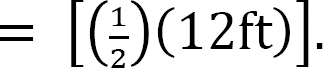 Since there is a symmetry in loading in this example, the reactions at both ends of the beam are equal, and they could be determined using the equations of static equilibrium and the principle of superposition, as follows:
Since there is a symmetry in loading in this example, the reactions at both ends of the beam are equal, and they could be determined using the equations of static equilibrium and the principle of superposition, as follows:

Example 3.5
A beam with an overhang is subjected to a varying load, as shown in Figure 3.11a. Determine the reactions at supports A and B.
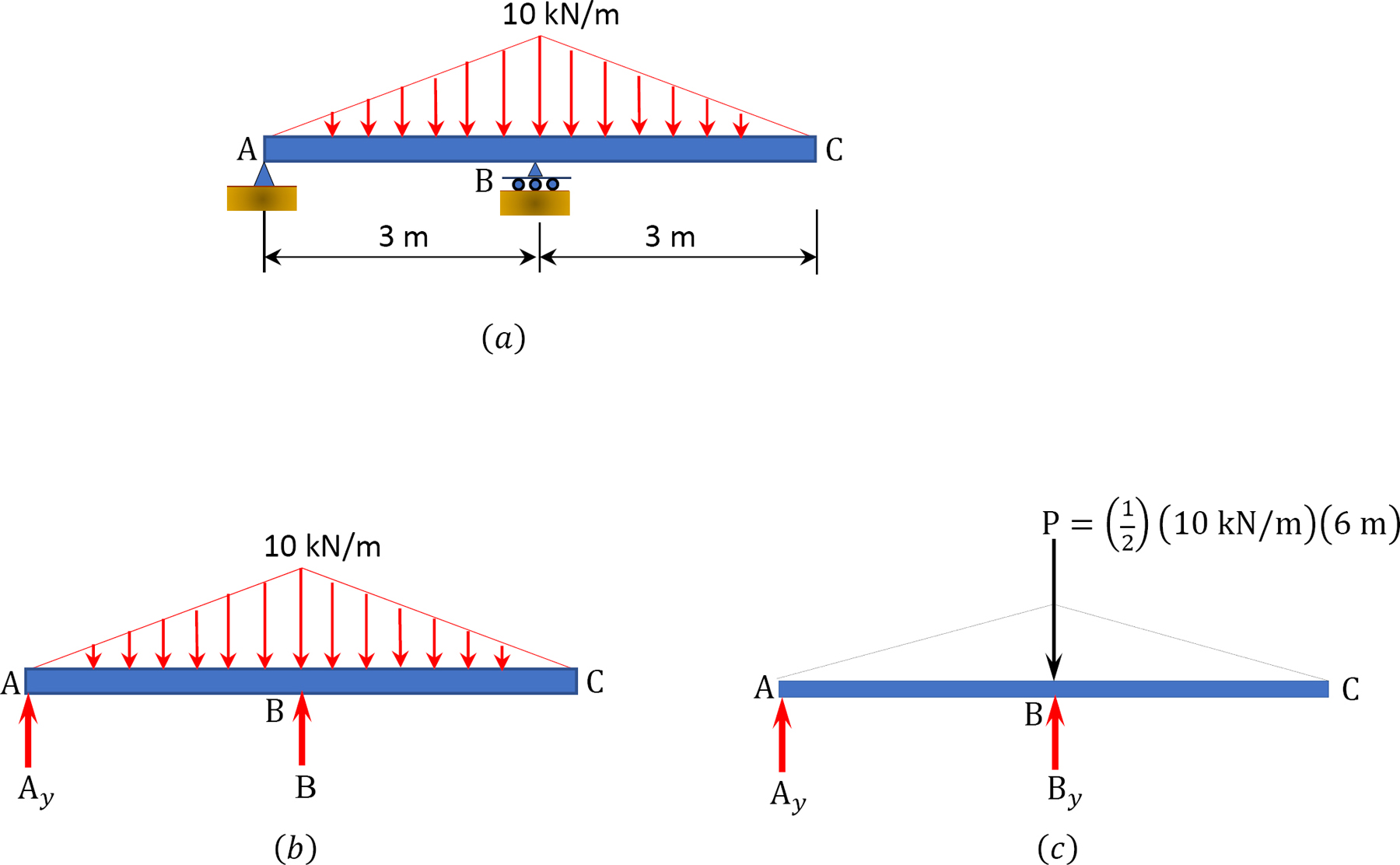
Solution
Free-body diagram. The free-body diagram of the entire beam is shown in Figure 3.11b.
Computation of reactions. Observe that the distributed loading in the beam is triangular. The distributed load is first replaced with a single resultant force, as shown in Figure 3.11c. The magnitude of the single resultant force is equal to the area under the triangular loading. Thus, P = (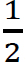 )(6 m)(10 kN/m), and its centroid is at the center of the loading (6m). Applying the equations of equilibrium provides the following:
)(6 m)(10 kN/m), and its centroid is at the center of the loading (6m). Applying the equations of equilibrium provides the following:
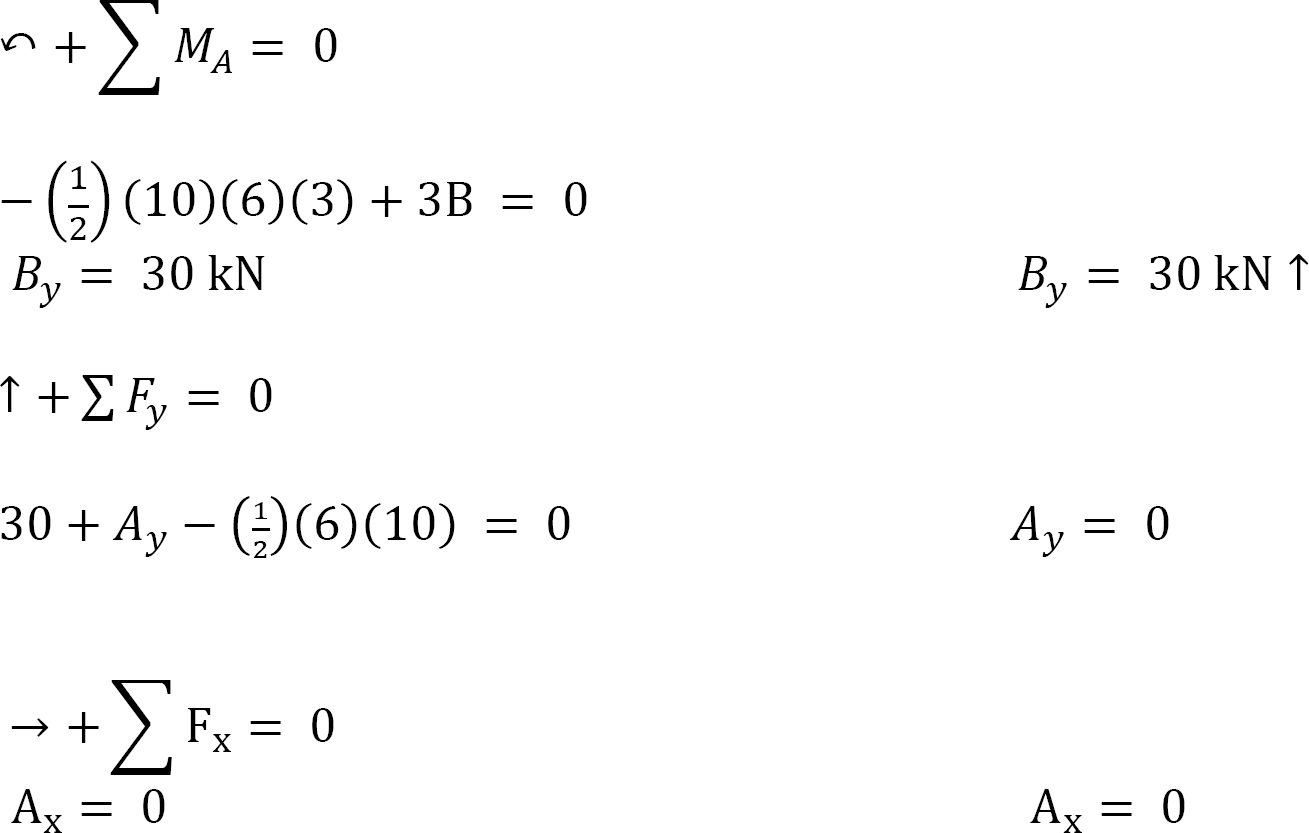
Example 3.6
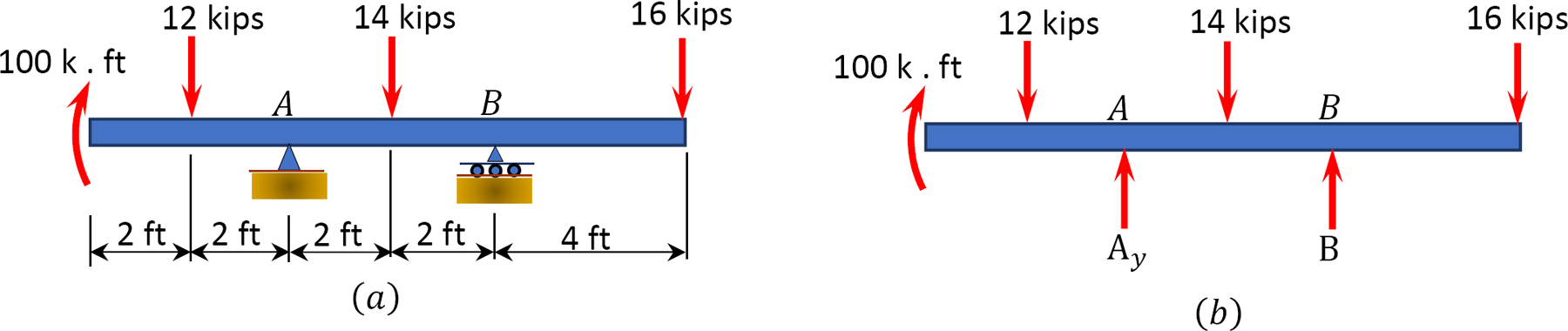
A beam with overhanging ends supports three concentrated loads of 12 kips, 14 kips, and 16 kips and a moment of 100 kips.ft, as shown in Figure 3.12a. Determine the reactions at supports A and B.
Solution
Free-body diagram. The free-body diagram of the beam is shown in Figure 3.12b.
Computation of reactions. Applying the equations of equilibrium provides the following:
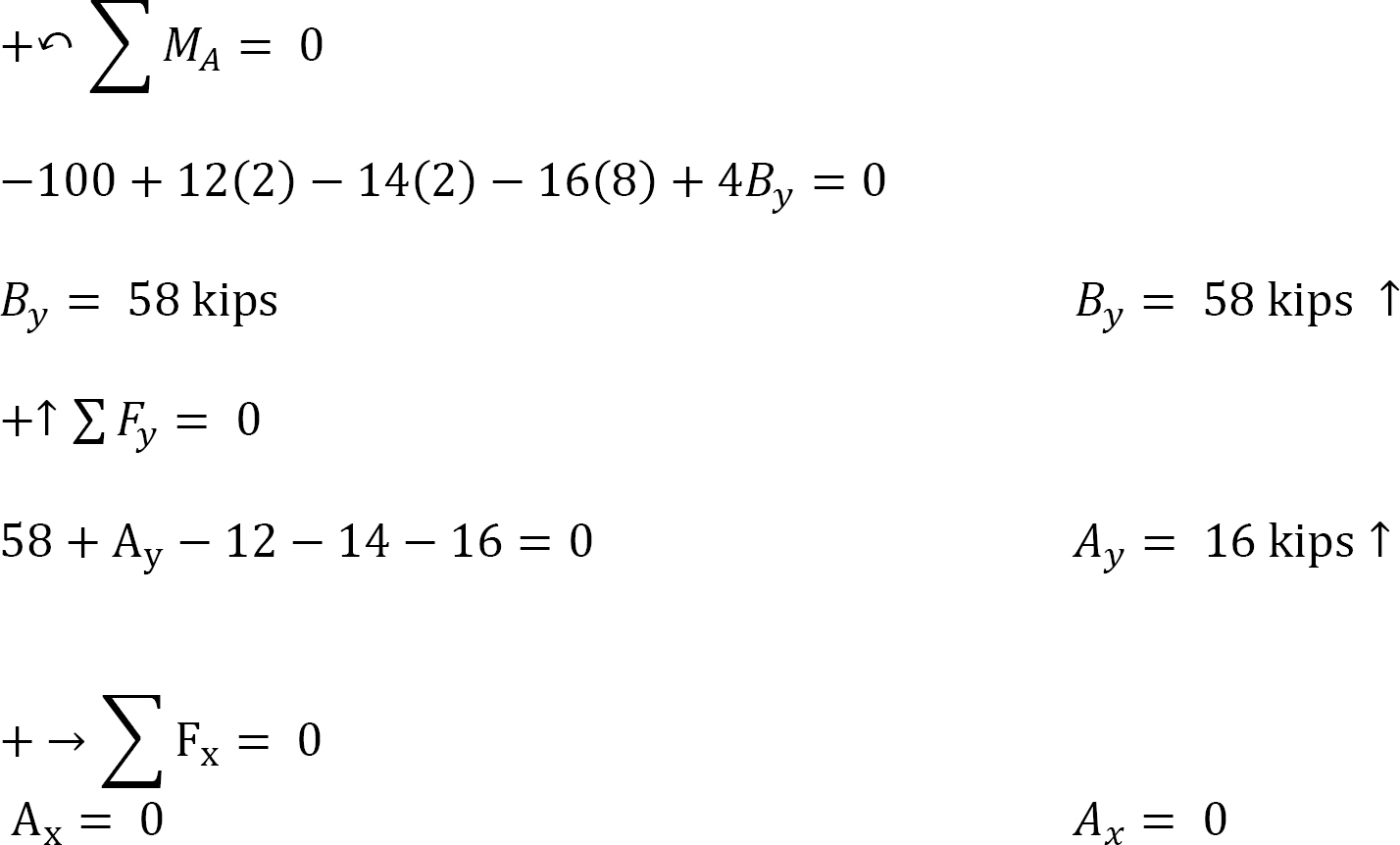
Example 3.7
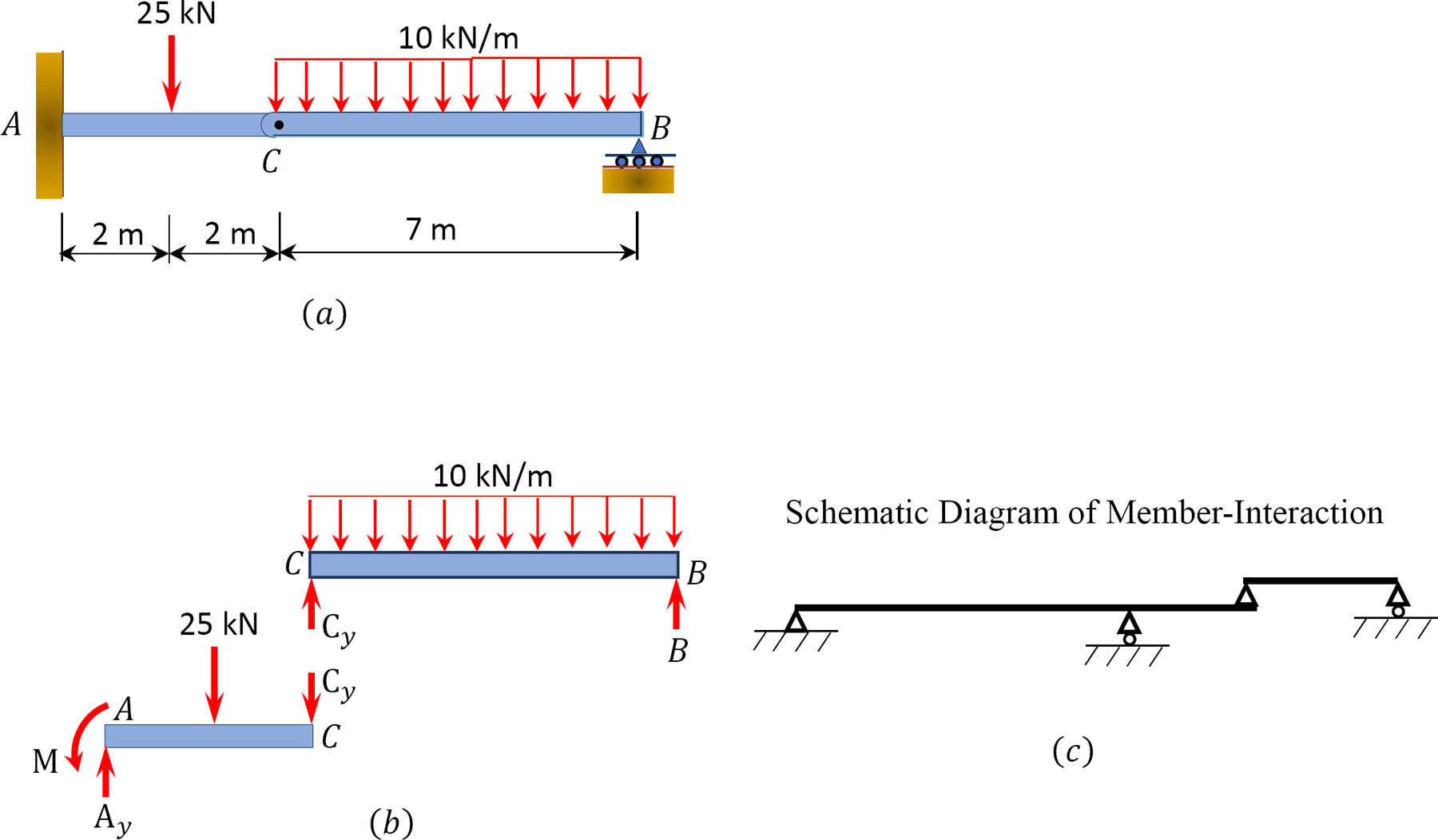
A compound beam is subjected to the loads shown in Figure 3.13a. Find the support reactions at A and B of the beam.
Solution
Free-body diagram. The free-body diagram of the entire beam is shown in Figure 3.13b.
Identification of primary and complimentary structures. For correct analysis of a compound structure, the primary and the complimentary parts of the structure should be identified for proper understanding of their interaction. The interaction of these parts are shown in Figure 3.13c. The primary structure is the part of the compound structure that can sustain the applied external load without the assistance of the complimentary structure. On the other hand, the complimentary structure is the part of the compound structure that depends on the primary structure to support the applied external load. For the given structure, part AC is the primary structure, while part CB is the complimentary structure.
Computation of reactions. The analysis of a compound structure must always begin with the analysis of the complimentary structure, as the complimentary structure is supported by the primary structure. Using the equations of equilibrium, the support reactions of the beam are determined as follows:
Analysis of the complimentary structure CB.
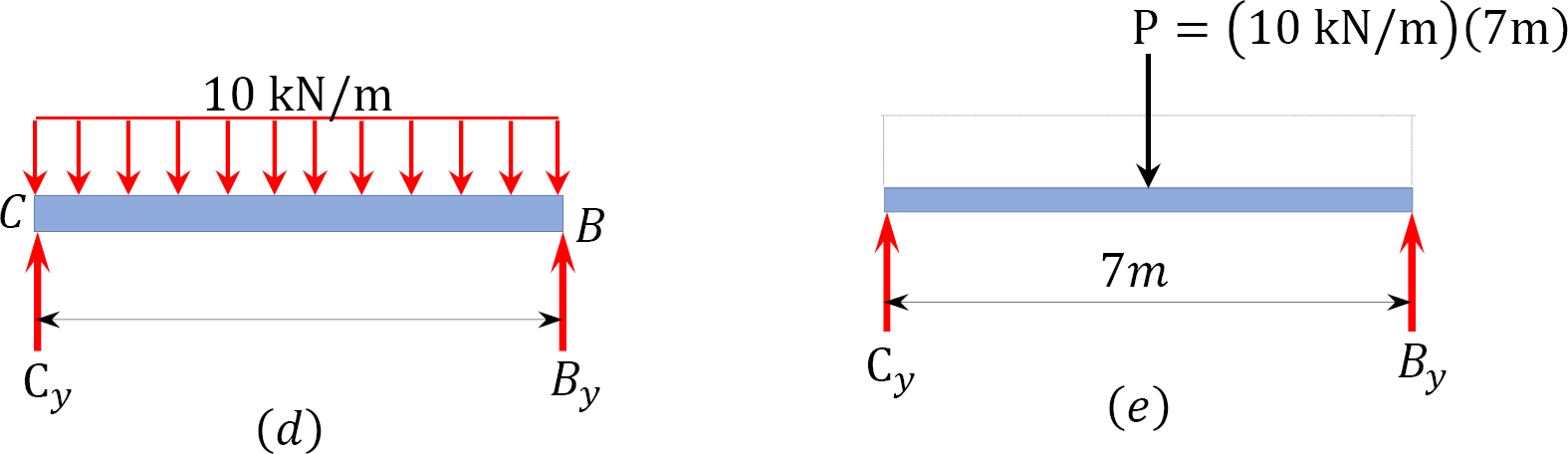

Analysis of the primary structure AC.

Computation of support reaction. Note that prior to the computation of the reactions, the reaction at point C in the complimentary structure is applied to the primary structure as a load. The magnitude of the applied load is the same as that of the complimentary structure, but it is opposite in direction. Applying the equations of equilibrium suggests the following:



Example 3.8
Find the reactions at supports A, C, and E of the compound beam carrying a uniformly distributed load of 10 kips/ft over its entire length as shown in figure 3.14a.
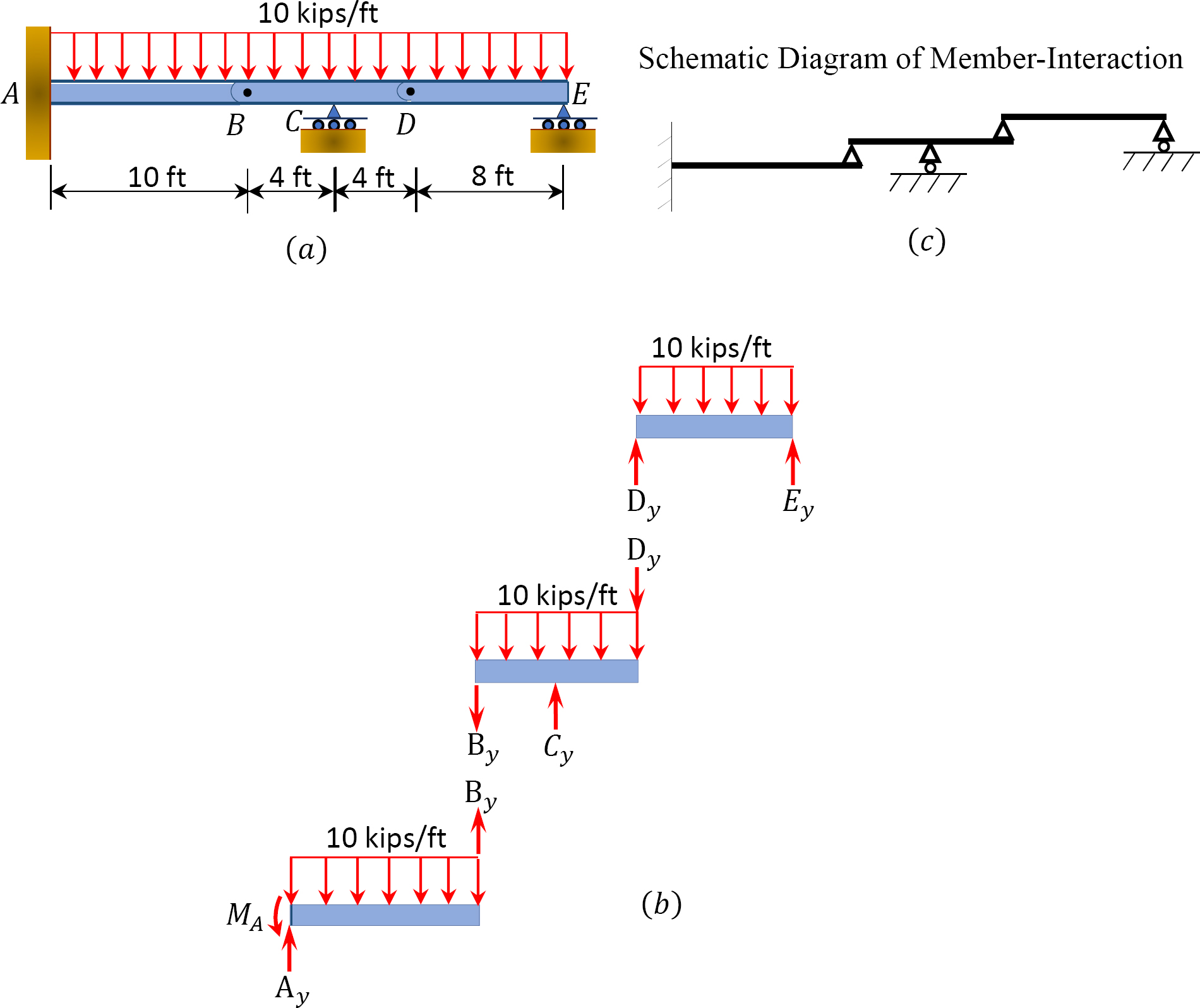
Solution
Free-body diagram. The free-body diagram of the entire beam is shown in Figure 3.14b.
Identification of primary and complimentary structures. The interaction diagram for the given structure is shown in Figure 3.14c. AB is the primary structure, while BD and DE are the complimentary structures.
Computation of reactions.
Analysis of complimentary structure DE.
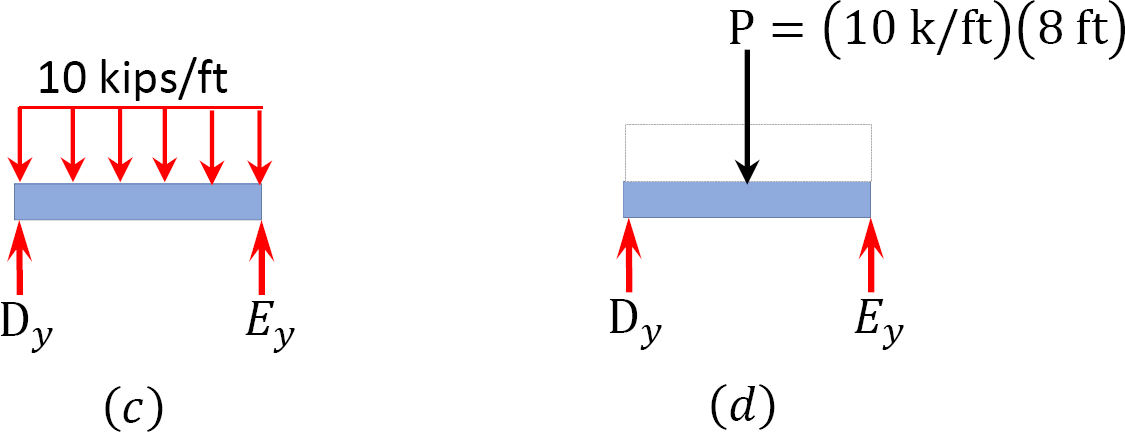

Analysis of complimentary structure BD.


Analysis of primary structure AB.

Computation of support reaction. Note that prior to the computation of the reactions, the uniform load is replaced by a single resultant force, and the reaction at point B in the complimentary structure is applied to the primary structure as a load. Applying the equilibrium requirement yields the following:
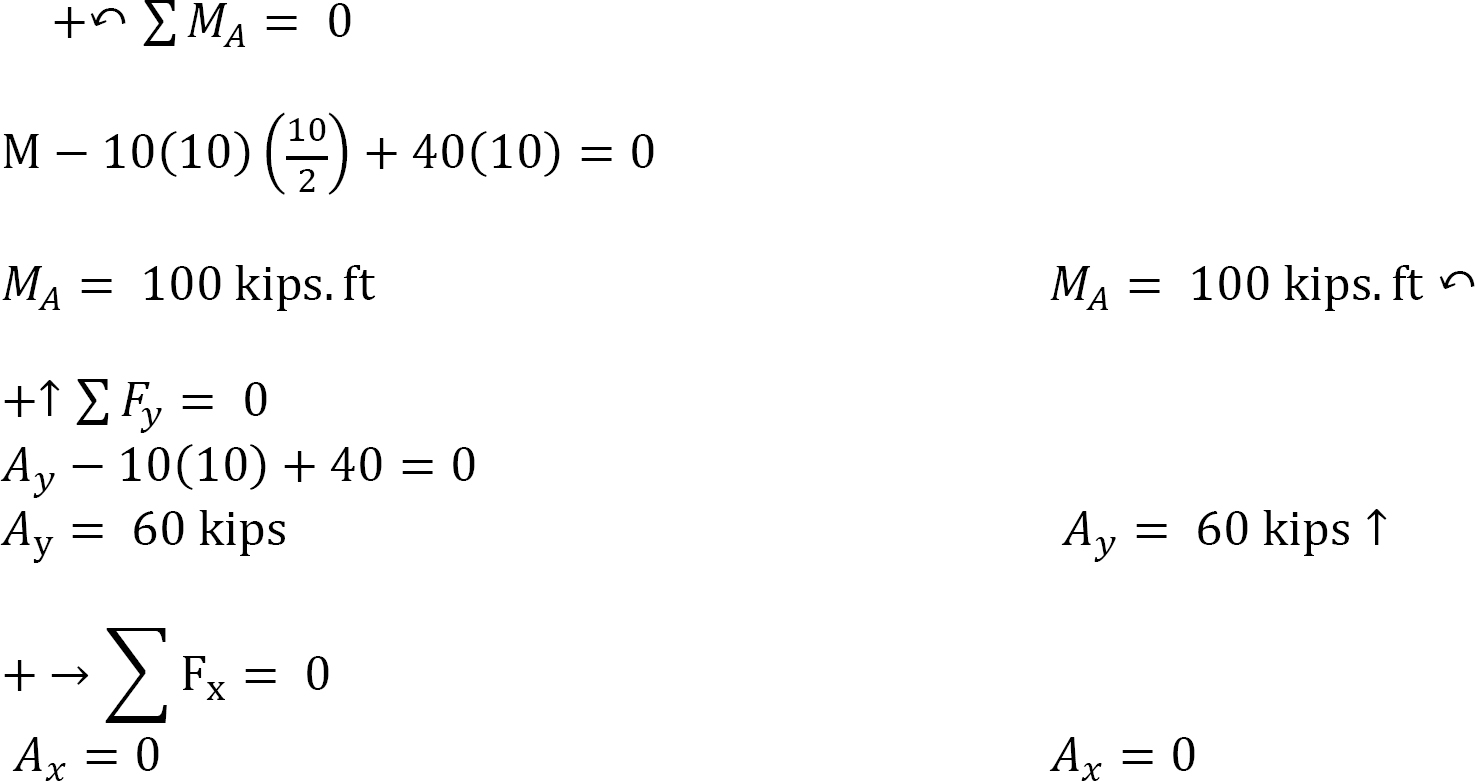
Example 3.9
Find the reactions at supports A, B, E, and F of the loaded compound beam, as shown in Figure 3.15a.
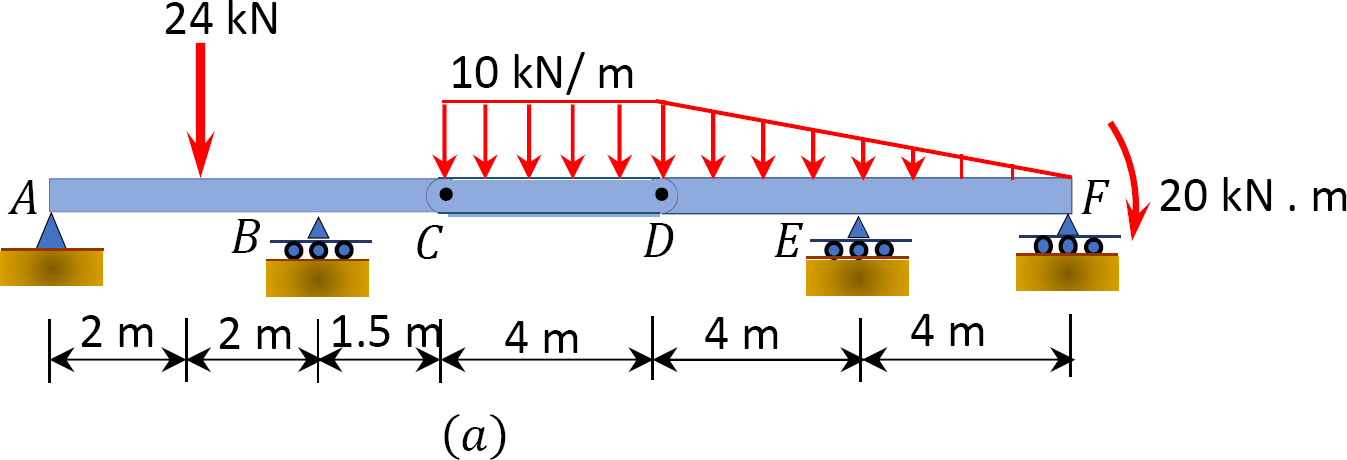
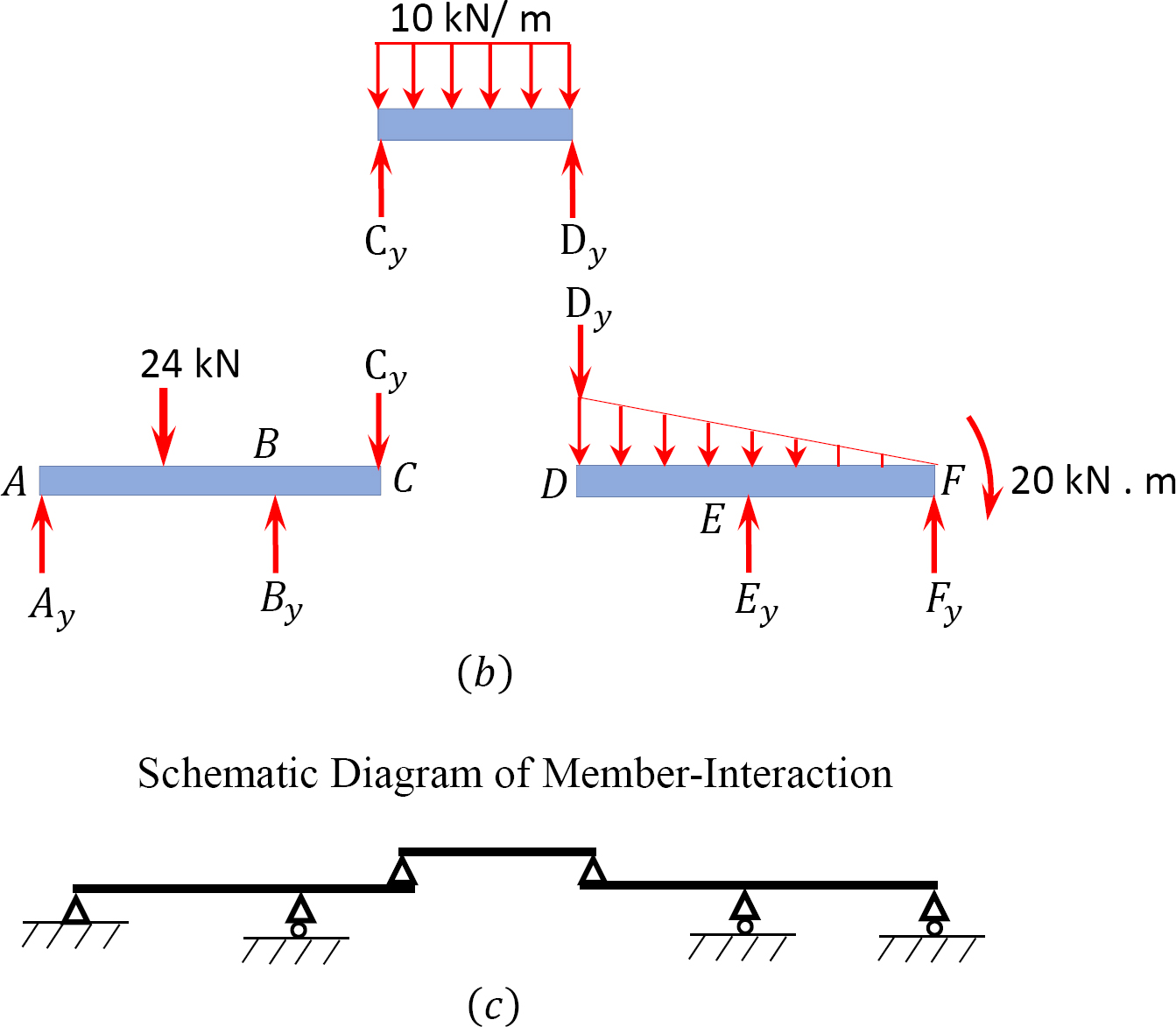
Solution
Free-body diagram. The free-body diagram of the entire beam is shown in Figure 3.15b.
Identification of primary and complimentary structure. The interaction diagram for the given structure is shown in Figure 3.15c. CD is the complimentary structure, while AC and DF are the primary structures.
Computation of reactions.
Analysis of complimentary structure CD.

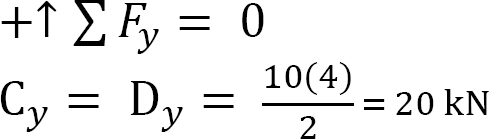
Analysis of primary structure AC.
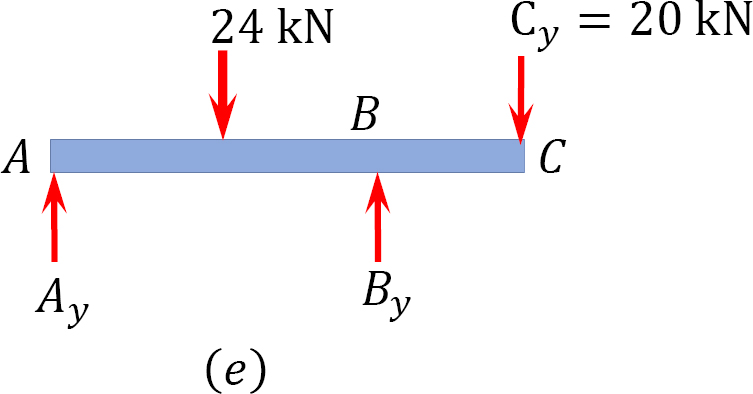
Computation of support reaction. Note that the reaction at C of the complimentary structure is applied as a downward force of the same magnitude at the same point on the primary structure. Applying the equation of equilibrium suggests the following:
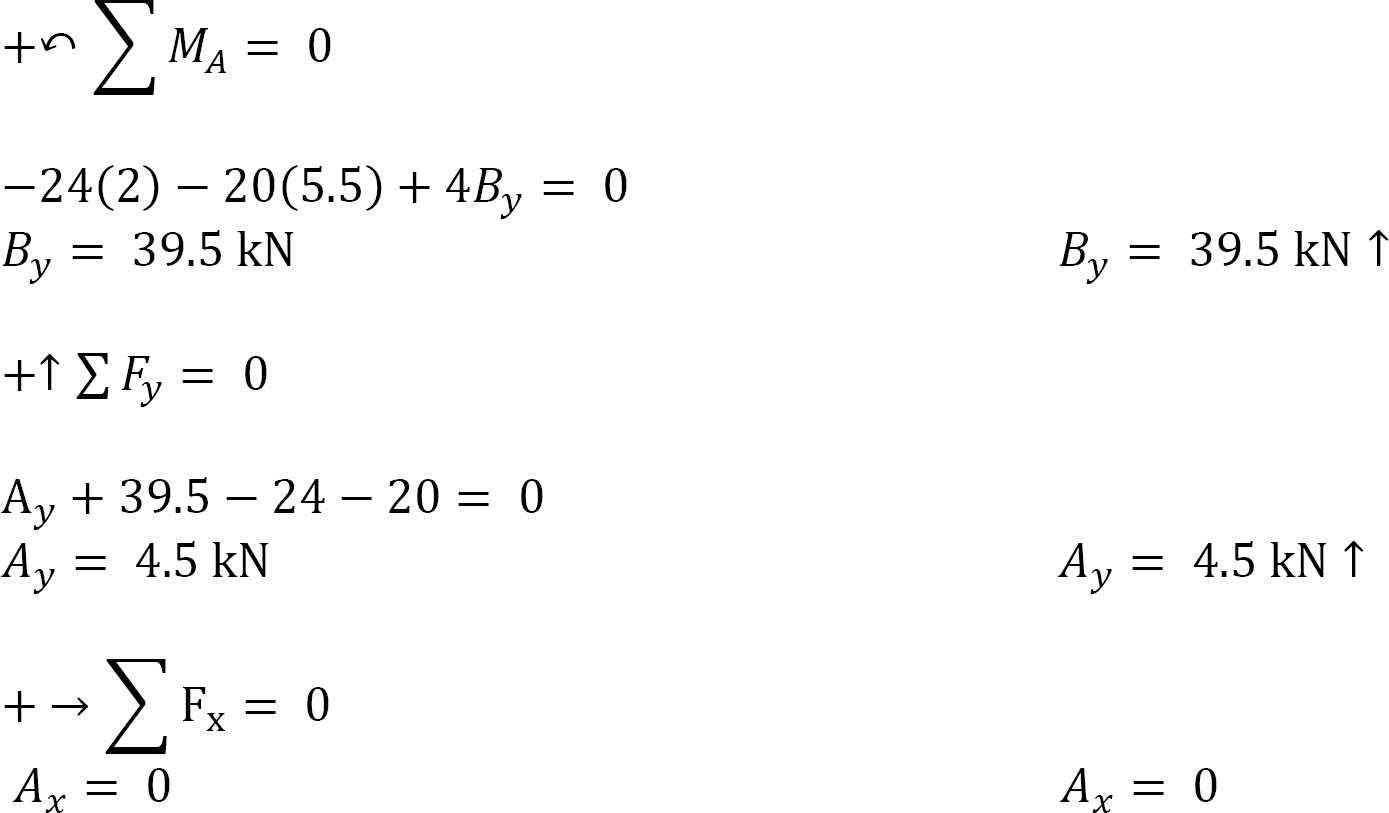
Analysis of primary structure DF.
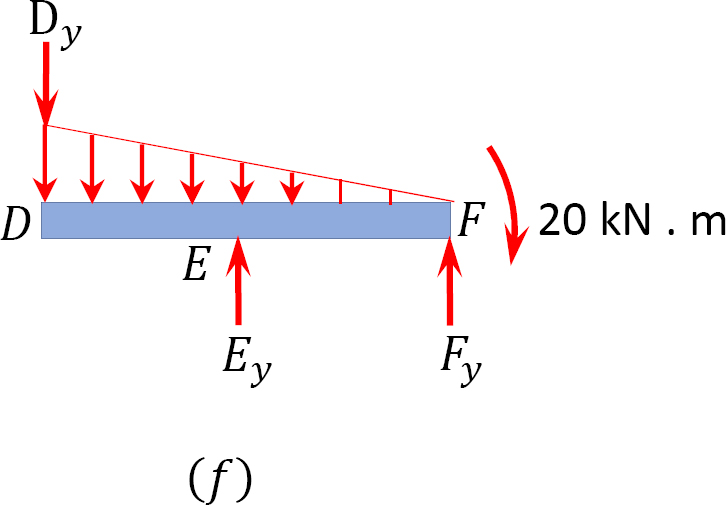
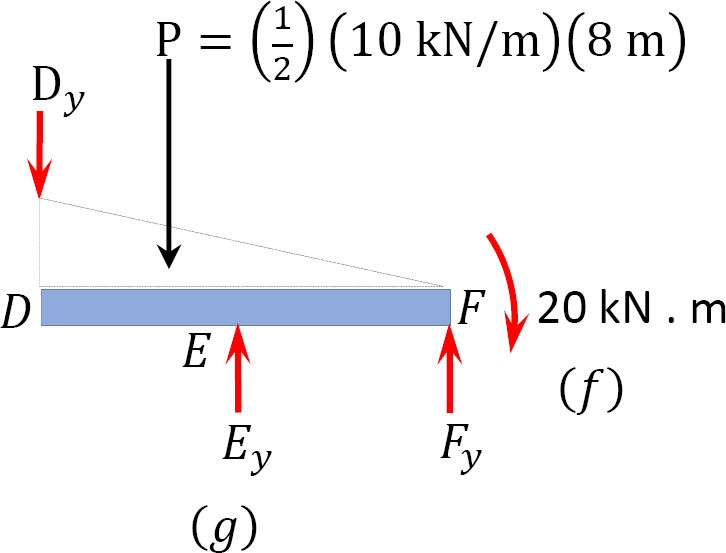
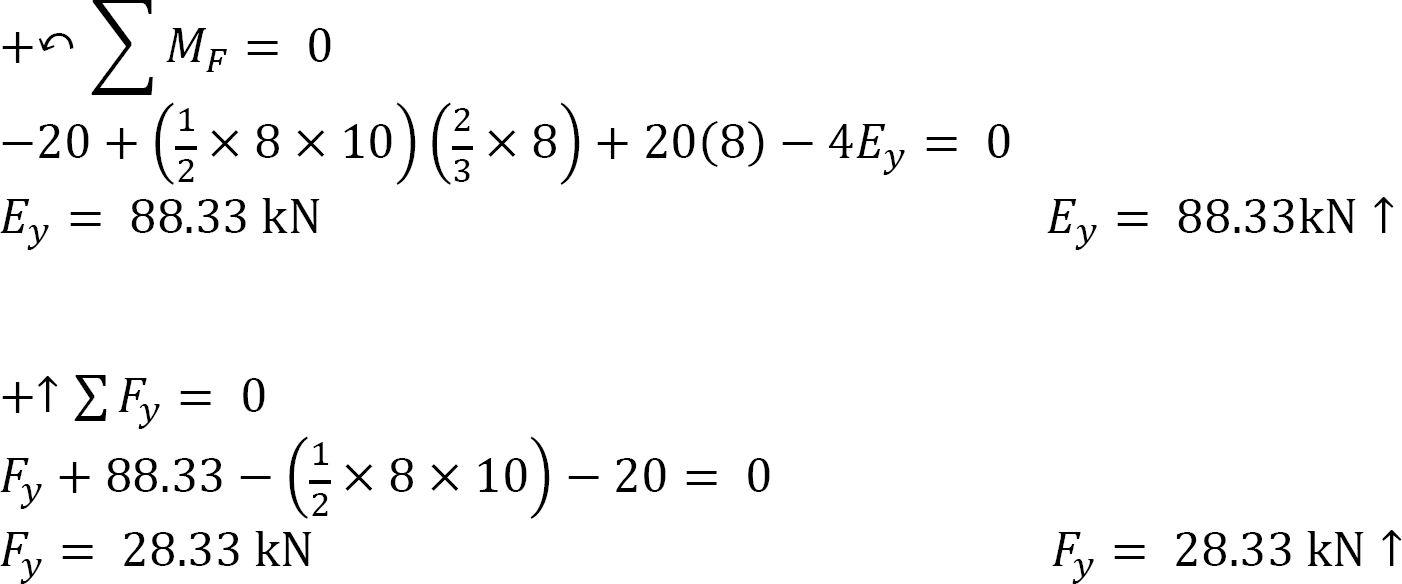
Example 3.10
Determine the reactions at supports A and D of the frame shown in Figure 3.16a.
Solution
Free-body diagram. The free-body diagram of the entire beam is shown in Figure 3.16b.
Computation of reactions. The distributed loads in column AB and beam BC are first replaced by single resultant forces determined as the area of their respective shade of loading, as shown in Figure 3.16c. Applying the conditions of equilibrium suggests the following:

Example 3.11
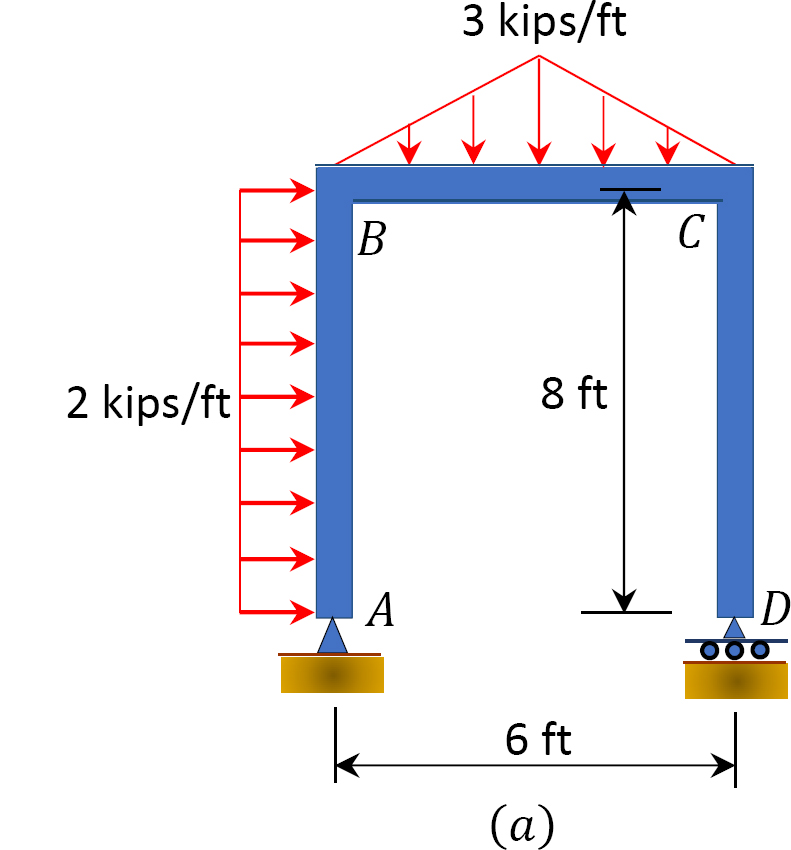
A rigid frame is loaded as shown in Figure 3.17a. Determine the reactions at support D.
Solution
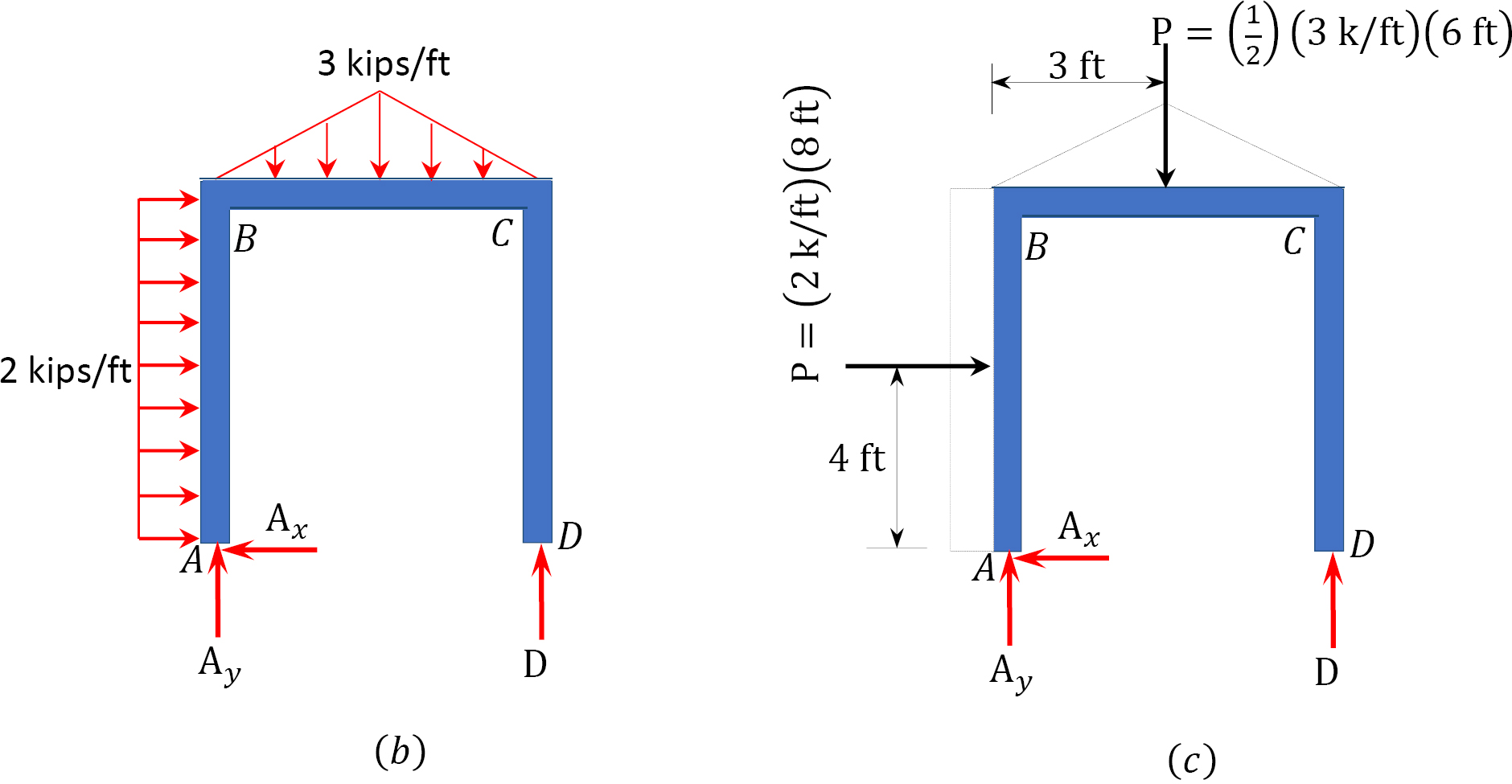
Free-body diagram. The free-body diagram of the entire beam is shown in Figure 3.17b.
Computation of reactions. The distributed load in portion AB of the frame is first replaced with a single resultant force, as shown in Figure 3.17c. Applying the equations of equilibrium suggests the following:
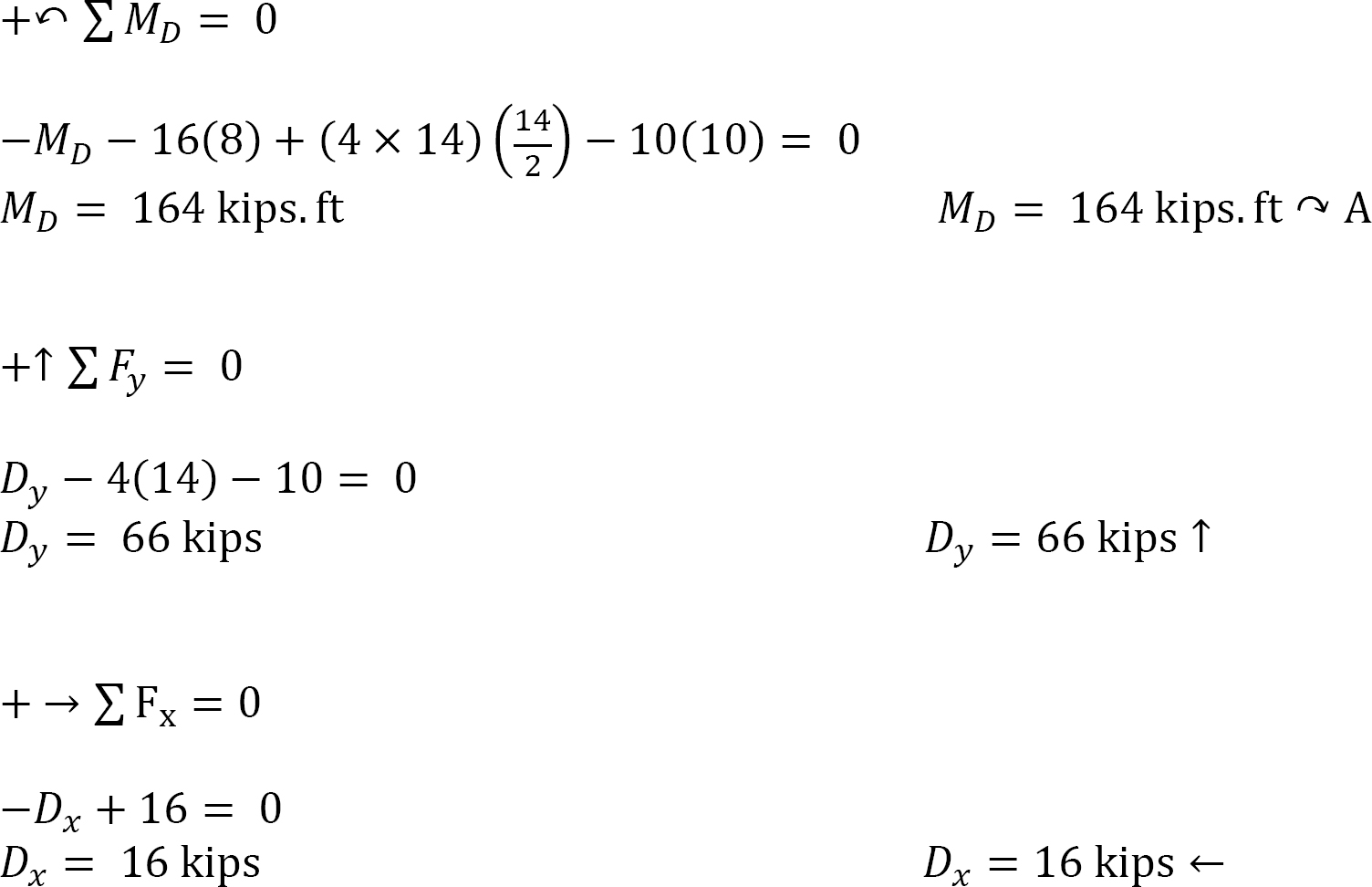
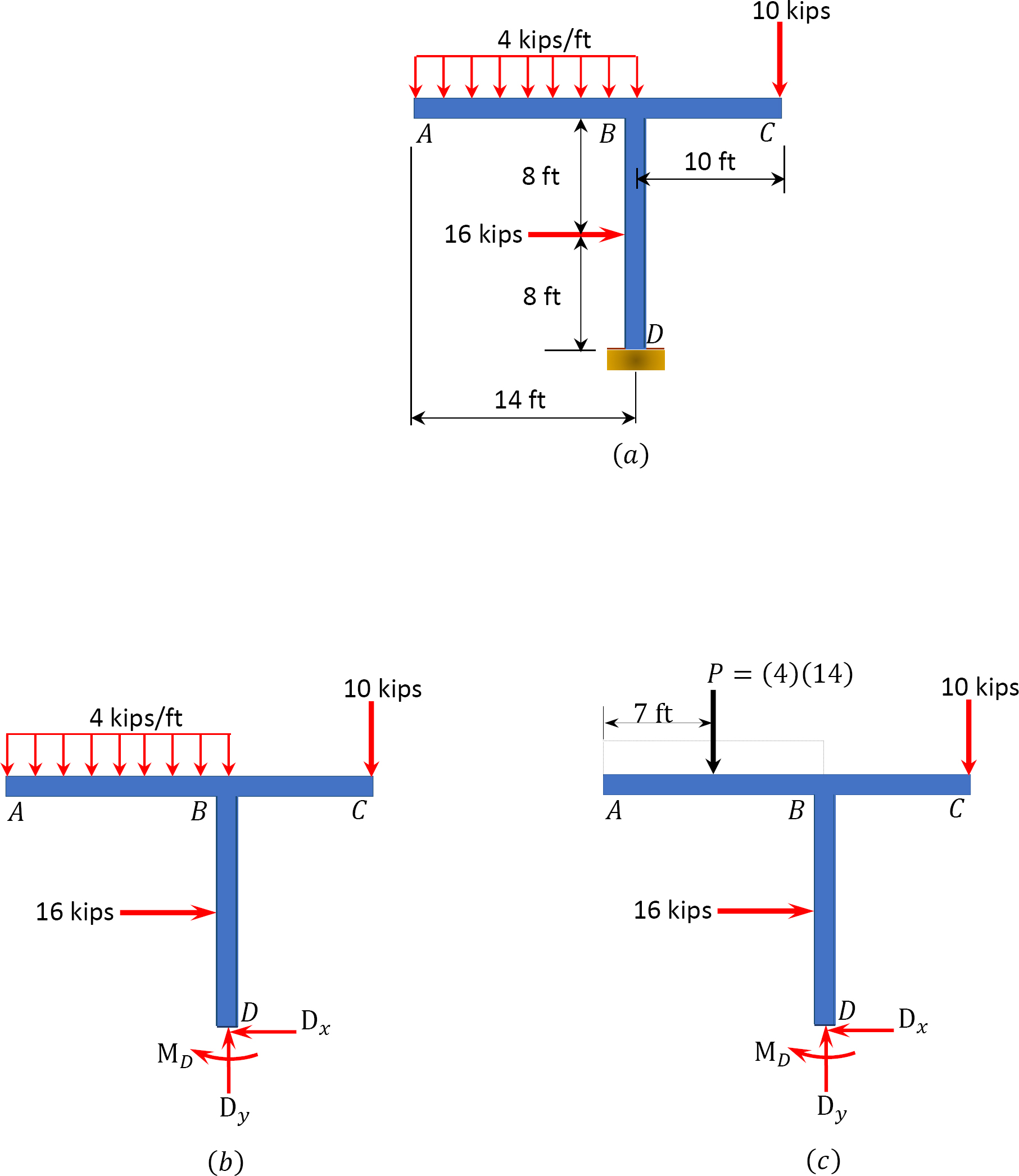
Example 3.12
Find the reactions at supports E and F of the frame shown in Figure 3.18a.

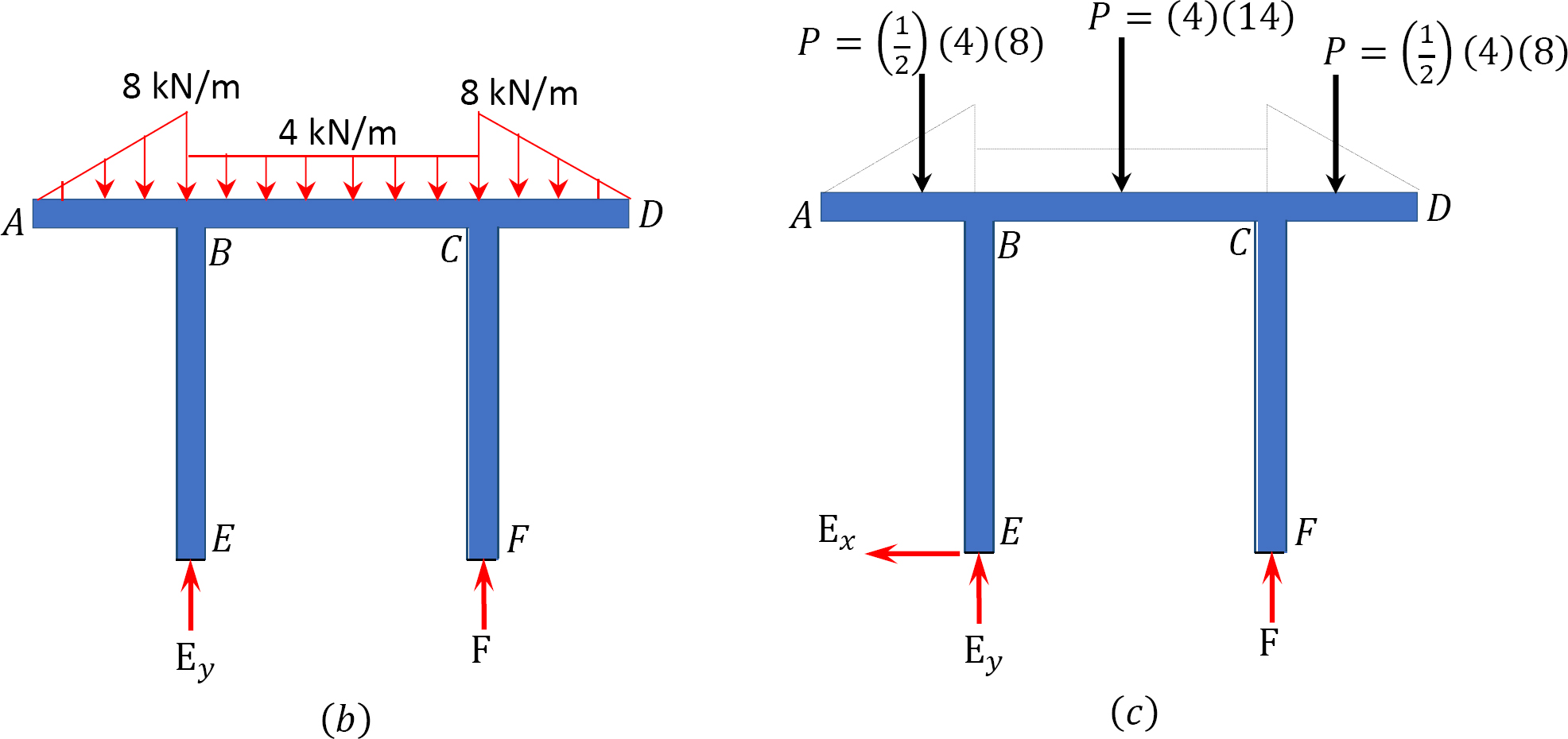
Solution
Free-body diagram. The free-body diagram of the frame is shown in Figure 3.18b.
Computation of reactions. The distributed loads are first replaced with single resultant forces, as shown in Figure 3.18c. Applying the equations of static equilibrium suggests the following:
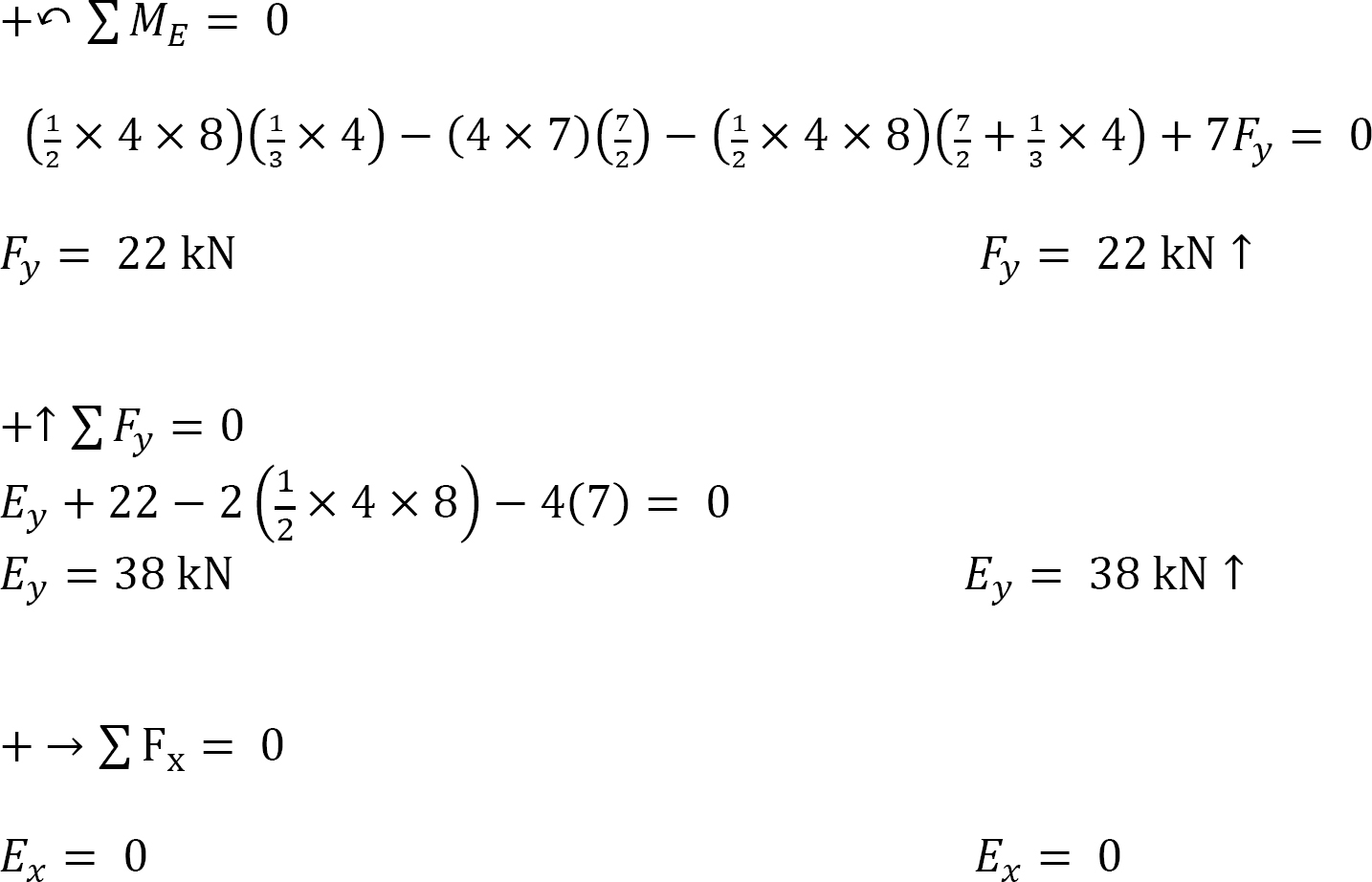
Example 3.13
Determine the reactions at support A of the rigid frame shown in Figure 3.19a.
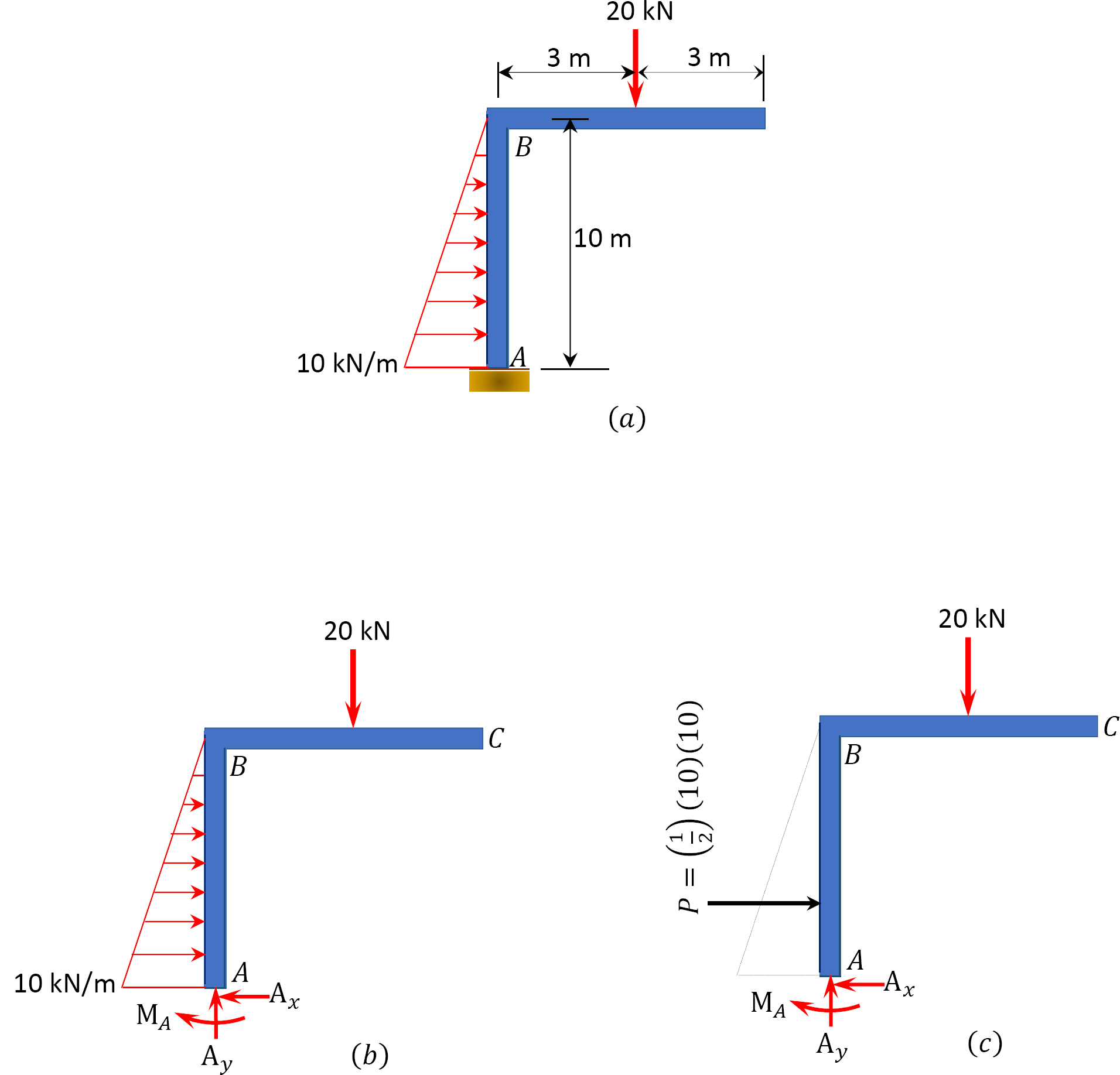
Solution
Free-body diagram. The free-body diagram of the frame is shown in Figure 3.19b.
Computation of reactions. The distributed load in column AB is first replaced with a single resultant force, as shown in Figure 3.19c. Applying the equations of static equilibrium suggests the following:
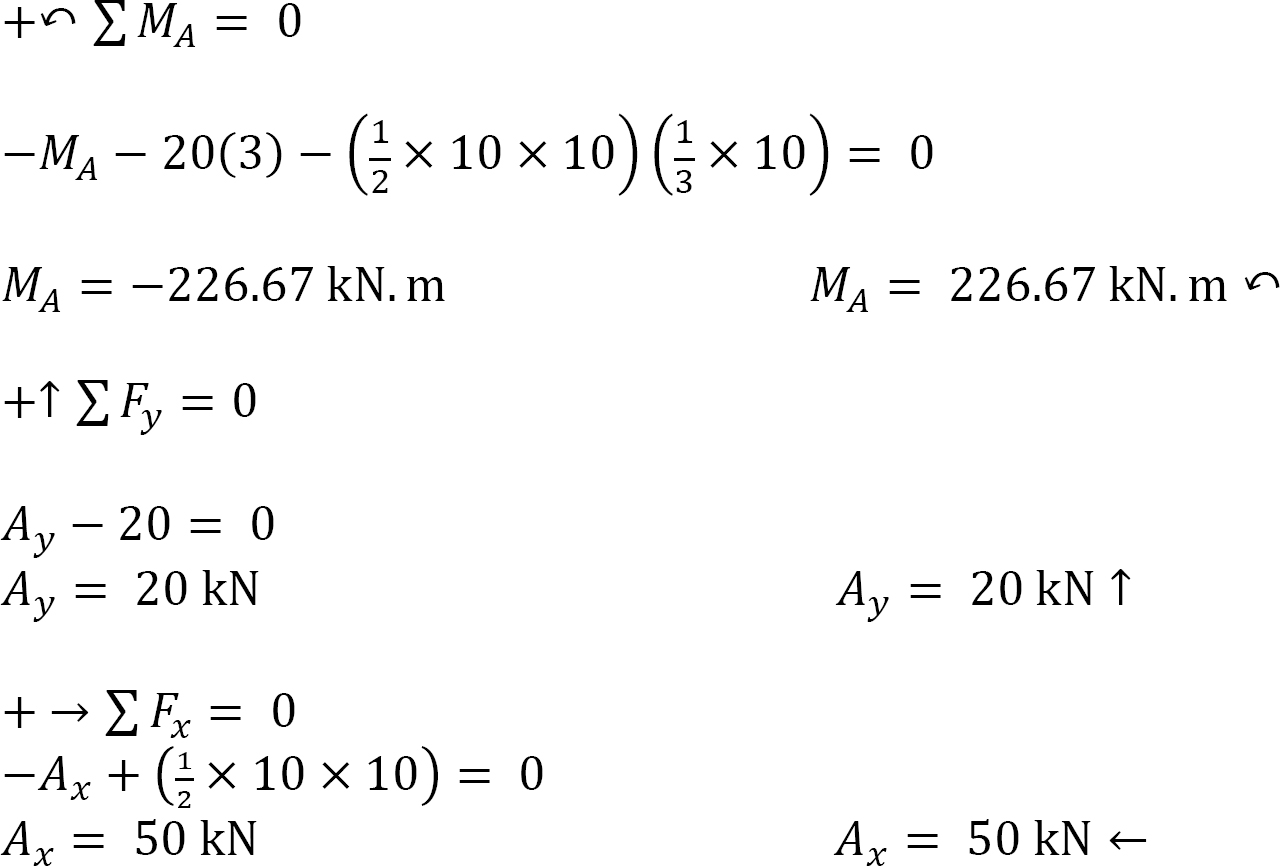
Example 3.14
Determine the reactions at supports A and E of the frame hinged at C, as shown in Figure 3.20a.
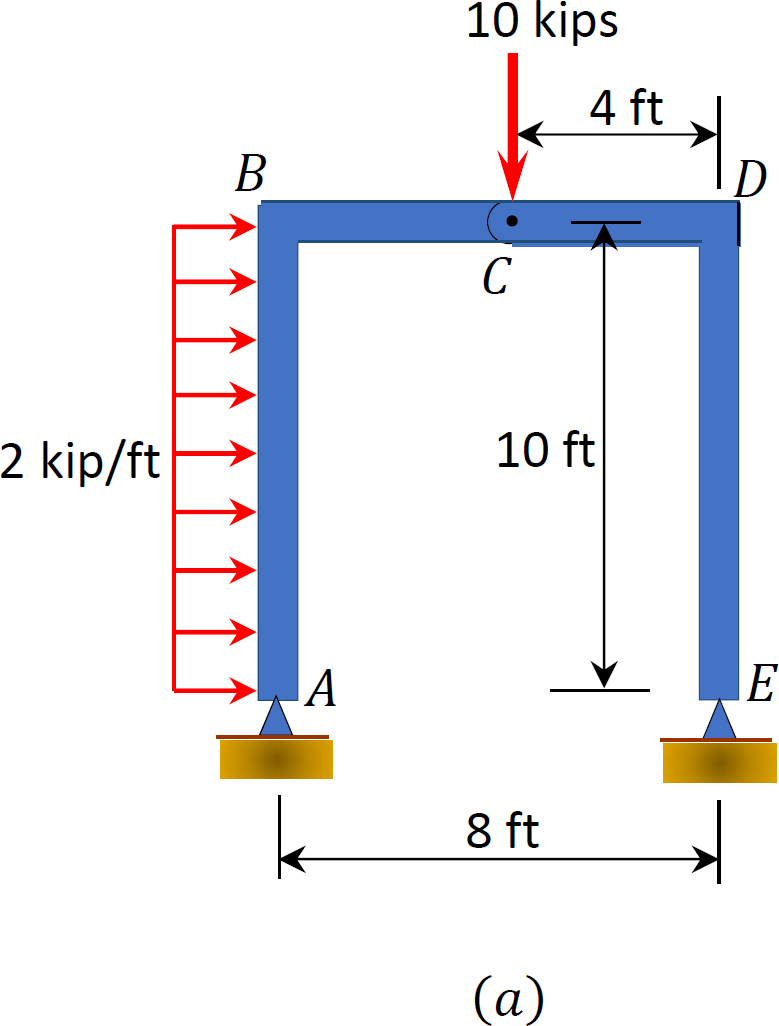
Solution
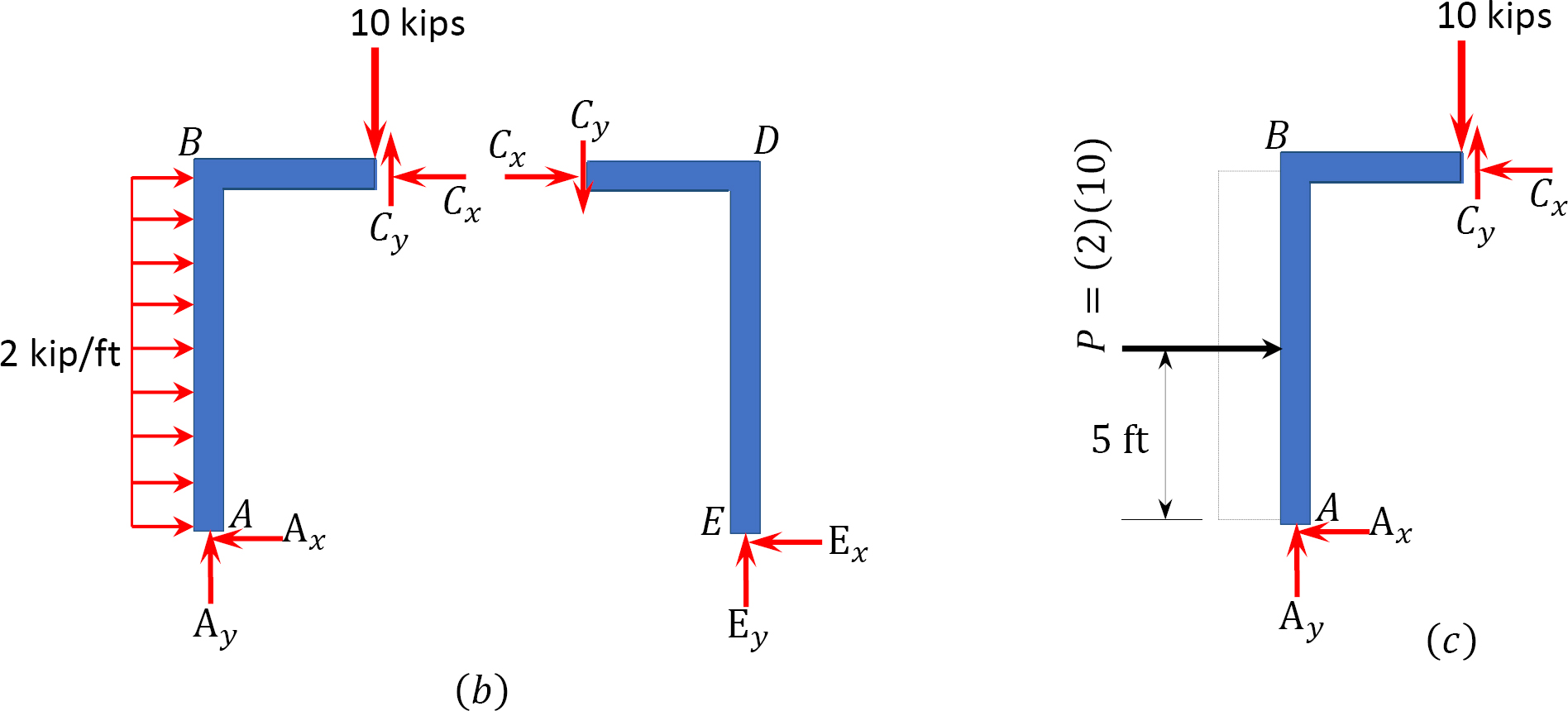
Free-body diagram. The free-body diagram of the frame is shown in Figure 3.20b.
Computation of reactions. The reactions in a compound frame are computed considering the freebody diagrams of both the entire frame and part of the frame. Prior to computation of the reactions, the distributed load in the column is replaced by a single resultant force. The vertical reactions at E and A and the horizontal reactions at A are found by applying the equations of static equilibrium and considering the free-body diagram of the entire frame. The horizontal reaction at E is found by considering part CDE of the free-body diagram.
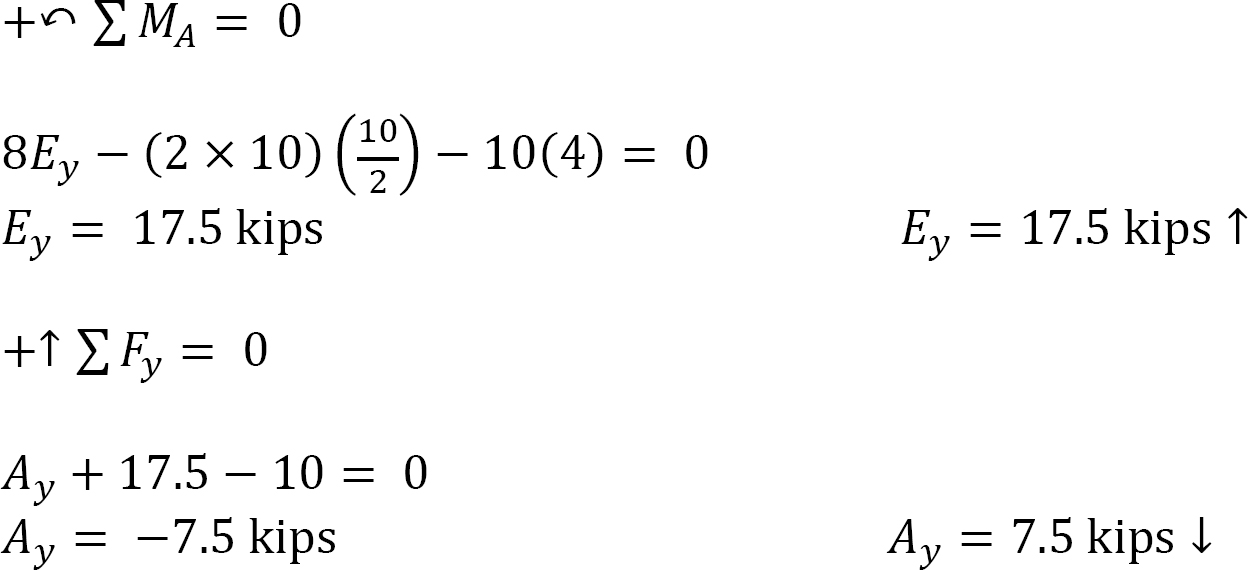
The negative sign implies that the originally assumed direction of Ay was not correct. Therefore, Ay acts downward instead of upward as was initially assumed. This should be corrected in the subsequent analysis.
To determine Ex, consider the moment of forces in member CDE about the hinge.


Example 3.15
Find the reactions at support A and B of the loaded frame in Figure 3.21a. The frame is hinged at D.
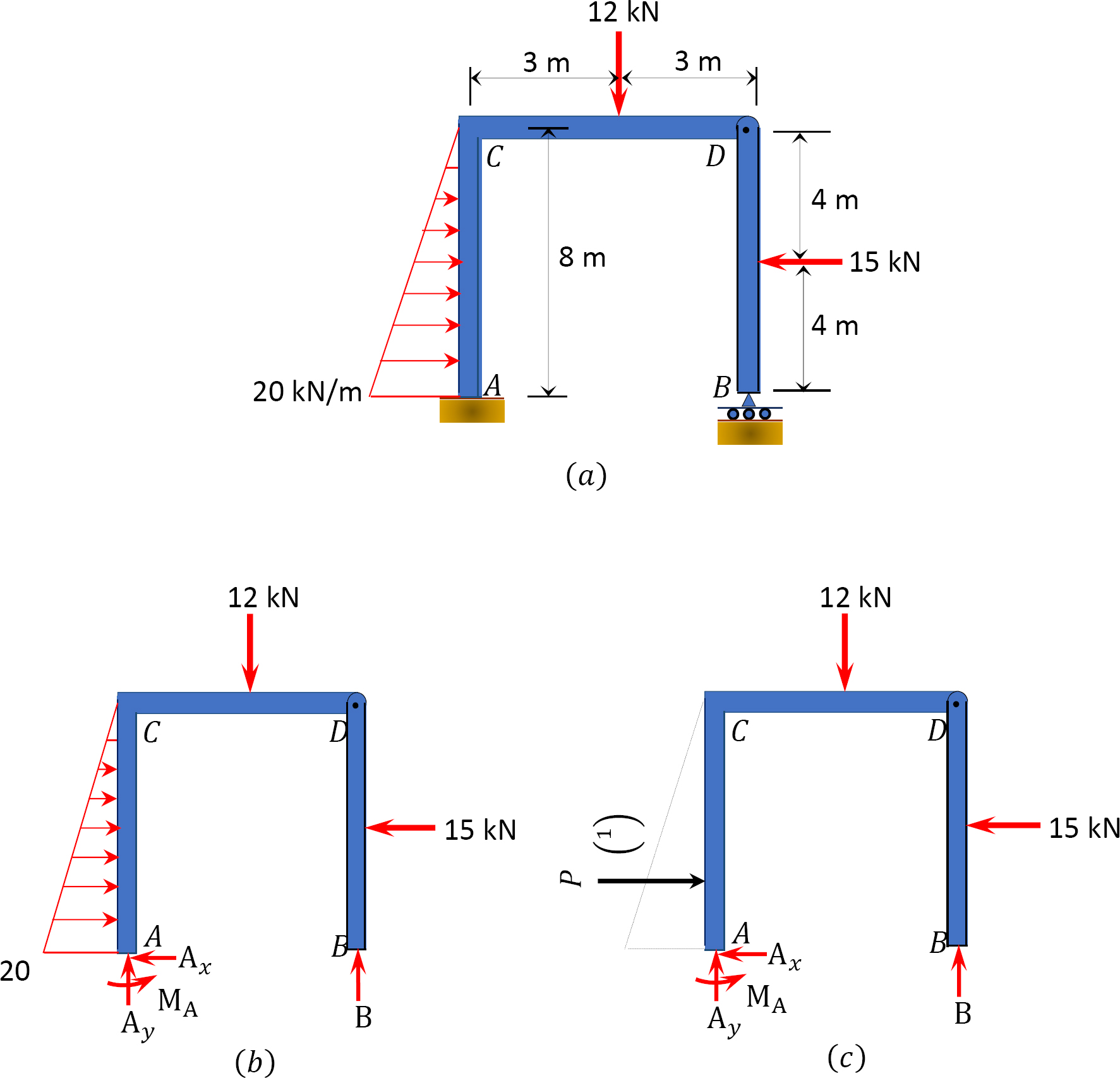
Solution
Free-body diagram. The free-body diagram of the frame is shown in Figure 3.21b.
Computation of reactions. The distributed load in column AC is first replaced with a single resultant force by finding the area of loading, as shown in Figure 3.21Figurec. The reaction at B is computed by taking the moment of the forces in part DB of the frame about the pin at D, and other reactions are determined by applying other conditions of equilibrium.

The negative sign implies that the originally assumed direction of Ay was not correct. Therefore, Ay acts downward instead of upward as was initially assumed. This should be corrected in the subsequent analysis.
Chapter Summary
Conditions of static equilibrium: A structure is in a state of static equilibrium if the resultant of all the forces and moments acting on it is equal to zero. Mathematically, this is expressed as follows:
∑ F = 0∑ M = 0
For a body in a plane, there are the following three equations of equilibrium:
∑ Fx = 0∑ Fy = 0∑ M0 = 0
Types of support: Various symbolic representations are used to model different types of supports for structures. A roller is used to model a support that prevents a vertical movement of a structure but allows a horizontal translation and rotation. A pin is used to model a support that prevents horizontal and vertical movements but allows rotation. A fixed support models a support that prevents horizontal and vertical movements and rotation.

Determinacy, indeterminacy, and stability of structures: A structure is determinate if the number of unknown reactions is equal to the number of static equilibrium. Thus, the equations of static equilibrium are enough for the determination of the supports for such a structure. On the other hand, a statically indeterminate structure is a structure that has the number of the unknown reactions in excess of the equations of equilibrium. For the analysis of an indeterminate structure additional equations are needed, and these equations can be obtained by considering the compatibility of the structure. Indeterminate structures are sometimes necessary when there is a need to reduce the sizes of members or to increase the stiffness of members. A stable structure is one which has support reactions that are not parallel or concurrent to one another. The formulation of stability and determinacy of beams and frames are as follows:
Beams and frames: |
3m + r < 3j + C Structure is unstable |
3m + r = 3j + C Structure is determinate |
|
3m + r > 3j + C Structure is indeterminate |
Practice Problems
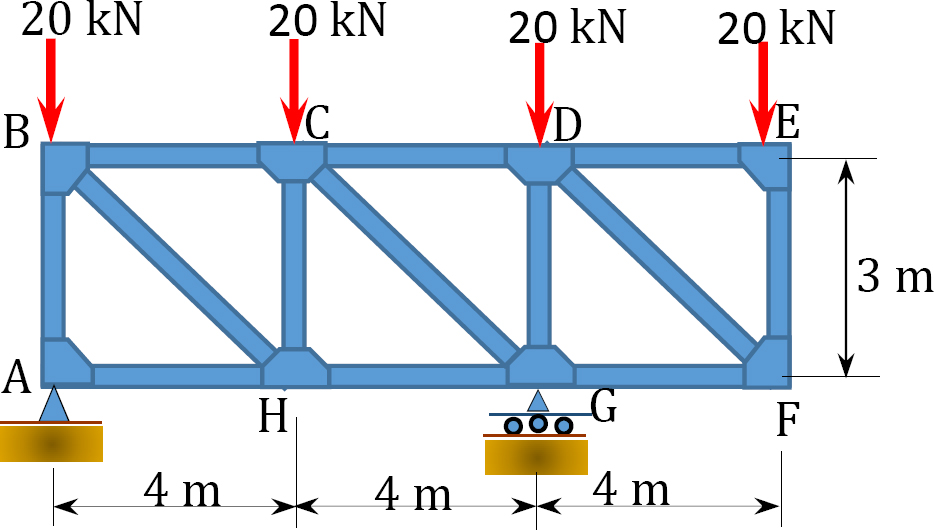
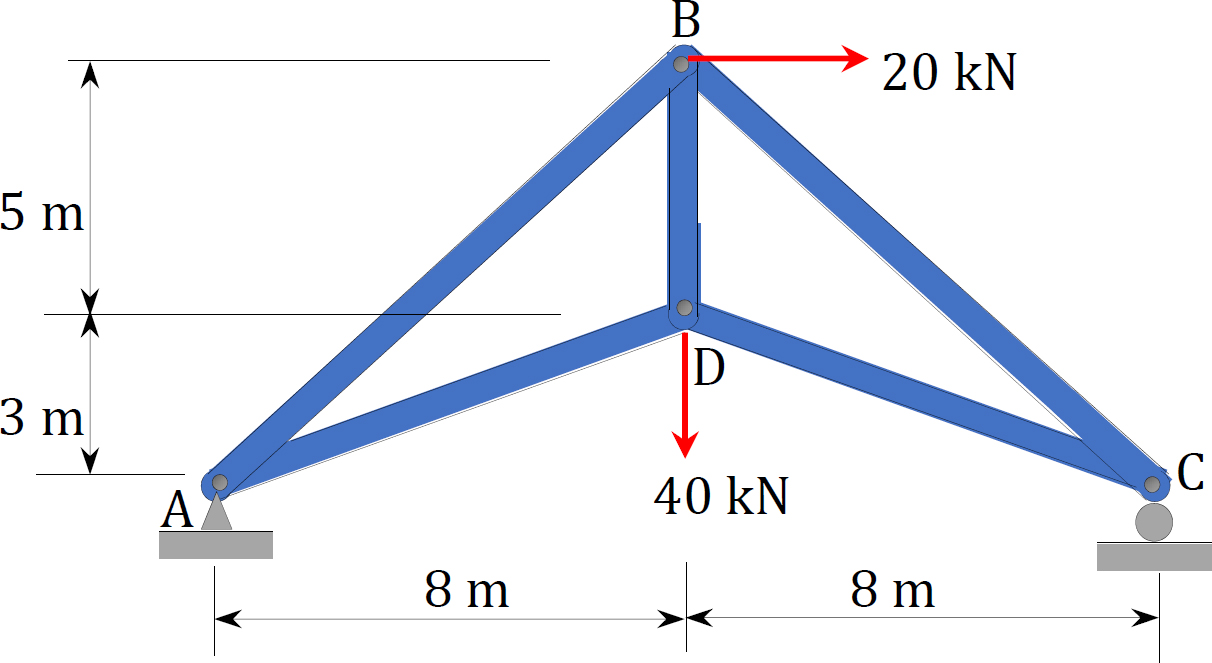
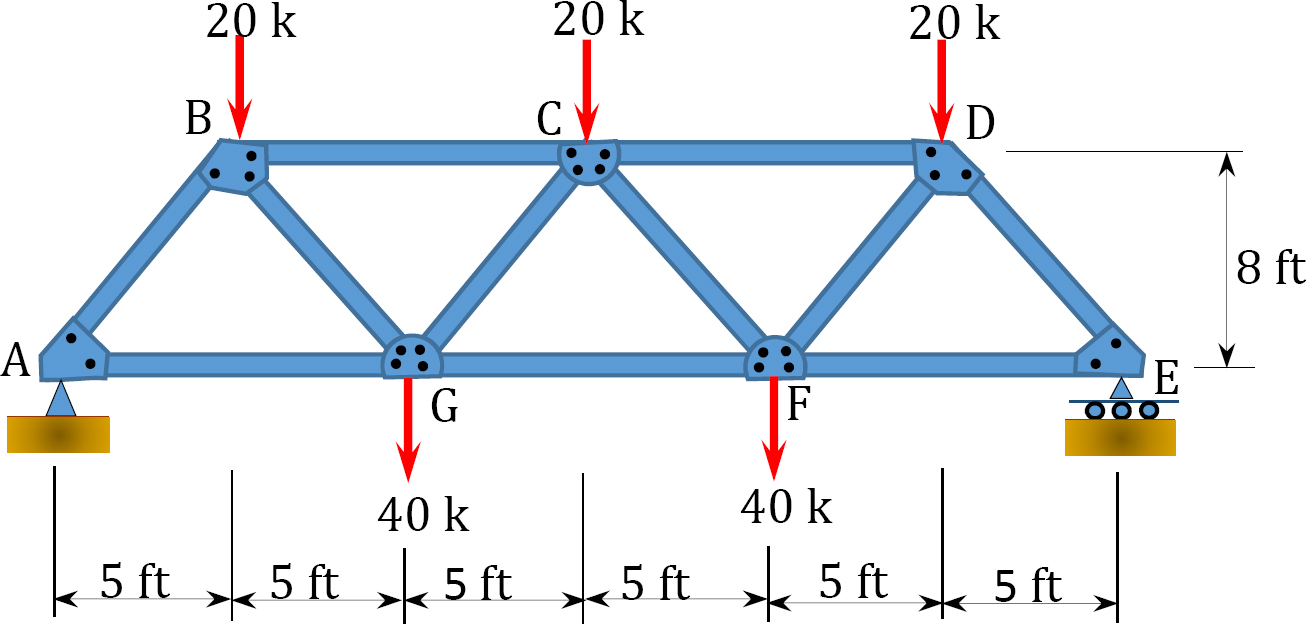
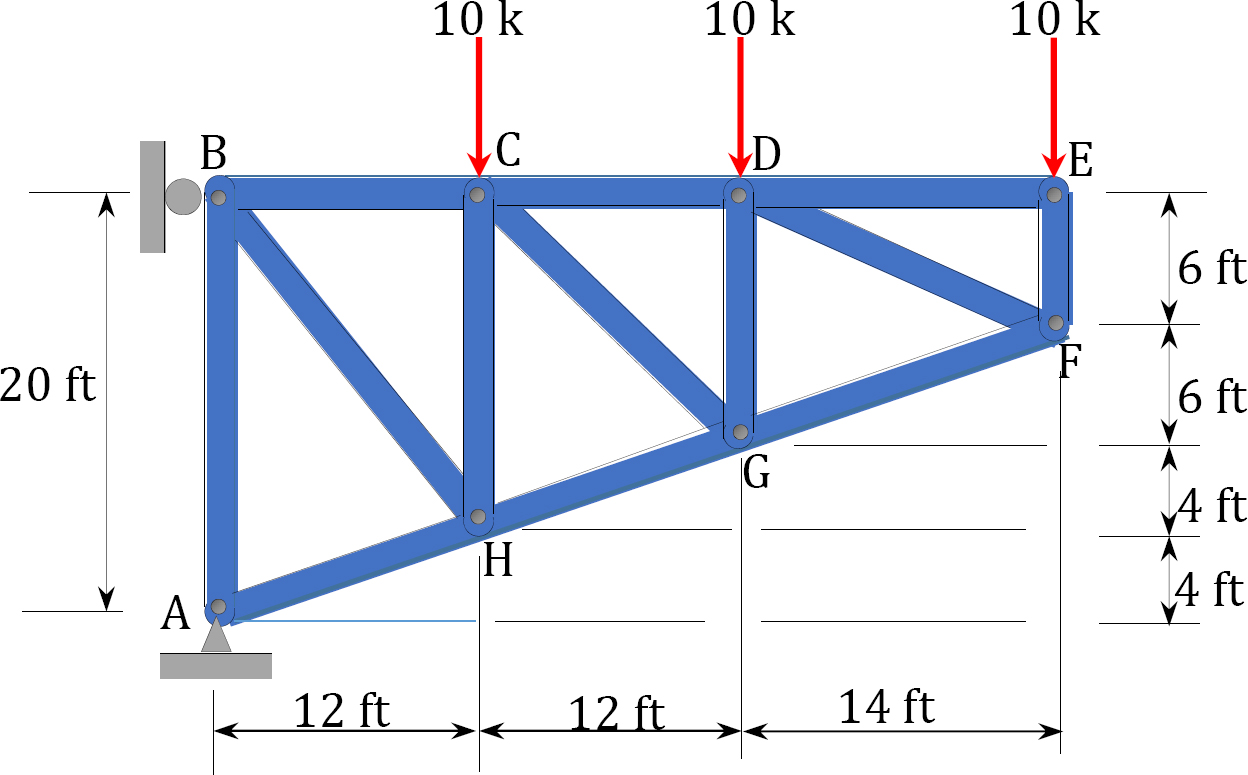
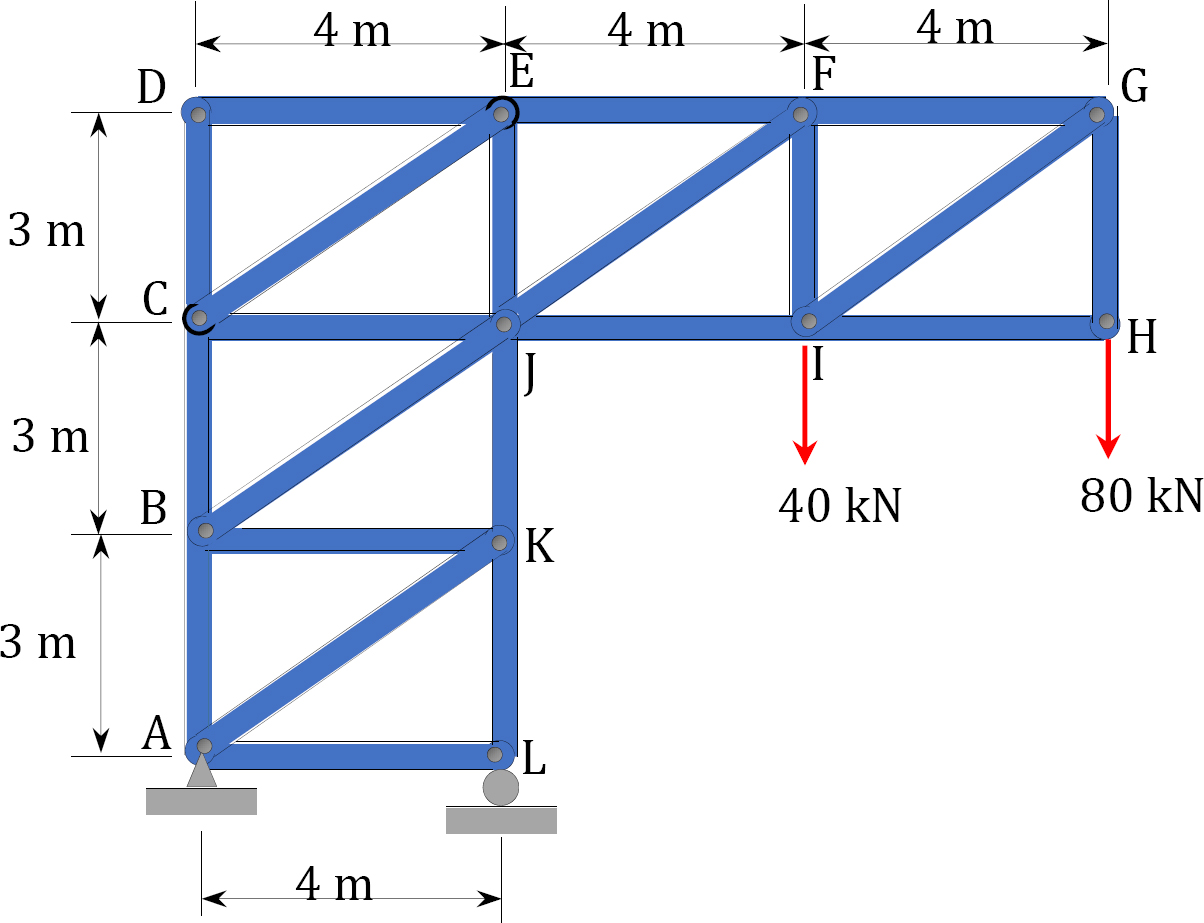
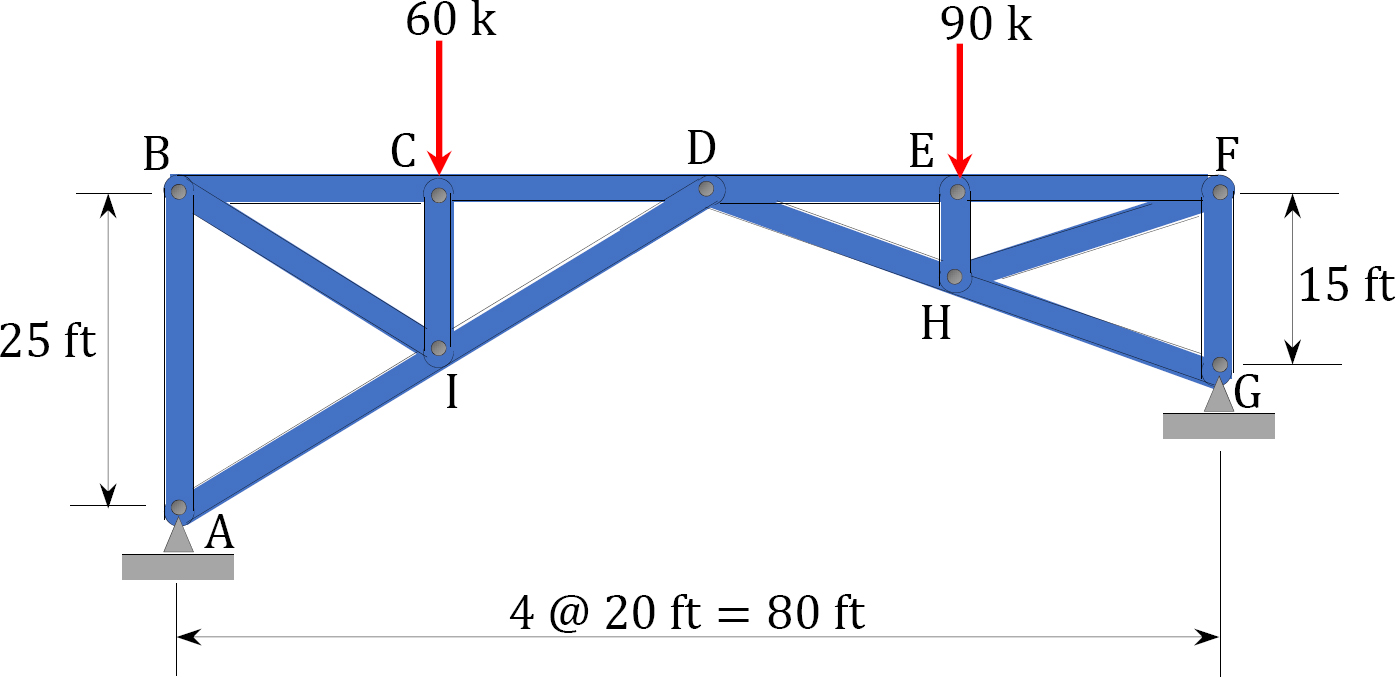
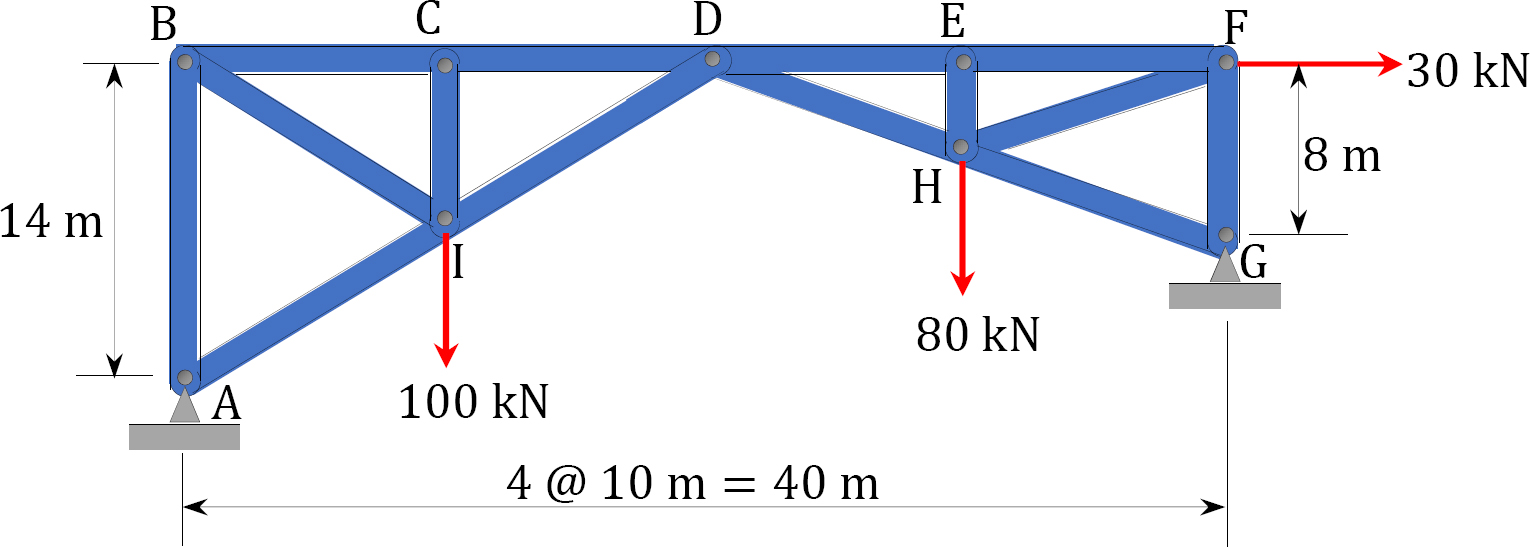
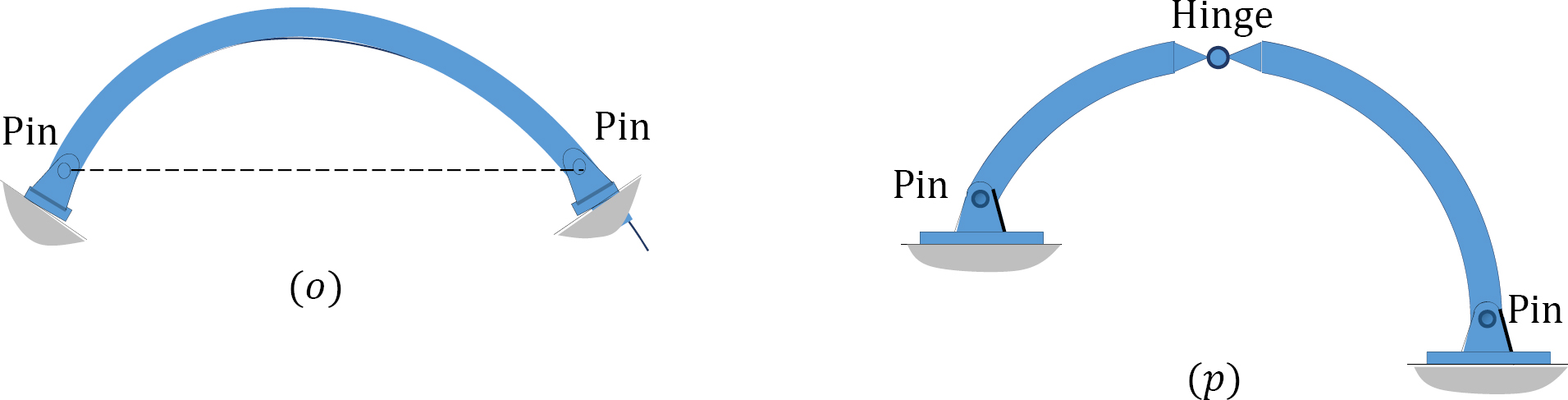
3.1 Classify the structures shown in Figure P3.1a to Figure P3.1p as statically determinate or indeterminate, and statically stable or unstable. If indeterminate, state the degree of indeterminacy.


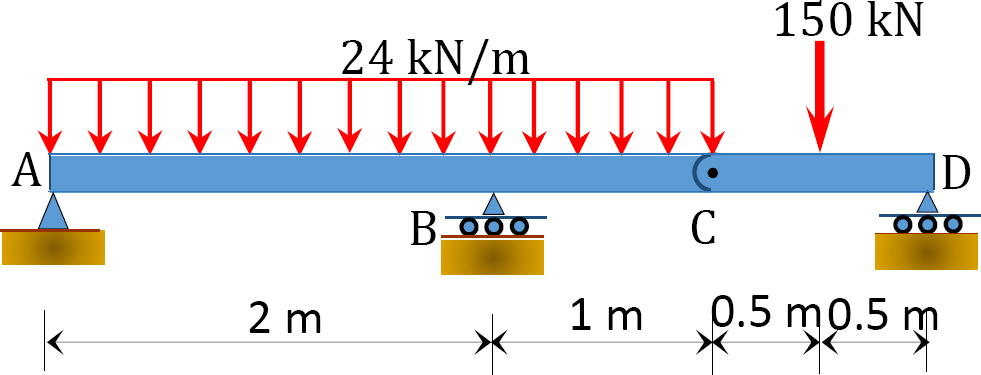
3.2. Determine the support reactions for the beams shown in Figure P3.2 through Figure P3.12.
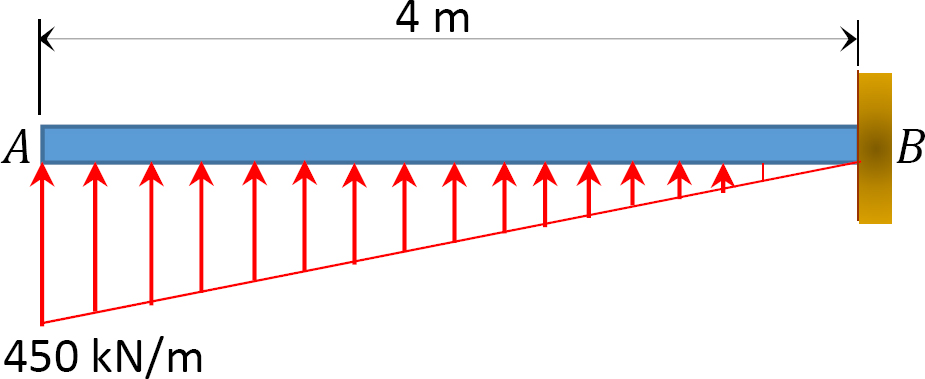
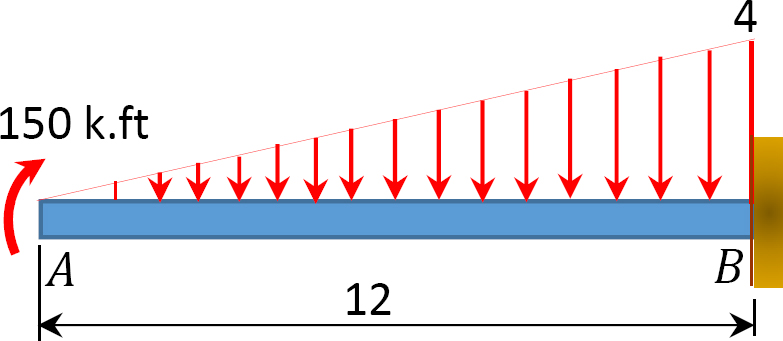

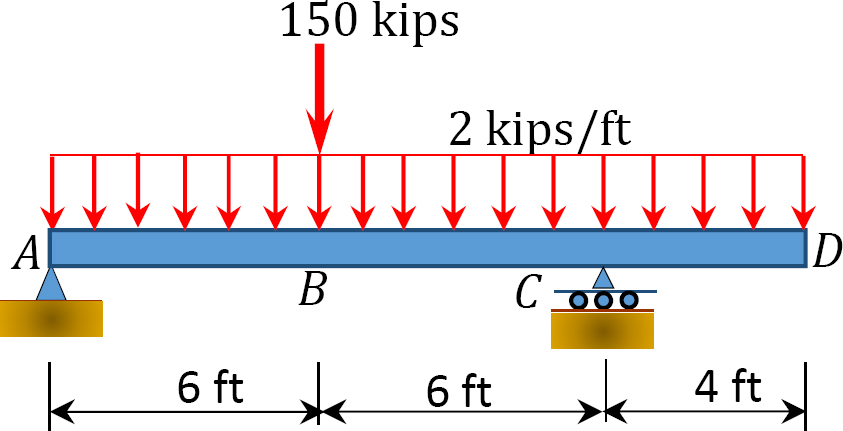
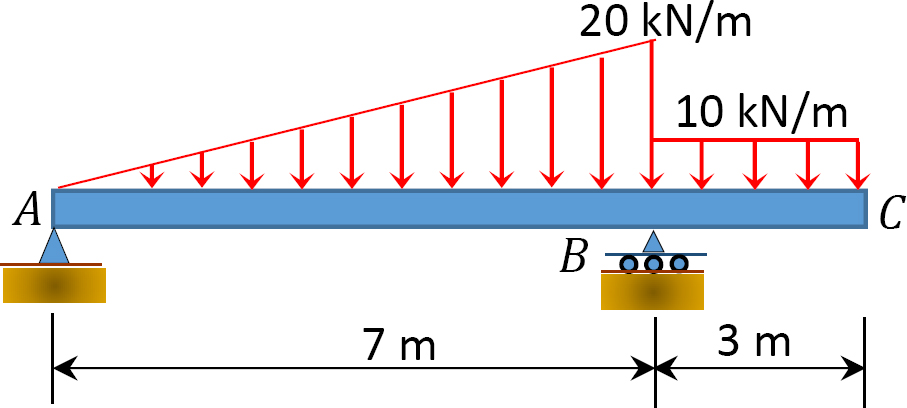
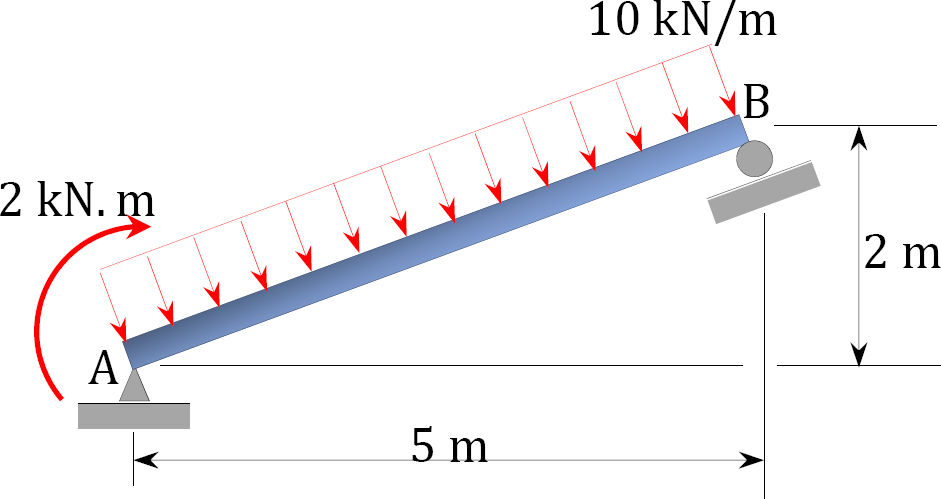
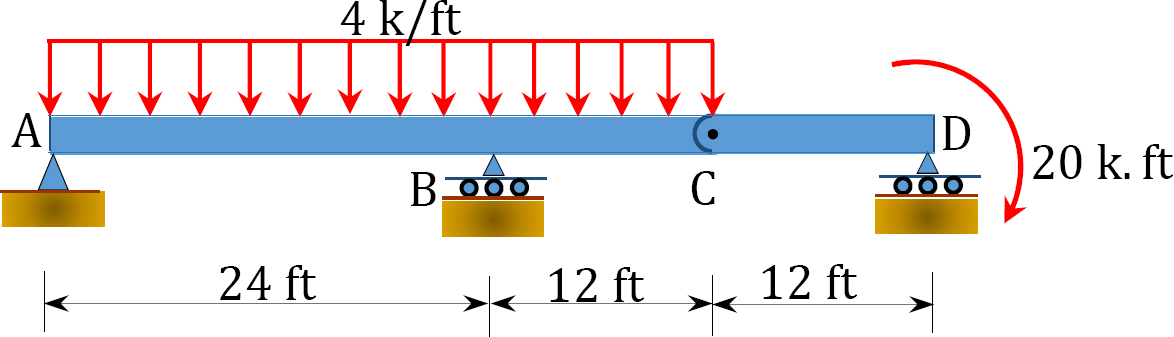
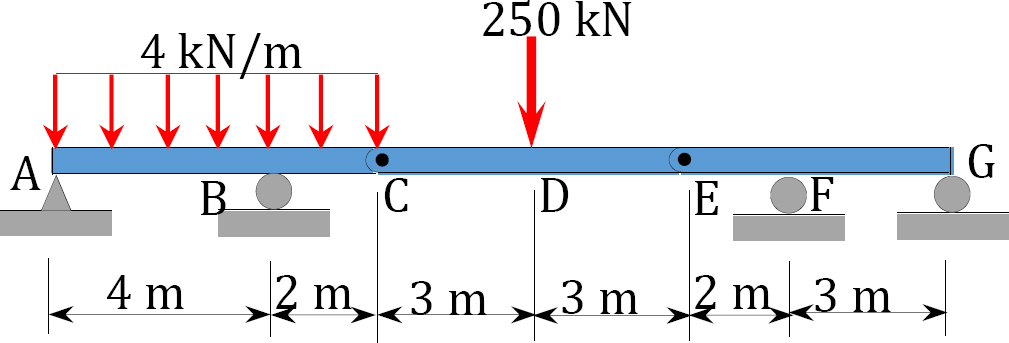
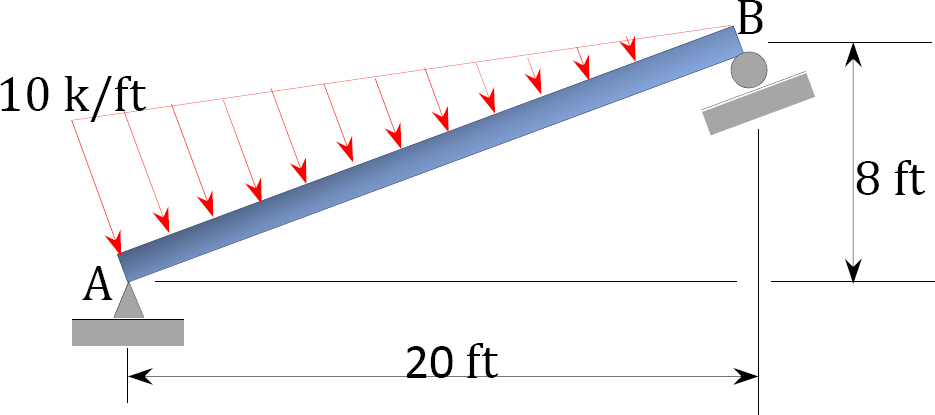
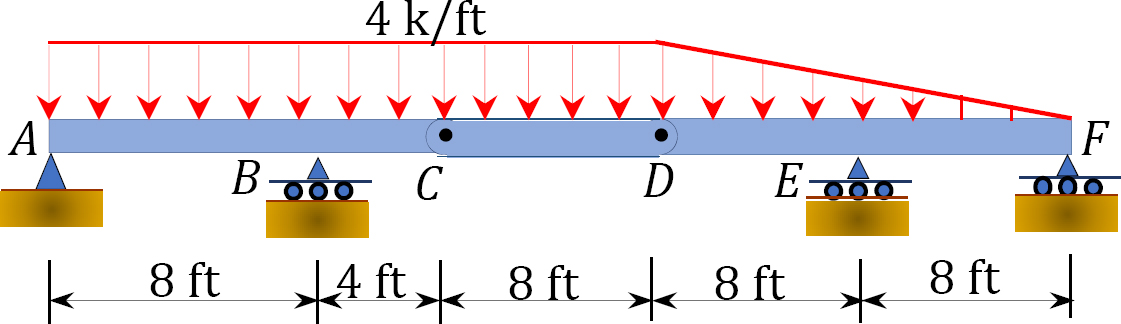
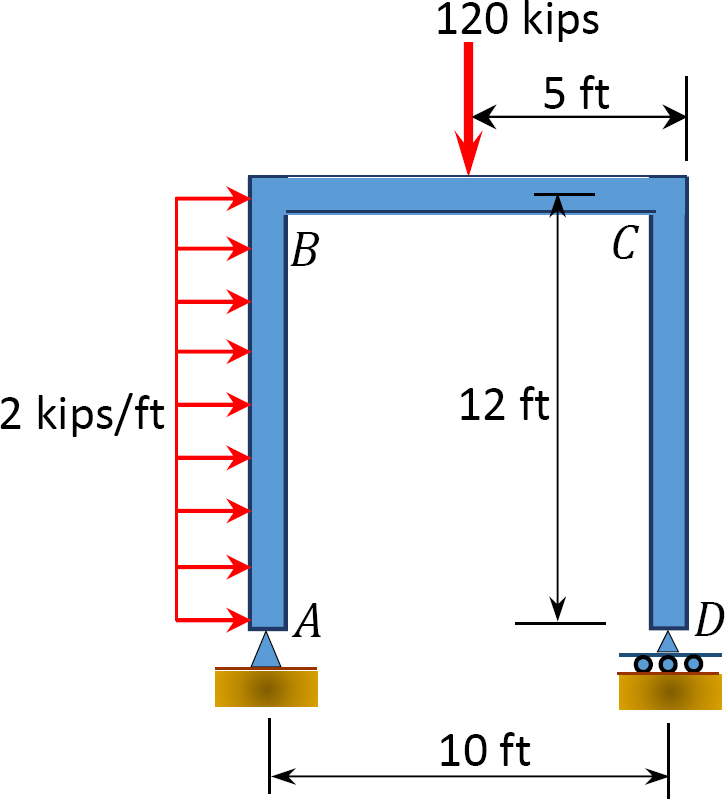
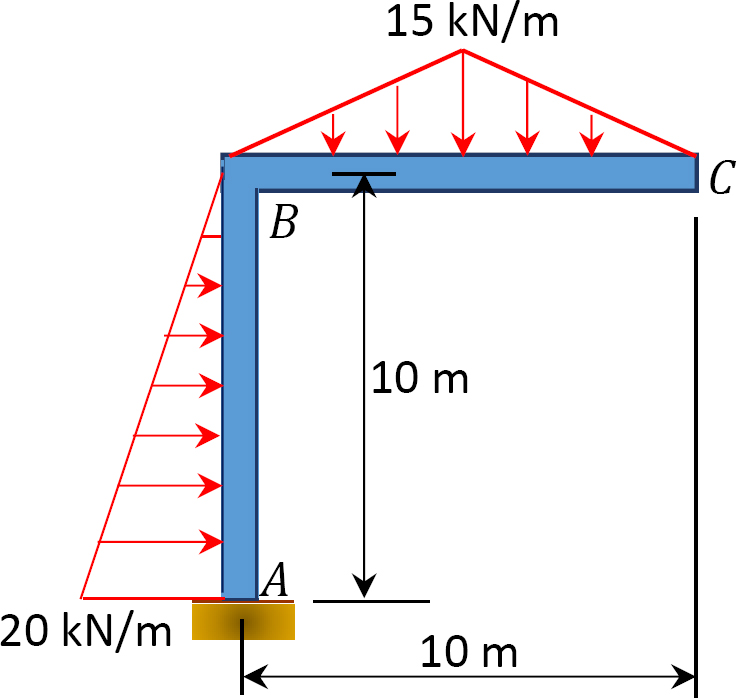
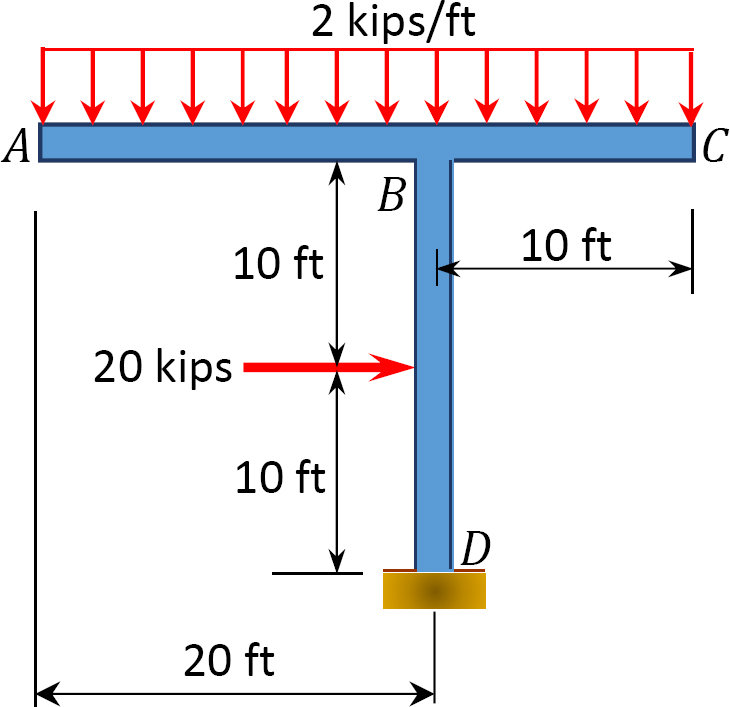
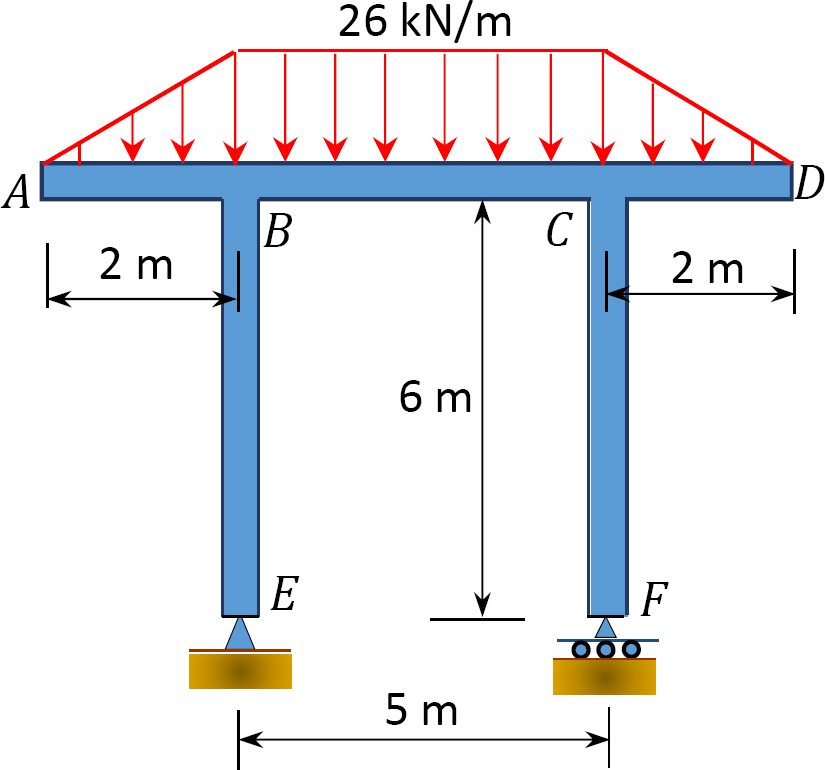
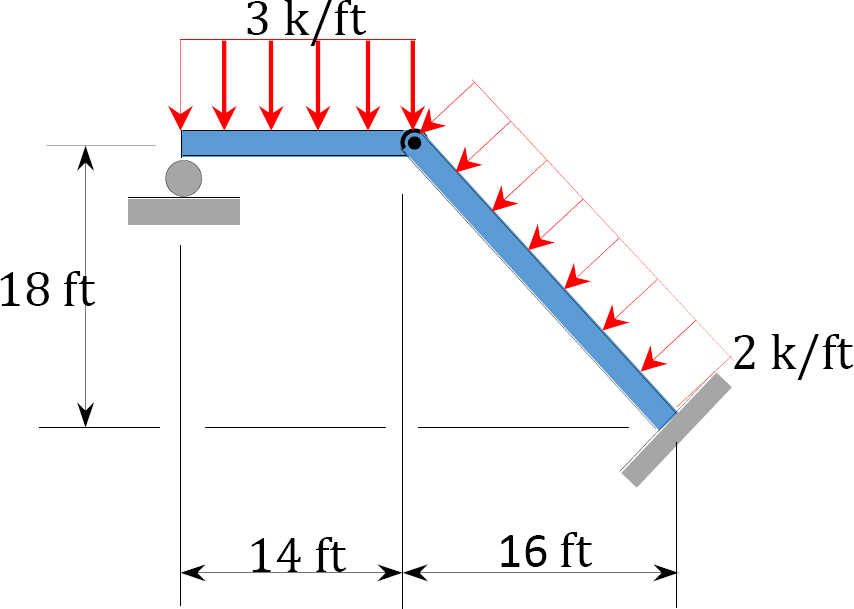
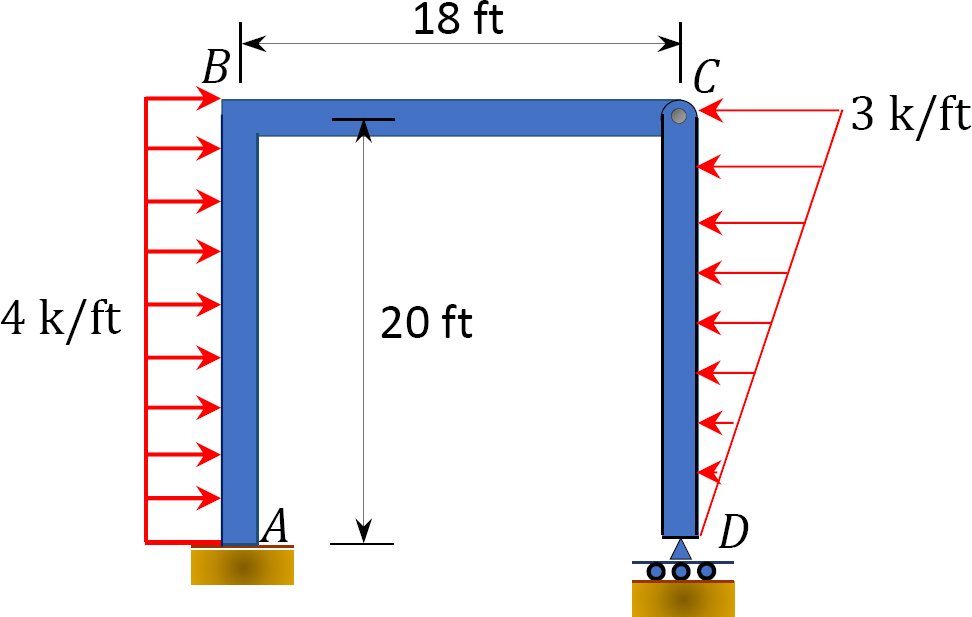
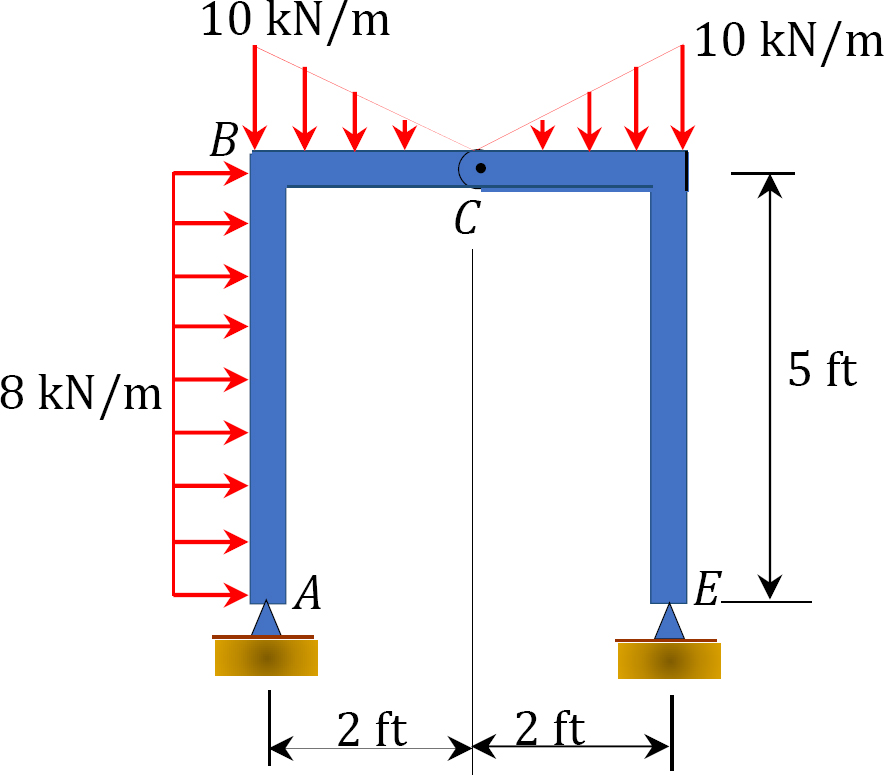
3.3. Determine the support reactions for the frames shown in Figure P3.13 through Figure P3.20.

3.4 Determine the support reactions for the trusses shown in Figure P3.21 through Figure P3.27.