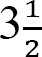1.2: Structural Loads and Loading System

Civil engineering structures are designed to sustain various types of loads and possible combinations of loads that could act on them during their lifetime. Accurate estimation of the magnitudes of these loads is a very important aspect of the structural analysis process. There are local and international codes, as well as research reports and documents, that aid designers in this regard. Structural loads can be broadly classified into four groups: dead loads, live loads, impact loads, and environmental loads. These loads are briefly described in the following sections.

2.1.1 Dead Loads

Dead loads are structural loads of a constant magnitude over time. They include the self-weight of structural members, such as walls, plasters, ceilings, floors, beams, columns, and roofs. Dead loads also include the loads of fixtures that are permanently attached to the structure. Prior to the analysis and design of structures, members are preliminarily sized based on architectural drawings and other relevant documents, and their weights are determined using the information available in most codes and other civil engineering literature. The recommended weight values of some commonly used materials for structural members are presented in Table 2.1. The determination of the dead load due to structural members is an iterative process. During design, member sizes and weight could change, and the process is repeated until a final member size is obtained that could support the member’s weight and the superimposed loads.

Table 2.1. Unit weights of construction materials.

Material	Unit Weight
	lb/ft^3	kN/m^3
Reinforced concrete Plain concrete Structural steel Aluminum Brick Concrete masonry unit Wood (Douglas fir larch) Engineered wood (plywood)	150 145 490 165 120 135 34 36
		23.60 22.60 77.00 25.90 18.90 21.20 5.30 5.7

Example \(\PageIndex{1}\)

The semi-gravity retaining wall shown in Figure 2.1 Figure 2.1 is made of mass concrete with a unit weight of 23.6 kN/m³. Determine the length of the wall’s weight per foot.

Fig. 2.1. Semi – gravity retaining wall (all dimensions in cm).

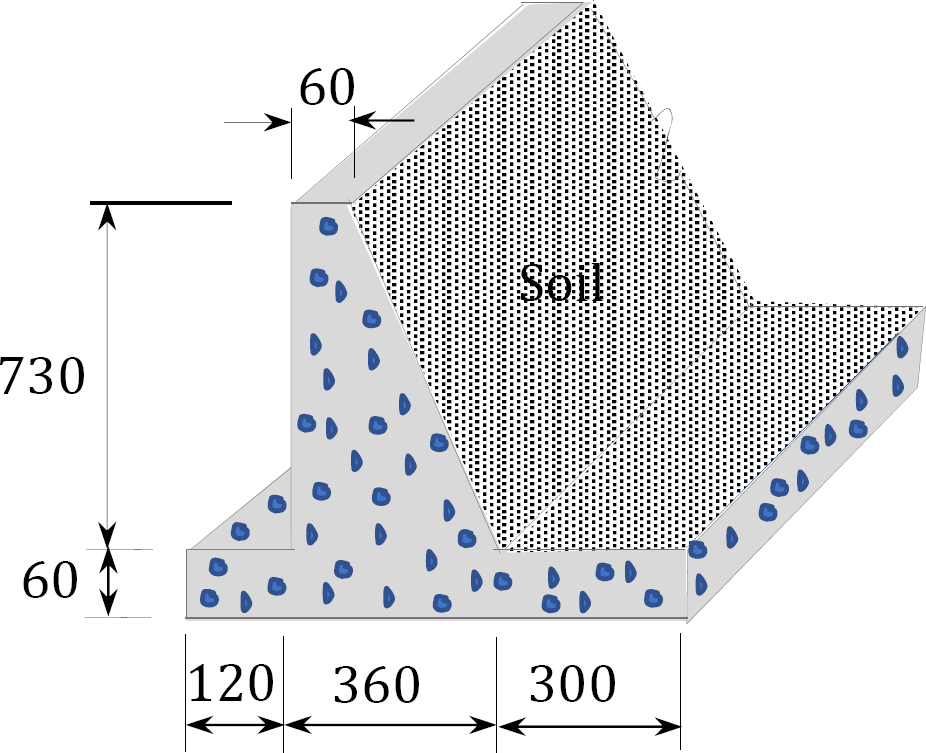
Solution

Area of wall = (7.8 m)(0.6 m) + (7.3 m)(0.6 m) + (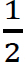)(3 m)(7.3 m) = 20.01 m²

Length of the wall’s weight per foot = 20.01 m² × (23.6 kN/m³) = 472.24 kN/m

2.1.2 Live Loads

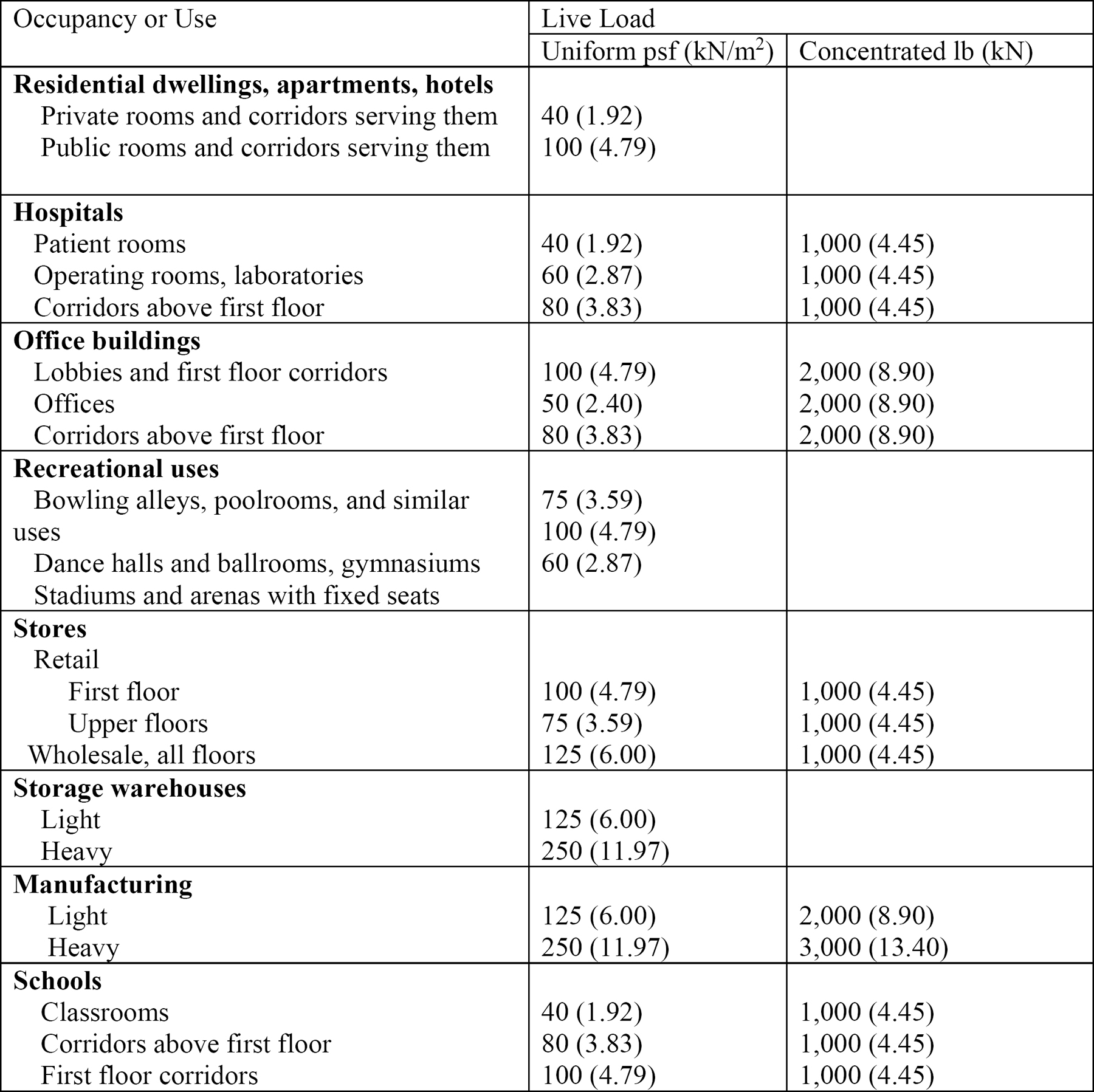
Live loads are moveable or temporarily attached to a structure. They include the loads on a building created by the storage of furniture and equipment, occupancy (people), and impact. Typical live load values are presented in Table 2.2. The loads were obtained from Table 4.3-1 in ASCE 7-16.

Table 2.2. Minimum uniform and concentrated floor live loads.

Example \(\PageIndex{1}\)

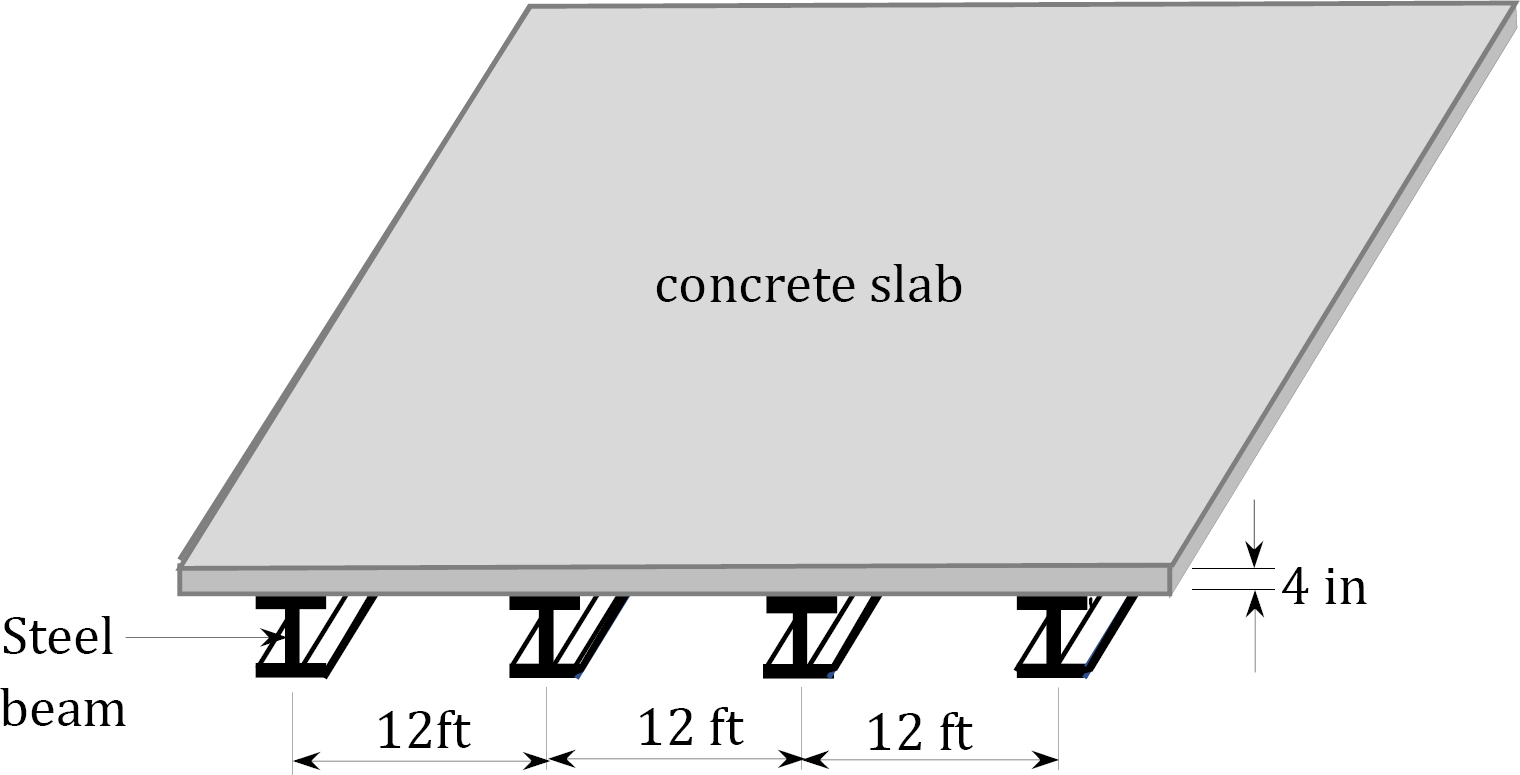
The floor system of the classroom shown in Figure 2.2 consists of a 3-inch-thick reinforced concrete slab supported by steel beams. If the weight of each steel beam is 62 lb/ft, determine the dead load in lb/ft supported by any interior beam.

Fig. 2.2. Classroom floor system.

Solution

Dead load due to slab weight =

Dead load due to beam weight = 62 lb/ft

Live load due to occupancy or use (classroom) = (40 lb/ft²)(12 ft) = 480 lb/ft

Total uniform load on steel beam = 1142 lb/ft = 1.142 k/ft

2.1.3 Impact Loads

Impact loads are sudden or rapid loads applied on a structure over a relatively short period of time compared with other structural loads. They cause larger stresses in structural members than those produced by gradually applied loads of the same magnitude. Examples of impact loads are loads from moving vehicles, vibrating machinery, or dropped weights. In practice, impact loads are considered equal to imposed loads that are incremented by some percentage, called the impact factor. Some building load impact factors are presented in Table 2.3. The American Association of State Highway and Transportation Officials (AASHTO) specifies the following expression for the computation of the impact factor for a moving truck load for use in highway bridge design:

where

• I = impact factor.
• L = length in feet (or meters) of the span-loaded segment to cause maximum stress in the member under consideration.

Table 2.3. Building live load impact factors, as specified in ASCE/SEI 7-16.

Loading Case	I(%)
Elevator supports and machinery Light machinery supports Reciprocating machine supports Hangers supporting floors and balconies Crane support girders and their connections	100 20 50 33 25

2.1.4 Environmental Loads

2.1.4.1 Rain Loads

Rain loads are loads due to the accumulated mass of water on a rooftop during a rainstorm or major precipitation. This process, which is referred to as ponding, mostly occurs in flat roofs and roofs with pitches of less than 0.25 in/feet. Ponding in roofs occurs when the run off after precipitation is less than the amount of water retained on the roof. Water accumulated on a flat or low-pitch roof during a rainstorm can create a major structural load. Therefore, it must be considered when designing a building. The International Code Council requires that roofs with parapets include primary and secondary drains. The primary drain collects water from the roof and directs it to the sewer, while the secondary drain serves as a backup in the event that the primary drain is clogged. Figure 2.3 depicts a roof and these drainage systems. Section 8.3 of ASCE7-16 specifies the following equation for the computation of rain loads on an undeflected roof in the event that the primary drain is blocked:

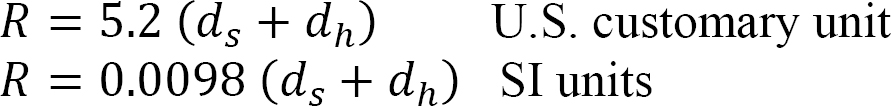
where

• R = rain load on the undeflected roof, in psi or KN/m².
• d_s = depth of water on the undeflected roof up to the inlet of the secondary drainage system (i.e. the static head), in inches or mm.
• d_h = additional depth of water on the undeflected roof above the inlet of the secondary drainage system (i.e. the hydraulic head), in inches or mm. It depends on the flow rate, the size of the drainage, and the area drained by each drain.

The flow rate, Q, in gallons per minute, can be computed as follows:

Q (gpm) = 0.0104 Ai

where

• A = roof area in square feet drained by the drainage system.
• i = 100-yr., 1-hr. rainfall intensity in inches per hour for the building location specified in the plumbing code.

Fig. 2.3. Roof drainage system (Adapted from the International Code Council).

2.1.4.2 Wind Loads

Wind loads are pressures exacted on structures by wind flow. Wind forces have been the cause of many structural failures in history, especially in coastal regions. The speed and direction of wind flow varies continuously, making it difficult to predict the exact pressure applied by wind on existing structures. This explains the reason for the considerable research efforts on the effect and estimation of wind forces. Figure 2.4 shows a typical wind load distribution on a structure. Based on Bernoulli’s principle, the relationship between dynamic wind pressure and wind velocity can be expressed as follows when visualizing the flow of wind as that of a fluid:

where

• q = dynamic wind pressure air in pounds per square foot.
• ρ = mass density of air.
• V = wind velocity in miles per hour.

Basic wind speed for specific locations in the continental United States can be obtained from the basic speed contour map in ASCE 7-16.

Assuming that the unit weight of air for a standard atmosphere is 0.07651 lb/ft³ and substituting this value into the previously stated equation 2.1, the following equation can be used for static wind pressure:

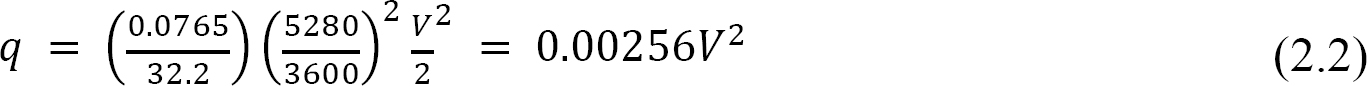
To determine the magnitude of wind velocity and its pressure at various elevations above ground level, the ASCE 7-16 modified equation 2.2 by introducing some factors to account for the height of the structure above ground level, the importance of the structure in regard to human life and property, and the topography of its location, as follows:

where

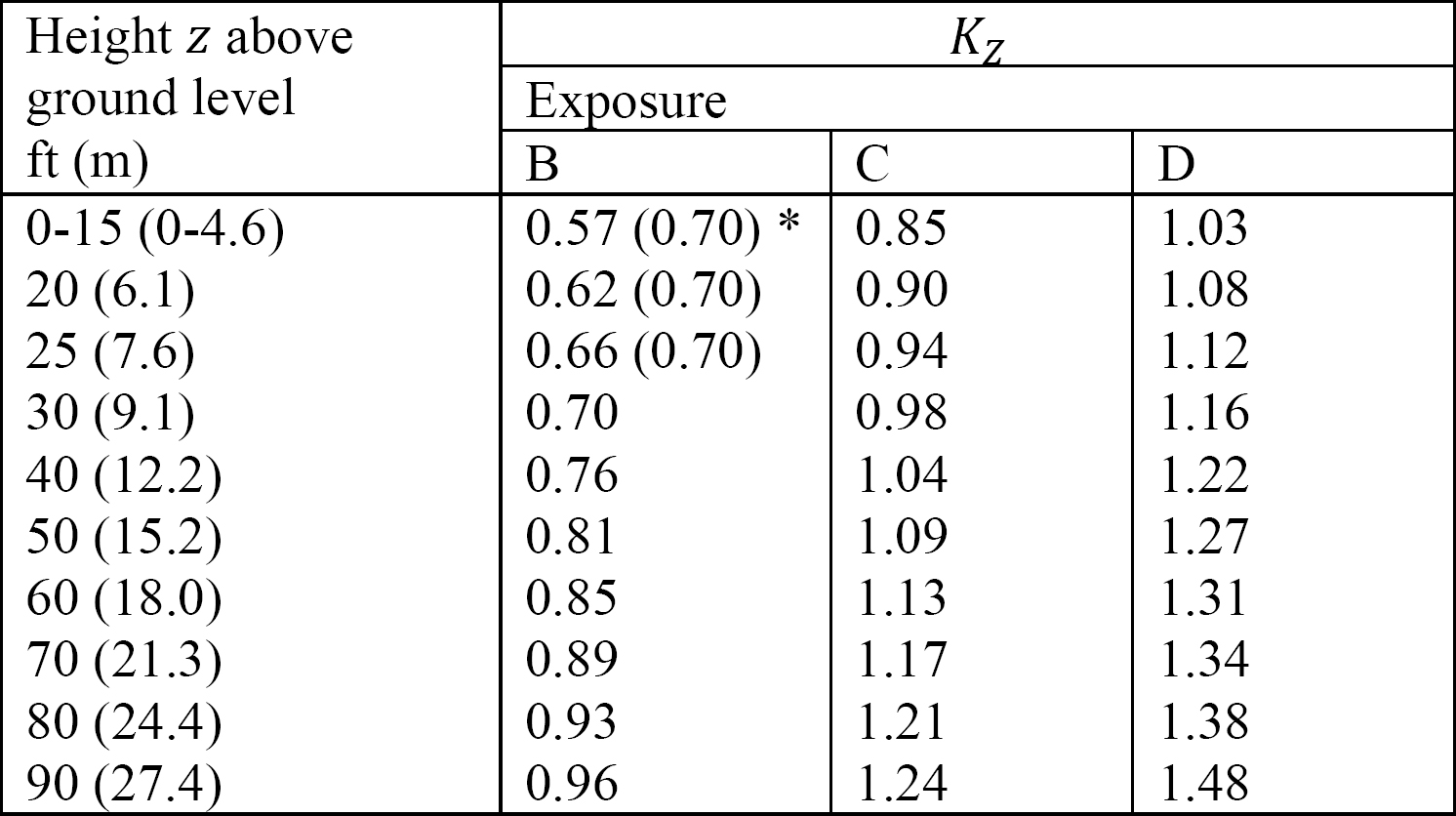
K_z = the velocity pressure coefficient that depends on the height of the structure and the exposure condition. The values of K_z are listed in Table 2.4.

K_zt = a topographic factor that accounts for an increase in wind velocity due to sudden changes in topography where there are hills and escarpments. This factor is an equal unity for building on level ground and increases with elevation.

K_d = wind directionality factor. It accounts for the reduced probability of maximum wind coming from any given direction and for the reduced probability of the maximum pressure developing on any wind direction most unfavorable to the structure. For structures subjected to wind loads only, K_d = 1; for structures subjected to other loads, in addition to a wind load, K_d values are tabulated in Table 2.5.

• K_e = ground elevation factor. According to section 26.9 in ASCE 7-16, it is expressed as K_e = 1 for all elevations.
• V = velocity of wind measured at a height z above ground level.

The three exposure conditions categorized as B, C, and D in Table 2.4 are defined in terms of surface roughness, as follows:

Exposure B: The surface roughness for this category includes urban and suburban areas, wooden areas, or other terrain with closely spaced obstructions. This category applies to buildings with mean roof heights of ≤ 30 ft (9.1 m) if the surface extends in the upwind direction for a distance greater than 1,500 ft. For buildings with mean roof heights greater than 30 ft (9.1 m), this category will apply if the surface roughness in the upwind direction is greater than 2,600 ft (792 m) or 20 times the height of the building, whichever is greater.

Exposure C: Exposure C applies where surface roughness C prevails. Surface roughness C includes open terrain with scattered obstructions having heights less than 30 ft.

Exposure D: The surface roughness for this category includes flats, smooth mud flats, salt flats, unbroken ice, unobstructed areas, and water surfaces. Exposure D applies where surface roughness D extends in the upwind direction for a distance greater than 5,000 ft or 20 times the building height, whichever is greater. This also applies if the surface roughness upwind is B or C, and the site is within 600 ft (183 m) or 20 times the building height, whichever is greater.

Table 2.4. Velocity pressure exposure coefficient, K_z, as specified in ASCE 7-16.

Table 2.5. Wind directional factor, K_d, as specified in ASCE 7-16.

Structure Type	Kd
Main wind force resisting system (MWFRS) Components and cladding	0.85 0.85
Arched roofs	0.85
Chimneys, tanks, and similar structures Square Hexagonal Round	0.9 0.95 0.95
Solid freestanding walls and solid freestanding and attached signs	0.85
Open signs and lattice framework	0.85
Trussed towers Triangular, square, rectangular All other cross sections	0.85 0.95

To obtain the final external pressures for the design of structures, equation 2.3 is further modified, as follows:

where

• P_z = design wind pressure on a face of the structure at height z above ground level. It increases with the height on the windward wall, but it is constant with the height on the leeward and side walls.
• G = gust effect factor. G = 0.85 for rigid structures with a natural frequency of ≥ 1 Hz. The gust factors for flexible structures are calculated using the equations in ASCE 7-16.
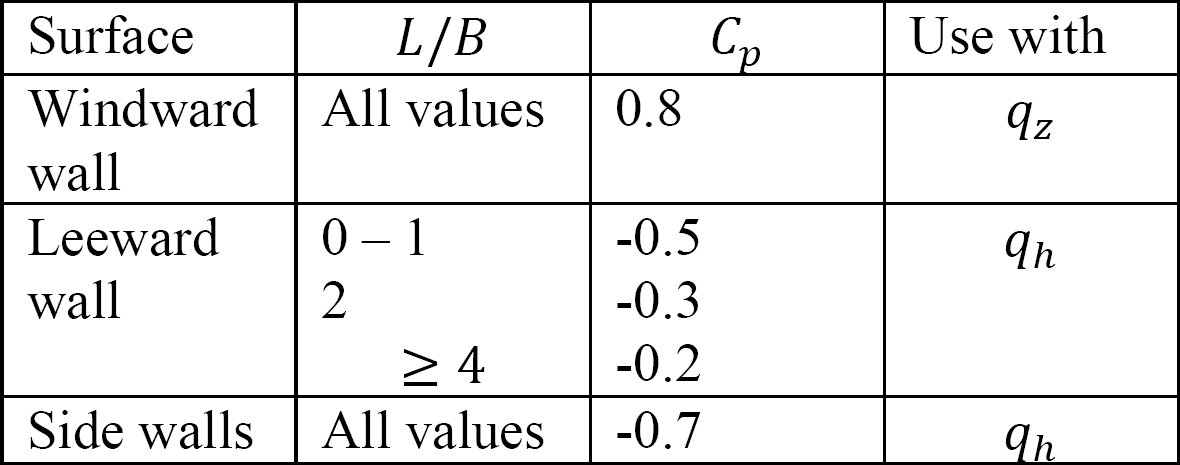
• C_p = external pressure coefficient. It is a fraction of the external pressure on the windward walls, leeward walls, side walls, and roof. The values of C_p are presented in Tables 2.6 and 2.7.

To compute the wind load that will be used for member design, combine the external and internal wind pressures, as follows:

where

GC_pi = the internal pressure coefficient from ASCE 7-16.

Fig. 2.4. Typical wind distribution on a structureus walls and roof.

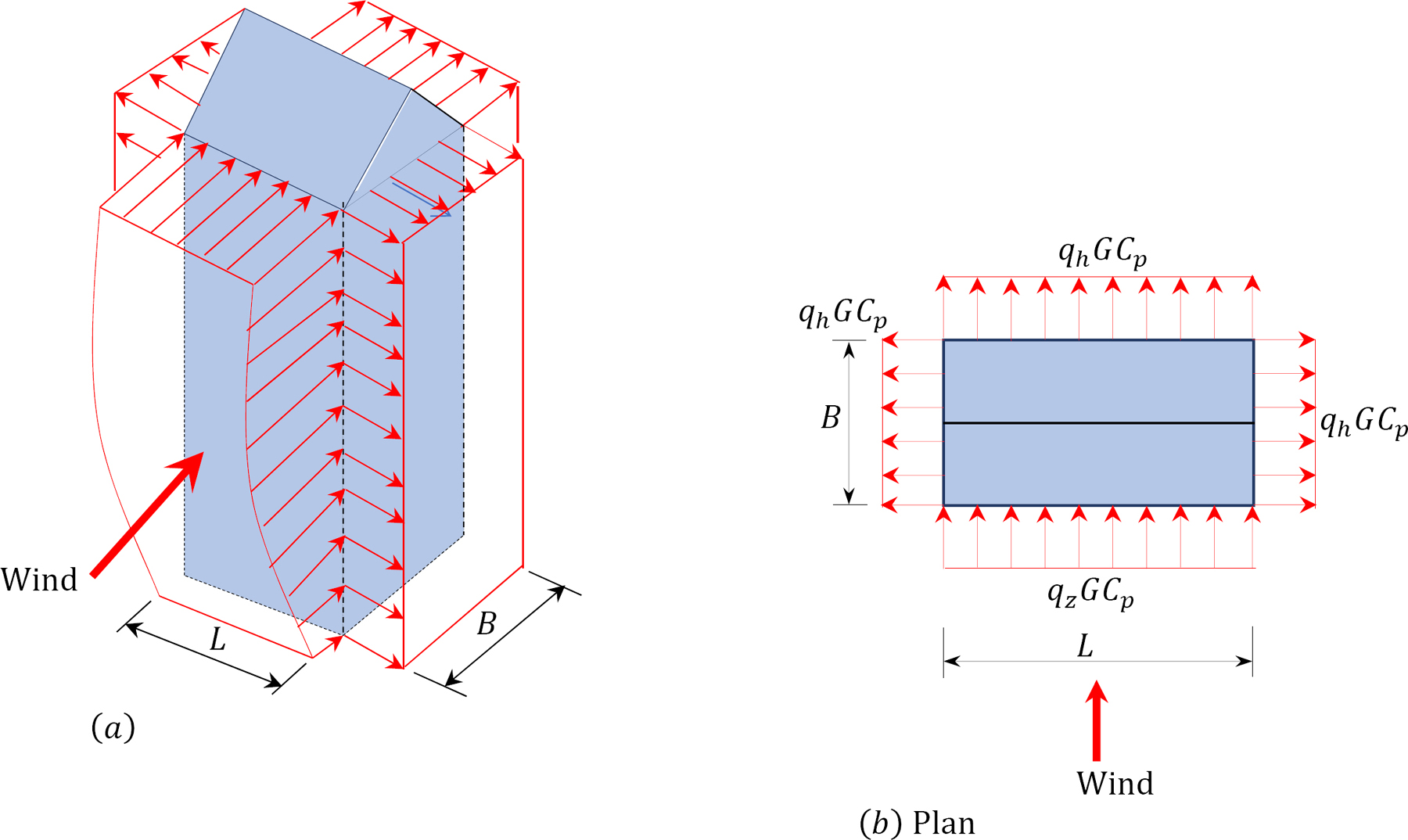
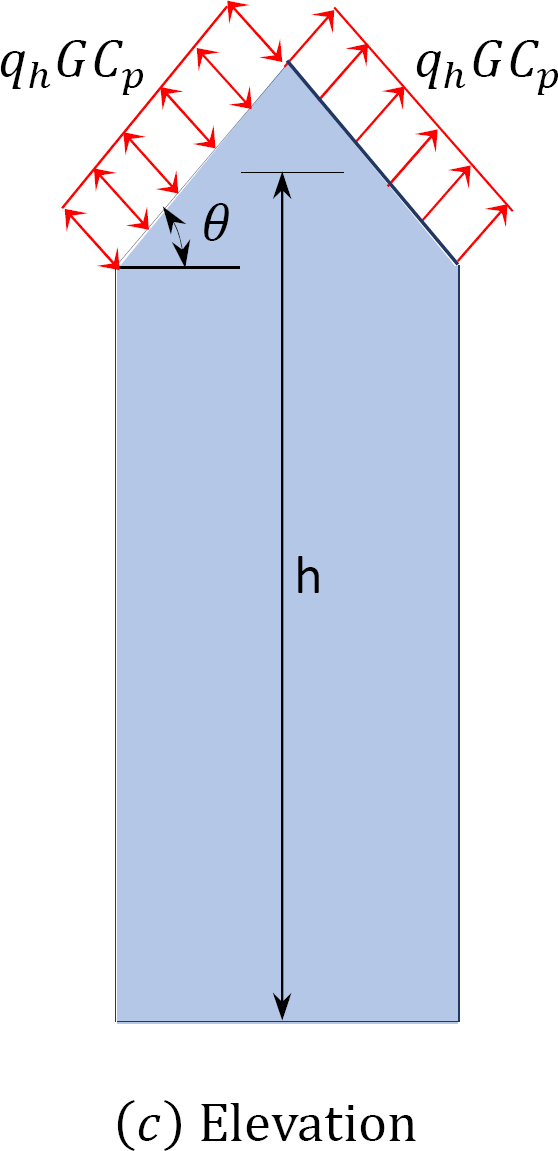
Table 2.6. Wall pressure coefficient, C_p, as specified in ASCE 7-16.

Notes:

1.Positive and negative signs are indicative of the wind pressures acting toward and away from the surfaces.

2.L is the dimension of the building normal to the wind direction, and B is the dimension parallel to the wind direction.

Table 2.7. Roof pressure coefficients, C_p, for use with q_h, as specified in ASCE 7-16.

Example \(\PageIndex{1}\)

The two-story building shown in Figure 2.5 is an elementary school located on a flat terrain in a suburban area, with a wind speed of 102 mph and exposure category B. What is the wind velocity pressure at roof height for the main wind force resisting system (MWFRS)?

Fig. 2.5. Two – story building.

Solution

The mean height of the roof is h = 20 ft.

Table 26.10-1 from ASCE 7-16 states that if the exposure category is B and the velocity pressure exposure coefficient for h= 20′, then K_z = 0.7.

The topography factor from section 26.8.2 of ASCE 7-16 is K_zt = 1.0.

The wind directionality factor for MWFRS, according to Table 26.6-1 in ASCE 7-16, is K_d = 0.85.

Using equation 2.3, the velocity pressure at a roof height of 20′ for the MWFRS is as follows:

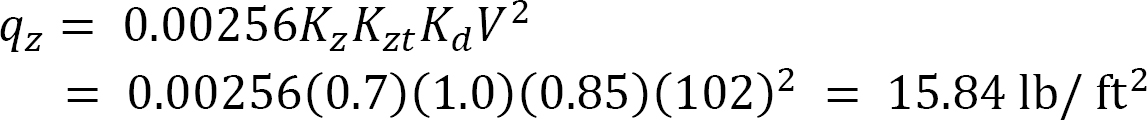
2.1.4.3 Snow Loads

In some geographic regions, the force exerted by accumulated snow and ice on buildings’ roofs can be quite enormous, and it can lead to structural failure if not considered in structural design.

Suggested design values of snow loads are provided in codes and design specifications. The basis for the computation of snow loads is what is referred to as the ground snow load. The ground snow load is defined by the International Building Code (IBC) as the weight of snow on the ground surface. The ground snow loads for various parts of the United States can be obtained from the contour maps in ASCE 7-16. Some typical values of the ground snow loads from this standard are presented in Table 2.8. Once these loads for the required geographic areas have been established, they must be modified for specific conditions to obtain the snow load for structural design.

According to ASCE 7-16, the design snow loads for flat roofs and sloped roofs can be obtained using the following equations:

where

• р_f = design flat roof snow load.
• р_s = design snow load for a sloped roof.
• р_g = ground snow load.
• I = importance factor. See Table 2.9 for importance factor values, depending on the category of the building.
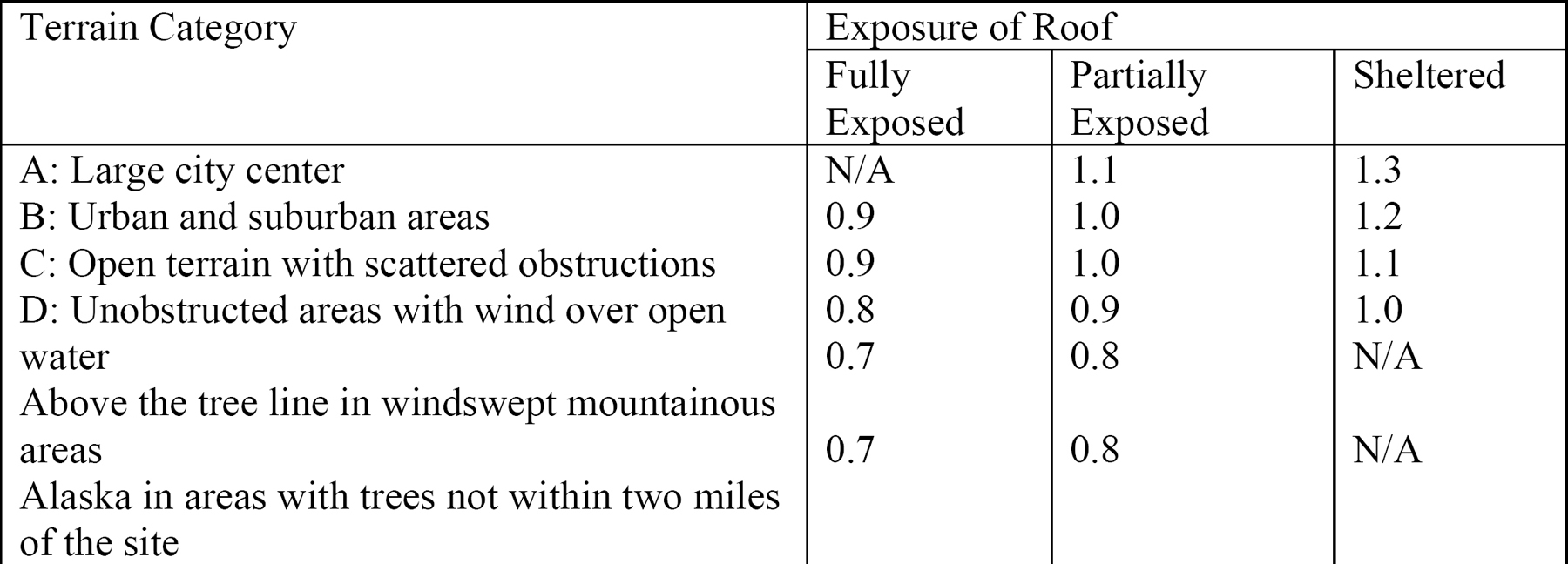
• C_e = exposure factor. See Table 2.10 for exposure factor values, depending on the terrain category.
• C_t = thermal factor. See Table 2.11 for typical values.
• C_s = slope factor. Values of C_s are provided in section 7.4.1 through 7.4.4 of ASCE 7-16, depending on various factors.

Table 2.8. Typical ground snow loads, as specified in ASCE 7-16.

Location	Load (PSF)
Lancaster, PA Yakutat, AK New York City, NY San Francisco, CA Chicago, IL Tallahassee, FL	30 150 30 5 25 0

Table 2.9. Importance factor for snow load, Is, as specified in ASCE 7-16.

Risk Category of Structure	Importance Factor
I II III IV	0.8 1.0 1.1 1.2

Table 2.10. Exposure coefficient, C_e, as specified in ASCE 7-16.

Table 2.11. Thermal factor, C_t, as specified in ASCE 7-16.

Thermal Condition	Thermal Factor
All structures except as indicated below	1.0
Structures kept just above freezing and others with cold, ventilated roofs in which the thermal resistance (R-value) between the ventilated space and the heated space exceeds 25° F × h × ft^2/Btu (4.4 K × m^2/W)	1.1
Unheated and open air structures	1.2
Structures intentionally kept below freezing	1.3
Continuously heated greenhouses with a roof having a thermal resistance (R-value) less than 2.0 ° F × h × ft^2/Btu	0.85

Example 2.4

A single-story heated residential building located in the suburban area of Lancaster, PA is considered partially exposed. The roof of the building slopes at 1 on 20, and it is without overhanging eaves. What is the design snow load on the roof?

Solution

According to Figure 7.2-1 in ASCE 7-16, the ground snow load for Lancaster, PA is

р_g = 30 psf.

Since 30 psf > 20 psf, the rain-on-snow surcharge is not required.

To find the roof slope, use θ = arctan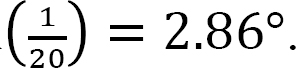

According to ASCE 7-16, since 2.86° < 15°, the roof is considered a low-slope roof. Table 7.3-2 in ASCE 7-16 states that the thermal factor for a heated structure is C_t = 1.0 (see Table 2.11).

According to Table 7.3-1 in ASCE 7-16, the exposure factor for terrain category B, partially exposed is C_e = 1.0 (see Table 2.10).

Table 1.5-2 in ASCE 7-16 states that the importance factor I_s = 1.0 for risk category II (see Table 2.9).

According to equation 2.6, the flat roof snow load is as follows:

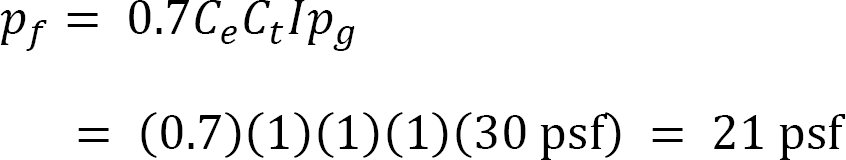
Since 21 psf > 20I_s = (20 psf)(1) = 20 psf. Therefore, the design flat roof snow load is 21 psf.

2.1.4.4 Seismic Loads

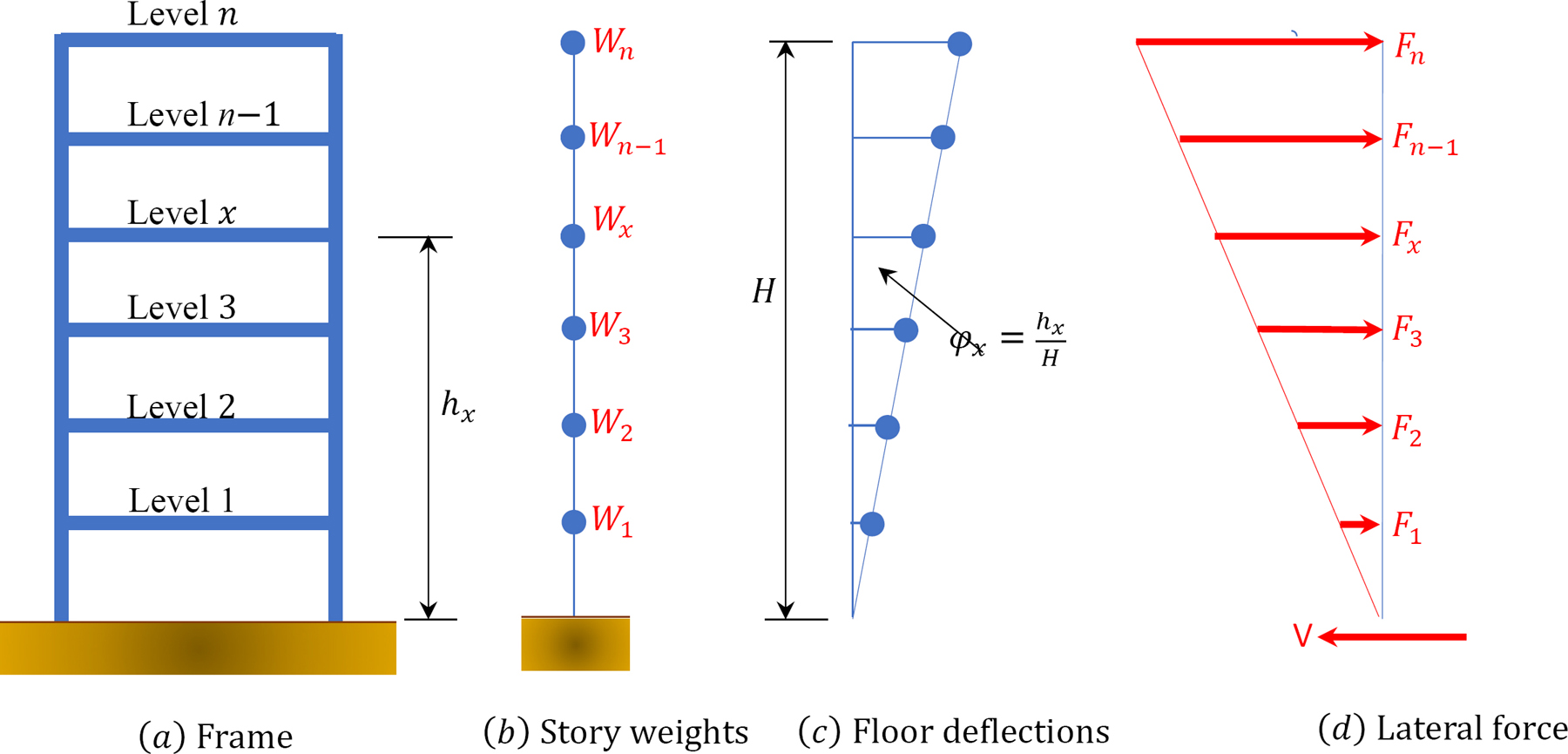
The ground motion caused by seismic forces in many geographic regions of the world can be quite significant and often damages structures. This is particularly notable in regions near active geological faults. Thus, most building codes and standards require that structures be designed for seismic forces in such areas where earthquakes are likely to occur. The ASCE 7-16 standard provides numerous analytical methods for estimating the seismic forces when designing structures. One of these methods of analysis, which will be described in this section, is referred to as the equivalent lateral force (ELF) procedure. The lateral base shear V and the lateral seismic force at any level computed by the ELF are shown in Figure 2.6. According to the procedure, the total static lateral base shear, V, in a specific direction for a building is given by the following expression:

where

V = lateral base shear for the building. The estimated value of V must satisfy the following condition:

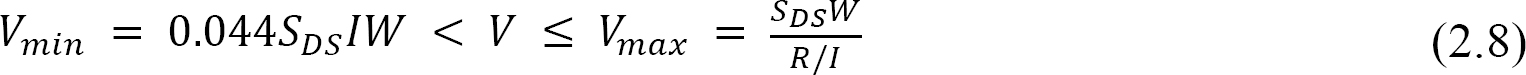
W = effective seismic weight of the building. It includes total dead load of the building and its permanent equipment and partitions.

T = fundamental natural period of a building, which depends on the mass and the stiffness of the structure. It is computed using the following empirical formula:

C_t = building period coefficient. The value of C_t = 0.028 for structural steel moment resisting frames, 0.016 for reinforced concrete rigid frames, and 0.02 for most other structures (see Table 2.12).

ℎ_n = height of the highest level of the building, and x = 0.8 for steel rigid moment frames, 0.9 for reinforced concrete rigid frames, and 0.75 for other systems.

Table 2.12. C_t values for various structural systems.

Structural System	Ct	x
Steel moment resisting frames Eccentrically braced frames (EBF) All other structural systems	0.028 0.03 0.02	0.8 0.75 0.75

S_DI = design spectral acceleration. It is estimated by using a seismic map that provides an earthquake’s intensity of design for structures at locations with T = 1 second.

S_Ds = design spectral acceleration. It is estimated by using a seismic map that provides an earthquake’s intensity of design for structures with T = 0.2 second.

R = response modification coefficient. It accounts for the ability of a structural system to resist seismic forces. The values of R for several common systems are presented in Table 2.13.

I = importance factor. This is a measure of the consequences to human life and damage to property in the event that the structure fails. The value of the importance factor is 1 for office buildings, but equals 1.5 for hospitals, police stations, and other public buildings where loss of more life or damages to property are anticipated should a structure fail.

Table 2.13. Response modification coefficient, R, as specified in ASCE 7-16.

Seismic Force-Resisting System	R
Bearing wall systems Ordinary reinforced concrete shear walls Ordinary reinforced masonry shear walls Light-frame (cold-formed steel) walls sheathed with structural panels rated for shear resistance or steel sheets	4 2
Building frame systems Ordinary reinforced concrete shear walls Ordinary reinforced masonry shear walls Steel buckling-restrained braced frames	5 2 8
Moment-resisting frame systems Steel special moment frames Steel ordinary moment frames Ordinary reinforced concrete moment frames	8 3

Once the total seismic static lateral base shear force in a given direction for a structure has been computed, the next step is to determine the lateral seismic force that will be applied to each floor level using the following equation:

where

F_x = lateral seismic force applied to level x.

W_i and W_x = effective seismic weights at levels i and x.

ℎ_i and ℎ_x = heights from the base of the structure to floors at levels i and x.

= summation of the product W_i and over the entire structure.

k = distribution exponent related to the fundamental natural period of the structure. For T ≤ 0.5s, k = 1.0, and for T ≥ 2.5s, k = 2.0. For T lying between 0.5s and 2.5s, k can be computed using the following relationship:

Fig. 2.6. Equivalent lateral force procedure

Example 2.5

The five-story office steel building shown in Figure 2.7 is laterally braced with steel special moment resisting frames, and it measures 75 ft by 100 ft in the plan. The building is located in New York City. Using the ASCE 7-16 equivalent lateral force procedure, determine the lateral force that will be applied to the fourth floor of the structure. The roof dead load is 32 psf, the floor dead load (including the partition load) is 80 psf, and the flat roof snow load is 40 psf. Ignore the weight of cladding. The design spectral acceleration parameters are S_DS = 0.28, and S_D1 = 0.11.

Fig. 2.7. Five – story office building.

Solution

S_DS = 0.28 and S_D1 = 0.11 (given).

R = 8 for special moment resisting steel frame (see Table 2.13).

An office building is in occupancy risk category II, so I_e = 1.0 (see Table 2.9).

Calculate the approximate fundamental natural period of the building T_a.

C_t = 0.028 and x = 0.8 (from Table 2.12 for steel moment resisting frames).

ℎ_n = Roof height = 52.5 ft

Determine the dead load at each level. Since the flat roof snow load given for the office building is greater than 30 psf, 20% of the snow load must be included in the seismic dead load computations.

The weight assigned to the roof level is as follows:

W_roof = (32 psf)(75 ft)(100 ft) + (20%)(40psf)(75 ft)(100 ft) = 300,000 lb

The weight assigned to all other levels is as follows:

W_i = (80 psf)(75ft)(100 ft) = 600,000 lb

The total dead load is as follows:

W_Total = 300,000 lb + (4)(600,000 lb) = 2700 k

Calculate the seismic response coefficient C_s.

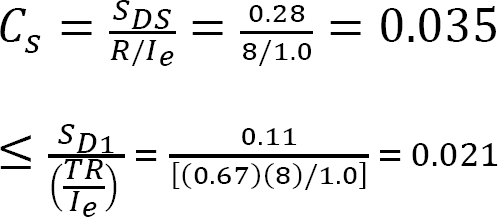
Therefore, C_s = 0.021 > 0.01

Determine the seismic base shear V.

V = C_sW = (0.021)(2700 kips) = 56.7k

Calculate the lateral force applied to the fourth floor.

2.1.4.5 Hydrostatic and Earth Pressures

Retaining structures must be designed against overturning and sliding caused by hydrostatic and earth pressures to ensure the stability of their bases and walls. Examples of retaining walls include gravity walls, cantilever walls, counterfort walls, tanks, bulkheads, sheet piles, and others. The pressures developed by the retained material are always normal to the surfaces of the retaining structure in contact with them, and they vary linearly with height. The intensity of normal pressure, р, and the resultant force, P, on the retaining structure is computed as follows:

Where

γ = unit weight of the retained material.

ℎ = distance from the surface of the retained material and the point under consideration.

2.1.4.6 Miscellaneous Loads

There are numerous other loads that may also be considered when designing structures, depending on specific cases. Their inclusion in the load combinations will be based on a designer’s discretion if they are perceived to have a future significant impact on structural integrity. These loads include thermal forces, centrifugal forces, forces due to differential settlements, ice loads, flooding loads, blasting loads, and more.

2.2 Load Combinations for Structural Design

Structures are designed to satisfy both strength and serviceability requirements. The strength requirement ensures the safety of life and property, while the serviceability requirement guarantees the comfortability of occupancy (people) and the aesthetics of the structure. To meet the afore-stated requirements, structures are designed for the critical or the largest load that would act on them. The critical load for a given structure is found by combining all the various possible loads that a structure may carry during its lifetime. Sections 2.3.1 and 2.4.1 of ASCE 7-16 provide the following load combinations for use when designing structures by the Load and Resistance Factor Design (LRFD) and the Allowable Strength Design (ASD) methods.

For LRFD, the load combinations are as follows:

1.1.4D

2.1.2 D + 1.6L + 0.5(L_rorS or R)

3.1.2D + 1.6(L_r or S or R) + (L or 0.5W)

4.1.2D + 1.0W + L + 0.5(L_r or S or R)

5.0.9D + 1.0W

For ASD, the load combinations are as follows:

1.D

2.D + L

3.D + (L_r or S or R)

4.D + 0.75L + 0.75(L_r or S or R)

5.D + (0.6W)

where

D = dead load.

L = live load due to occupancy.

L_r = roof live load.

S = snow load.

R = nominal load due to initial rainwater or ice, exclusive of the ponding contributions.

W = wind load.

E = earthquake load.

Example 2.6

A floor system consisting of wooden joists spaced 6 ft apart on the center and a tongue and groove wood boarding, as shown in Figure 2.8, supports a dead load (including the weight of the beam and boarding) of 20 psf and a live load of 30 psf. Determine the maximum factored load in lb/ft that each floor joist must support using the LRFD load combinations.

Fig. 2.8. Floor system.

Solution

Dead load D = (6)(20) = 120 lb/ft

Live load L = (6)(30) = 180 lb/ft

Determining the maximum factored loads W_u using the LRFD load combinations and neglecting the terms that have no values, yields the following:

W_u = (1.4)(120) = 168 lb/ft

W_u = (1.2)(120) + (1.6)(180) = 288 lb/ft

W_u = (1.2)(120) + (0.5)(180) = 234 lb/ft

W_u = (1.2)(120) + (0.5)(180) = 234 lb/ft

W_u = (1.2)(120) + (0.5)(180) = 234 lb/ft

W_u = (0.9)(120) = 108 lb/ft

The governing factored load = 288 lb/ft

2.3 Tributary Width and Area

A tributary area is the area of loading that will be sustained by a structural member. For example, consider the exterior beam B1 and the interior beam B2 of the one-way slab system shown in Figure 2.9. The tributary width for B1 is the distance from the centerline of the beam to half the distance to the next or adjacent beam, and the tributary area for the beam is the area bordered by the tributary width and the length of the beam, as shaded in the figure. For the interior beam B2-B3, the tributary width W_T is half the distance to the adjacent beams on both sides.

Fig. 2.9. Tributary area.

2.4 Influence Areas

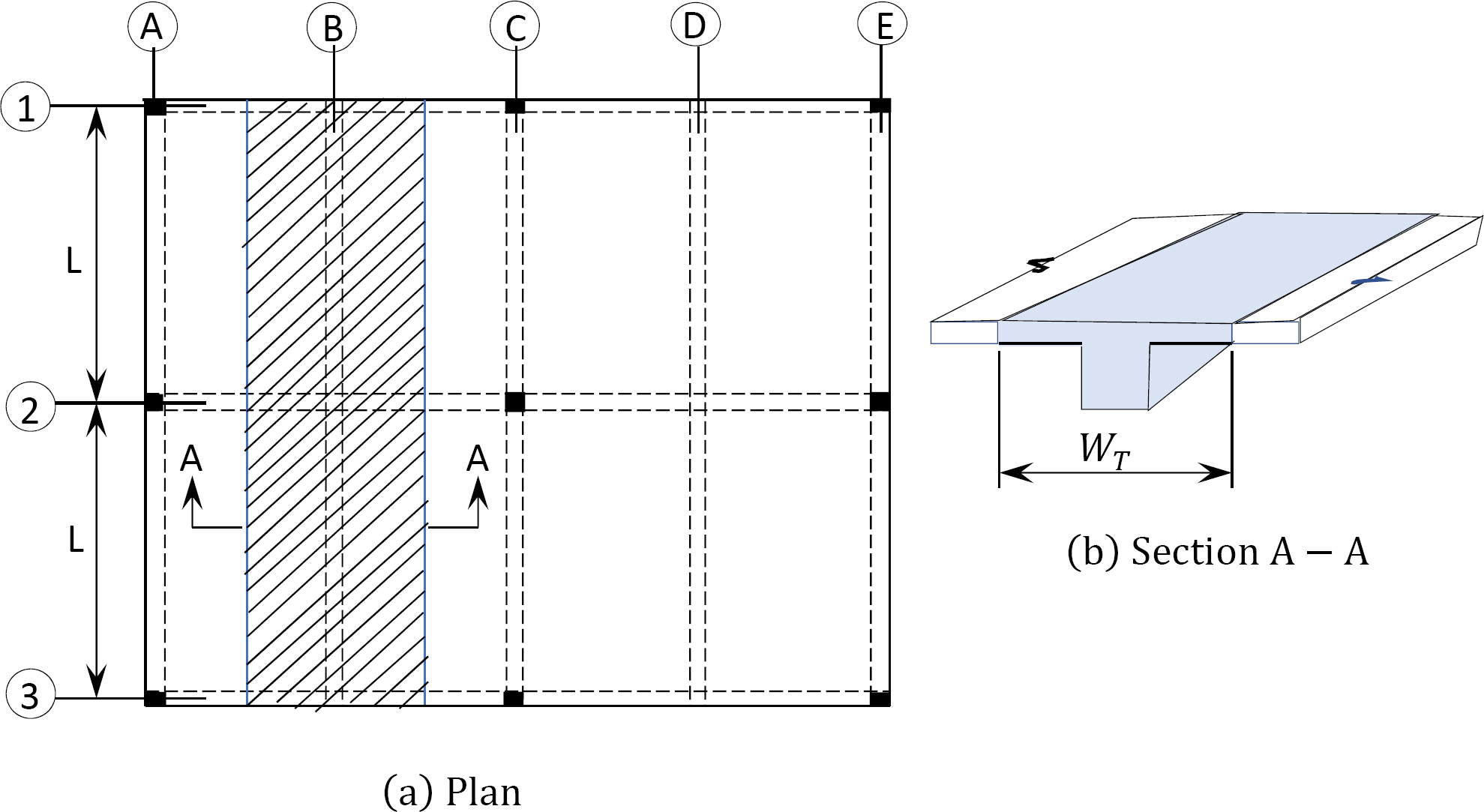
Influence areas are areas of loading that influence the magnitude of loads carried by a particular structural member. Unlike tributary areas, where the load within an area is sustained by the member, all the loads in the influence area are not supported by the member under consideration.

2.5 Live Load Reduction

Most codes and standards allow for reduction in live loads when designing large floor systems, since it is very unlikely that such systems will always support the estimated maximum live loads at every instance. Section 4.7.3 of ASCE 7-16 permits a reduction of live loads for members that have an influence area of A_I ≥ 37.2 m²(400 ft²). The influence area is the product of the tributary area and the live load element factor. The ASCE 7-16 equations for determining the reduced live load based on the influence area are as follows:

where

L = reduced design live load per ft² (or m²).

≥ 0.50 L_o for structural members supporting one floor (e.g. beams, girders, slabs, etc.).

≥ 0.40 L_o for structural members supporting two or more floors (e.g. columns, etc.).

No reduction is permitted for floor live loads greater than 4.79 kN/m²(100 lb/ft²) or for floors of public assembly, such as stadiums, auditoriums, movie theaters, etc., as there is a greater possibility of such floors being overloaded or used as car garages.

L_o = unreduced design live load per ft² (or m²) from Table 2.2 (Table 4.3-1 in ASCE 7-16).

A_T = tributary area of member in ft² (or m²).

K_LL = A_I/A_T = live load element factor from Table 2.14 (see values tabulated in Table 4.7-1 in ASCE 7-16).

A_I = K_LLA_T = influence area.

Table 2.14. Live load element factor.

Building Element	KLL
Interior columns and exterior columns without cantilever slabs	4
Exterior columns with cantilever slabs	3
Corner columns with cantilever slabs	2
Interior beams and edge beams without cantilever slabs	2
All other members, including panels in two-way slabs	1

Example 2.7

A four-story school building used for classrooms has its columns spaced as shown in Figure 2.10. The flat roof loading of the structure is estimated to be 25 lb/ft². Determine the reduced live load supported by an interior column at the ground level.

Fig. 2.10. A four – story schol building.

Solution

Any interior column at the ground level supports the roof load and the live loads on the second, third, and fourth floors.

The tributary area of an interior column is A_T = (30 ft)(30 ft) = 900 ft²

The roof live load is F_R = (25lb/ft²)(900 ft²) = 22,500 lb = 22.5 k

For the floor live loads, use the ASCE 7-16 equations to check for the possibility of a reduction.

L_o = 40 lb/ft² (from Table 4.1 in ASCE 7-16).

If the interior column K_LL = 4, then the influence area A₁ = K_LLA_T = (4)(900 ft²) = 3600 ft².

Since 3600ft² > 400ft², the live load can be reduced using equation 2.14, as follows:

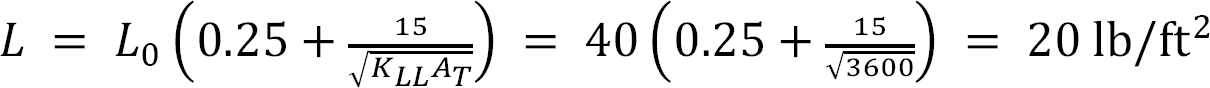
According to Table 4.1 in ASCE 7-16, the reduced load as a fraction of the unreduced floor live load for a classroom is 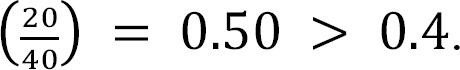Thus, the reduced floor live load is as follows:

F_F = (20 lb/ft²)(900ft²) = 18,000lb = 18 k

The total load supported by the interior column at the ground level is as follows:

F_Total = 22.5 k + 3(18 k) = 76.5 k

Chapter Summary

Structural loads and loading systems: Structural elements are designed for the worst possible load combinations. Some of the loads that could act on a structure are briefly defined below.

Dead loads: These are loads of a constant magnitude in a structure. They include the weight of structure and the loads that are permanently attached to the structure.

Live loads: These are loads of varying magnitudes and positions. They include moveable loads and loads due to occupancy.

Impact loads: Impact loads are sudden or rapid loads applied on a structure over a relatively short period of time compared with other structural loads.

Rain loads: These are loads due to accumulation of water on a roof top after a rainstorm.

Wind loads: These are loads due to wind pressure exerted on structures.

Snow loads: These are loads exerted on a structure by accumulated snow on a rooftop.

Earthquake loads: These are loads exerted on a structure by the ground motion caused by seismic forces.

Hydrostatic and earth pressures: These are loads on retaining structures due to pressures developed by the retained materials. They vary linearly with the height of the walls.

Load combinations: The two building design methods are the Load and Resistance Factor Design method (LRFD) and the Allowable Strength Design method (ASD). Some of the load combinations for these methods are shown below.

LRFD:

1.1.4D

2.1.2 D + 1.6L + 0.5(L_rorS or R)

3.1.2D + 1.6(L_r or S or R) + (L or 0.5W)

4.1.2D + 1.0W + L + 0.5(L_r or S or R)

5.0.9D + 1.0W

ASD:

1.D

2.D + L

3.D + (L_r or S or R)

4.D + 0.75L + 0.75(L_r or S or R)

5.D + (0.6W)

References

ACI (2016), Building Code Requirements for Structural Concrete (ACI 318-14), American Concrete Institute.

ASCE (2016), Minimum Design Loads for Buildings and Other Structures, ASCE 7-16, ASCE.

ICC (2012), International Building Code, International Code Council.

Practice Problems

2.1 Determine the maximum factored moment for a roof beam subjected to the following service load moments:

M_D = 40 psf (dead load moment)

M_Lr = 36 psf (roof live load moment)

M_s = 16 psf (snow load moment)

2.2 Determine the maximum factored load sustained by a column subjected to the following service loads:

P_D = 500 kips (dead load)

P_L = 280 kips (floor live load)

P_S = 200 kips (snow load)

P_E = ±30 kips (earthquake load)

P_w = ±70 kips (wind load)

2.3 The typical layout of a steel-reinforced concrete composite floor system of a library building is shown in Figure P2.1. Determine the dead load in lb/ft acting on a typical interior beam B1-B2 in the second floor. All beams are W12 × 44, spaced at 10 ft o.c. The distributed loads on the second floor are as follows:

2 in. thick sand-cement screed	= 0.25 psf
6 in. thick reinforced concrete slab	= 50 psf
Suspended metal lath and gypsum plaster ceiling	= 10 psf
Electrical and mechanical services	= 4 psf

Typical floor plan

Fig. P2.1. A steel – reinforced concrete composite floor system.

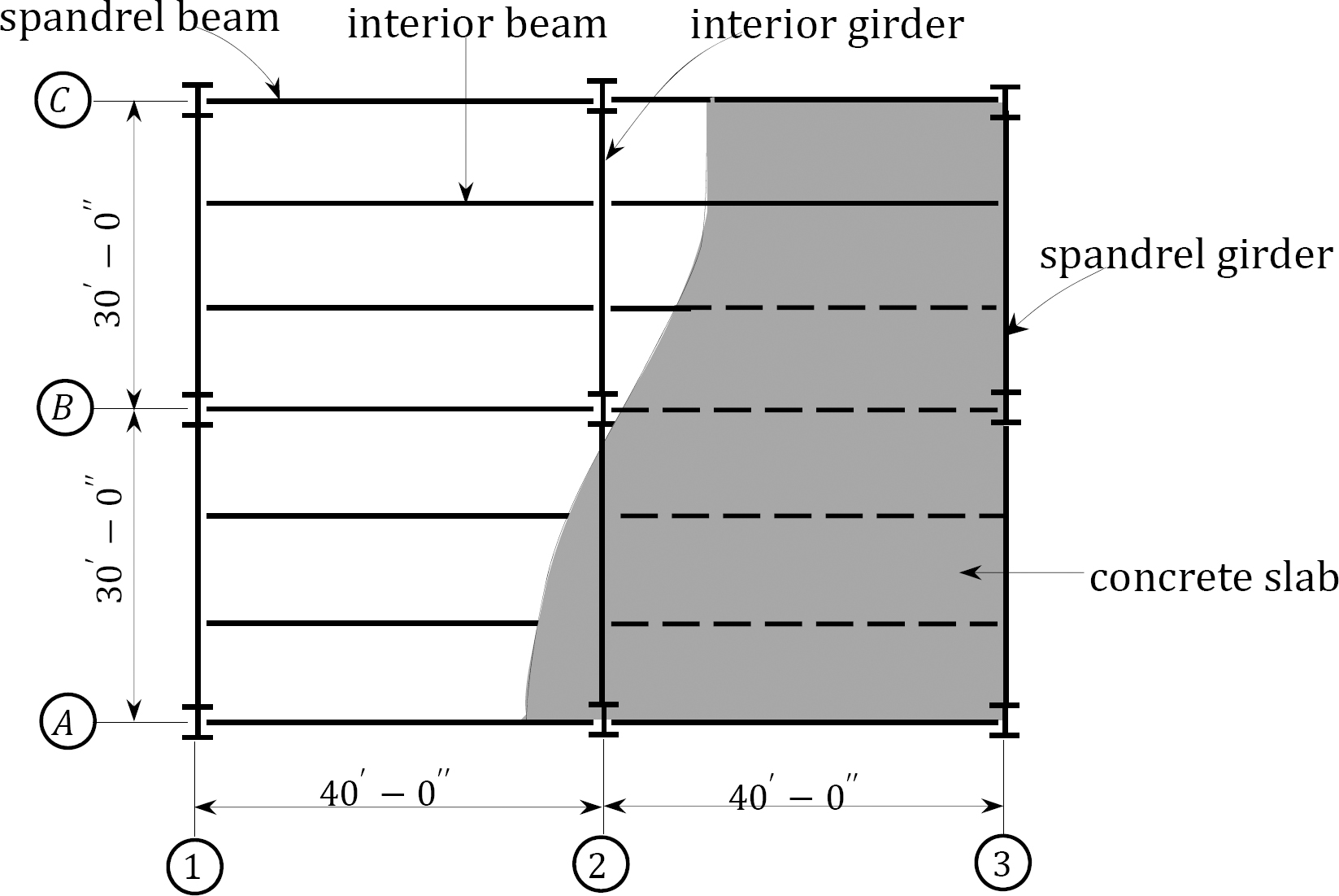
2.4 The second-floor layout of an elementary school building is shown in Figure P2.1. The floor finishing is similar to that of practice problem 2.3, with the exception that the ceiling is an acoustical fiberboard of a minimum design load of 1 psf. All beams are W12 × 75, with a weight of 75 lb/ft, and all girders are W16 × 44, with a self-weight of 44 lb/ft. Determine the dead load on a typical interior girder A2-B2.

2.5 The second-floor layout of an office facility is shown in Figure P2.1. The floor finishing is similar to that of practice problem 2.3. Determine the total dead load applied to the interior column B2 at the second floor. All beams are W14 × 75, and all girders are W18 × 44.

2.6 A four-story flat roof hospital building shown in Figure P2.2 has concentrically braced frames as its lateral force resisting system. The weight at each floor level is indicated in the figure. Determine the seismic base shear in kips given the following design data:

S₁ = 1.5g

S_s = 0.6g

Site class = D

Fig. P2.2. A four – story flat roof building.

2.7 Use ASCE 7-16 to determine the snow load (psf) for the building shown in Figure P2.3. The following data apply to the building:

Ground snow load = 30 psf

Roof is fully exposed with asphalt shingles.

Roof’s slope angle = 25°

Open terrain

Occupancy Category I

Unheated structure

Fig. P2.3. A sample roof.

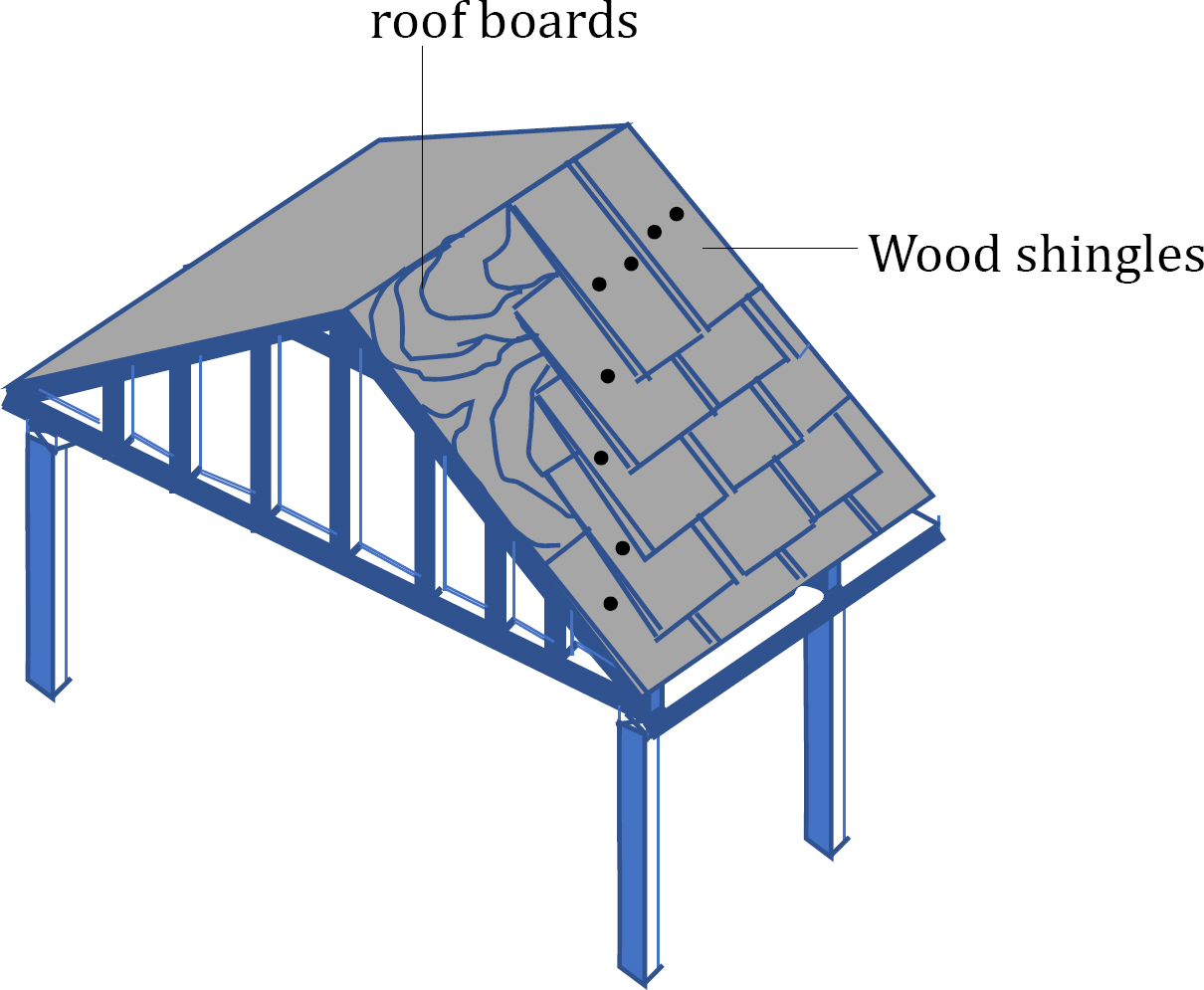
2.8. In addition to the design snow load computed in practice problem 2.7, the roof of the building in Figure P2.3 is subjected to a dead load of 16 psf (including the weight of a truss, roof board, and asphalt shingle) on the horizontal plane. Determine the uniform load acting on the interior truss, if the trusses are 6ft-0in on center.

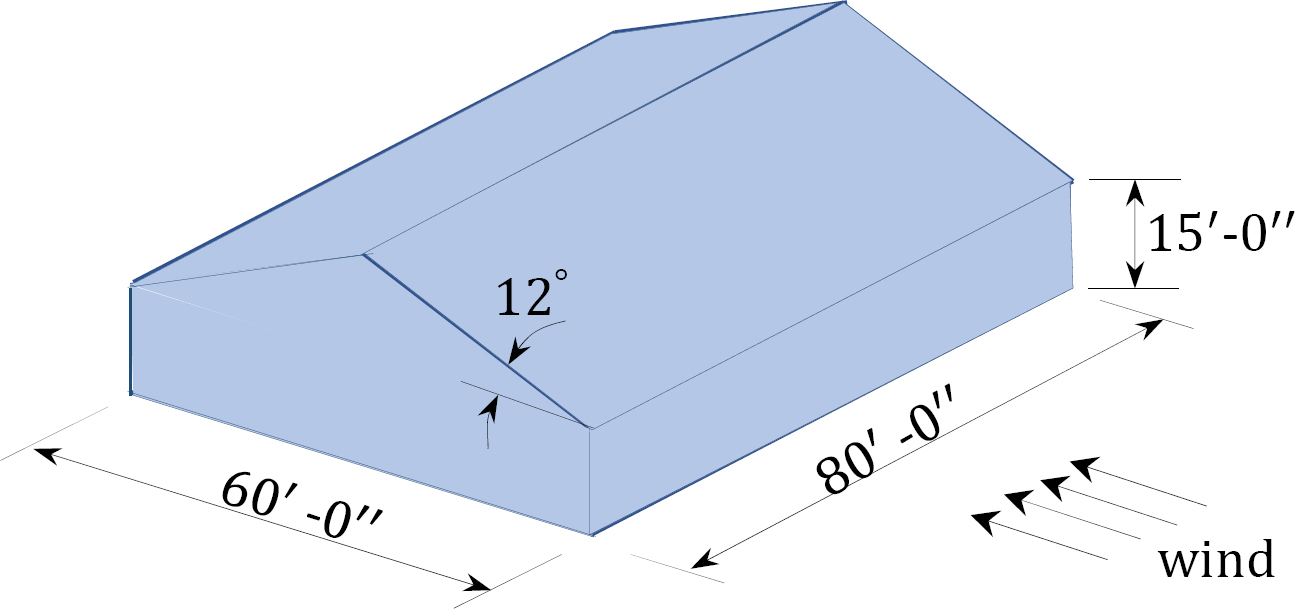
2.9 Wind blows at a speed of 90 mph on the enclosed storage facility shown in Figure P2.4. The facility is situated on a flat terrain with an exposure category B. Determine the wind velocity pressure in psf at the eave height of the facility. The topographic factor is K_zt = 1.0.

Fig. P2.4. An enclosed storgae facility.