1.10: Force Method of Analysis of Indeterminate Structures
- Page ID
- 17617
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The force method of analysis, also known as the method of consistent deformation, uses equilibrium equations and compatibility conditions to determine the unknowns in statically indeterminate structures. In this method, the unknowns are the redundant forces. A redundant force can be an external support reaction force or an internal member force, which if removed from the structure, will not cause any instability. This method entails formulating a set of compatibility equations, depending on the number of the redundant forces in the structure, and solving these equations simultaneously to determine the magnitude of the redundant forces. Once the redundant forces are known, the structure becomes determinate and can be analyzed completely using the conditions of equilibrium.
For an illustration of the method of consistent deformation, consider the propped cantilever beam shown in Figure 10.1a. The beam has four unknown reactions, thus is indeterminate to the first degree. This means that there is one reaction force that can be removed without jeopardizing the stability of the structure. The structure that remains after the removal of the redundant reaction is called the primary structure. A primary structure must always meet the equilibrium requirement. A careful observation of the structure being considered will show that there are two possible redundant reactions and two possible primary structures (see Fig. 10b and Fig. 10d). Taking the vertical reaction at support B and the reactive moments at support A as the redundant reactions, the primary structures that remain are in a state of equilibrium. After choosing the redundant forces and establishing the primary structures, the next step is to formulate the compatibility equations for each case by superposition of some sets of partial solutions that satisfy equilibrium requirements. Equations 10.1 and 10.2 satisfy options 1 and 2, respectively. The terms ∆BP, θAP, δBB, and αAA are referred to as flexibility or compatibility coefficients or constants. The first subscript in a coefficient indicates the position of the displacement, and the second indicates the cause and the direction of the displacement. For example, ∆BP implies displacement at point B caused by the load P in the direction of the load P. The compatibility coefficients can be computed using the Maxwell-Betti Law of Reciprocal, which will be discussed in the subsequent section.



where
M = moment in the primary structure due to the applied load P.
m = moment in the primary structure due to a unit load applied at B.
mθ = moment in the primary structure due to a unit moment applied at A.
Procedure for Analysis of Indeterminate Structures by the Method of Consistent Deformation
- Determine the degree of indeterminacy of the structure.
- Choose the redundant reactions from the indeterminate structure.
- Remove the chosen redundant reactions to obtain the primary structure.
- Formulate the compatibility equations. The number of the equations must match the number of redundant forces.
- Compute the flexibility coefficients.
- Substitute the flexibility coefficients into the compatibility equations.
- In the case of several redundant reactions, solve the compatibility equations simultaneously to determine the redundant forces or moments.
- Apply the computed redundant forces or moments to the primary structure and evaluate other functions, such as bending moment, shearing force, and deflection, if desired, using equilibrium conditions.
10.2 Maxwell-Betti Law of Reciprocal Deflections
The Maxwell-Betti law of reciprocal deflections establishes the fact that the displacements at two points in an elastic structure subjected to a unit load successively at those points are the same in magnitude. This law helps reduce the computational efforts required to obtain the flexibility coefficients for the compatibility equations when analyzing indeterminate structures with several redundant restraints by force method. The Maxwell-Betti law of reciprocal deflection states that the linear displacement at point A due to a unit load applied at B is equal in magnitude to the linear displacement at point B due to a unit load applied at A for a stable elastic structure.
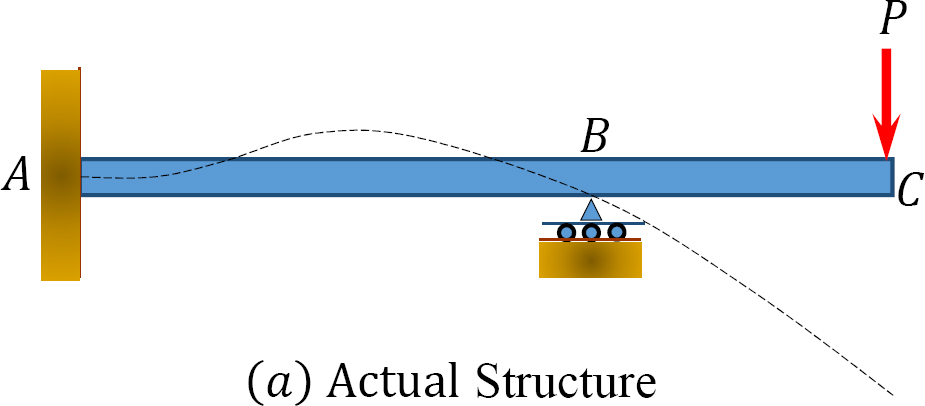
To prove the Maxwell-Betti law of reciprocal deflections, consider a beam subjected to the loads P1 and P2 at point 1 and point 2, successively, as shown in Figure 10.2a and Figure 10.2b.
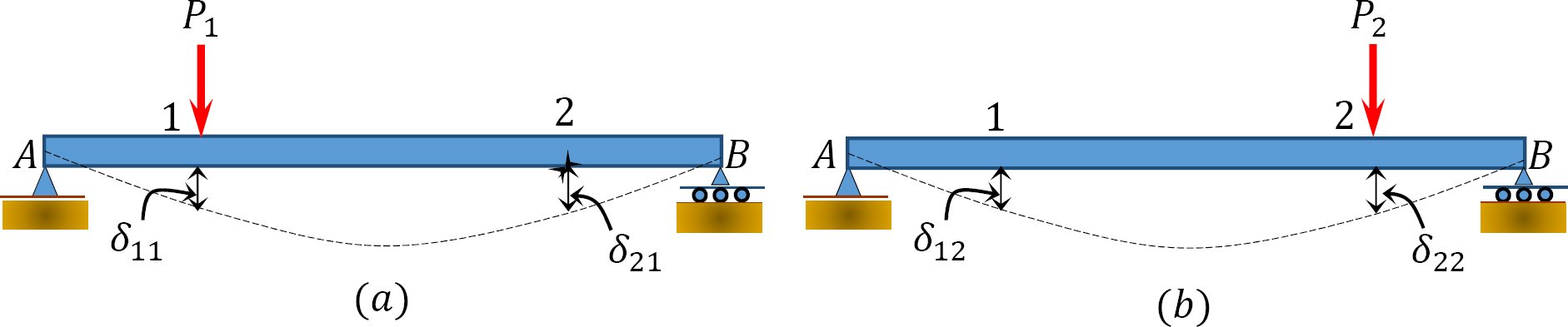
Case 1:
Apply P1, followed by P2.
Work done at point 1 when P1 is applied:

where
δ11 = the deflection at point 1 due to the gradually applied load P1.
Work done at points 1 and 2 when P2 is applied and P1 is still in place:

where
δ12 and δ22 = the deflections at point 1 and point 2, respectively, when the load P2 is gradually at point 2.
Total work done WT:

Case 2:
Apply P2, followed by P1.
Work done at point 1 when P1 is applied:

Work done at points 1 and 2 when P1 is applied and P2 is still in place:

Total work done WT:

Equate the total of both cases (from equations 3 and 6).
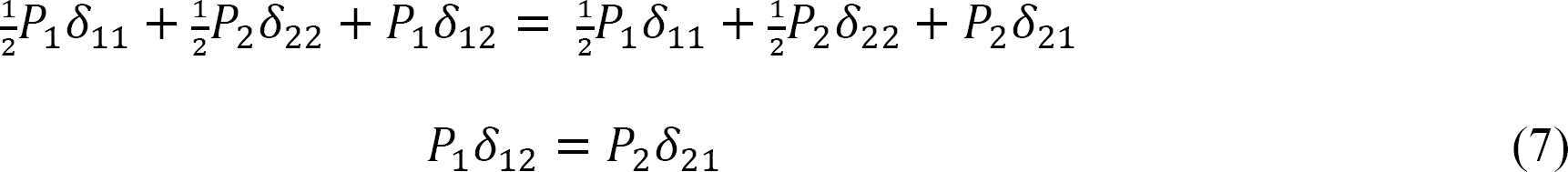
Substituting P1 = P2 = 1 into equation 7 suggests the following:

The Maxwell-Betti law is also applicable for reciprocal rotation. The theorem for reciprocal rotation states that the rotation at point B due to a unit couple moment applied at point A is equal in magnitude to the rotation at A due to a unit couple moment applied at point B. This is expressed as follows:

where
αAB = the rotation at a point A due to a unit couple moment applied at B.
αBA = the rotation at a point B due to a unit couple moment applied at A.
10.3 Analysis of Indeterminate Beams and Frames
The analyses of indeterminate beams and frames follow the general procedure described previously. First, the primary structures and the redundant unknowns are selected, then the compatibility equations are formulated, depending on the number of the unknowns, and solved. There are several methods of computation of flexibility coefficients when analyzing indeterminate beams and frames. These methods include the use of the Mohr integral, deflection tables, and the graph multiplication method. These methods are illustrated in the solved example problems in this section.
10.3.1 Computation of Flexibility Coefficients Using the Mohr Integral
The Mohr integral for obtaining the flexibility coefficient for beams and frames is expressed as follows:

where
- M = moment in the primary structure due to the applied load P.
- m = moment in the primary structure due to a unit load applied at B.
- mθ = moment in the primary structure due to a unit moment applied at A.
Example 10.1
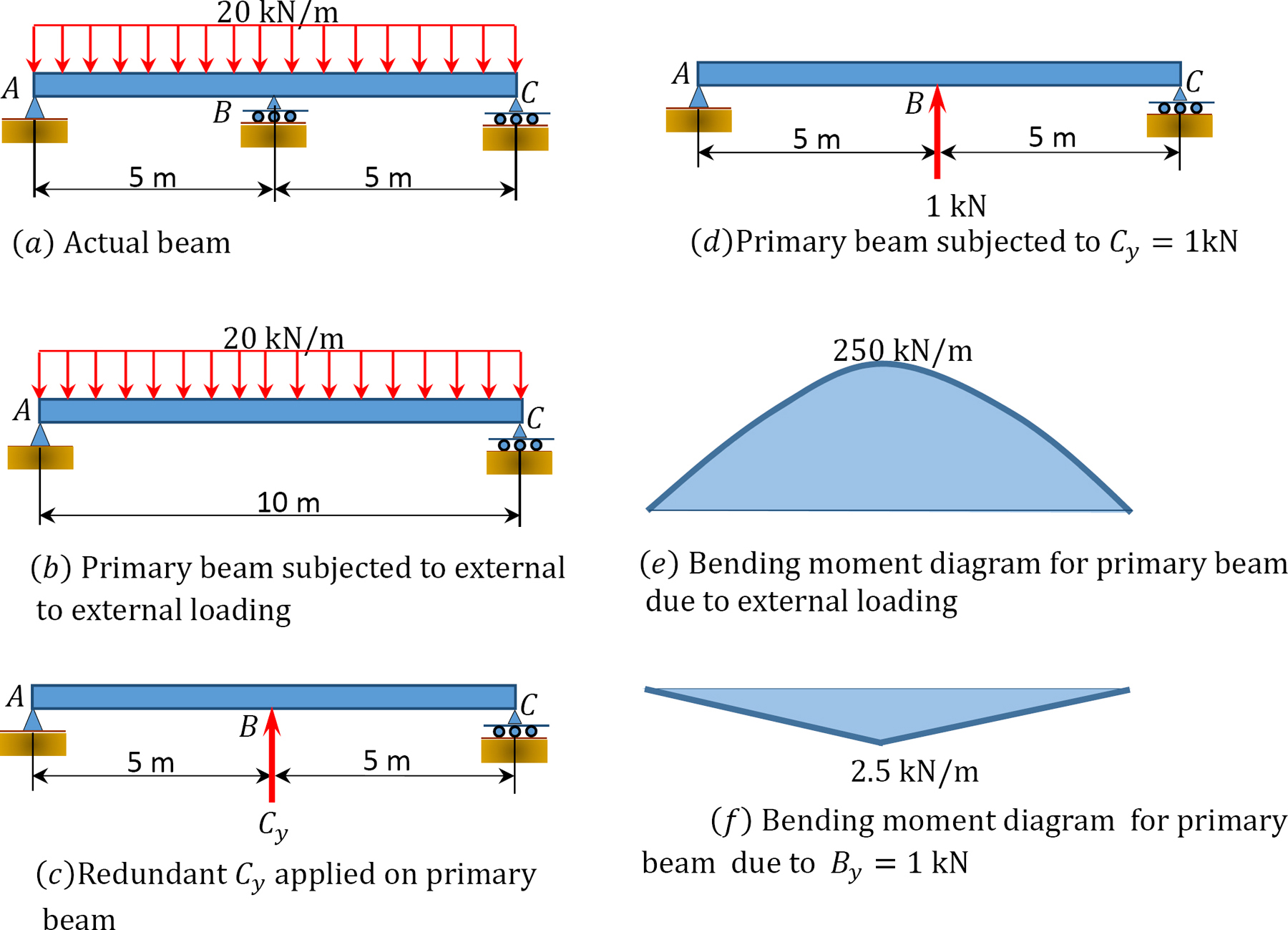
Determine the reactions in the beam shown in Figure 10.3a. Use the method of consistent deformation to carry out the analysis. All flexibility coefficients are determined by integration. EI = constant.
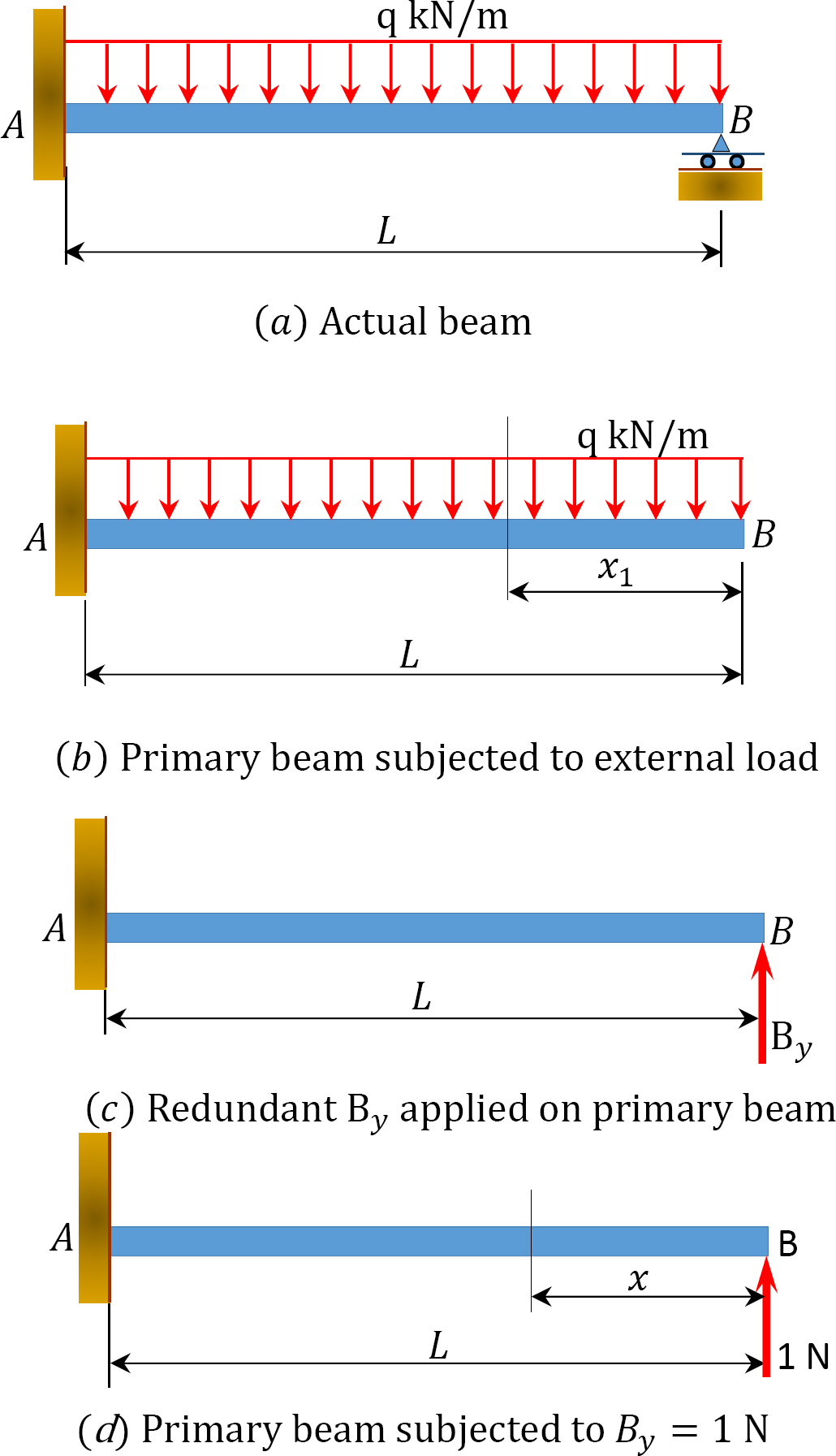
Solution
Classification of structure. There are four unknown reactions in the beam: three unknown reactions at the fixed end A and one unknown reaction at the prop B. Since there are three equations of equilibrium on a plane, it implies that the beam has one unknown reaction in excess of the equations of equilibrium on a plane, thus it is indeterminate to one degree.
Choice of primary structure. There may be more than one possible choice of primary structure. For the given propped cantilever beam, the prop at B will be selected as the redundant. Thus, the primary structure is as shown in Figure 10.3b.
Compatibility equation. The number of compatibility equations will always match the number of the redundant reactions in a given structure. For the given cantilever beam, the number of compatibility equations is one and is written as follows:
∆BP + ByδBB = 0
The flexibility or compatibility coefficients ∆BP and δBB can be computed by several methods, including the integration method, the graph multiplication method, and the table methods. For this example, the flexibility coefficients are computed using the integration method.
The bending moment expressions for the primary beam subjected to external loading is written as follows:
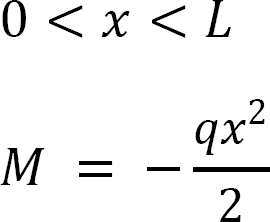
The bending moment in the primary beam subjected to By = 1 kN is as follows:

Using integration to obtain the flexibility coefficients suggests the following:

Putting the computed flexibility coefficients into the compatibility equation suggests the following:
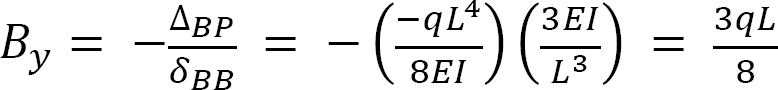
Example 10.2
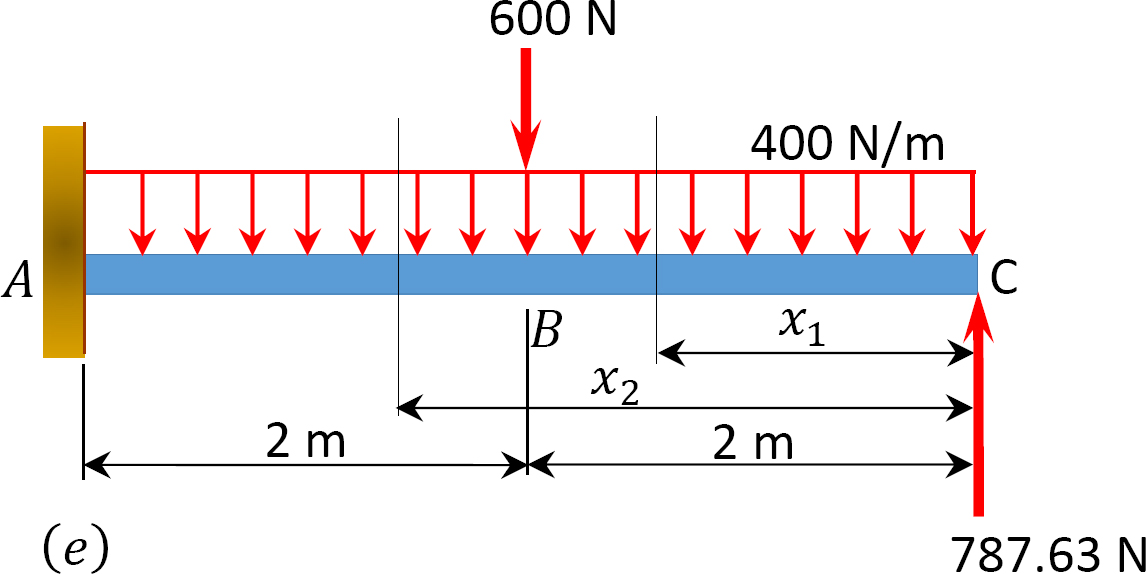
Determine the support reactions and draw the bending moment and the shearing force diagrams for the indeterminate beam shown in Figure 10.4. Use the method of consistent deformation. EI = constant.
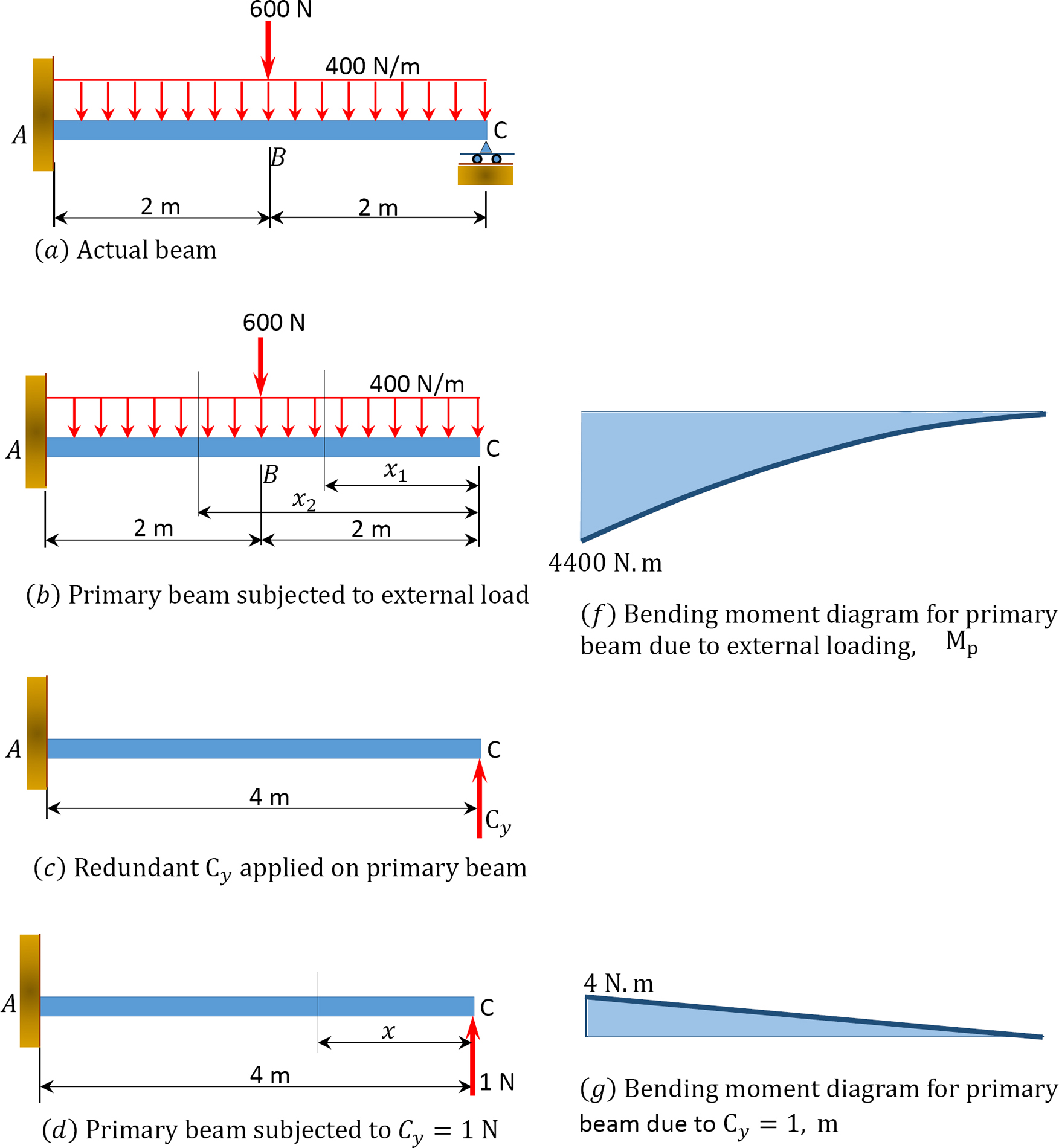
Solution
Classification of structure. There are four unknown reactions in the beam: three unknown reactions at the fixed end A and one unknown reaction at the prop C. Since there are three equations of equilibrium on a plane, it implies that the beam has one unknown reaction in excess of the equations of equilibrium on a plane. Thus, it is indeterminate to one degree.
Choice of primary structure. There may be more than one possible choice of primary structure. For the given propped cantilever beam, the reaction at C is selected as the redundant reaction. Thus, the primary structure is as shown in Figure 10.4b.
Compatibility equation. The number of compatibility equations will always match the number of the redundant reactions in a given structure. For the given cantilever beam, the number of compatibility equations is one and is written as follows:
∆CP + CyδCC = 0
The flexibility or compatibility coefficients ∆CP and δCC are computed using the integration method.
The bending moment expressions for segments AB and BC of the primary beam subjected to an external loading is written as follows:
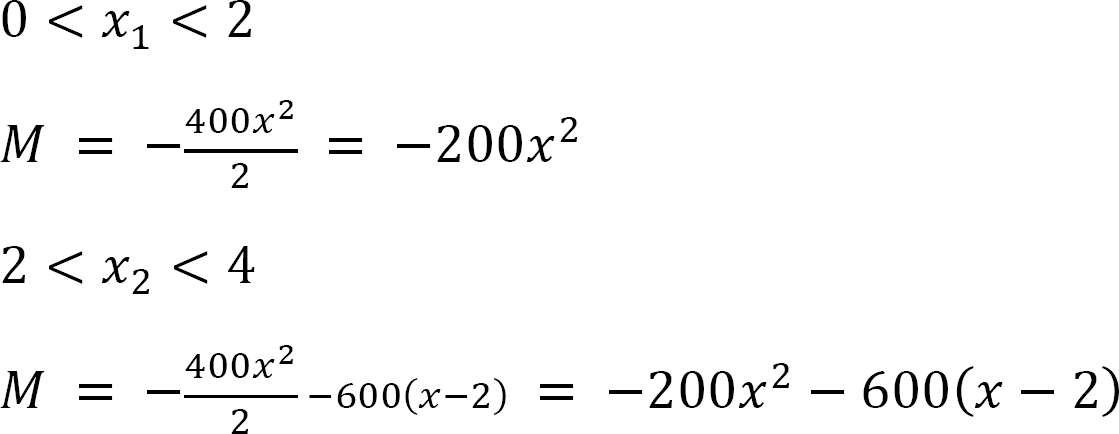
The bending moment in the primary beam subjected to Cy = 1N is written as follows:
M = x
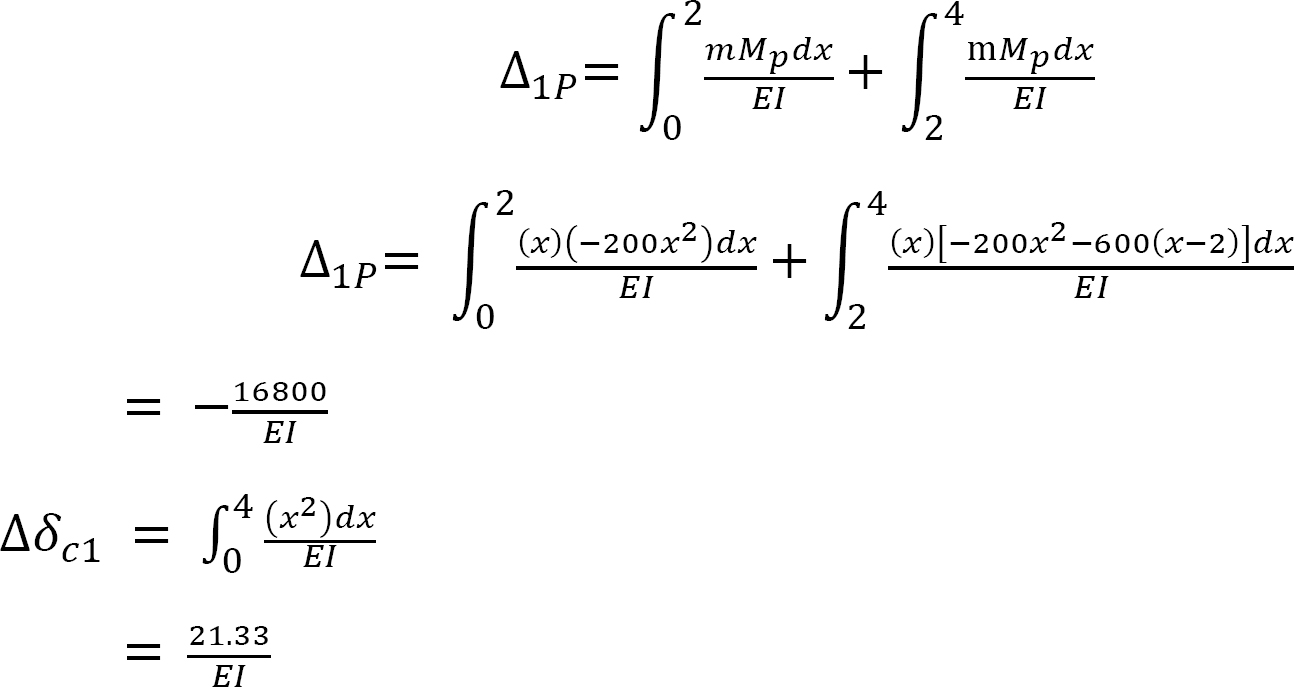
Putting the computed flexibility coefficients into the compatibility equation suggests the following:

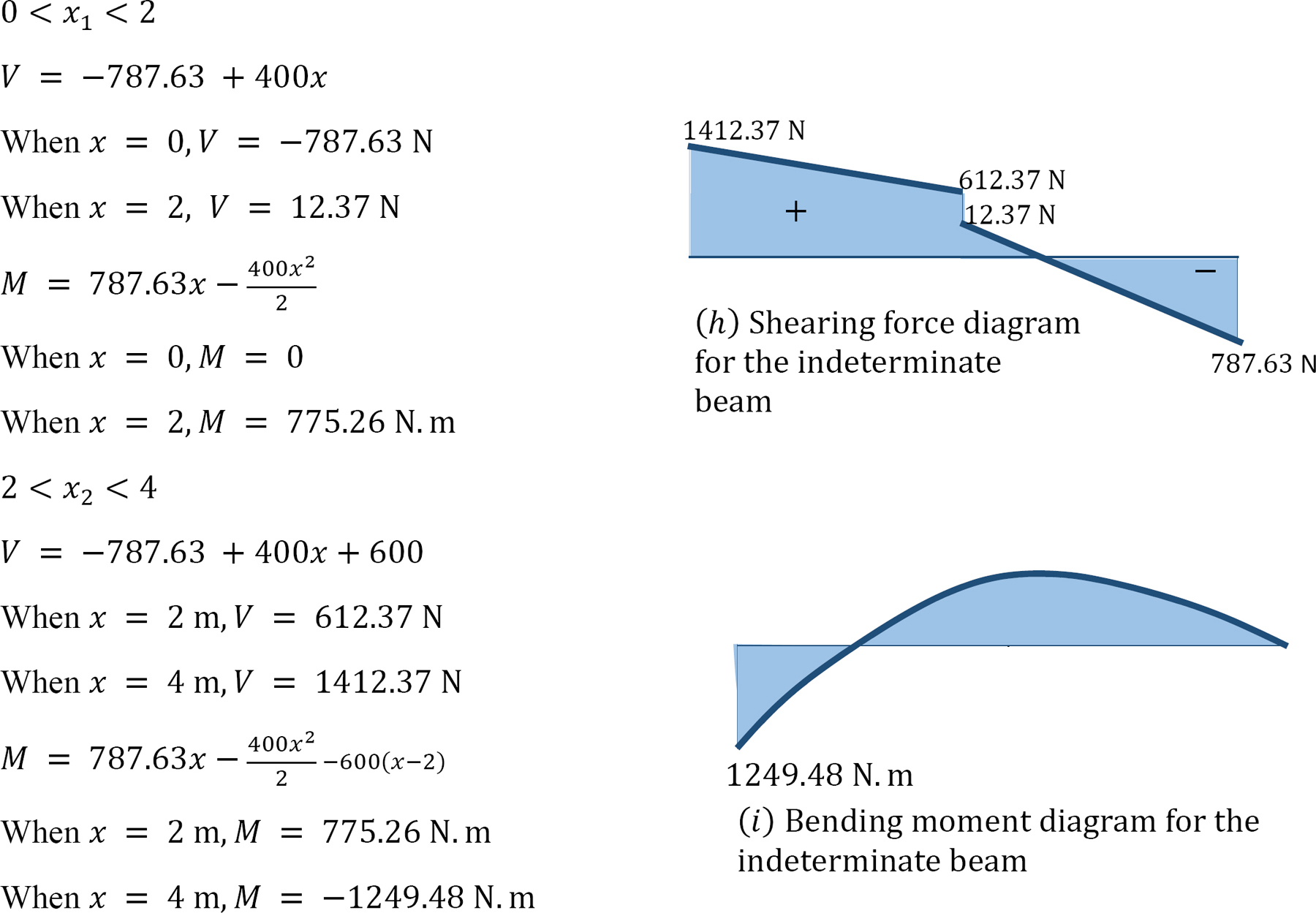
10.3.2 Computation of Flexibility Coefficients by Graph Multiplication Method
The computation of the flexibility coefficients for the compatibility equations by the method of integration can be very lengthy and cumbersome, especially for indeterminate structures with several unknown redundant forces. In such instances, obtaining the coefficients by the graph multiplication method is time-saving. The graph multiplication method is based on the premise that the integral 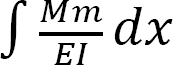 contains the product of two moment graphs M and m. To derive the formula for the graph multiplication method, consider the two moment diagrams M′ and M, as shown in Figure 10.5. The graph of M′ is linear, while that of M is of an arbitrary function.
contains the product of two moment graphs M and m. To derive the formula for the graph multiplication method, consider the two moment diagrams M′ and M, as shown in Figure 10.5. The graph of M′ is linear, while that of M is of an arbitrary function.
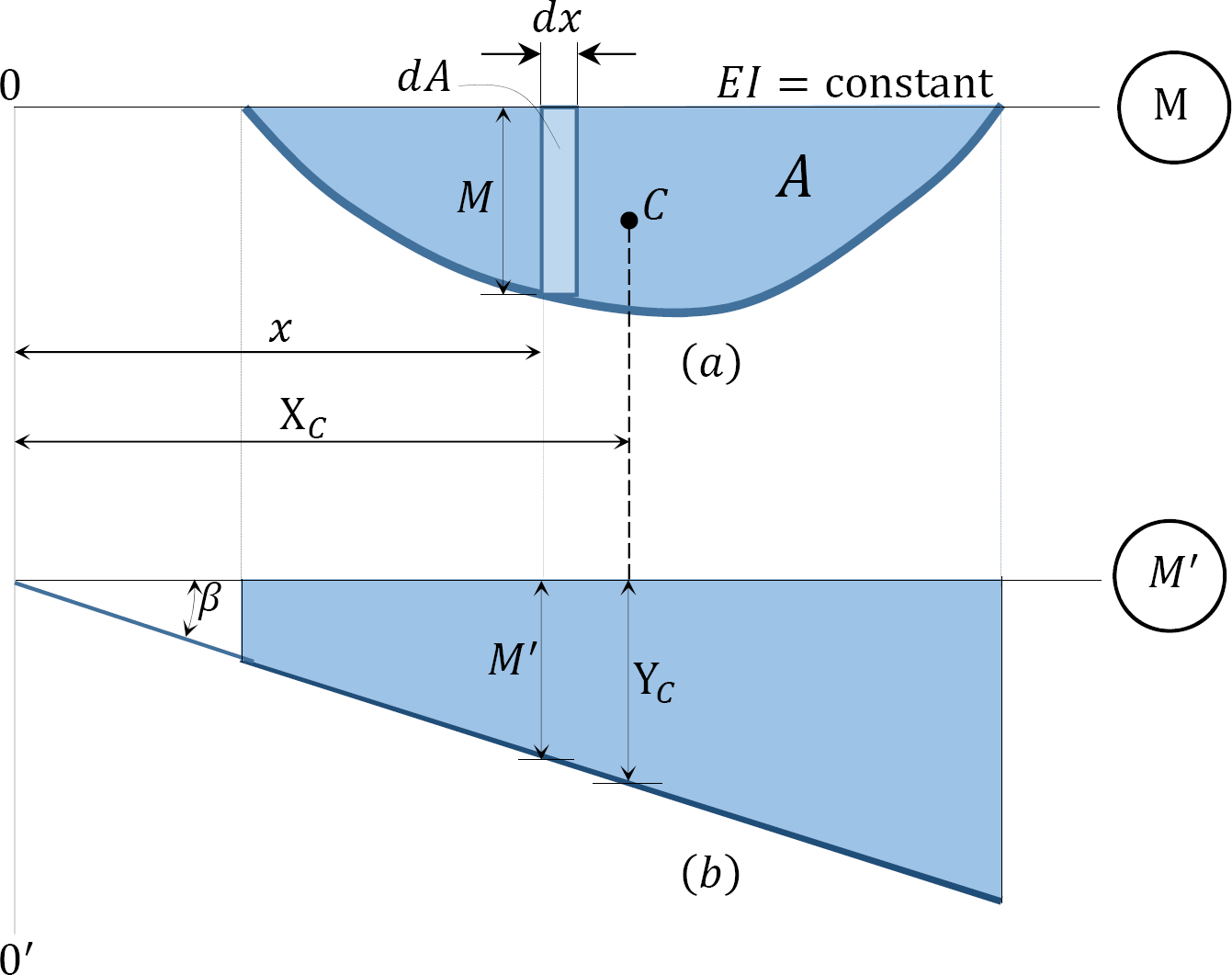
Assuming the flexural rigidity EI is constant, the integral of the product of these two moment diagrams can be expressed as follows:



Substituting equation 2 and 3 into equation 1 suggests the following:
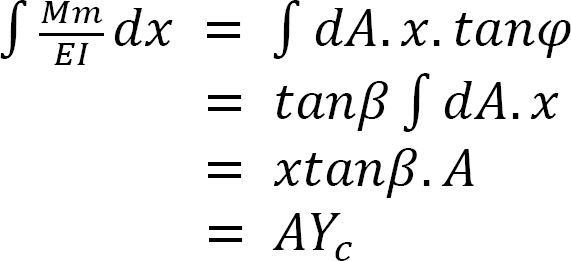

As suggested by equation 10.6, the integral of the product of two moment diagrams is equal to the product of the area of one of the moment diagrams (preferably the diagram with the arbitrary outline) and the ordinate in the second moment diagram with a straight outline, lying on a vertical line passing through the centroid of the first moment diagram.
Example 10.3
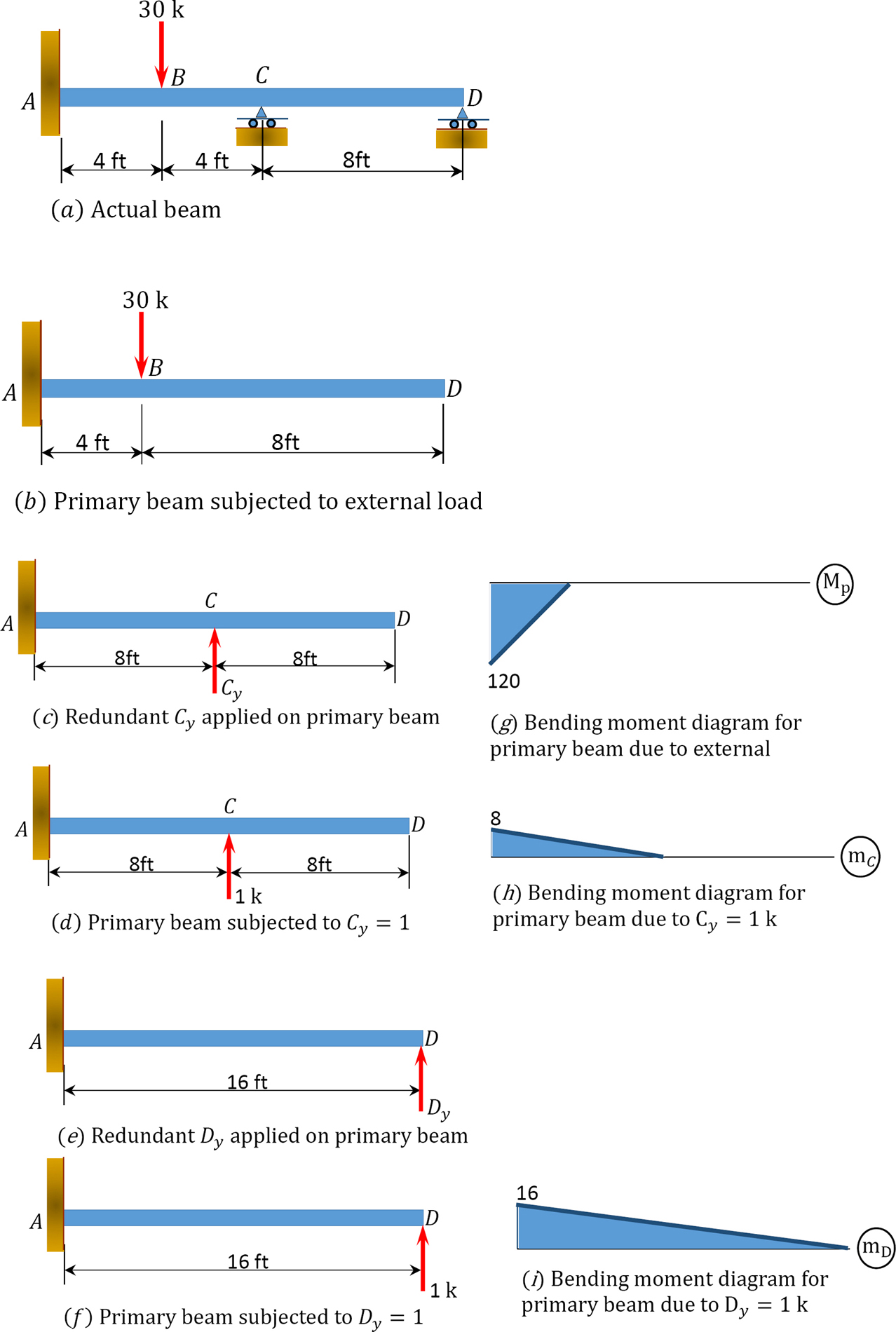
Determine the reactions at supports A, C, and D of the beam shown in Figure 10.6a. A is a fixed support, while C and D are roller supports. EI = constant.
Solution
Classification of structure. There are five unknown reactions in the beam. Thus, the degree of indeterminacy of the structure is two.
Choice of primary structure. The supports at C and D are chosen as the redundant reactions. Therefore, the primary structure is a cantilever beam subjected to the given concentrated load shown in Figure 10.6b. The primary structure subjected to the redundant unknowns are shown in Figure 10.6c, Figure 10.6d, Figure 10.6e, and Figure 10.6f.
Compatibility equation. There are two compatibility equations, as there are two redundant unknown reactions. The equations are as follows:
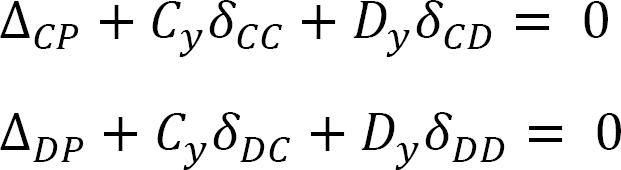
The first alphabets of the subscript of the flexibility coefficients indicate the location of the deflection, while the second alphabets indicate the force causing the deflection. Using the graph multiplication method, the coefficients are computed as follows:
Using the graph multiplication method, the flexibility coefficients are computed as follows:
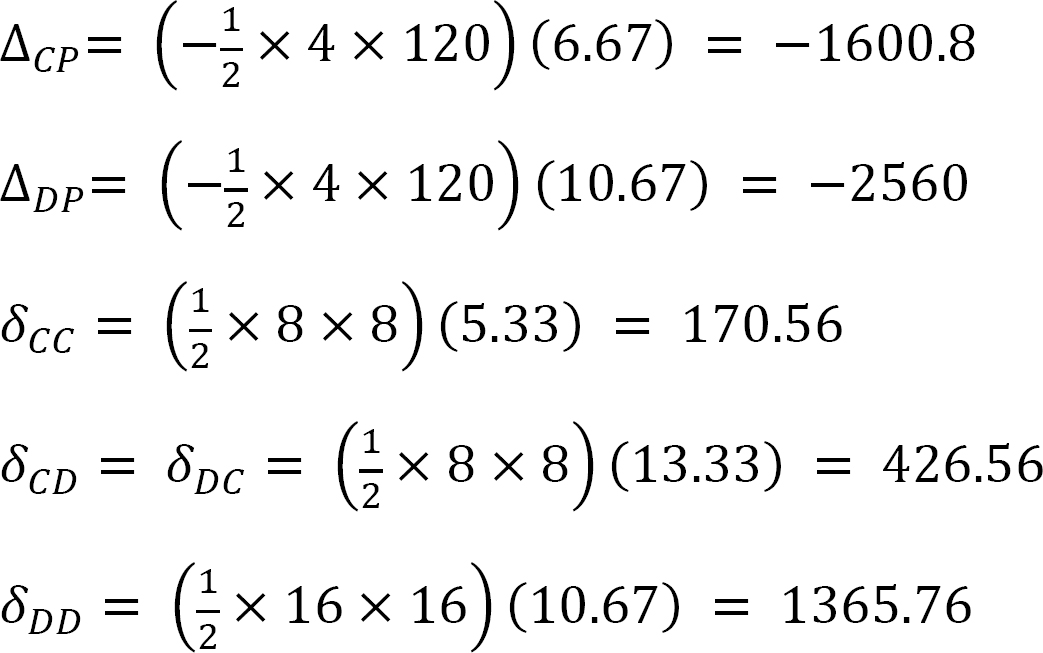
Substituting the flexibility coefficients into the compatibility equation suggests the following two equations, with two unknowns:
–1600.8 + 170.56Cy + 426.56Dy = 0
–2560 + 426.56Cy + 1365.76Dy = 0
Solving both equations simultaneously suggests the following:
Cy = 21.46 k
Dy = –4.83 k
The determination of the reactions at support A is as follows:
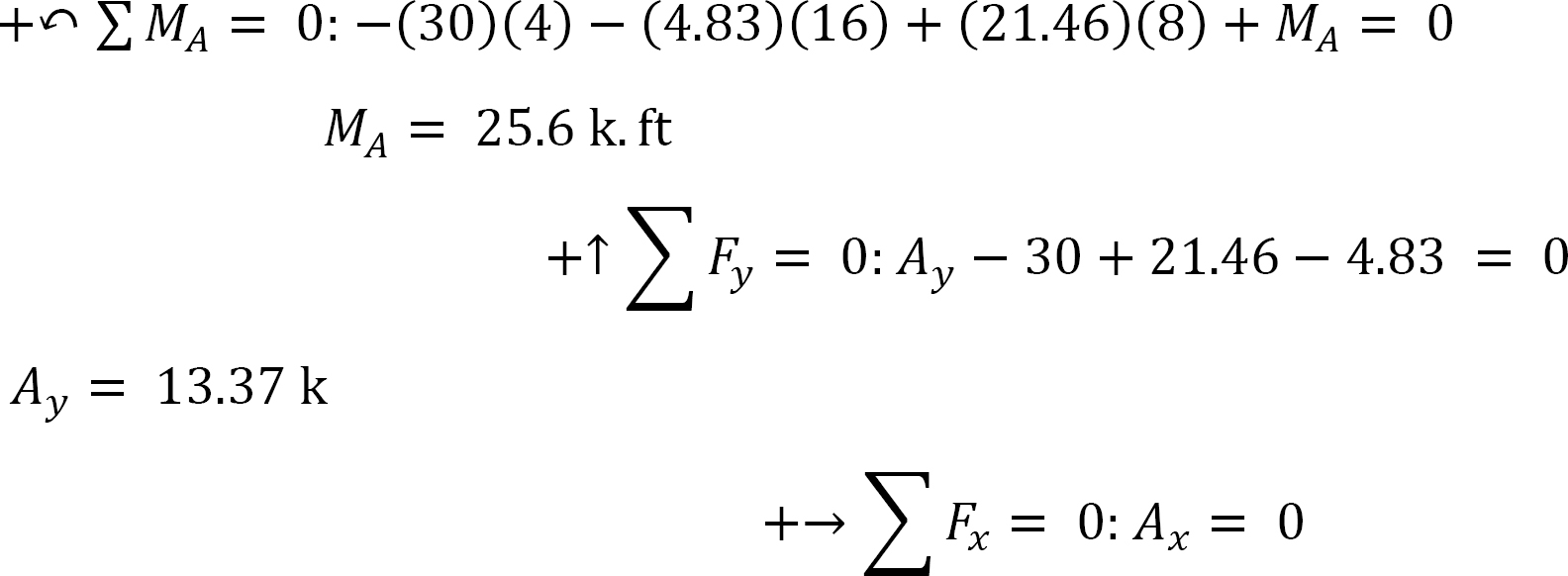
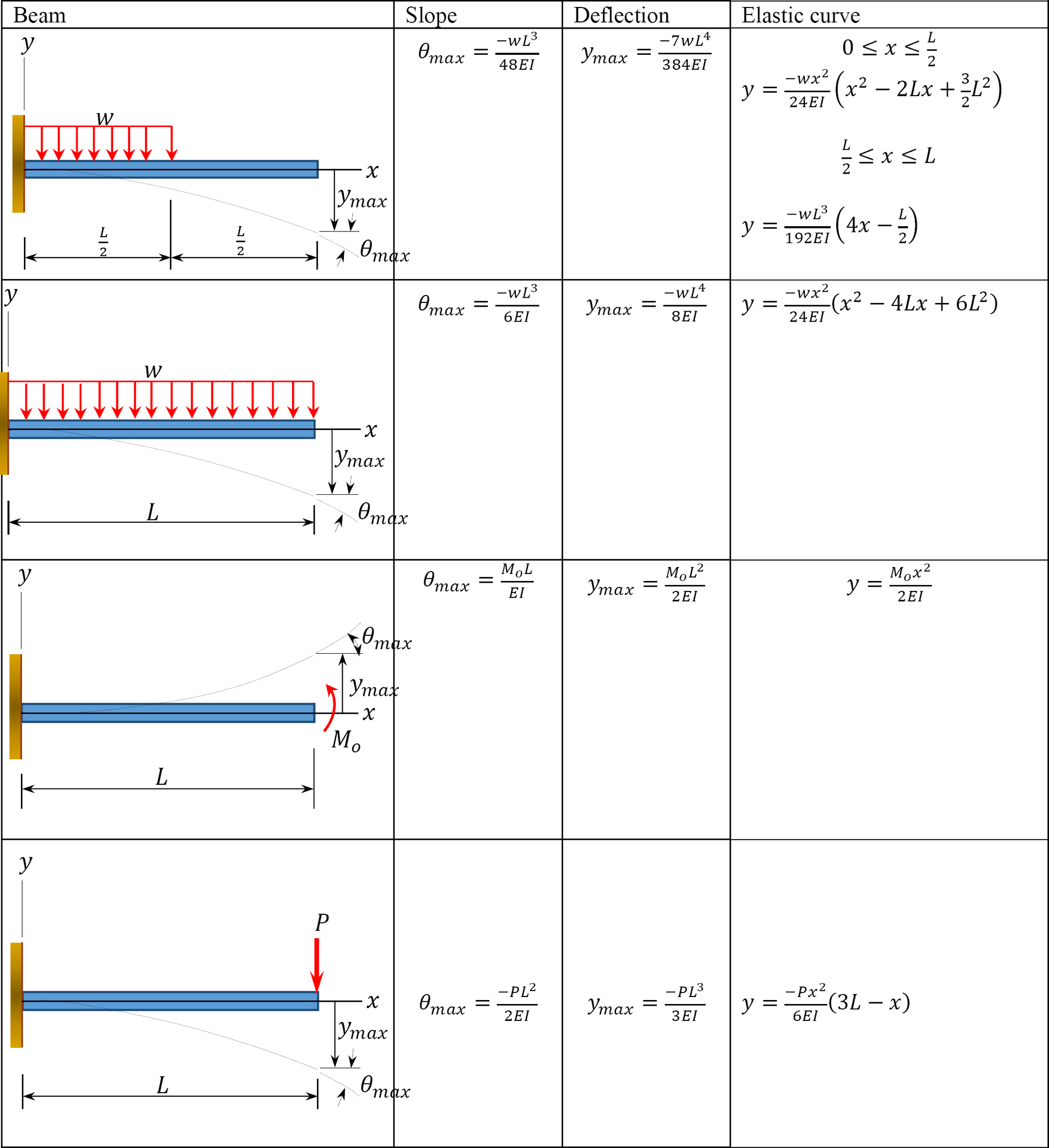
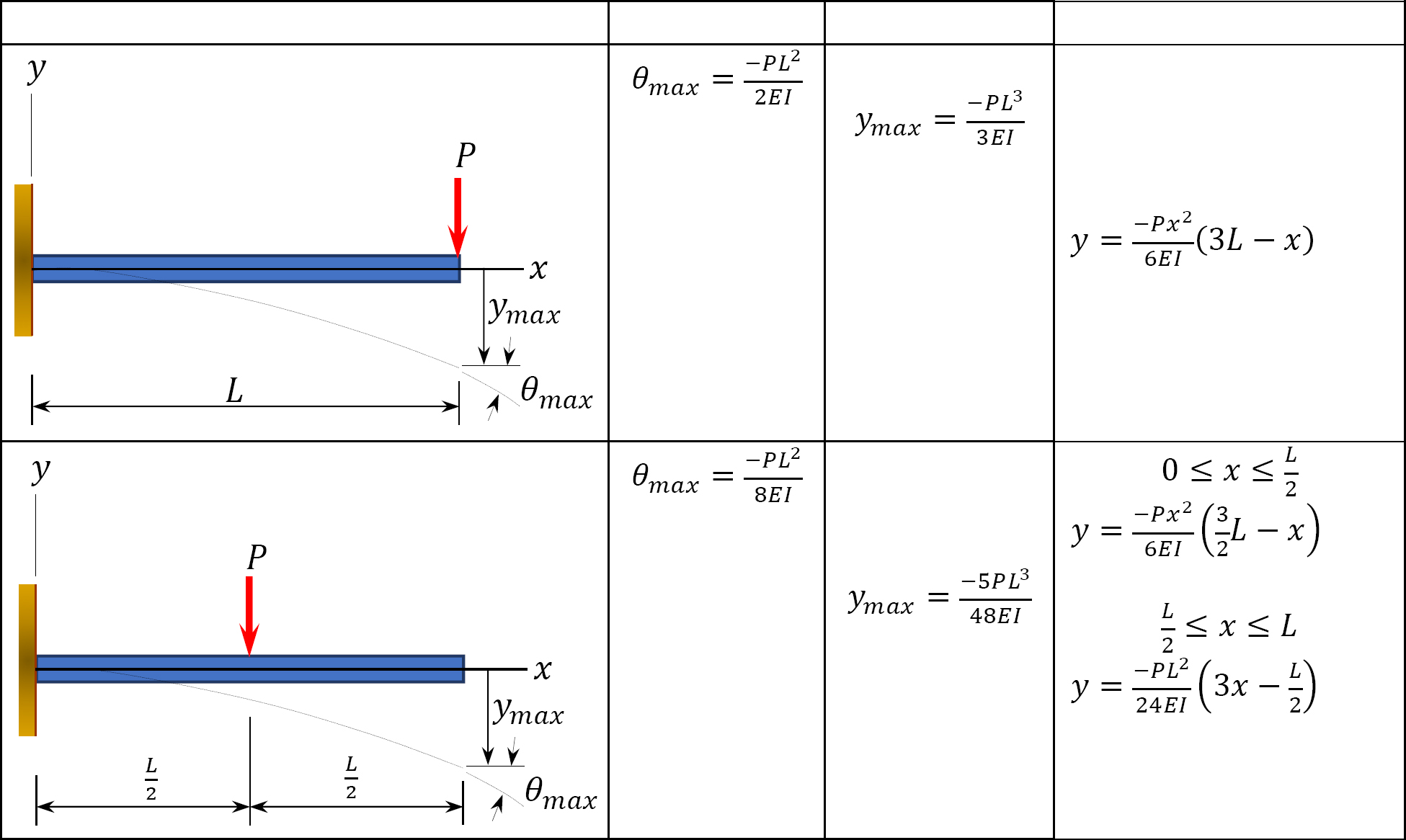
10.3.3 Use of Beam-Deflection Tables for Computation of Flexibility Coefficients
This is the easiest method of computation of flexibility coefficients. It involves obtaining the constants from tabulated deflections based on the types of supports and loading configurations, as shown in Table 10.1 and Table 10.2.
Table 10.1. Simply supported beam slopes and deflections.

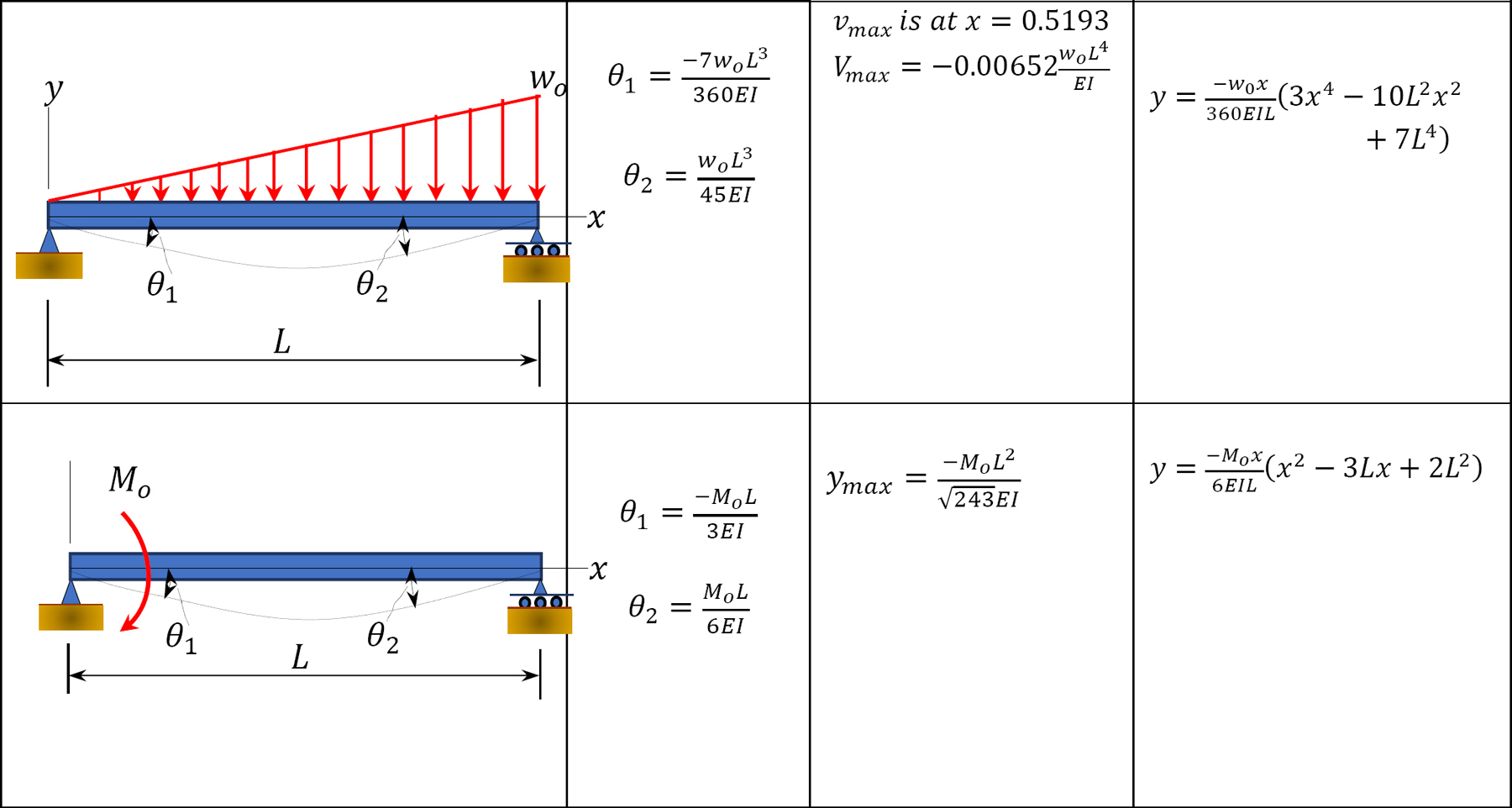
Table 10.2. Cantilevered beam slopes and deflections.
Example 10.4
Draw the bending moment and the shearing force for the indeterminate beam shown in Figure 10.7a. EI = constant.
Solution
Classification of structure. There are four unknown reactions in the beam. Thus, the beam is indeterminate to one degree.
Choice of primary structure. The reaction at B is chosen as the redundant reaction. Thus, the primary structure is a simply supported beam, as shown in Figure 10.7b. Shown in Figure 10.7c and Figure 10.7d are the primary structures loaded with the redundant reactions.
Compatibility equation. The compatibility equation for the beam is written as follows:
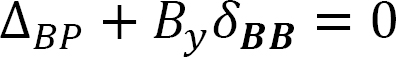
To compute the flexibility coefficients ∆BP and δBB, use the beam-deflection formulas in Table 10.1.
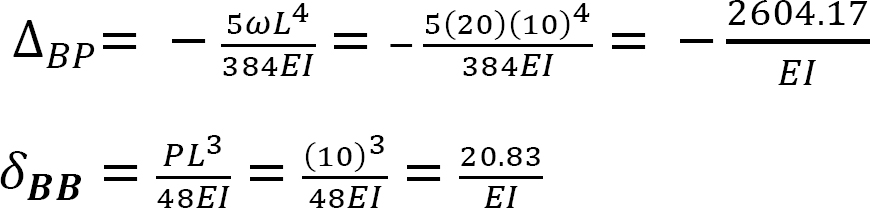
Putting the computed flexibility coefficients into the compatibility equation suggests the following:
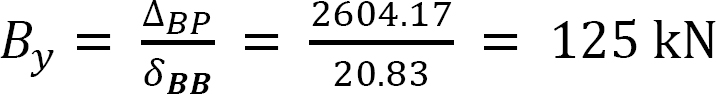
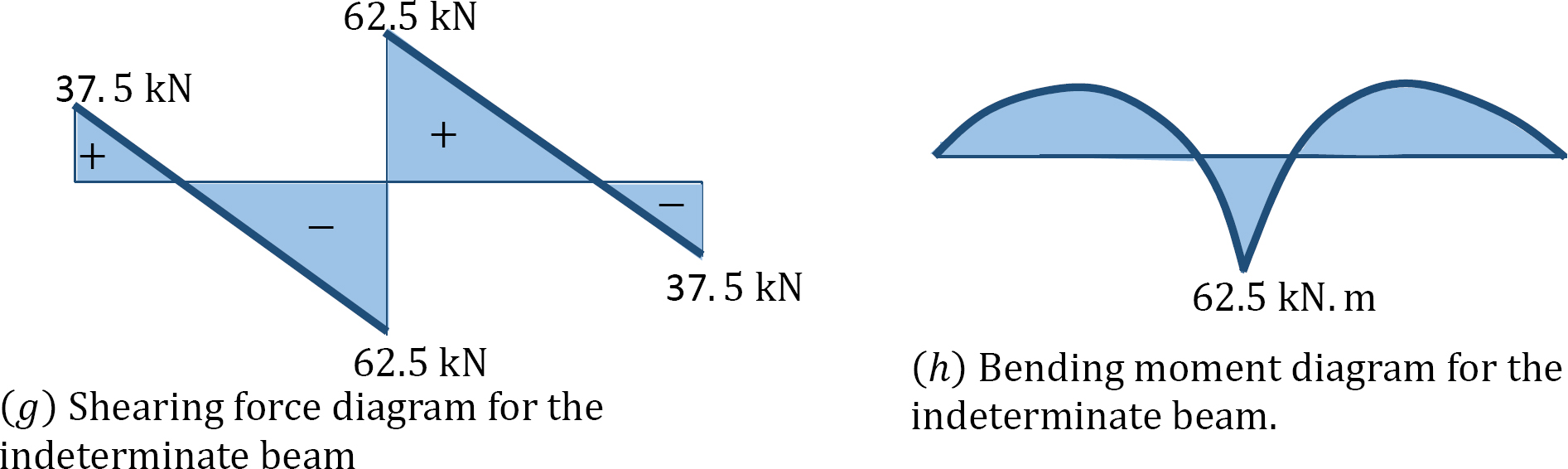
Example 10.5
To obtain the flexibility coefficients, use the beam-deflection tables to determine the support reactions of the beams in examples 10.1 and 10.2.
Solution
Classification of structure. The degree of indeterminacy of the beam in examples 10.1 and 10.2 is 2.
Flexibility coefficients. Using the information in Table 10.2, determine the flexibility coefficients for example 10.1, as follows:
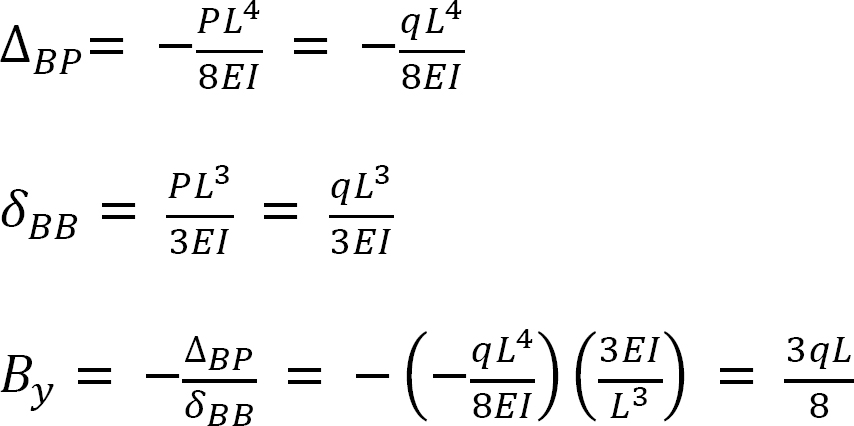
Using the beam-deflection formulas, obtain the following flexibility coefficients for the beam in example 10.2, as follows:
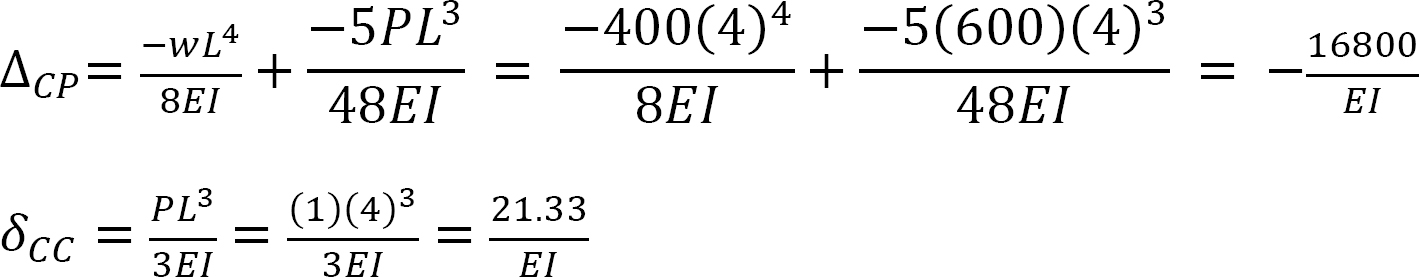
Putting the computed flexibility coefficients into the compatibility equation suggests the following answer:
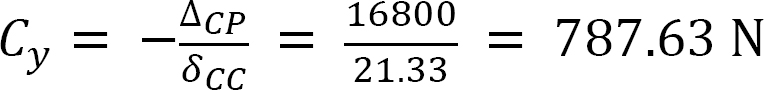
Example 10.6
Using the method of consistent deformation, draw the shearing force and the bending moment diagrams of the frame shown in Figure 10.8a. EI = constant.
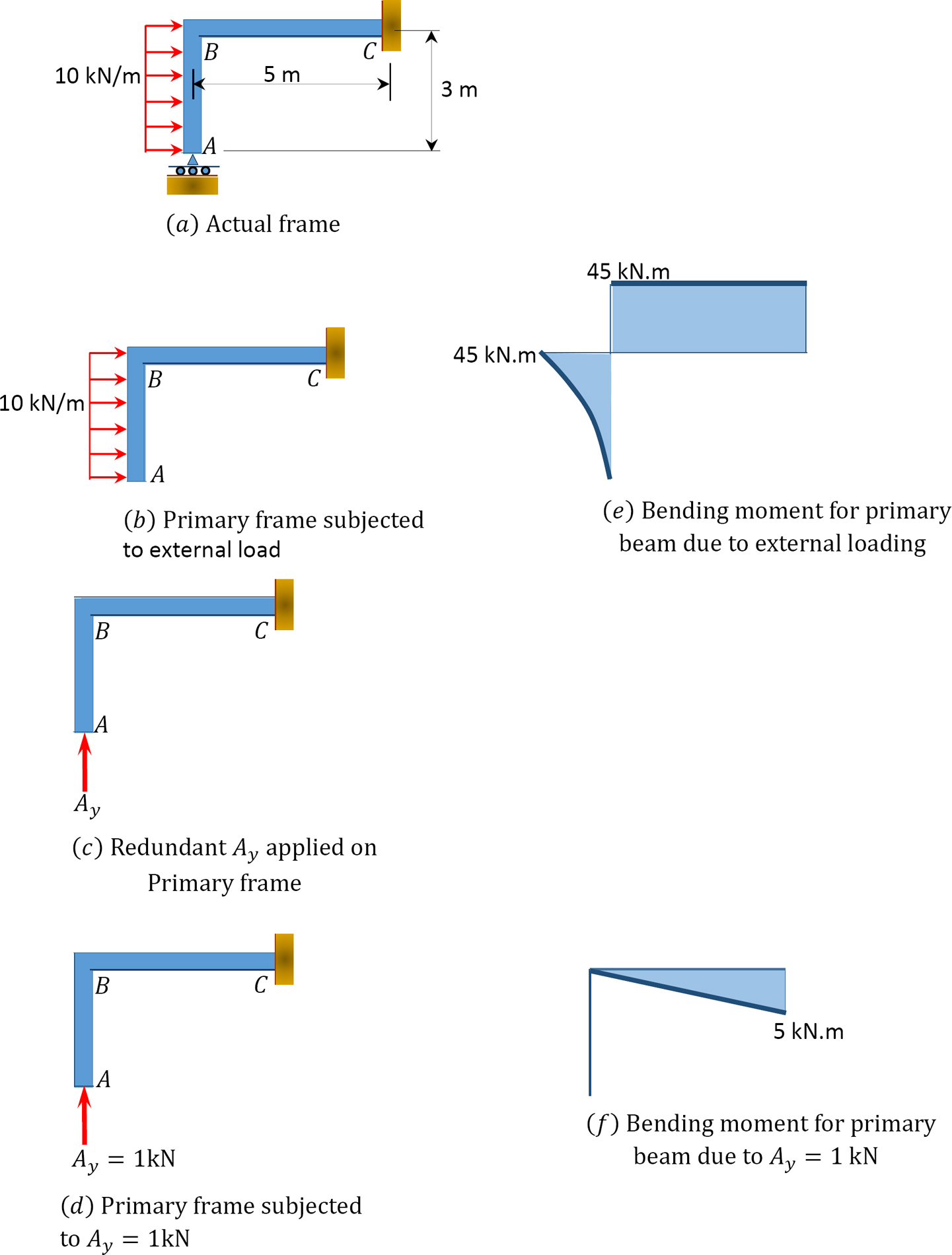
Solution
Classification of structure. There are four unknown reactions in the frame: one unknown reaction at the free end A and three unknown reactions at the fixed end C. Thus, the degree of indeterminacy of the structure is one.
Choice of primary structure. Selecting the reaction at support A as the redundant unknown force suggests that the primary structure is as shown in Figure 10.8b. The primary structure loaded with the redundant force is shown Figure 10.8c and Figure 10.8d.
Compatibility equation. The compatibility equation for the indeterminate frame is as follows:
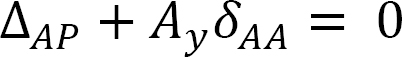
The flexibility or compatibility coefficients ∆AP and δAA are computed by graph multiplication method, as follows:
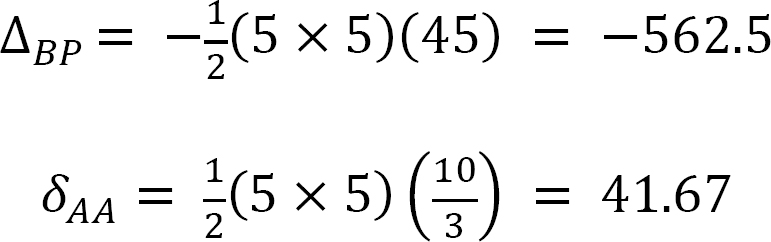
Substituting the flexibility coefficients into the compatibility equation and solving it to obtain the redundant reaction suggests the following:
–562.5 + 41.67Ay = 0
Ay = 13.5 kN
Determining the reactions at C.
∑ MC = 0: –(13.5)(5) + (10 × 3)(1.5) + MC = 0
MC = 22.5.6 kN. m
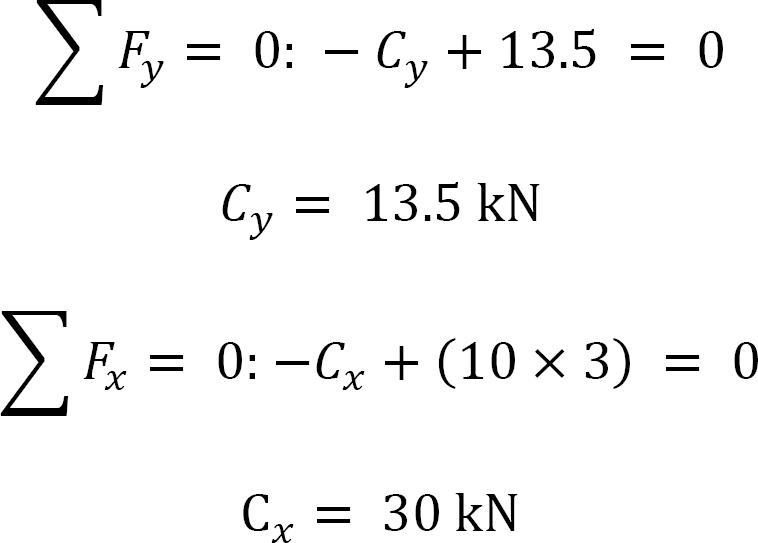
Example 10.7
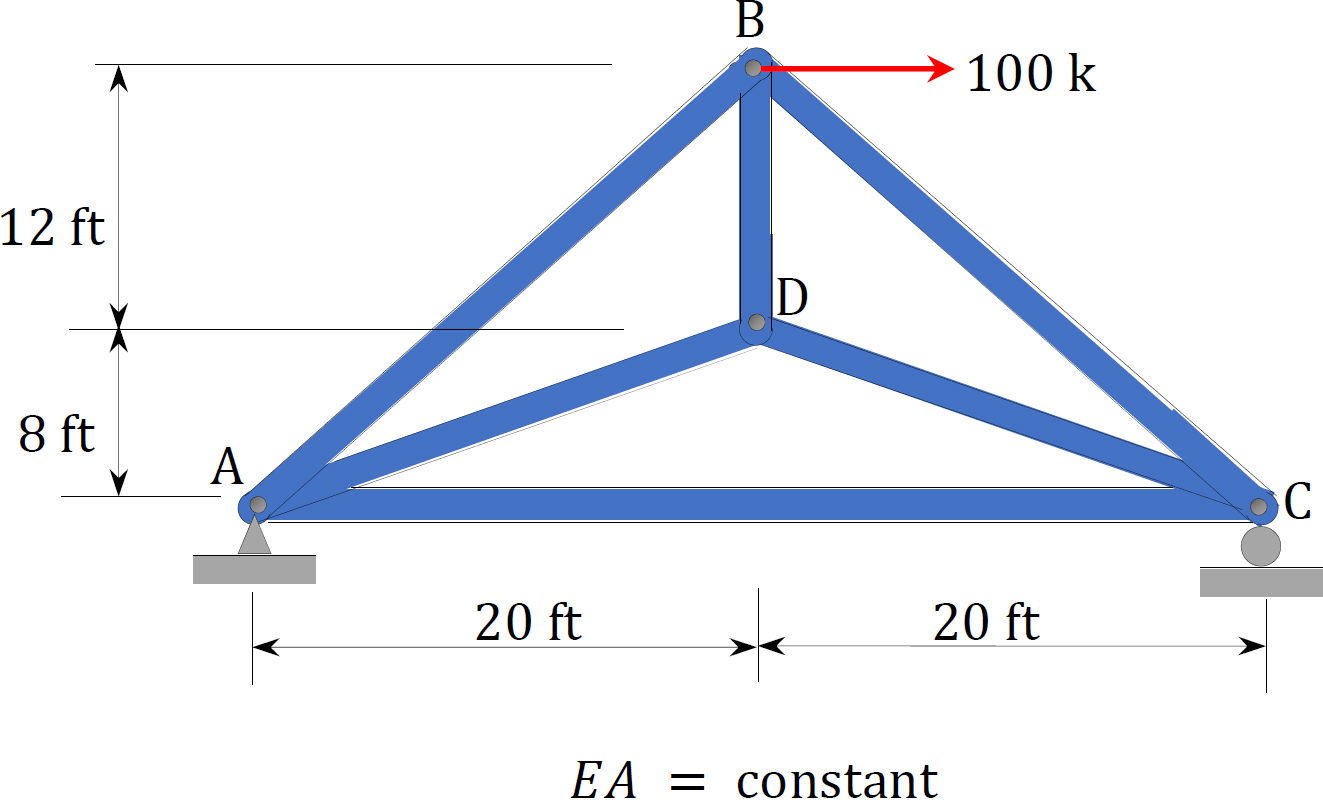
Using the method of consistent deformation, determine the support reactions of the truss shown in Figure 10.9a. EI = constant.
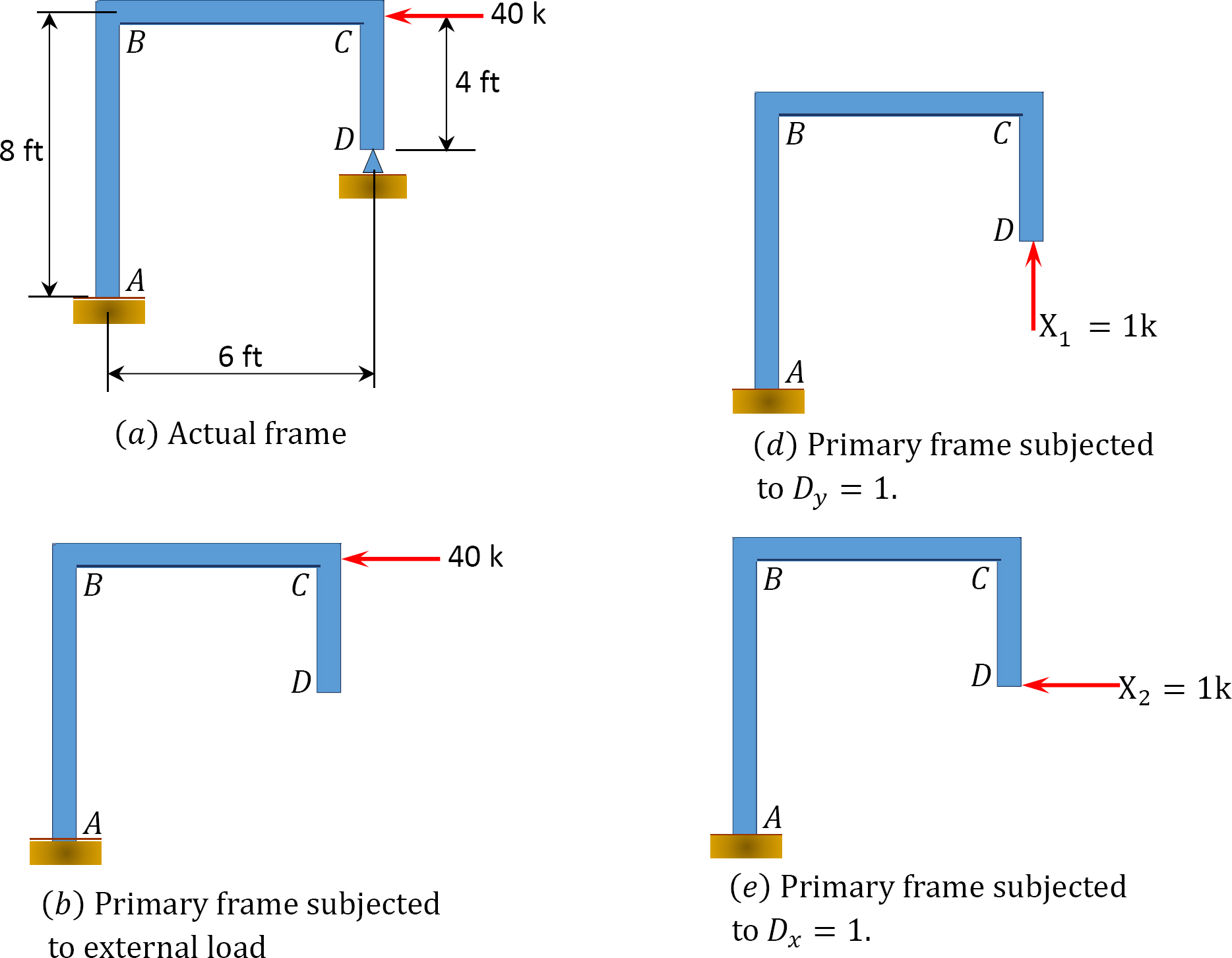

Solution
Classification of structure. There are five unknown reactions in the beam. Thus, the degree of indeterminacy of the structure is two.
Choice of primary structure. The two reactions of the pin support at D are chosen as the redundant reactions, therefore the primary structure is a cantilever beam subjected to a horizontal load at C, as shown in Figure 10.9b. The primary structure loaded with the redundant unknowns is shown in Figure 10.9d and Figure 10.9e.
Compatibility equation. The number of compatibility equations is two, since there are two redundant unknowns. The equations are written as follows:
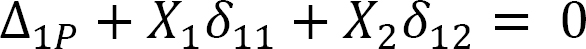
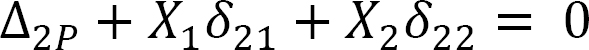
The first number of the subscript in the flexibility coefficients indicates the direction of the deflection, while the second number or letter indicates the force causing the deflection. The coefficients are computed using the graph multiplication method, as follows:

Substituting the flexibility coefficients into the compatibility equation suggests the following two equations with two unknowns:
7680 + 360X1 – 72X2 = 0
1707.76 – 72X1 + 160.08X2 = 0
Solving both equations simultaneously suggests the following:
X1 = Dy = 25.79k
X2 = Dx = 22.27k
Determination of the reactions at support A.
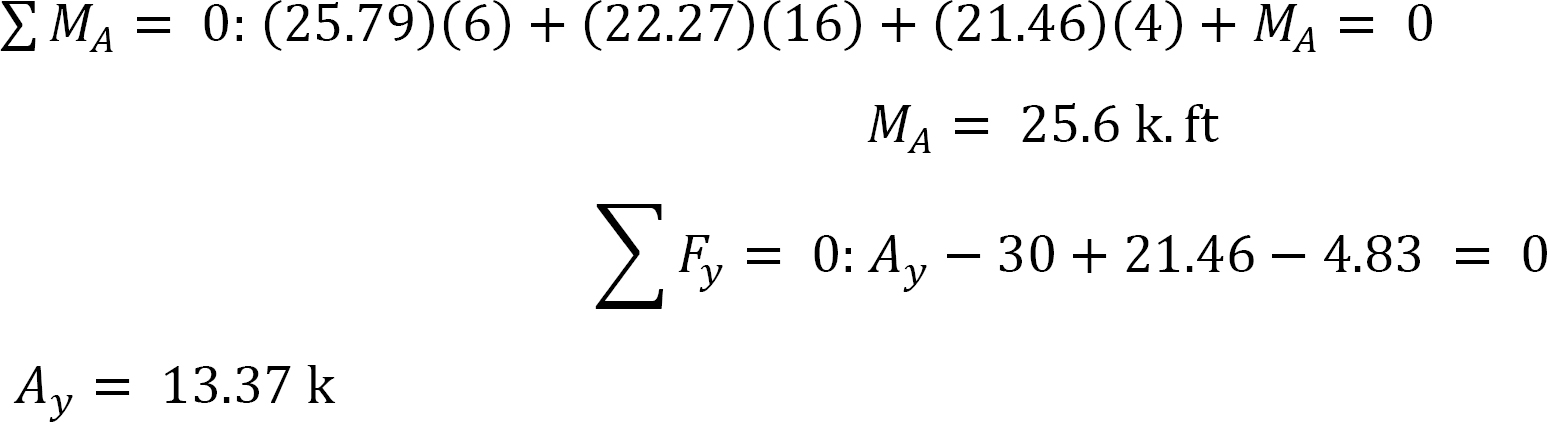
10.4 Analysis of Indeterminate Trusses
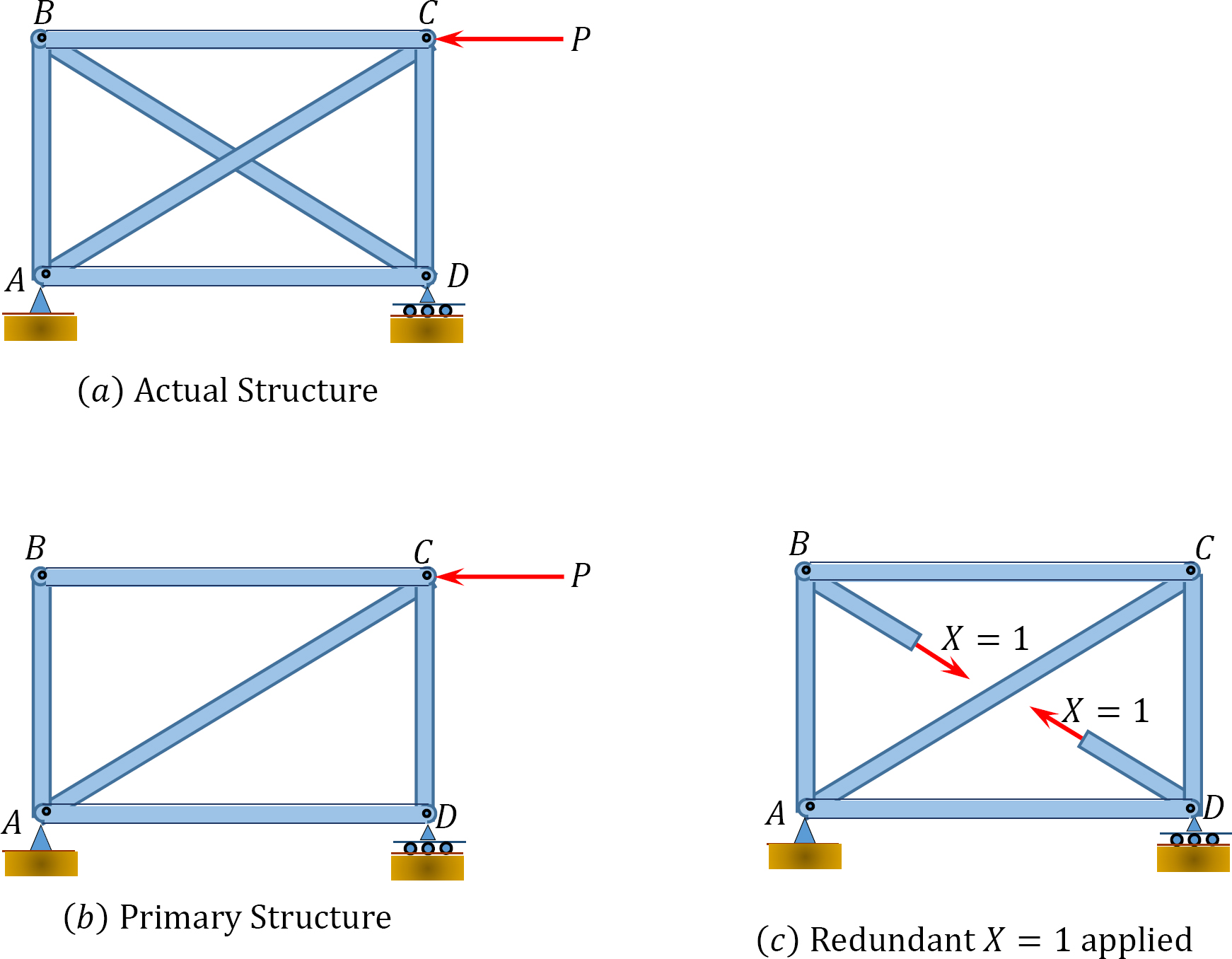
The procedure for the analysis of indeterminate trusses is similar to that followed in the analysis of beams. For trusses with external redundant restraints, the procedure entails determining the degree of indeterminacy of the structure, selecting the redundant reactions, writing the compatibility equations, determining the deflection due to the applied load and the one due to a unit redundant reaction force applied to the primary structure, and solving the compatibility equation(s) to determine the redundant reactions. For trusses with internal redundant members, the procedure involves selecting the redundant members, cutting the redundant members and depicting each of them as a pair of forces in the primary structure, and then applying the condition of compatibility to determine the axial forces in the redundant members. Consider the truss below for an example. This truss is indeterminate to the first degree. Members AC and BD of the truss are two separate overlapping members. Either of these members can be considered redundant, since the primary structure obtained after the removal of either of them will remain stable. Selecting BD as the redundant member, cutting through it and applying a pair of forces on the cut surface, and then indicating that the displacement of the truss at the cut surface is zero suggests the following compatibility expression:

where
∆BD = the relative displacement of the cut surface due to the applied load.
δBD = the relative displacement of the cut surface due to an applied unit redundant load on the cut surface.
The flexibility coefficients for the compatibility equation for the indeterminate truss analysis is computed as follows:

where
∆XP = the displacement at a joint X or member of the primary truss due to applied external load.
δX1 = the displacement at joint X or member of the primary truss due to the unit redundant force.
F = axial force in the truss members due to the applied external load that causes the displacement ∆.
f = axial forces in truss members due to the applied unit redundant load that causes the displacement δ.
L = length of member.
A = cross sectional area of a member.
Example 10.8
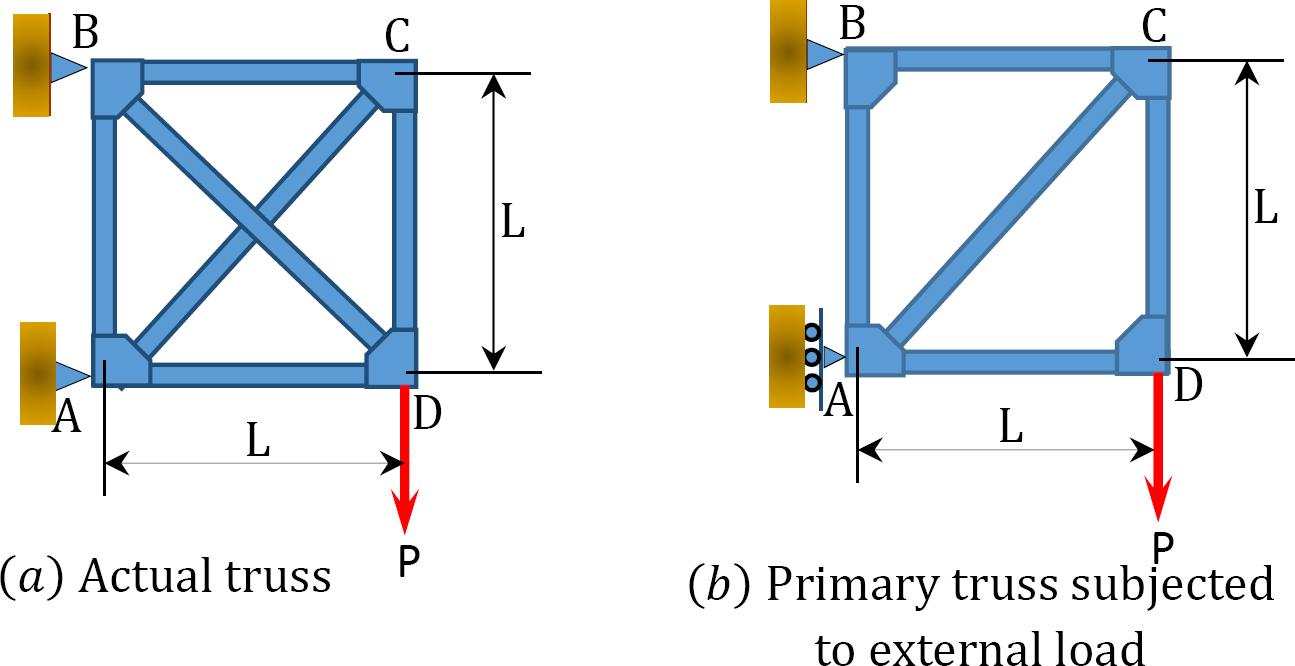
Using the method of consistent deformation, determine the axial force in all the members of the truss shown in Figure 10.11a. EA = constant. .
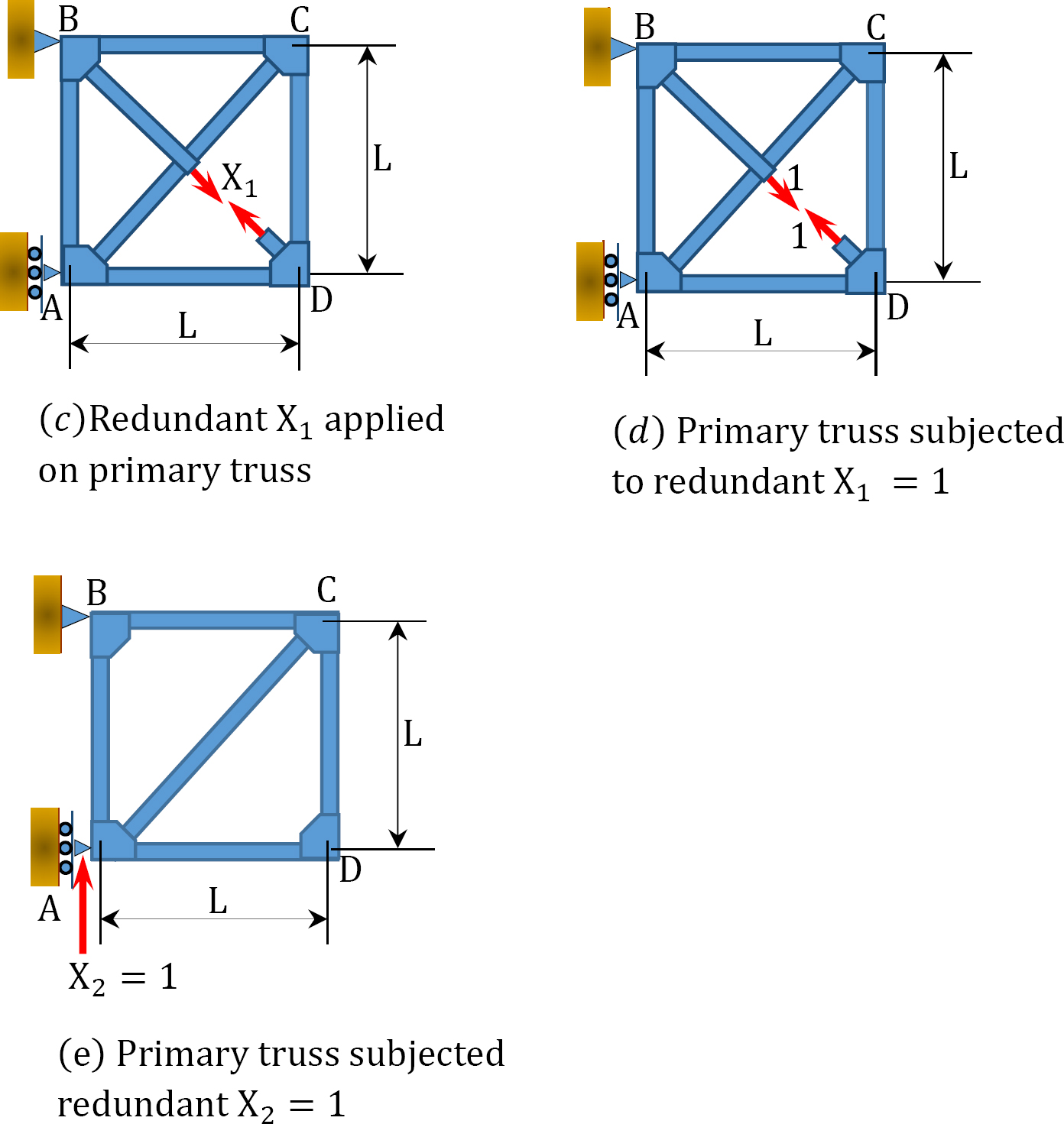
Solution
Determining support reactions in the primary structure.
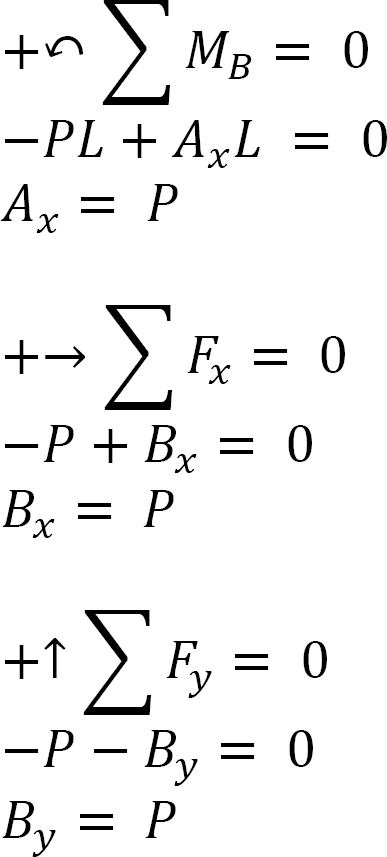
Compatibility Equation.
∆1P + X1δ11 + X2δ12 = 0
∆2P + X1δ21 + X2δ22 = 0
Determining forces in members due to applied external load.
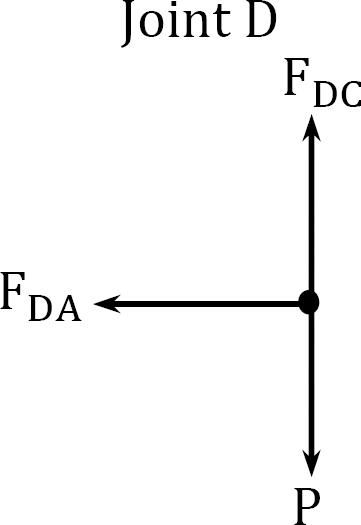
Joint D.
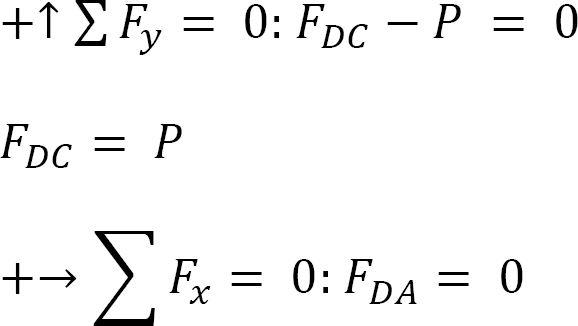
Joint A.
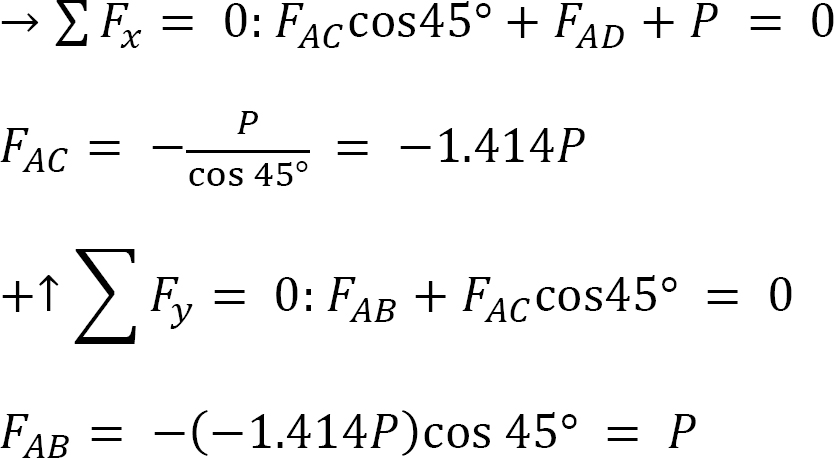
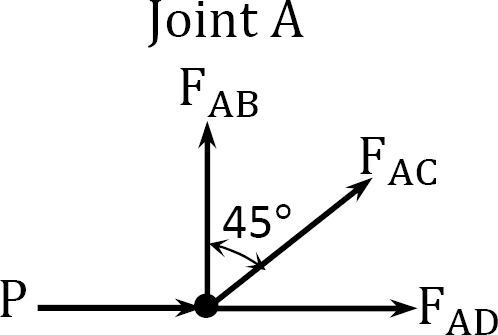
Joint B.
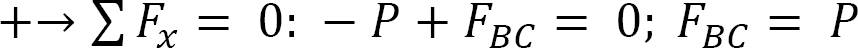
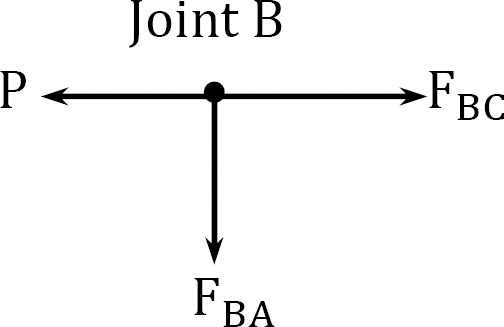
Determining forces in members due to redundant FBD = 1.
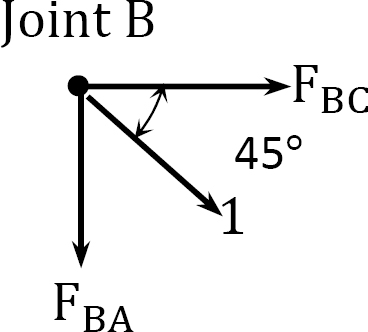
Joint B.
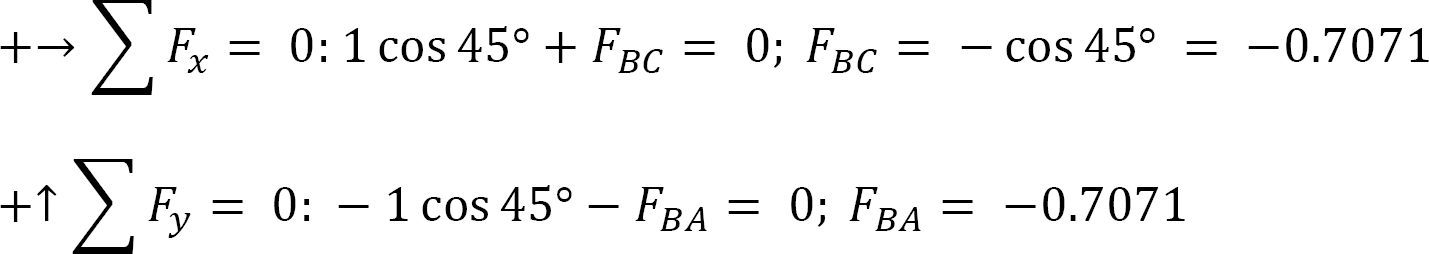
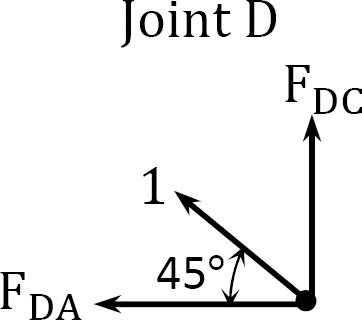
Joint D.
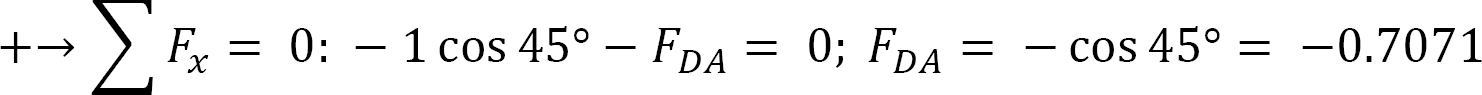
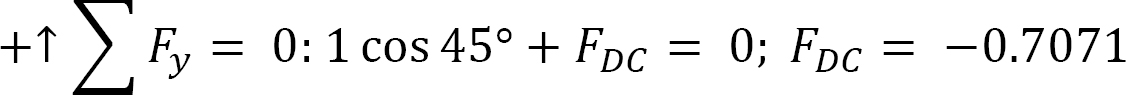
Joint C.

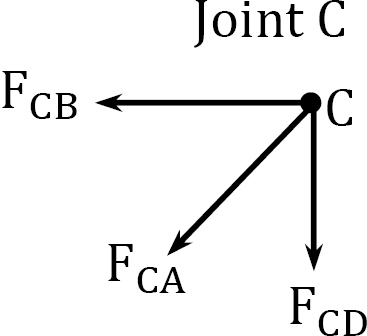
Determining forces in members due to redundant Ay = 1.
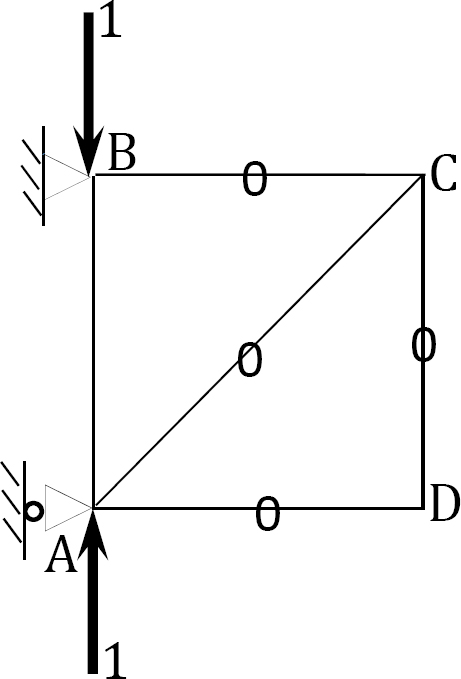
Joint A.

The determination of the member-axial forces can be conveniently performed in a tabular form, as shown in Table 10.3.
Table 10.3.
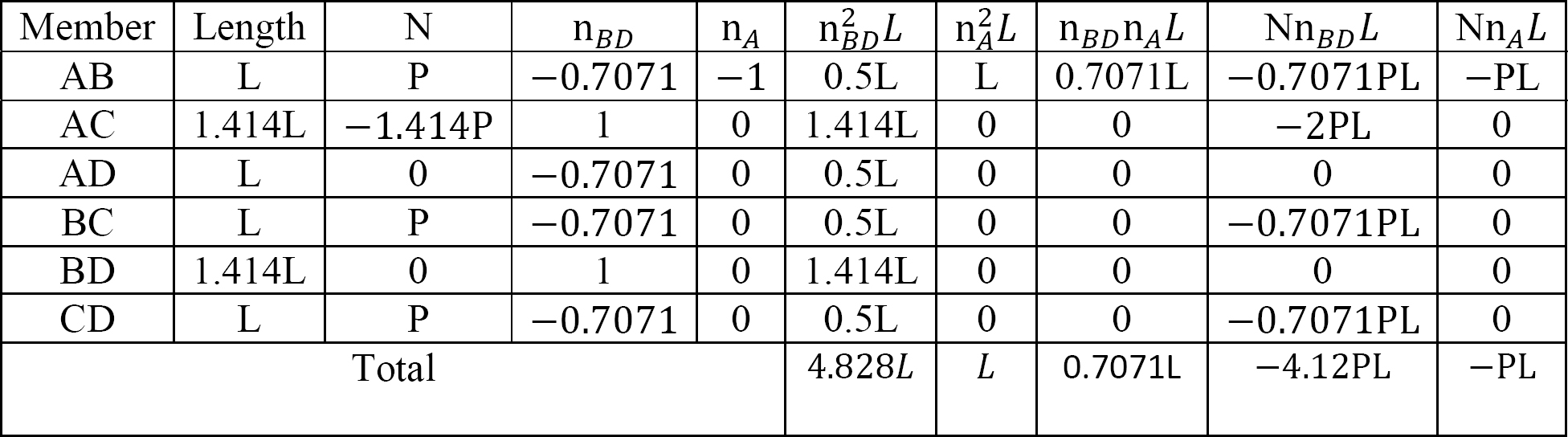
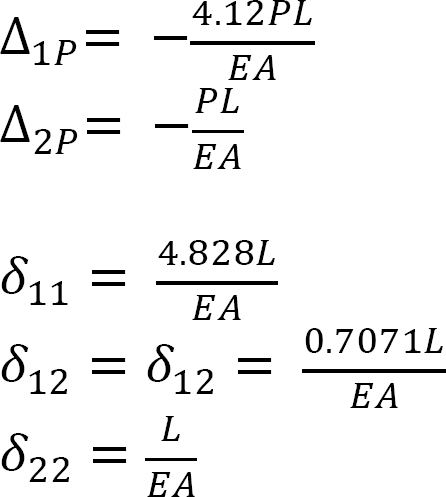
Substituting the flexibility coefficient into the compatibility equations and solving the simultaneous equations suggests the following:
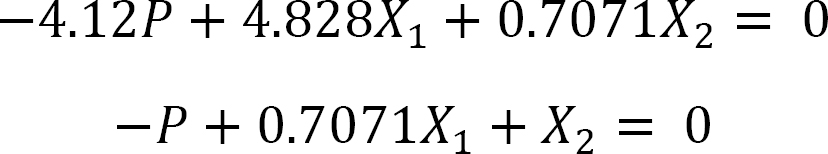
X1 = FBD = 0.79P
X2 = Ay = 0.44P
The axial forces in members are as follows:
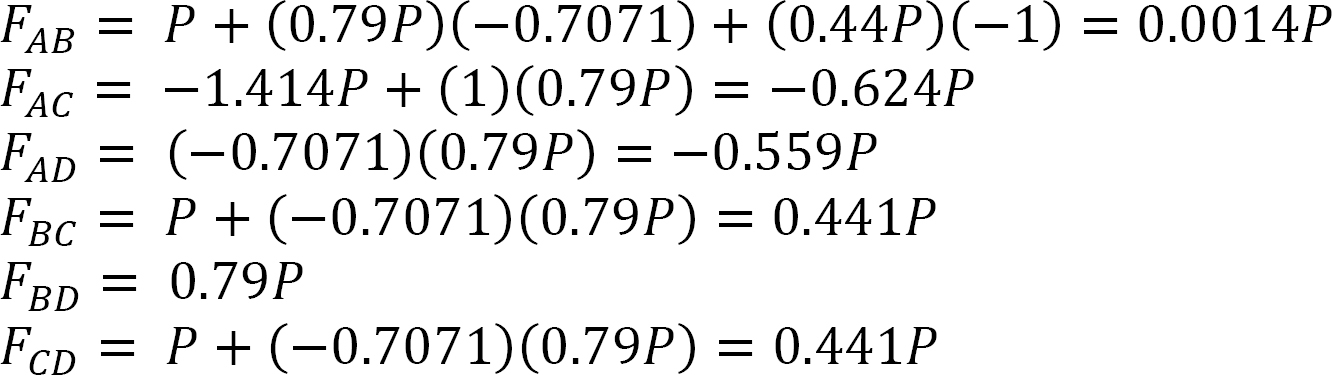
Example 10.9
Using the method of consistent deformation, determine the axial force in member AD of the truss shown in Figure 10.12a. EA = constant.
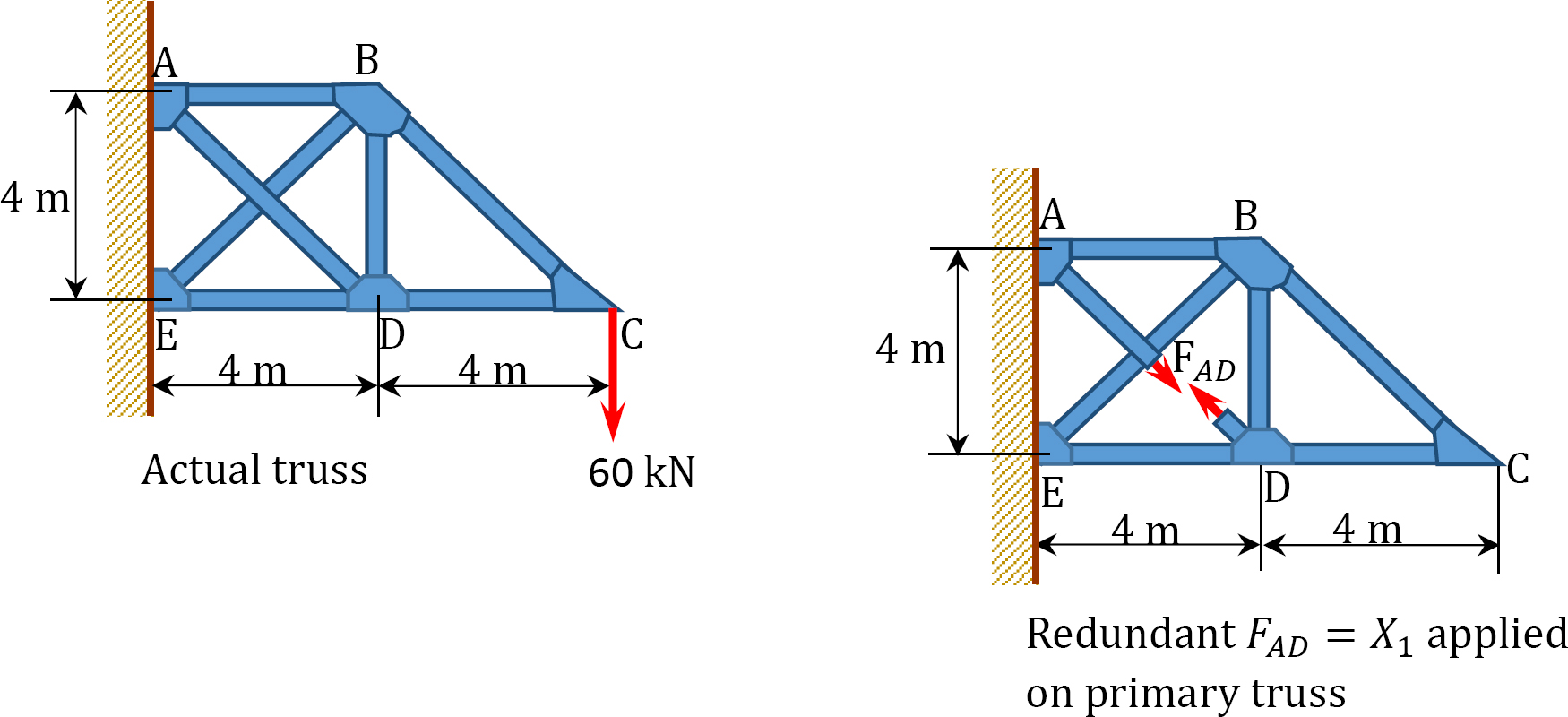
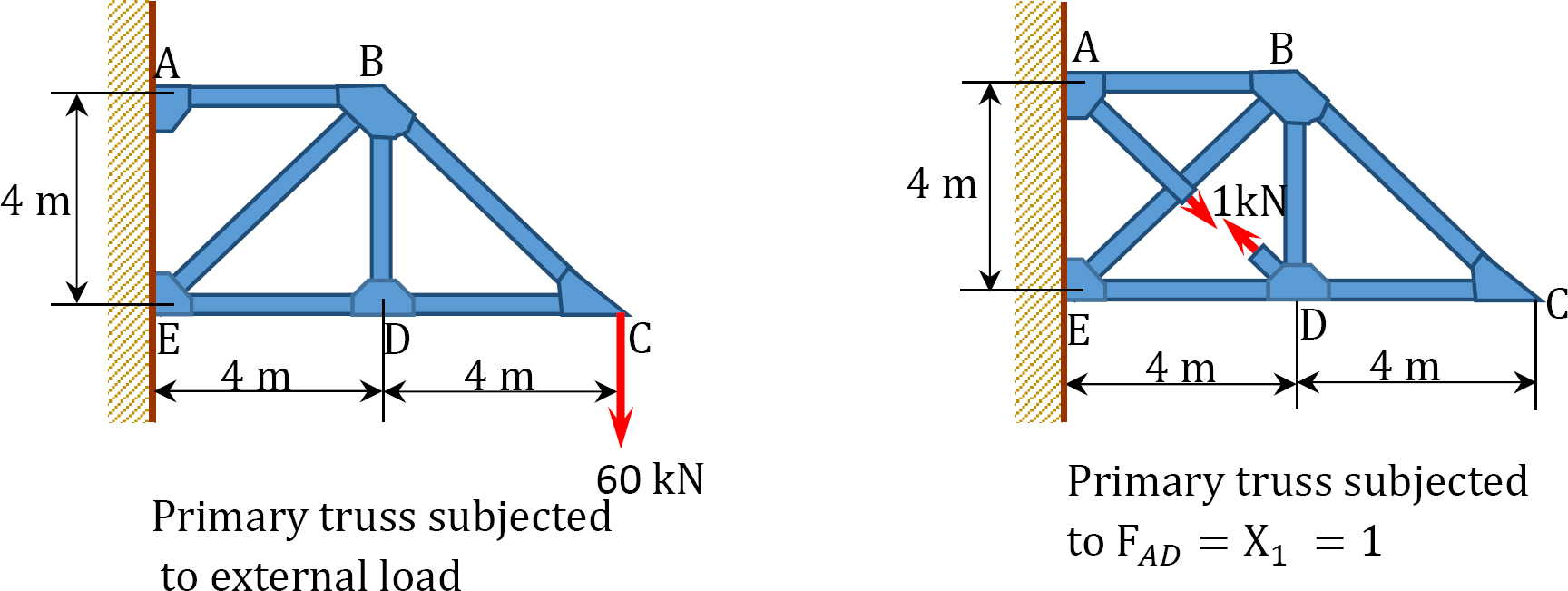
Solution
Determination of axial forces in members due to applied external loads.
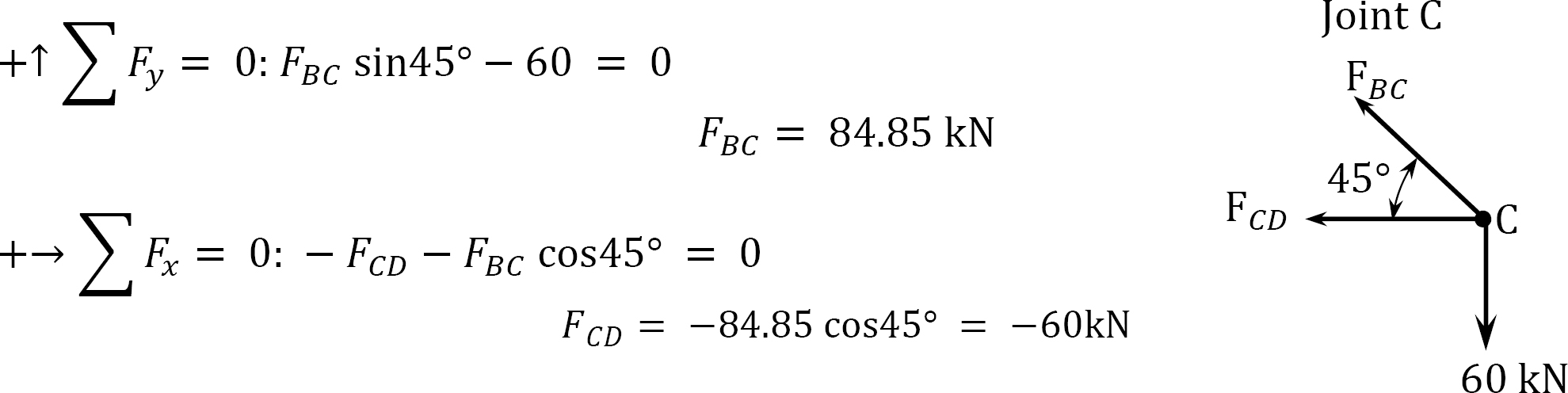
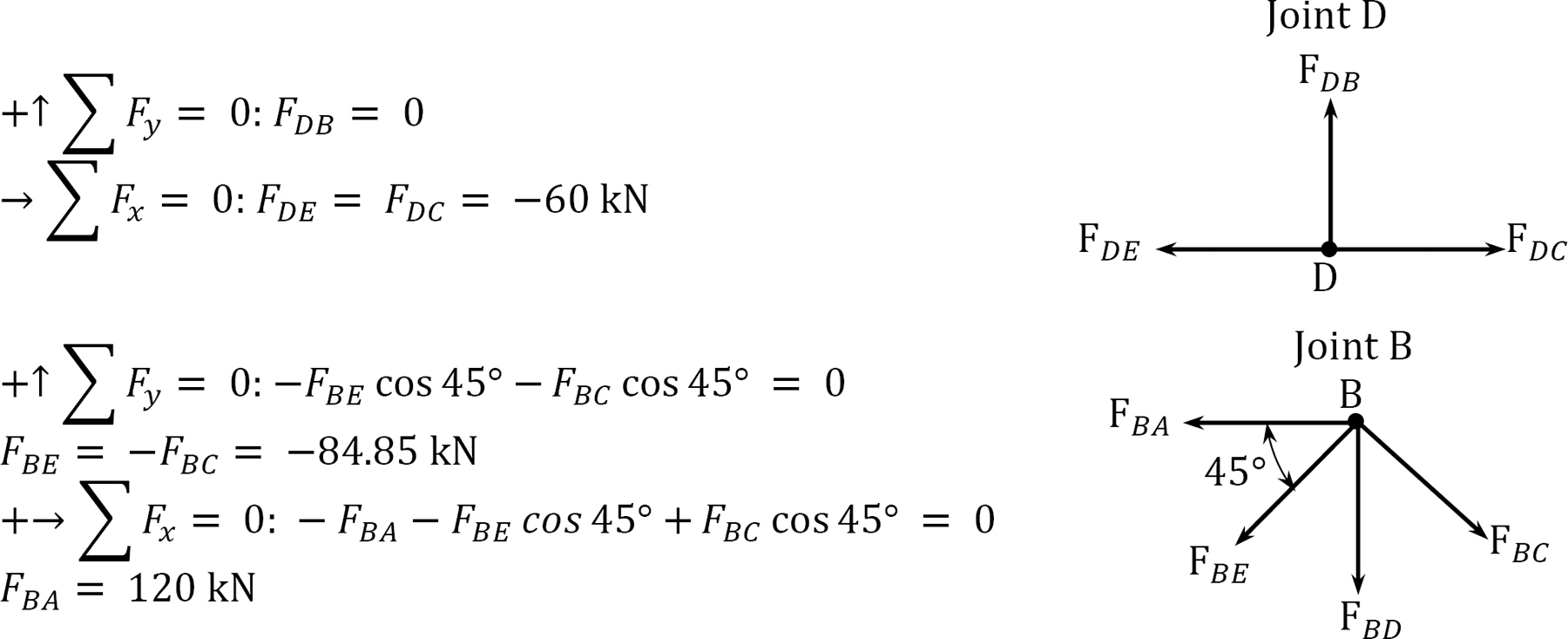
Determining forces in members due to redundant FAD = 1.
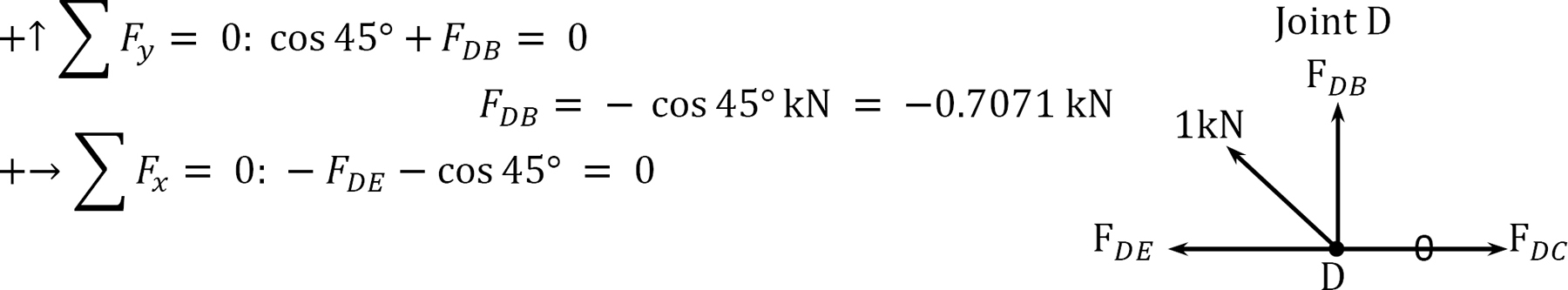
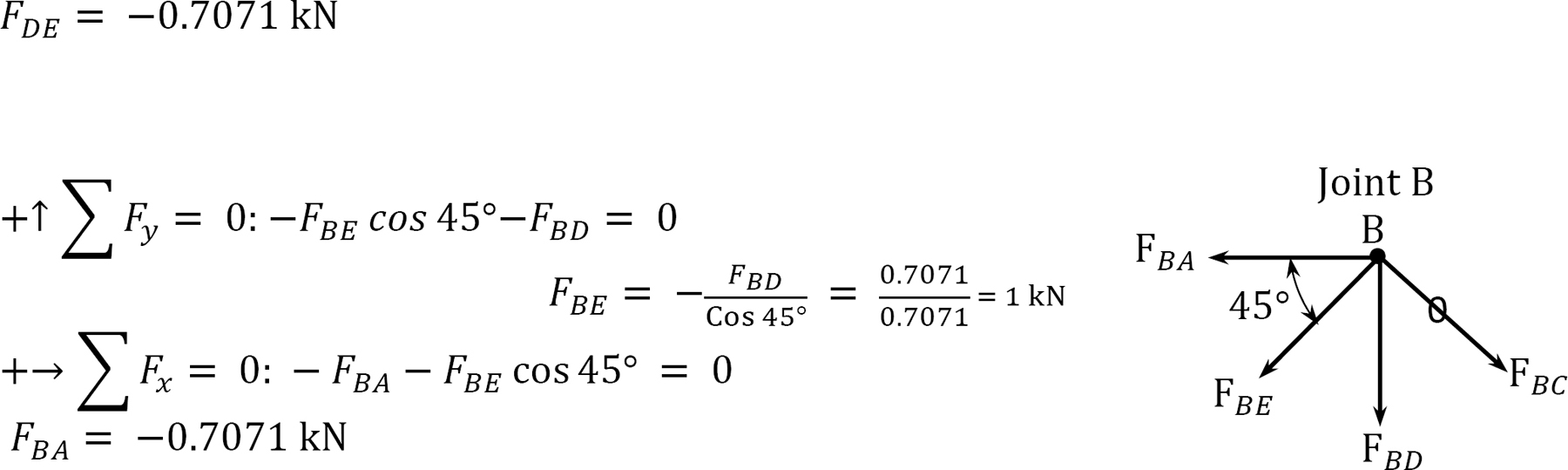
The determination of the member-axial forces can be conveniently performed in a tabular form, as shown in Table 10.4.
Table 10.4.

Compatibility equation.
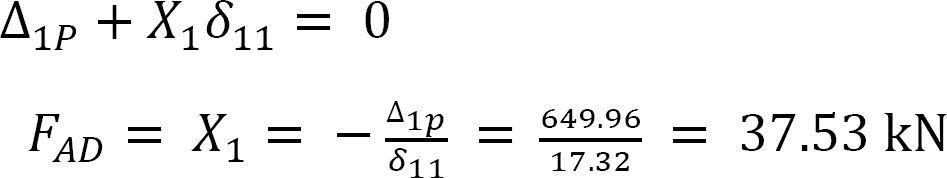
Chapter Summary
Force method: The force method or the method of consistent deformation is based on the equilibrium of forces and compatibility of structures. The method entails first selecting the unknown redundants for the structure and then removing the redundant reactions or members to obtain the primary structure.
Compatibility equations: The compatibility equations are formulated and used together with the equations of equilibrium to determine the unknown redundants. The number of the compatibility equations must match the number of the unknown redundants. Once the unknown redundants are determined, the structure becomes determinate. Methods of computation of compatibility or flexibility coefficients, such as the method of integration, the graph multiplication method, and the use of deflection tables, are solved in the chapter.
Mohr integral for computation of flexibility coefficients for beams and frames:
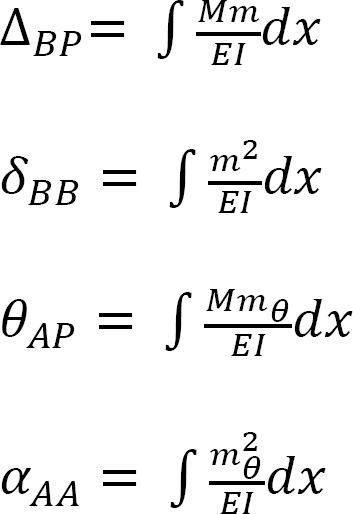
Maxwell-Betti law of reciprocal deflections: The Maxwell-Betti law helps reduce the computational efforts required to obtain the flexibility coefficients for the compatibility equations. This law states that the linear displacement at point A due to a unit load applied at B is equal in magnitude to the linear displacement at point B due to a unit load applied at A for a stable elastic structure. This law is expressed as follows:

Practice Problems
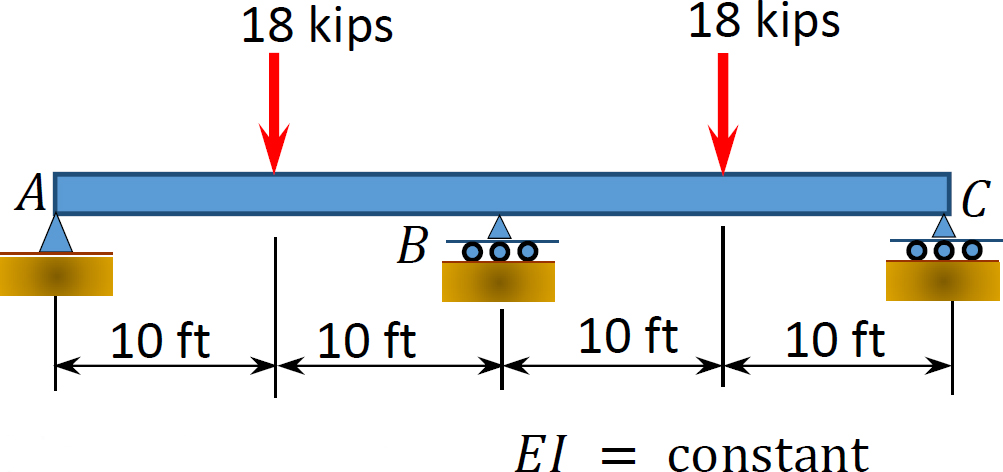
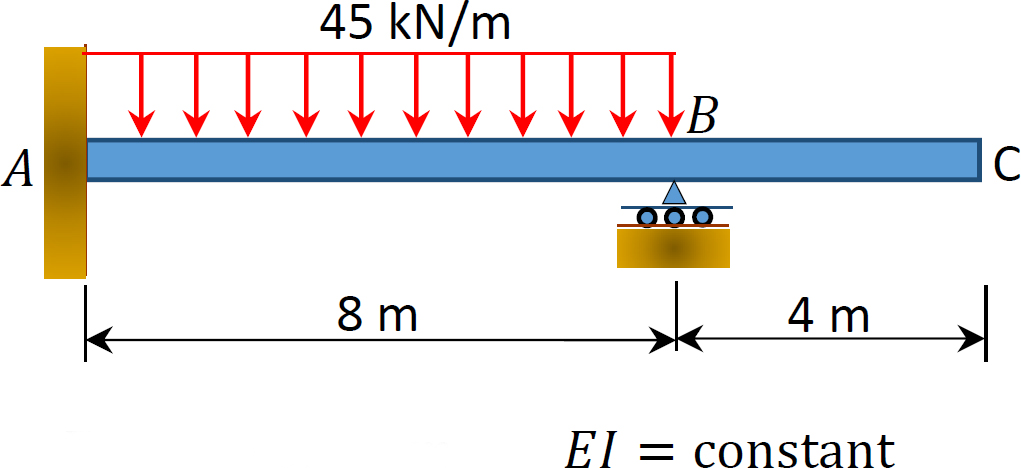
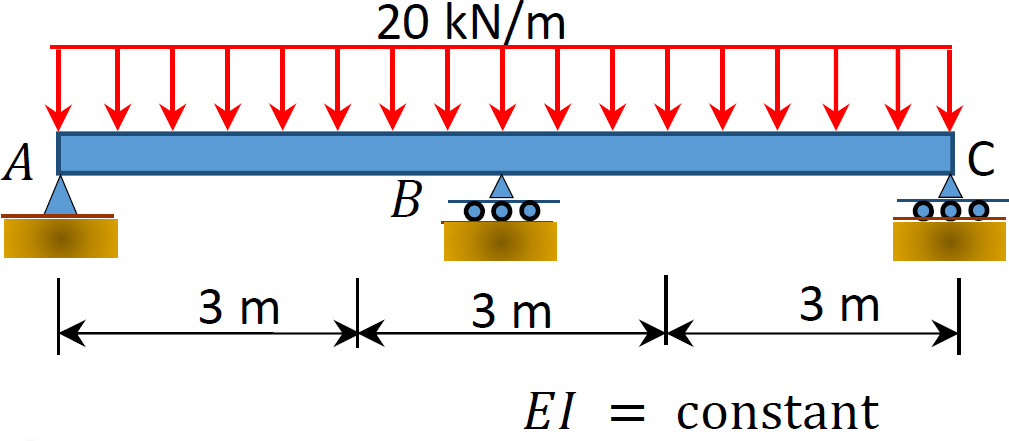
10.1 Using the method of consistent deformation, compute the support reactions and draw the shear force and the bending moment diagrams for the beams shown in Figures P10.1 through P10.4. Choose the reaction at the interior support B as the unknown redundant.

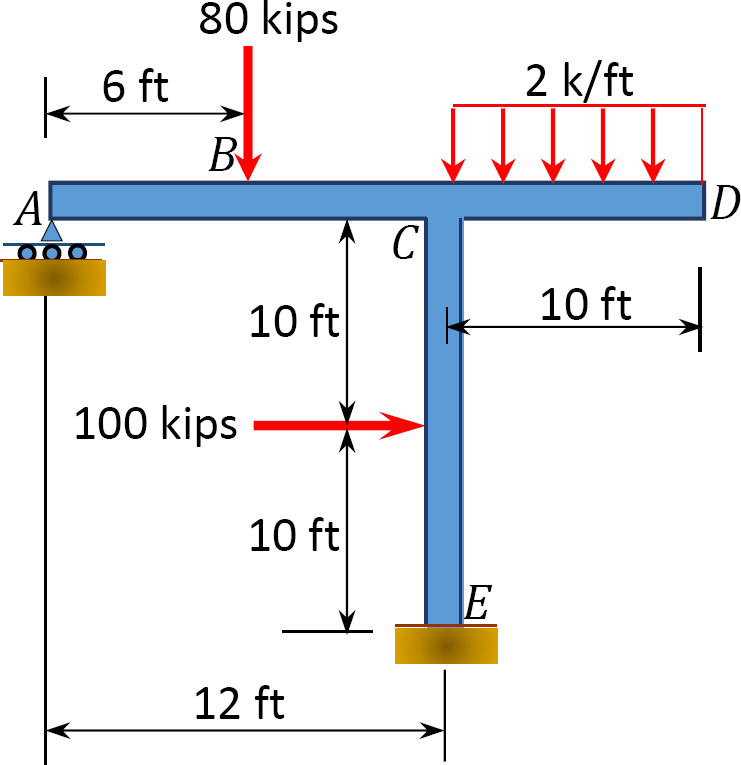
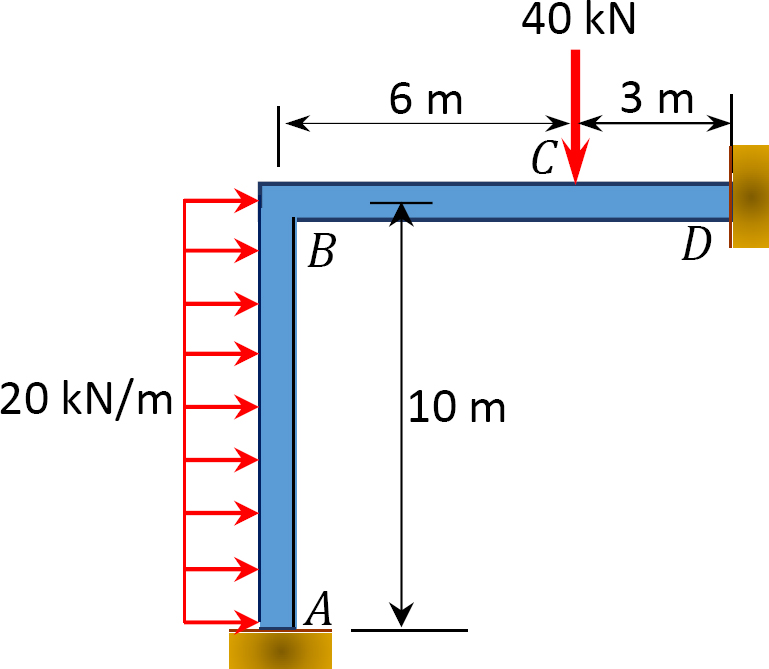
10.2 Using the method of consistent deformation, compute the support reactions and draw the shear force and the bending moment diagrams for the frames shown in Figures P10.5 through P10.8. Choose the reaction(s) at any of the supports as the unknown redundant(s). EI = constant.
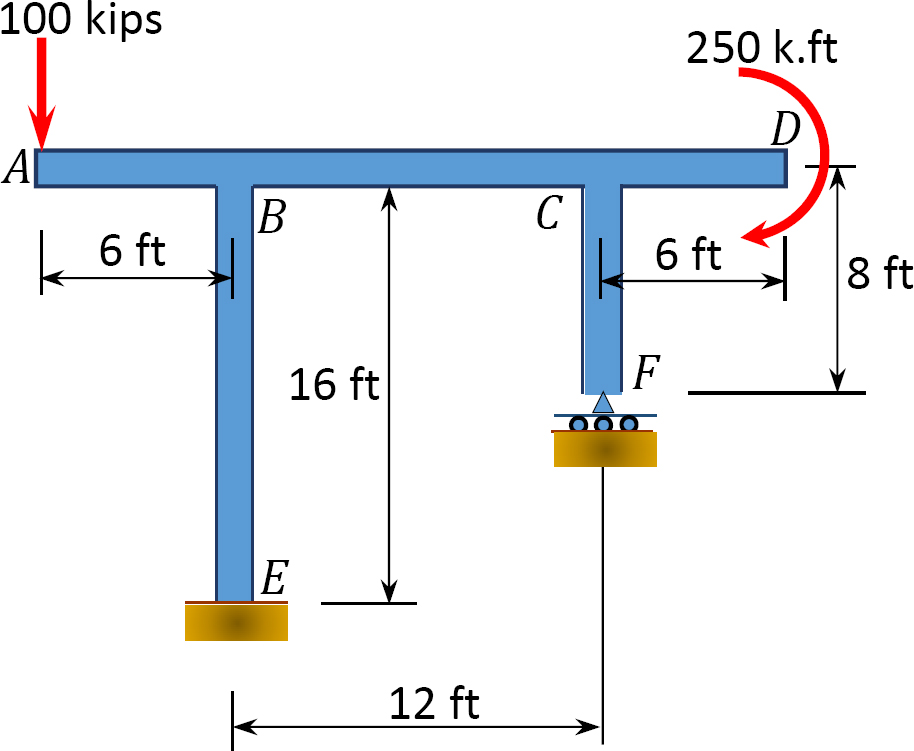
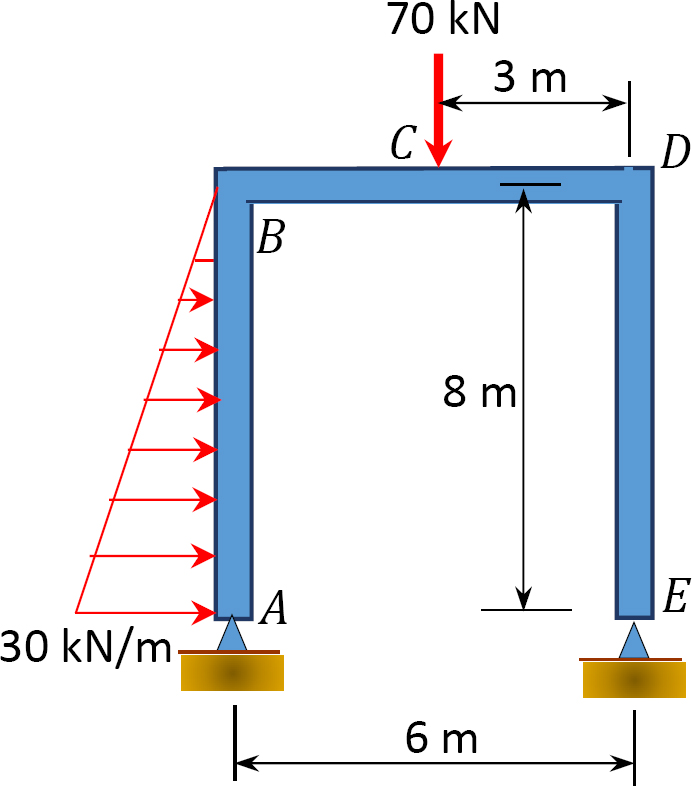
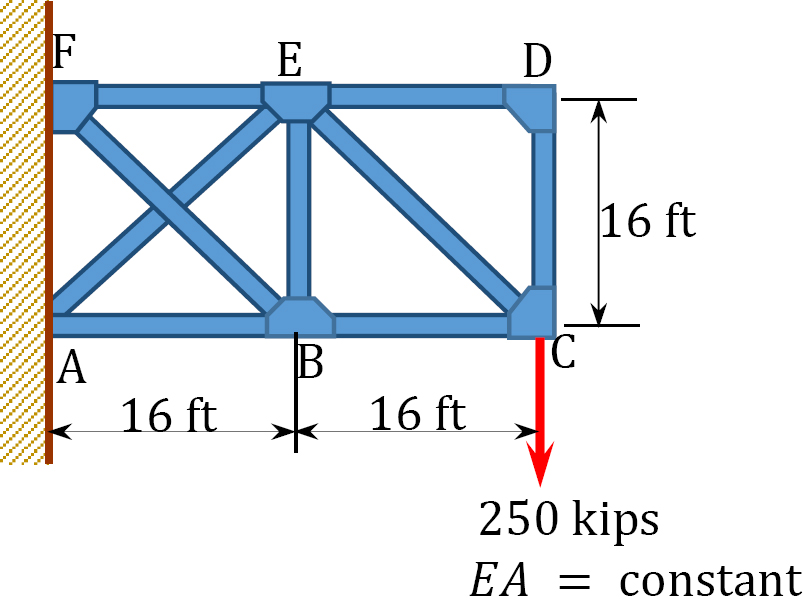
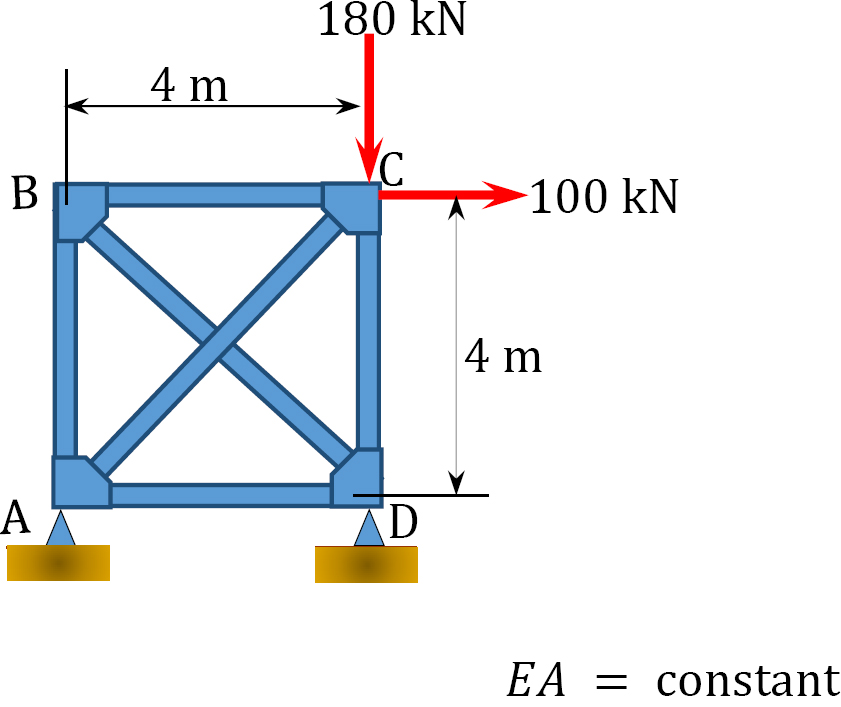
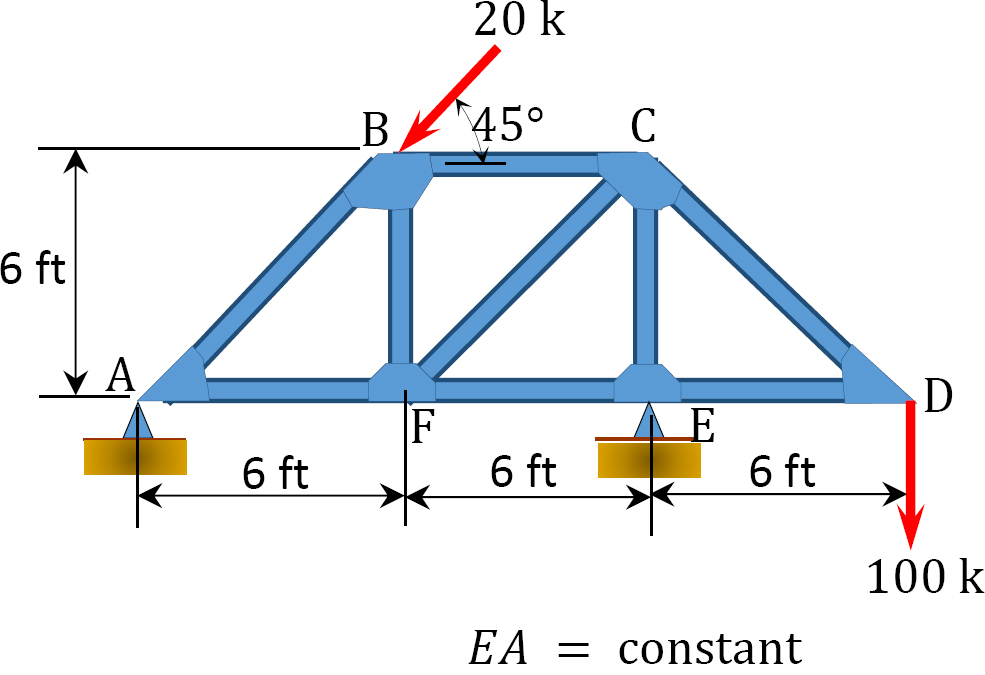
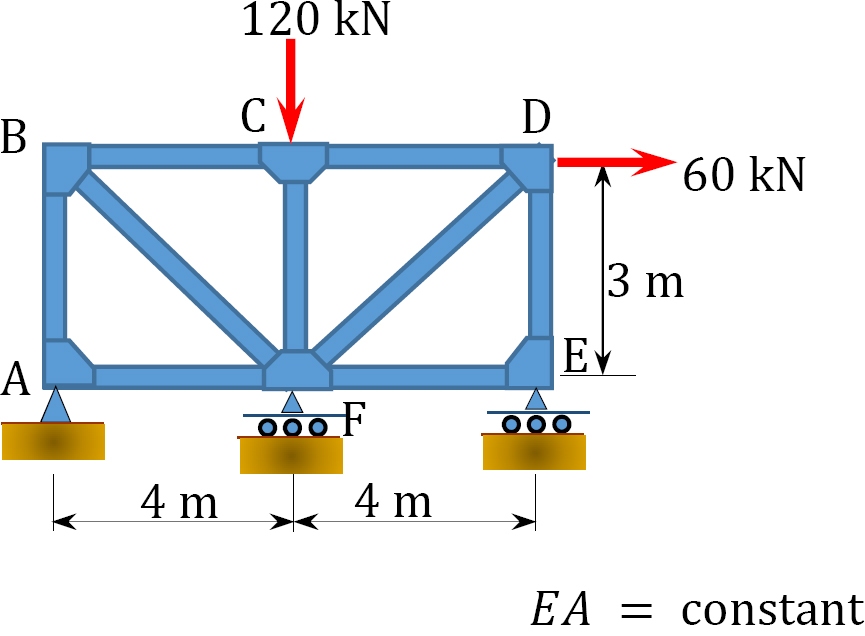
10.3 Using the method of consistent deformations, determine the reactions and the axial forces in the members of the trusses shown in Figures P10.9 through P10.13.