1.11: Slope-Deflection Method of Analysis of Indeterminate Structures
- Page ID
- 17618
Slope-Deflection Method of Analysis of Indeterminate Structures
In 1915, George A. Maney introduced the slope-deflection method as one of the classical methods of analysis of indeterminate beams and frames. The method accounts for flexural deformations, but ignores axial and shear deformations. Thus, the unknowns in the slope-deflection method of analysis are the rotations and the relative joint displacements. For the determination of the end moments of members at the joint, this method requires the solution of simultaneous equations consisting of rotations, joint displacements, stiffness, and lengths of members.
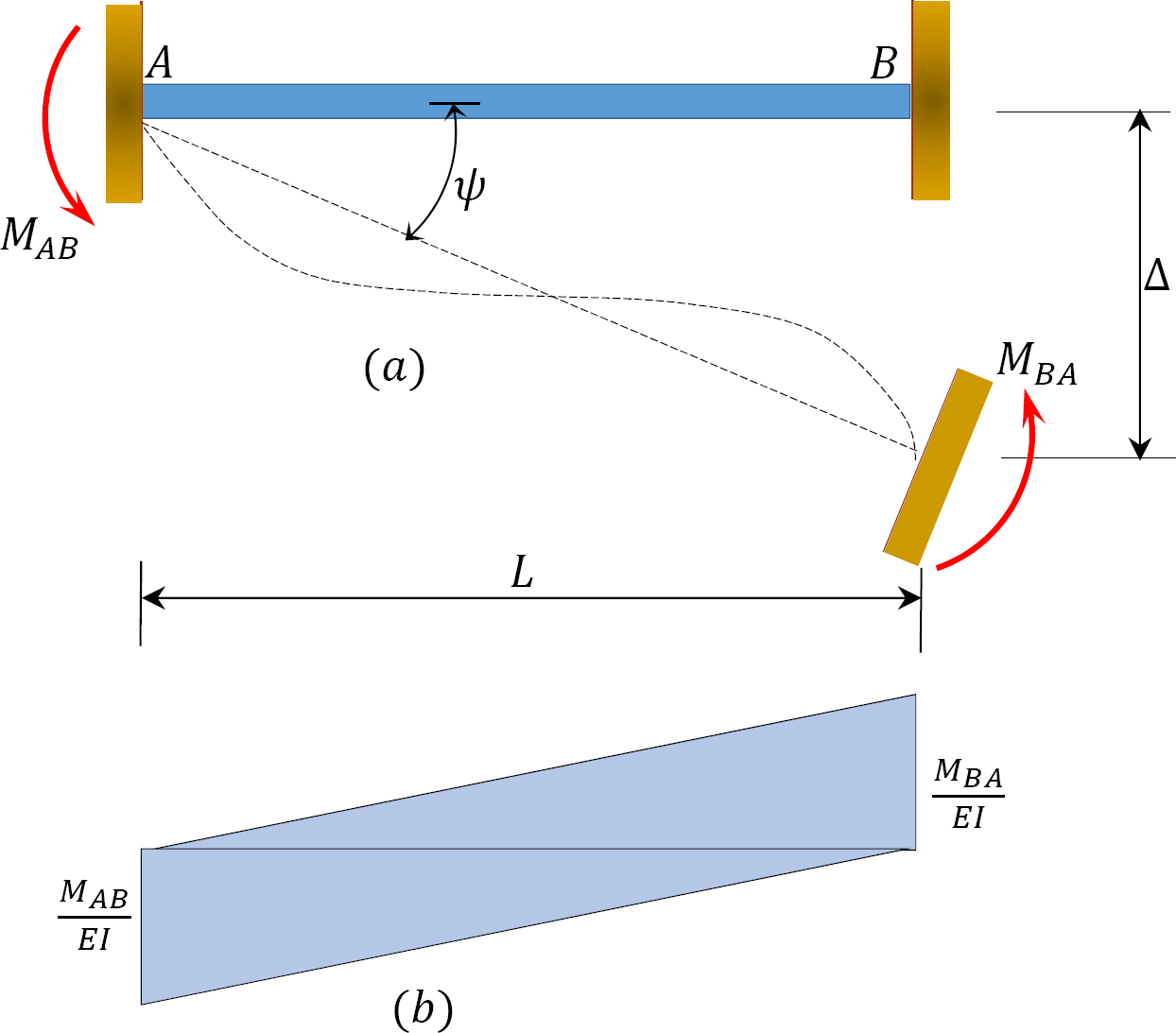
An end moment M is considered positive if it tends to rotate the member clockwise and negative if it tends to rotate the member counter-clockwise. The rotation θ of a joint is positive if its tangent turns in a clockwise direction. The rotation of the chord connecting the ends of a member (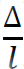 ), the displacement of one end of a member relative to the other, is positive if the member turns in a clockwise direction.
), the displacement of one end of a member relative to the other, is positive if the member turns in a clockwise direction.
11.3 Derivation of Slope-Deflection Equations
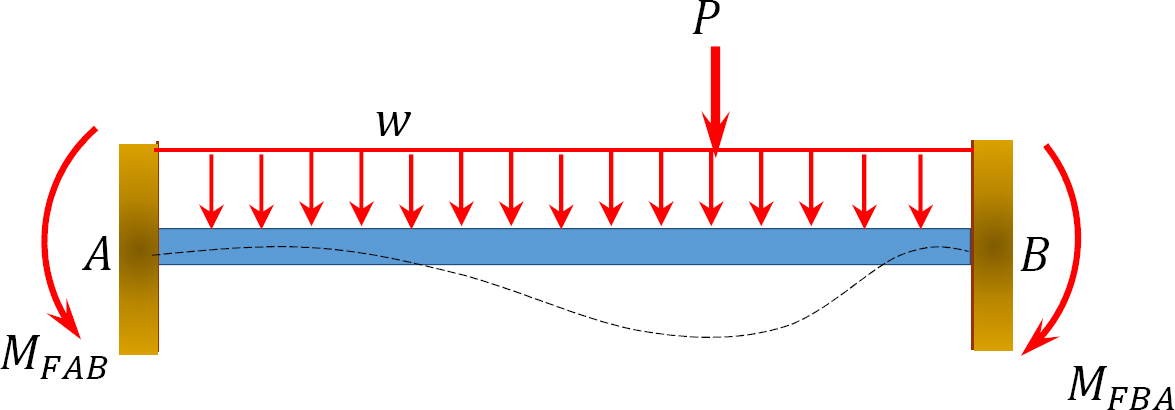
To derive the slope-deflection equations, consider a beam of length L and of constant flexural rigidity EI loaded as shown in Figure 11.1a. The member experiences the end moments MAB and MBA at A and B, respectively, and undergoes the deformed shape shown in Figure 11.1b, with the assumption that the right end B of the member settles by an amount ∆. The end moments are the summation of the moments caused by the rotations of the joints at the ends A and B (θA and θB) of the beam, the chord rotation 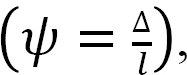 and the fixity at both ends referred to as fixed end moments
and the fixity at both ends referred to as fixed end moments 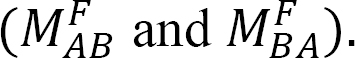
The rotations at the joints of the beam can be expressed mathematically as follows:


where
βA, βB = end rotations caused by moments MAB and MBA, respectively.
ψ = chord rotation caused by settlement of end B.
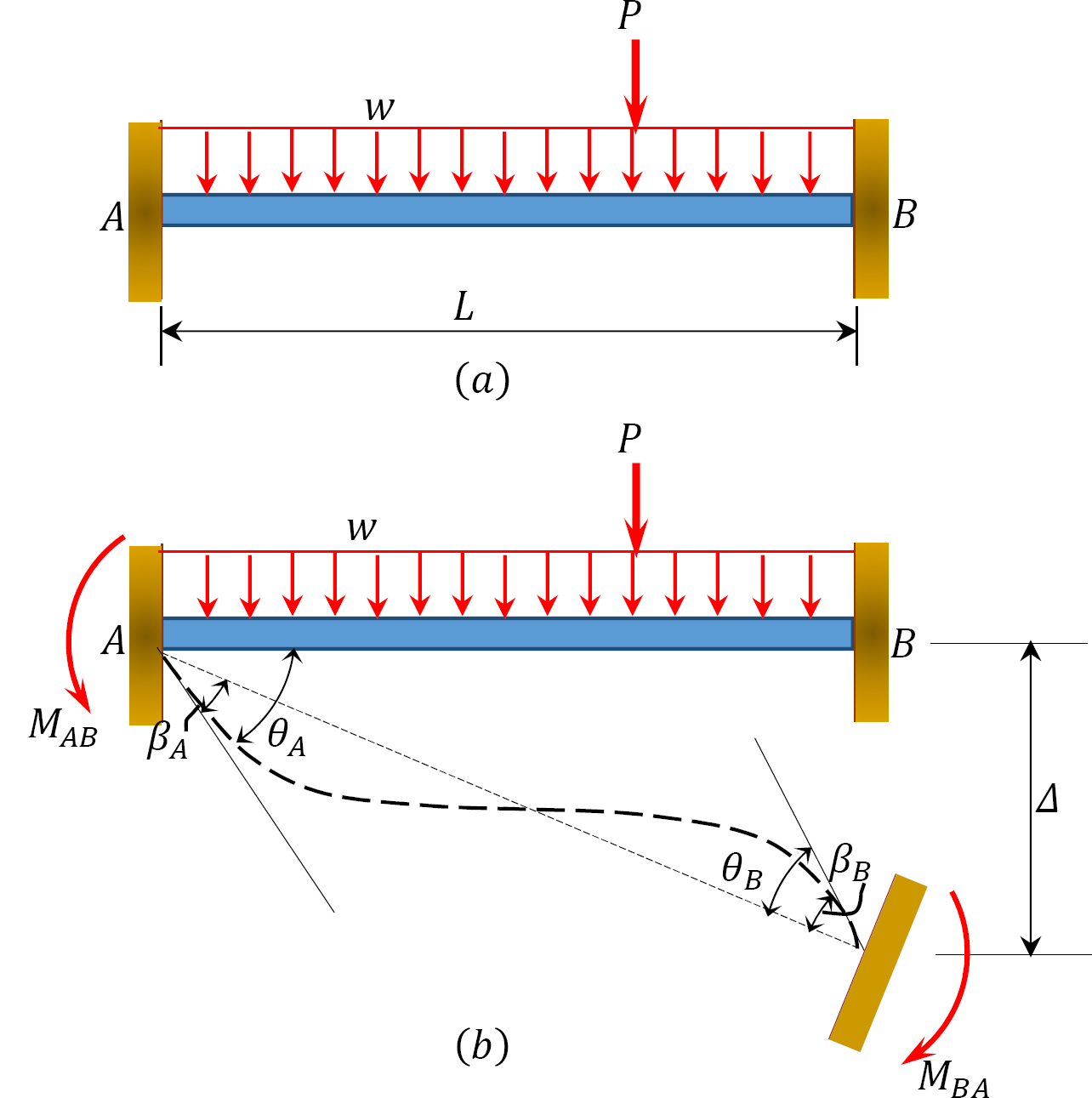
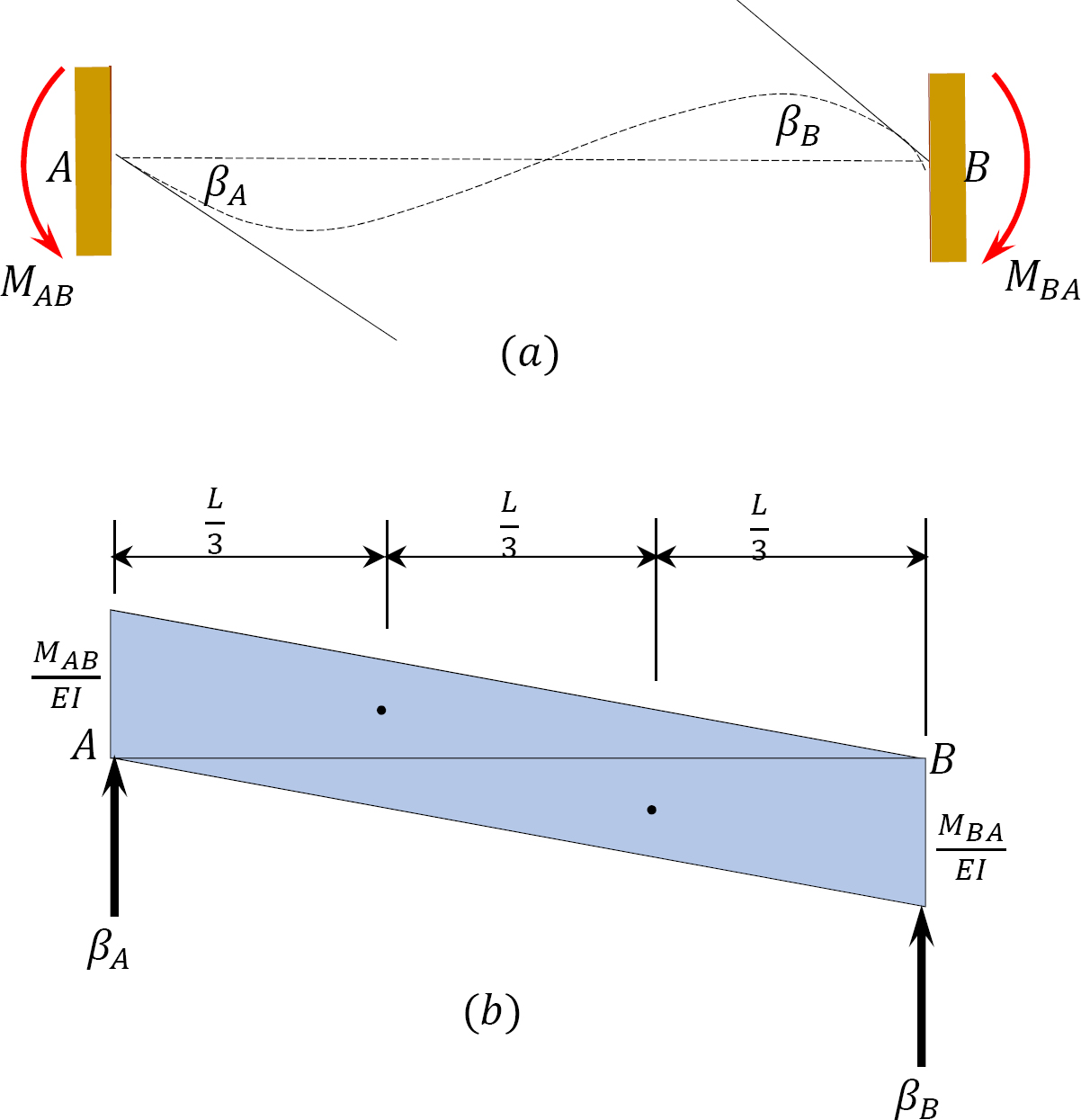
According to the moment-area theorem, the change in slope for a particular beam equals the end shear force of the beam when it is loaded with the 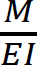 diagram. Thus, for the beam under consideration, the rotations βA and βB, shown in Figure 11.2, are obtained as follows:
diagram. Thus, for the beam under consideration, the rotations βA and βB, shown in Figure 11.2, are obtained as follows:
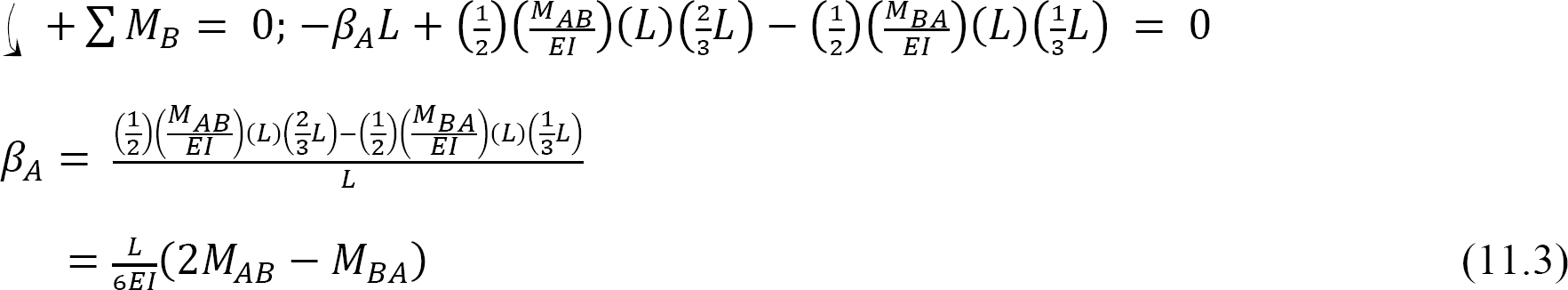
Similarly, taking the moment about end A to determine βB suggests the following:
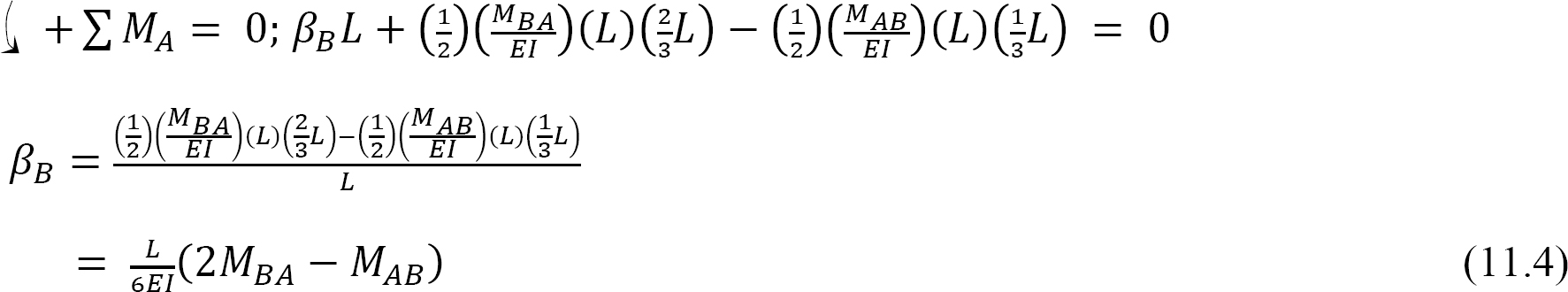
Solving equations 11.3 and 11.4 suggests the following:


Solving equations 11.1 and 11.2 for βA and βB and substituting them into equations 11.5 and 11.6 suggests the following:


Putting 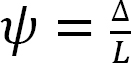 into equations 10.10 and 10.11 suggests the following:
into equations 10.10 and 10.11 suggests the following:


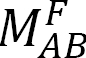 and
and 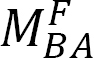 ).
).The final end moments can then be computed as the summation of the moments caused by slopes, deflections, and fixed-end moments, as follows:
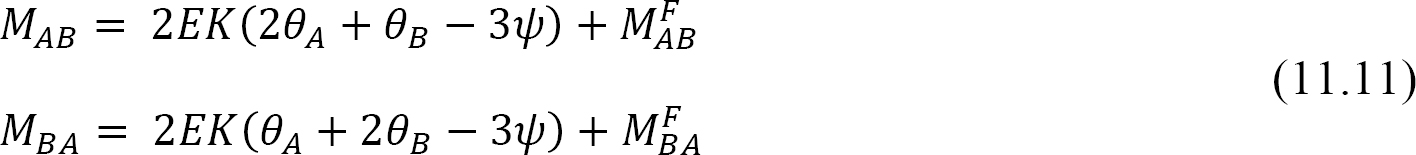
where
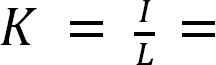 stiffness factor.
stiffness factor.
11.4 Modification for Pin-Supported End Span
The analysis of beams or frames supported by a pin or roller at the far end of the span is simplified by using the modified slope-deflection equation derived below. Using the modified equation reduces the amount of computational work, as the equation is applied only once to the span with a pin or roller at the far end.
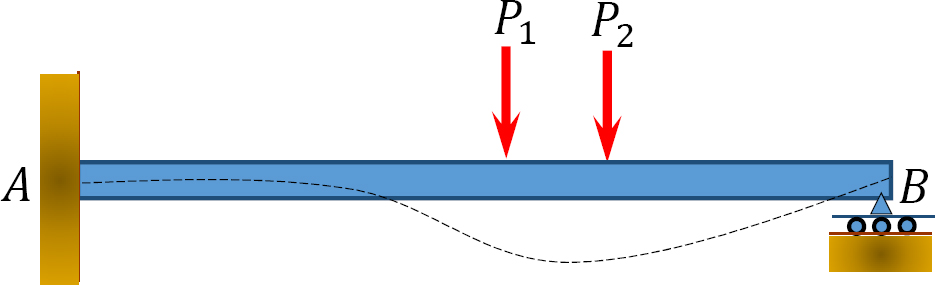
Consider the propped cantilever beam shown in Figure 11.5. The slope-deflection equations for the end moments are as follows:

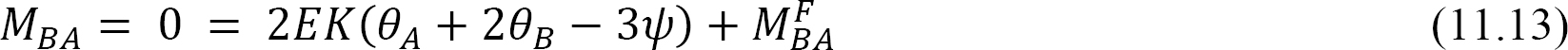
Solving equation 11.13 for θB and substituting it into equation 11.12 suggests the following:
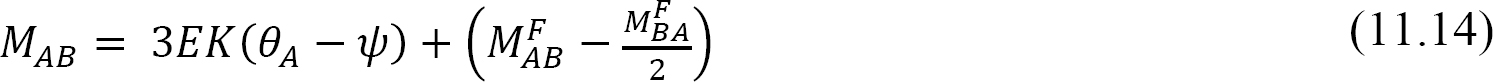
Equation 11.14 is the modified slope-deflection equation when the far end is supported by a pin or roller.
11.5 Analysis of Indeterminate Beams
The procedure for the analysis of indeterminate beams by the slope-deflection method is summarized below.
Procedure for Analysis of Indeterminate Beams and Non-Sway Frames by the Slope-Deflection Method
•Determine the fixed-end moments for the members of the beam.
•Determine the rotations of the chord if there is any support settlement.
•Write the slope-deflection equation for the members’ end moments in terms of unknown rotations.
•Write the equilibrium equations at each joint that is free to rotate in terms of the end moments of members connected at that joint.
•Solve the system of equations obtained simultaneously to determine the unknown joint rotations.
•Substitute the computed joint rotations into the equations obtained in step 3 to determine the members’ end moments.
•Draw a free-body diagram of the indeterminate beams indicating the end moments at the joint.
•Draw the shearing force diagrams of the beam by considering the freebody diagram of each span of the beam in the case of a multi-span structure.
11.6 Analysis of Indeterminate Frames
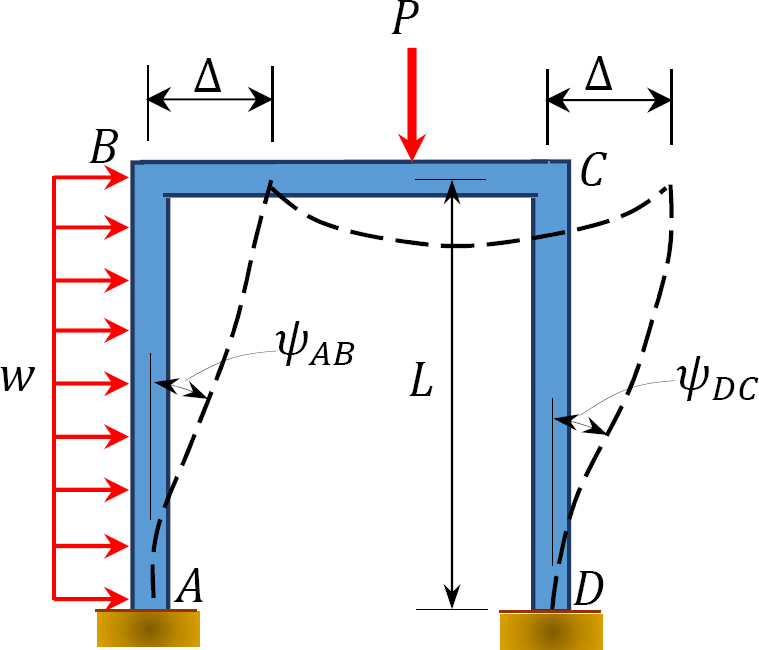
Indeterminate frames are categorized as frames with or without side-sway. A frame with side-sway is one that permits a lateral moment or a swaying to one side due to the asymmetrical nature of its structure or loading. The analysis of frames without side-sway is similar to the analysis of beams considered in the preceding section, while the analysis of frames with side-sway requires taking into consideration the effect of the lateral movement of the structure.
11.6.1 Analysis of Frames with Side-Sway
Consider the frame shown in Figure 11.6 for an illustration of the effect of side-sway on a frame. Due to the asymmetrical application of the loads, there will be a lateral displacement ∆ to the right at B and C, which subsequently will cause chord rotations 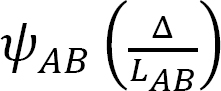 and
and 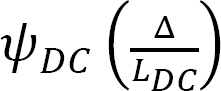 in columns AB and DC, respectively. These rotations must be considered when writing the slope-deflection equations for the columns, as will be demonstrated in the solved examples.
in columns AB and DC, respectively. These rotations must be considered when writing the slope-deflection equations for the columns, as will be demonstrated in the solved examples.
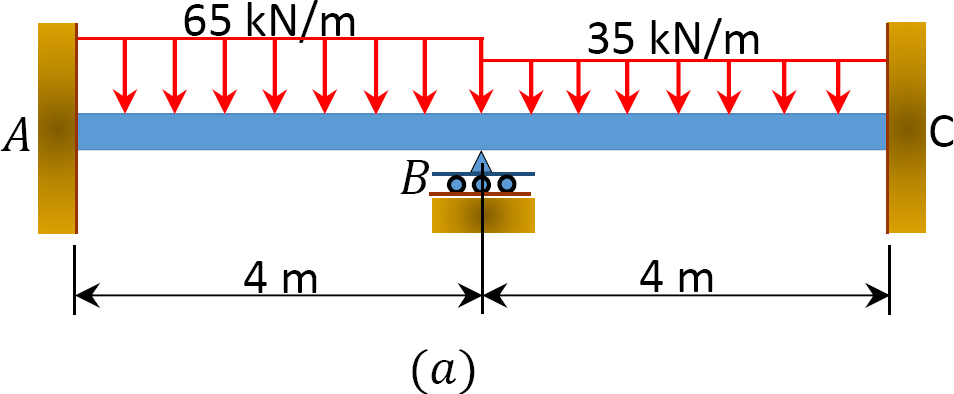
Example 11.1
Using the slope-deflection method, determine the end moments and the reactions at the supports of the beam shown in Figure 11.7a and draw the shearing force and the bending moment diagrams. EI = constant.
Solution
Fixed-end moments.
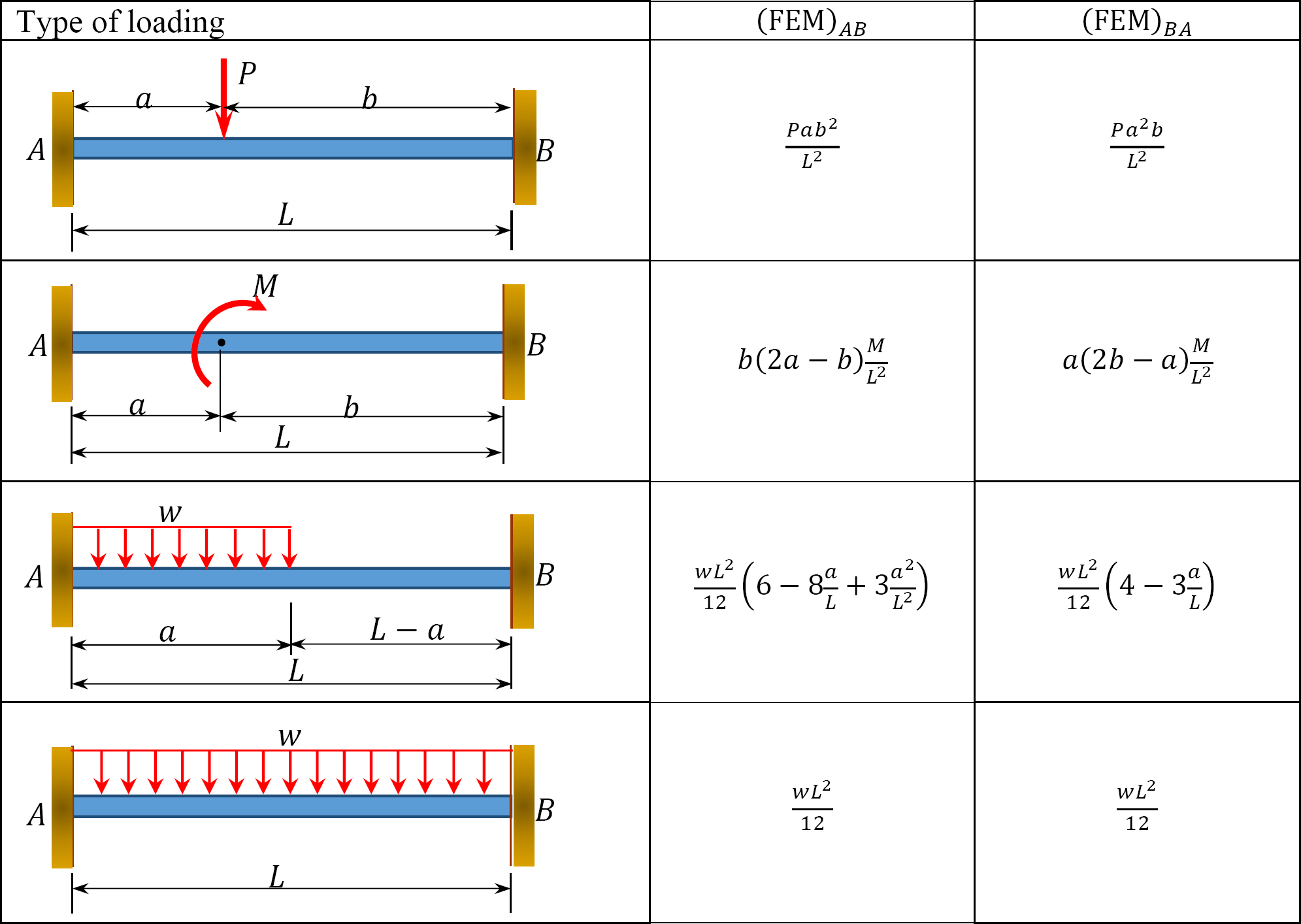
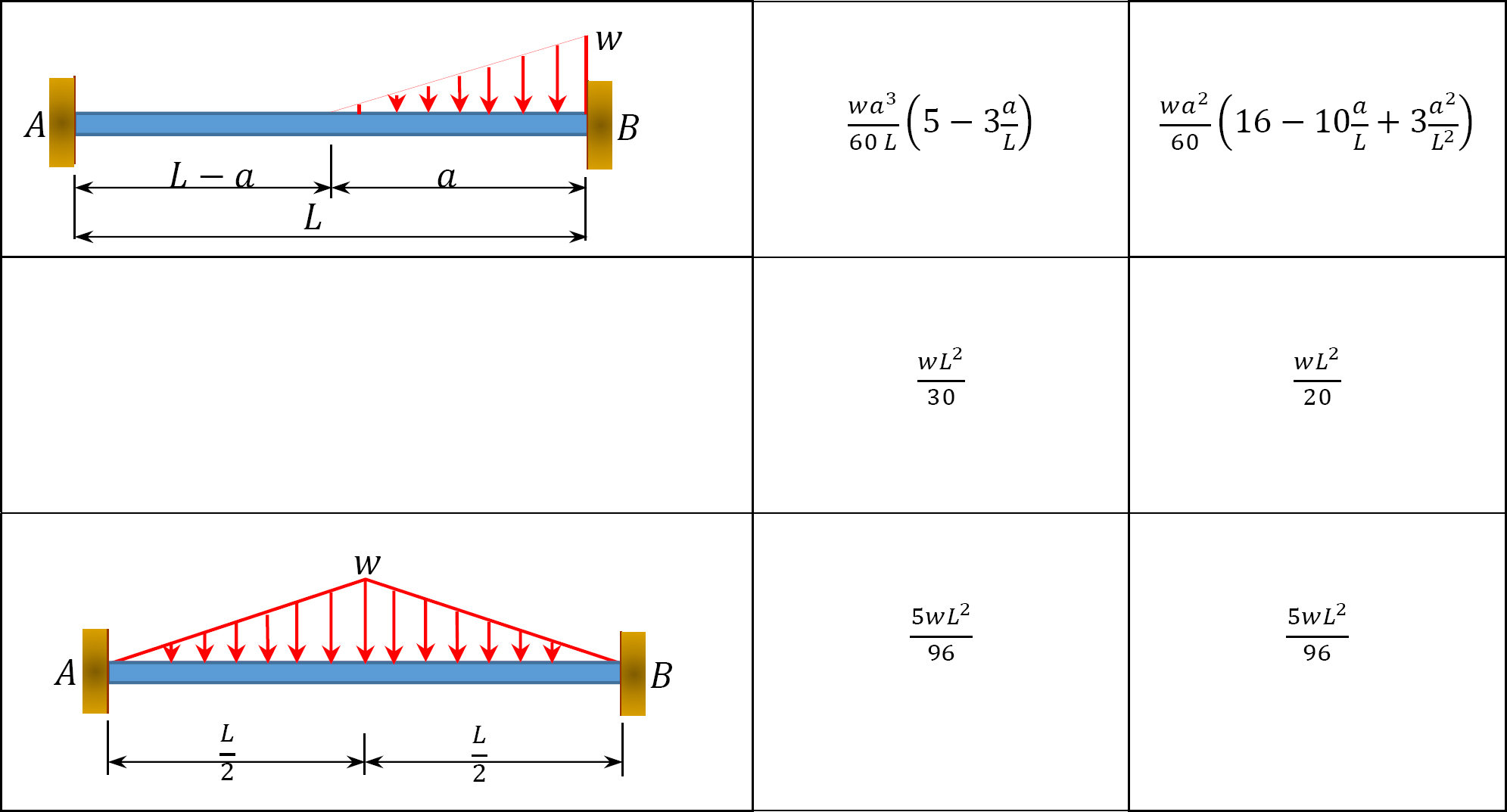
The Fixed-end moments (FEM) using Table 11.1 are computed as follows:
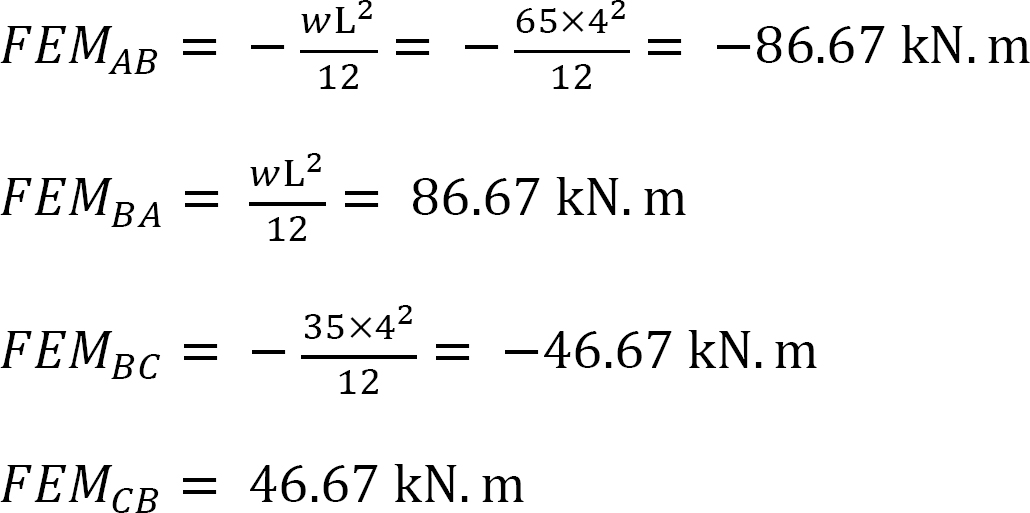
Slope-deflection equations. As θA = θC = 0 due to fixity at both ends and ψAB = ψBC = 0 as no settlement occurs, equations for member end moments are expressed as follows:

Joint equilibrium equation.
Equilibrium equation at joint B is as follows:
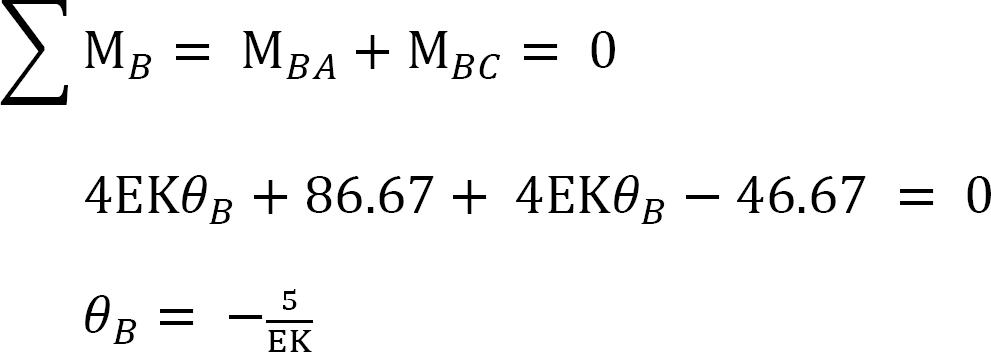
Final end moments.
Substituting 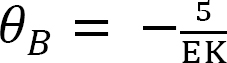 into equations 1, 2, 3, and 4 suggests the following:
into equations 1, 2, 3, and 4 suggests the following:
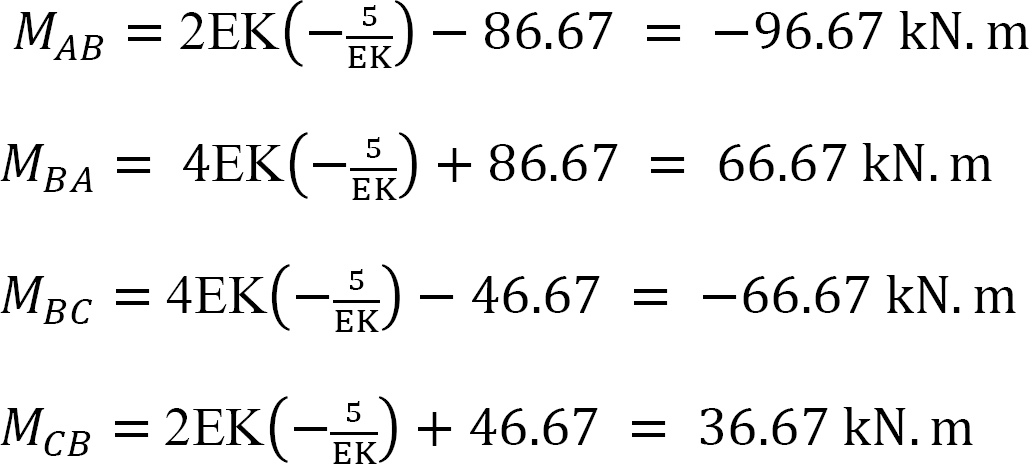
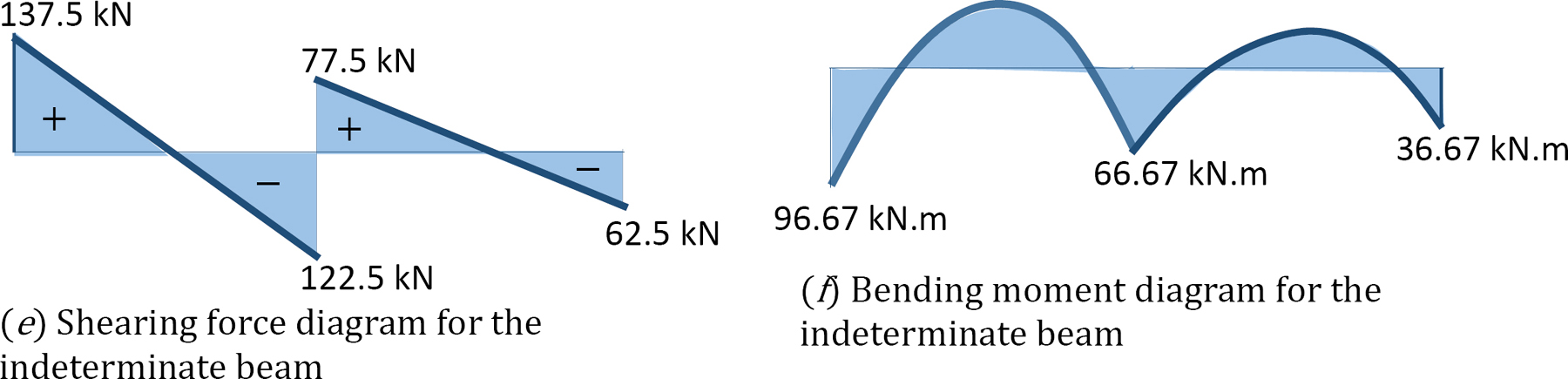
Shearing force and bending moment diagrams.
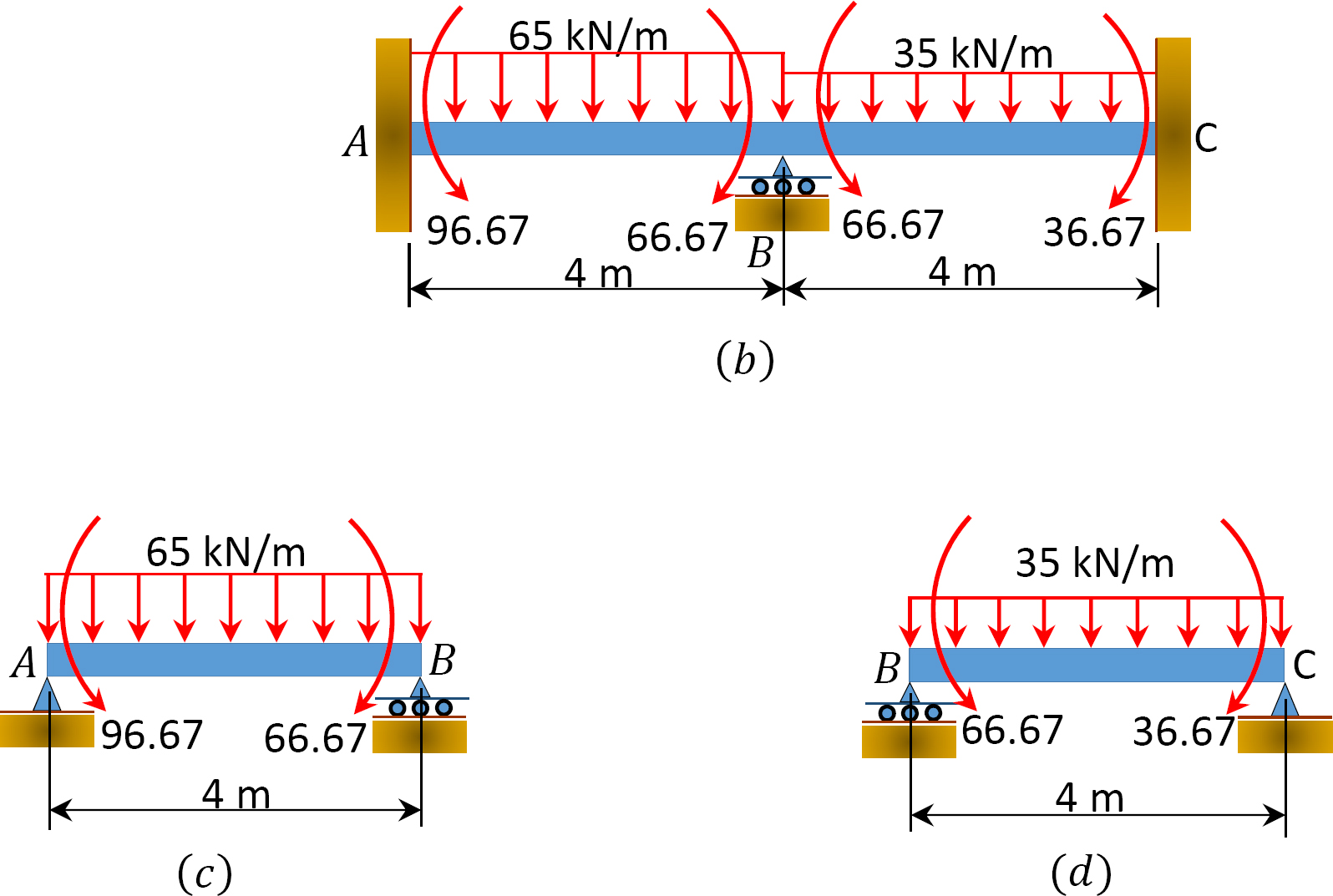
Shear force and bending moment for segment AB.
First compute the reaction at support A, as follows:
↶ + ∑ MB = 0: –4Ay + 96.67 + (65)(4)(2) – 66.67 = 0
Ay = 137.5 kN
Calculate the shear force, as follows:
V = 137.5 – 65x
When x = 0, V = 137.5 kN
When x = 4 m, V = –122.5 kN
Find the moment, as follows:
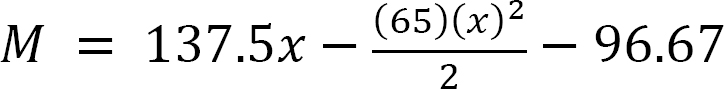
When x = 0, M = –96.67 kN. m
When x = 4 m, M = –66.67 kN. m
Shear force and bending moment for segment AB.
First determine the reaction at B, as follows:
↶ + ∑ MC = 0: –4By + 66.67 + (35)(4)(2) – 36.67 = 0
By = 77.5 kN
Calculate the shear force, as follows:
V = 77.5 – 35x
When x = 0, V = 77.5 kN.
When x = 4 m, V = –62.5 kN.
Find the moment, as follows:
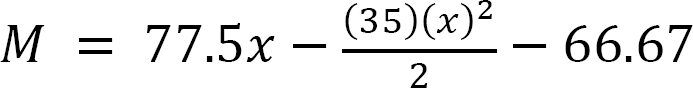
When x = 0, M = –66.67 kN. m
When x = 4 m, M = –36.67 kN. m
Shear force and bending moment diagrams.
Example 11.2
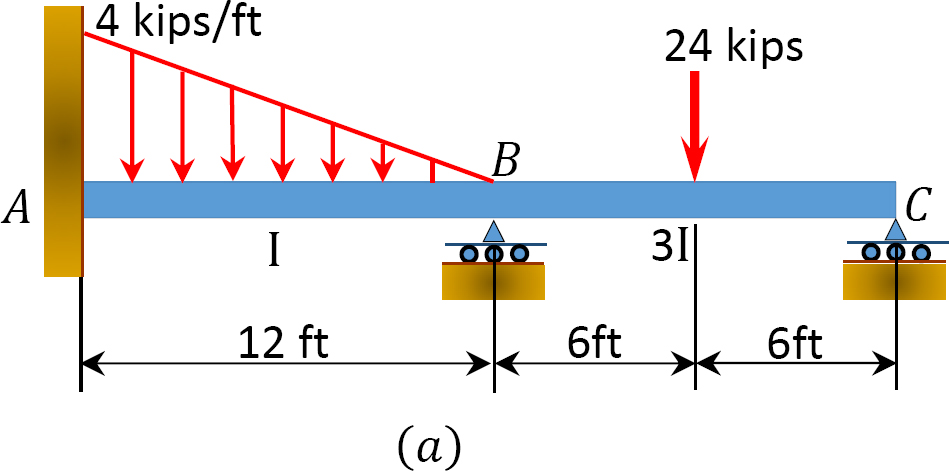
Using the slope-deflection method, determine the end moments and the reactions at the supports of the beam shown in Figure 11.8a, and draw the shearing force and the bending moment diagrams. EI = constant.
Solution
Relative stiffness.
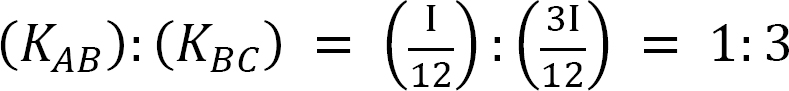
Fixed-end moments.
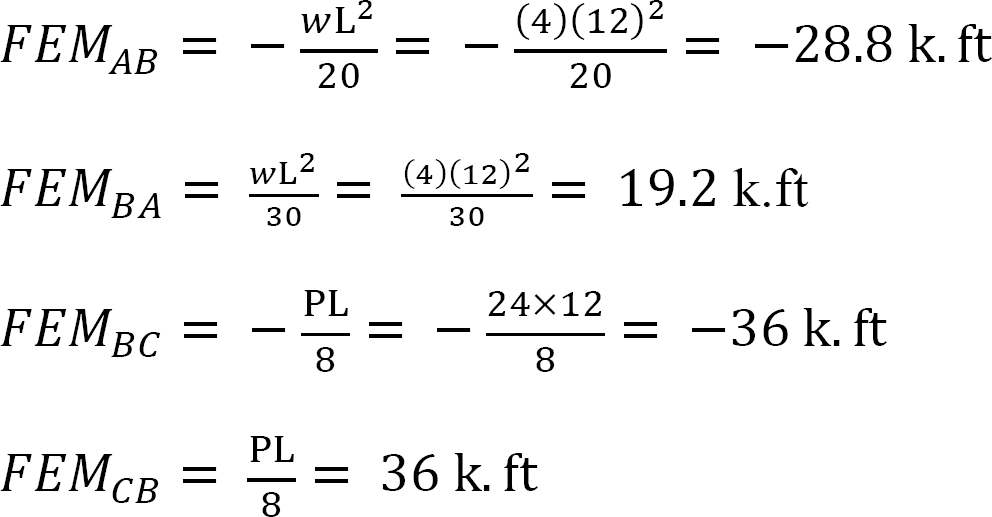
Slope-deflection equations.
Noting that MCB = Ψ = 0, equations for member end moments can be expressed as follows:
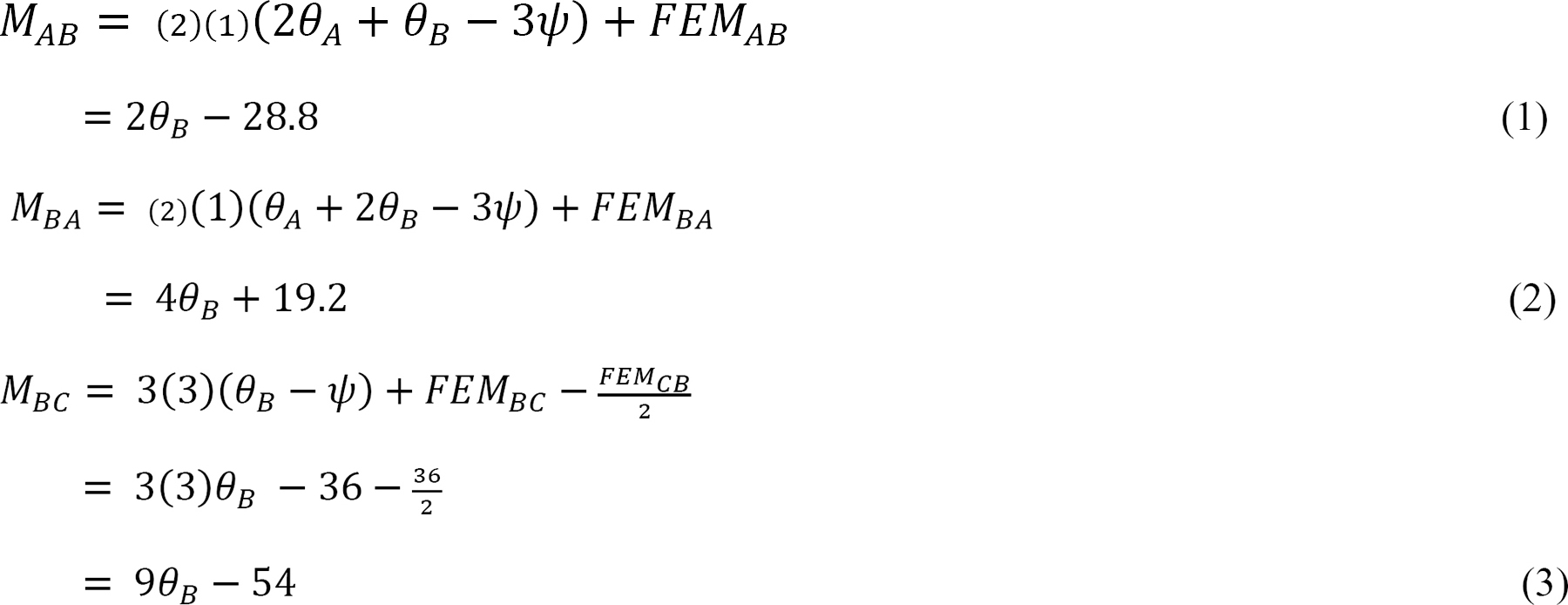
Joint equilibrium equation.
The equilibrium equation at joint B is as follows:
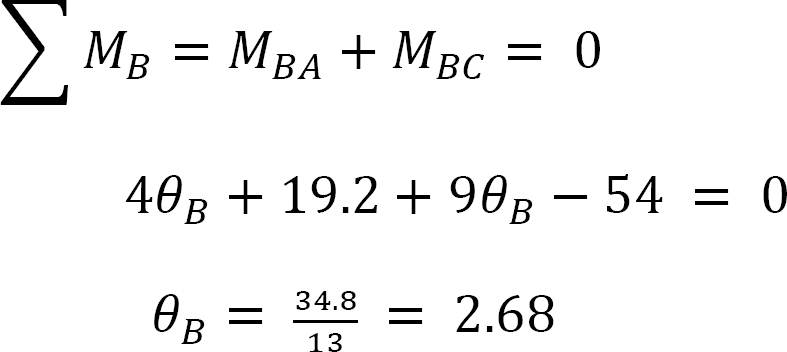
Final end moments.
Substituting the computed value of θB into equations 1, 2, and 3 suggests the following:
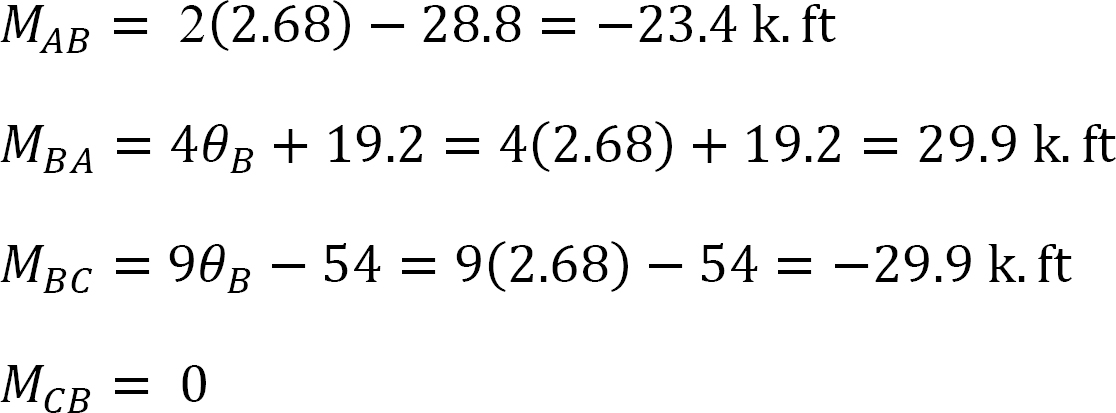
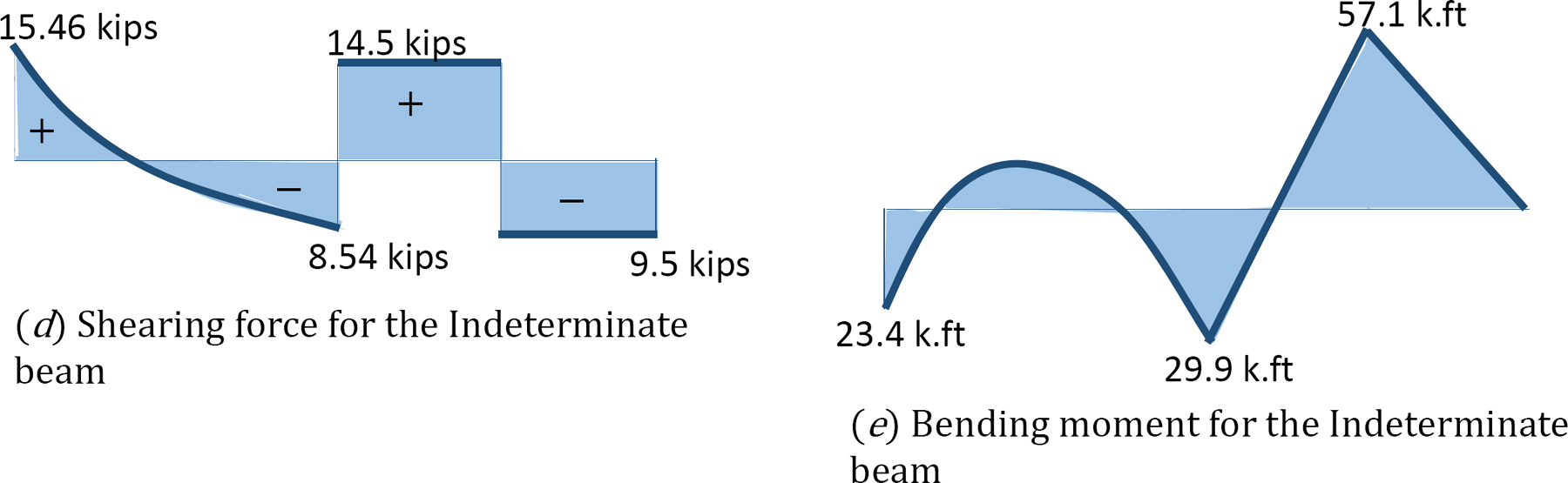
Shear force and bending moment diagrams.
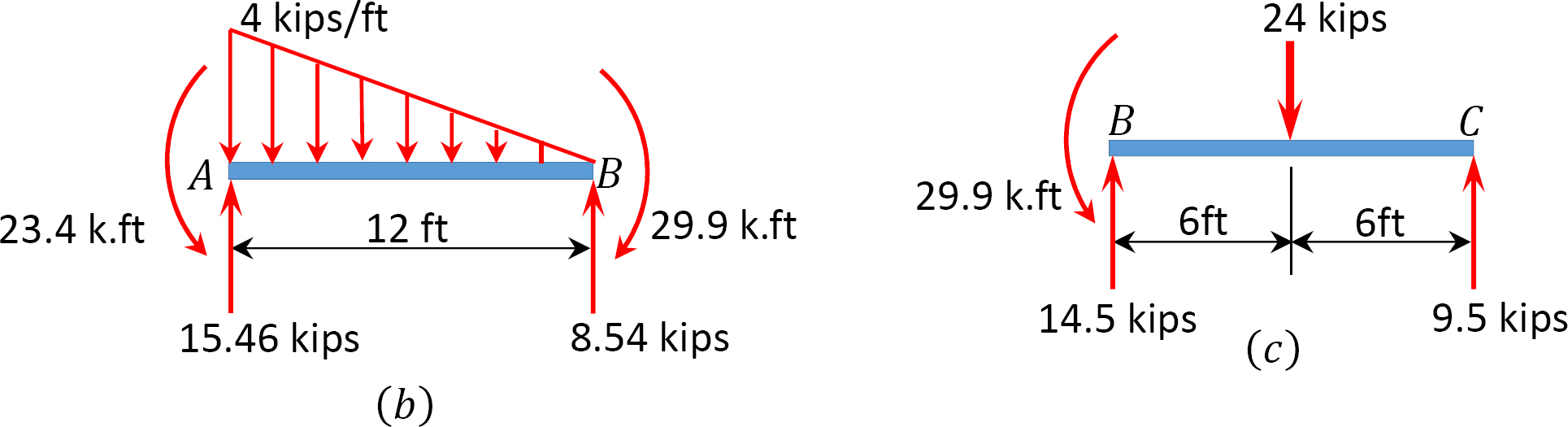
Shear force and bending moment for segment AB.
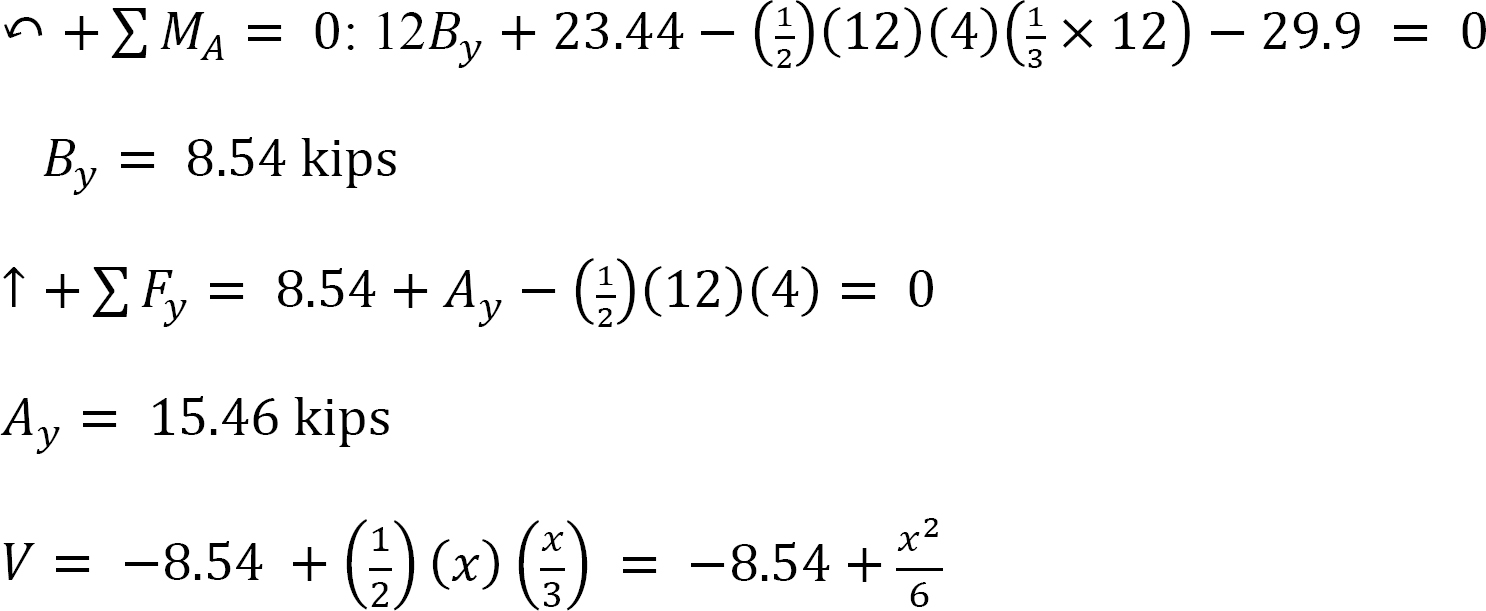
When x = 0, V = –8.54 kips
When x = 12 ft, V = 15.46 kips
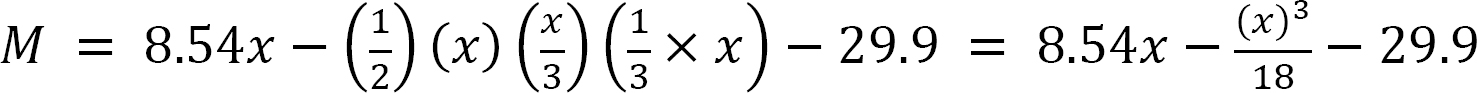
When x = 0, M = –29.9 k. ft
When x = 12ft, M = –23.4 k. ft
Shear force and bending moment for segment BC.
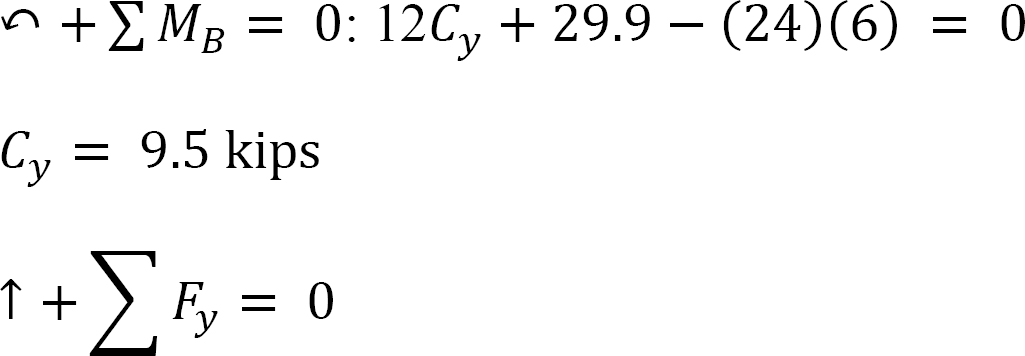
By + 9.5 – 24 = 0
By = 14.5 kips
0 < x < 6 ft
V = 14.5 kips
M = 14.5x – 29.9
When x = 0, M = –29.9 k. ft
When x = 6 ft, M = 57.10 k. ft
Example 11.3
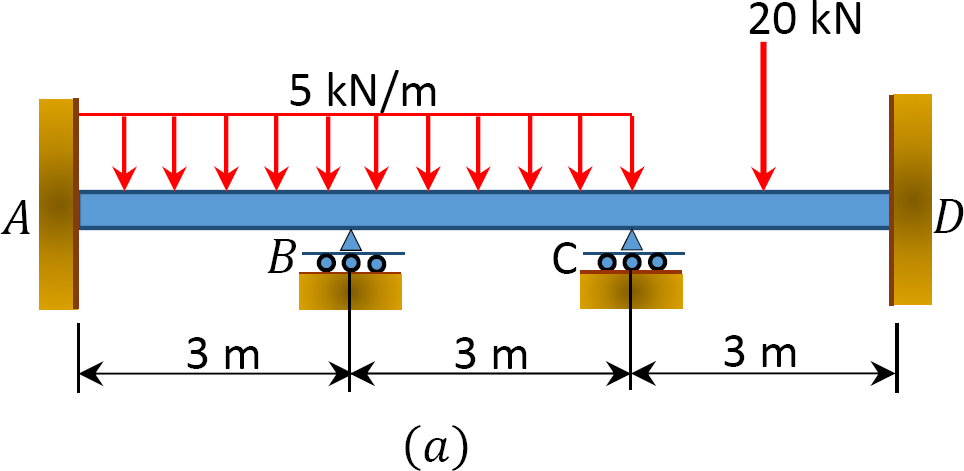
Using the slope-deflection method, determine the end moments of the beam shown in Figure 11.9a. Assume support B settles 1.5 in, and draw the shear force and the bending moment diagrams. The modulus of elasticity and the moment of inertia of the beam are 29,000 ksi and 8000 in4, respectively.
Solution
Fixed-end moments.
The Fixed-end moments (FEM) using Table 11.1 are computed as follows:
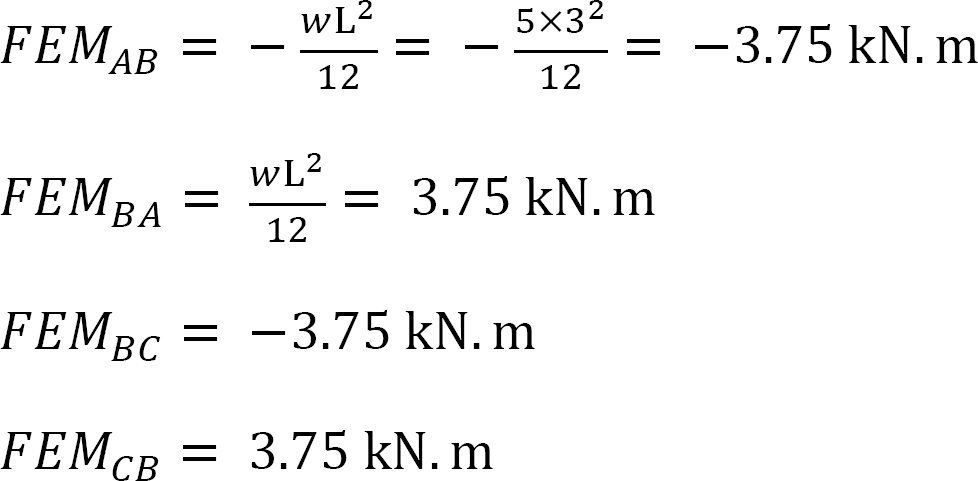
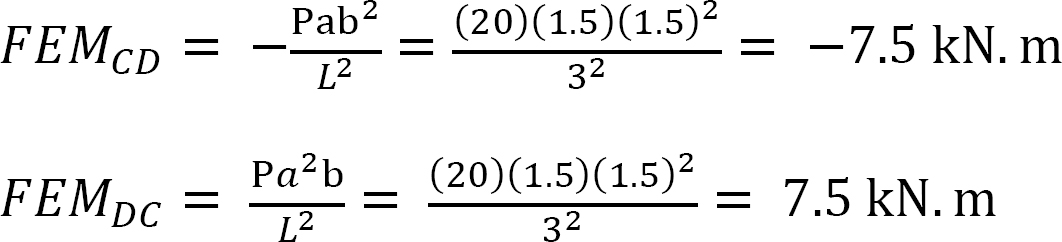
Slope-deflection equations.
At θA = θD = ψ = 0, the equations for member end moments are expressed as follows:
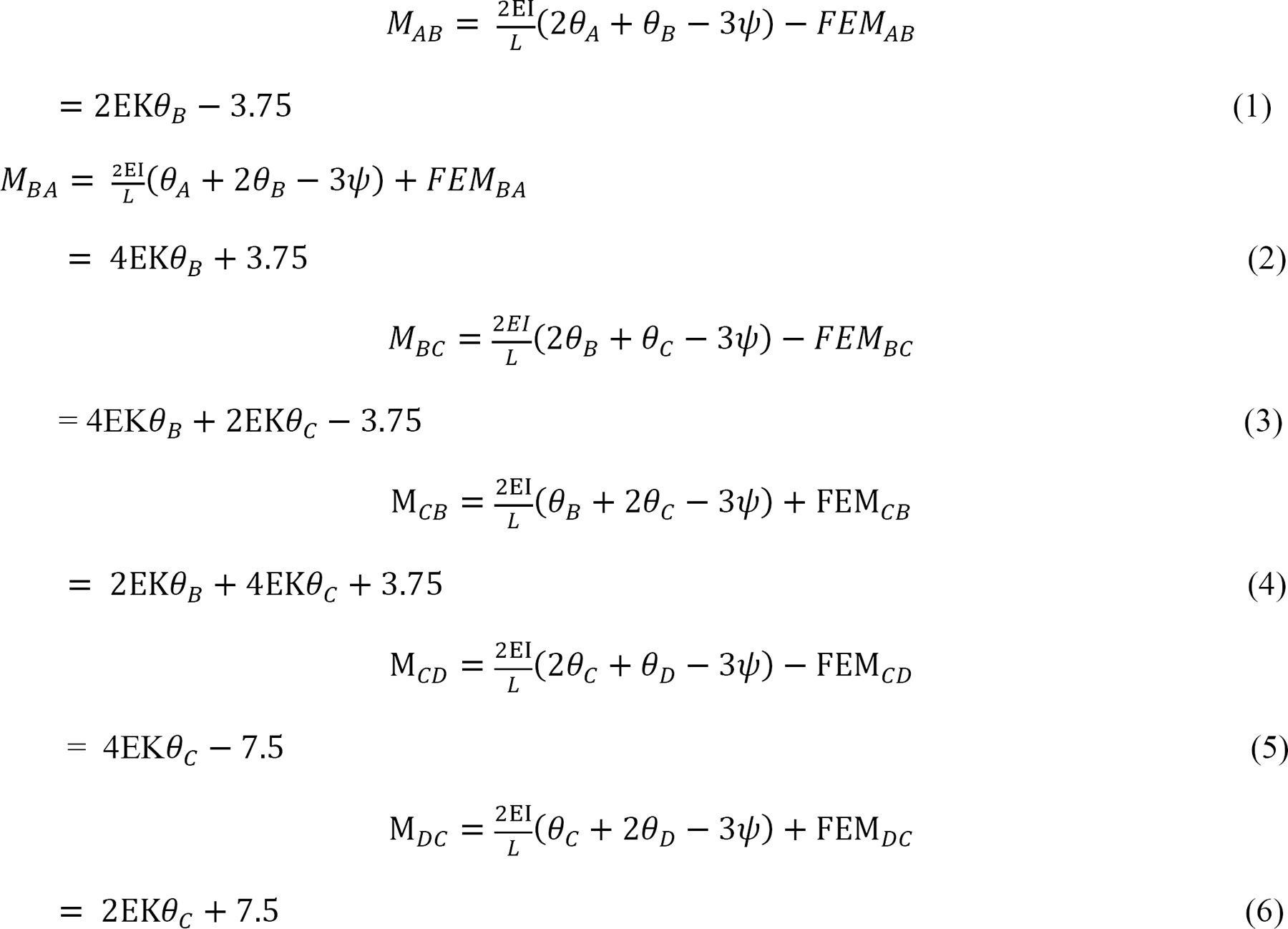
Joint equilibrium equation.
The equilibrium equation at joint B is as follows:
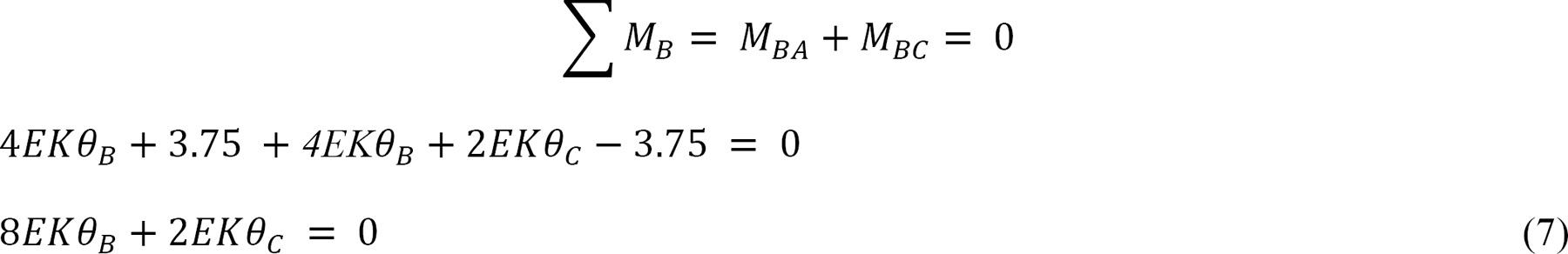
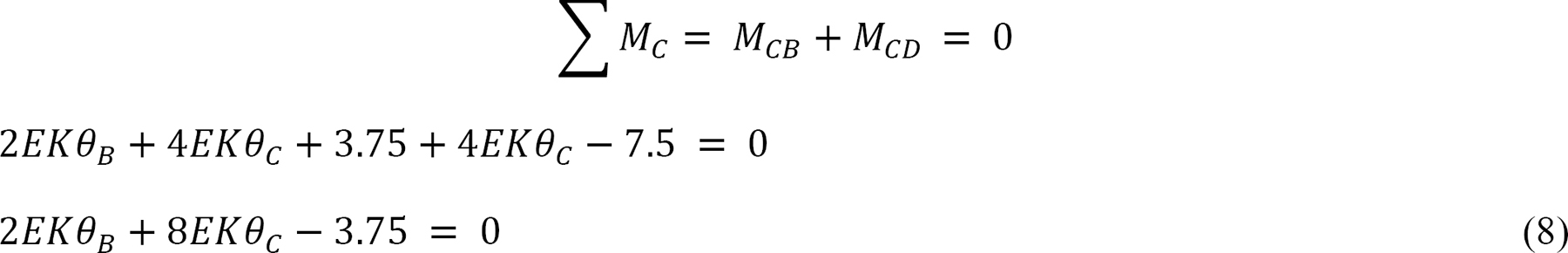
Solving equations 7 and 8 simultaneously suggests the following:
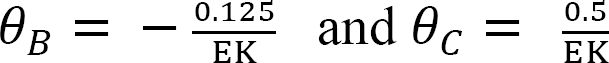
Final end moments.
Substituting the obtained values of θB and θC into the slope-deflection equations suggests the following end moments:

Example 11.4
Using the slope-deflection method, determine the member end moments of the beam of the rectangular cross section shown in Figure 11.10a. Assume that support B settles 2 cm. The modulus of elasticity and the moment of inertia of the beam are E = 210,000 N/mm2 and 4.8 × 104 mm,4 respectively.
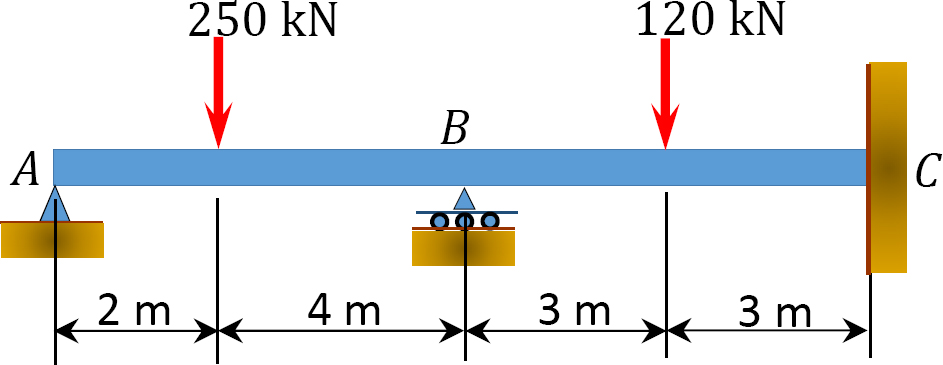
Solution
The Fixed-end moments (FEM) using Table 11.1 are computed as follows:
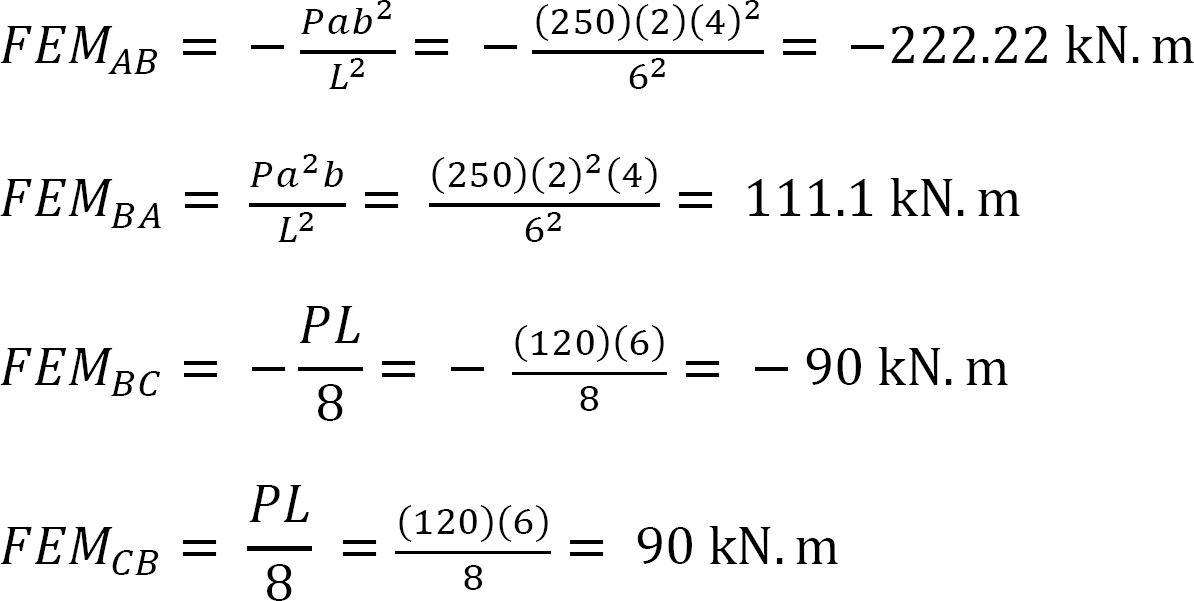
Slope-deflection equations.
As θC = 0, equations for member end moments are expressed as follows:
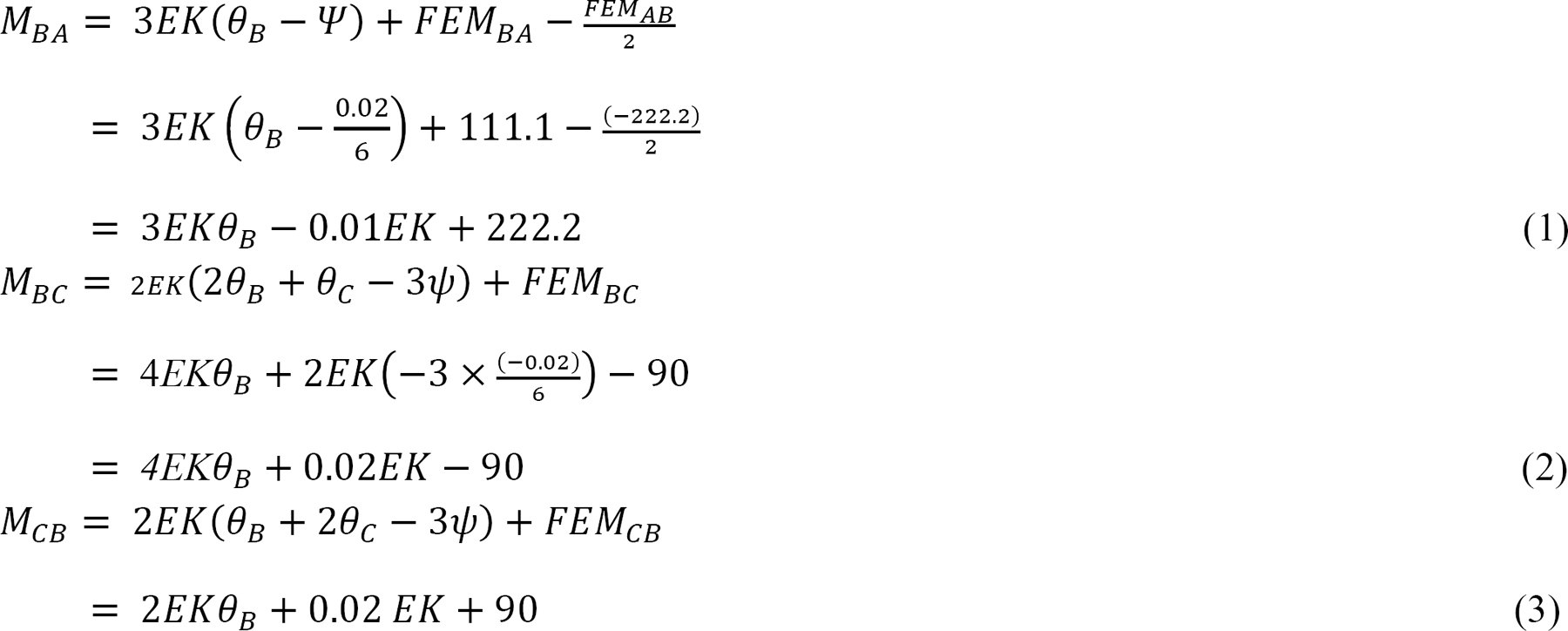
Joint equilibrium equation.
The equilibrium equation at joint B is written as follows:
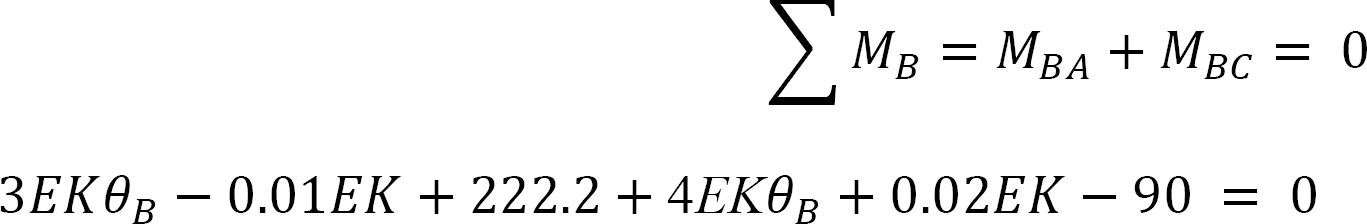

Solving equation 4 for θB suggests the following:
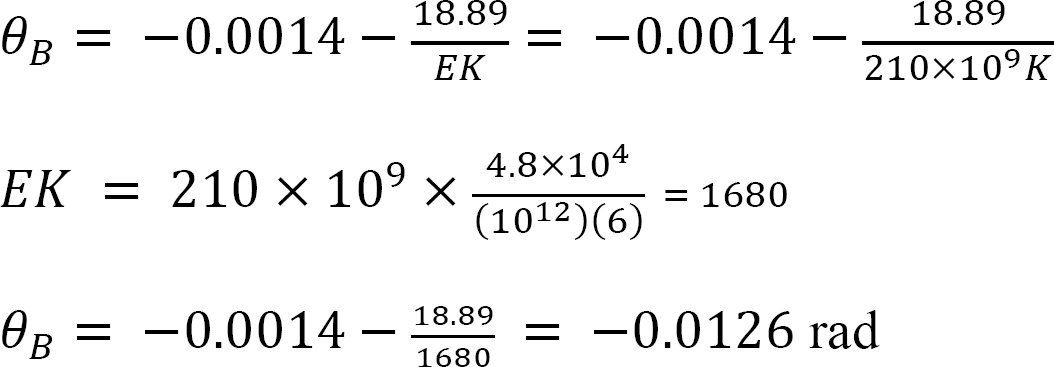
Final end moments.
Substituting the obtained value of θB into equations 1, 2, and 3 suggests the following end moments:
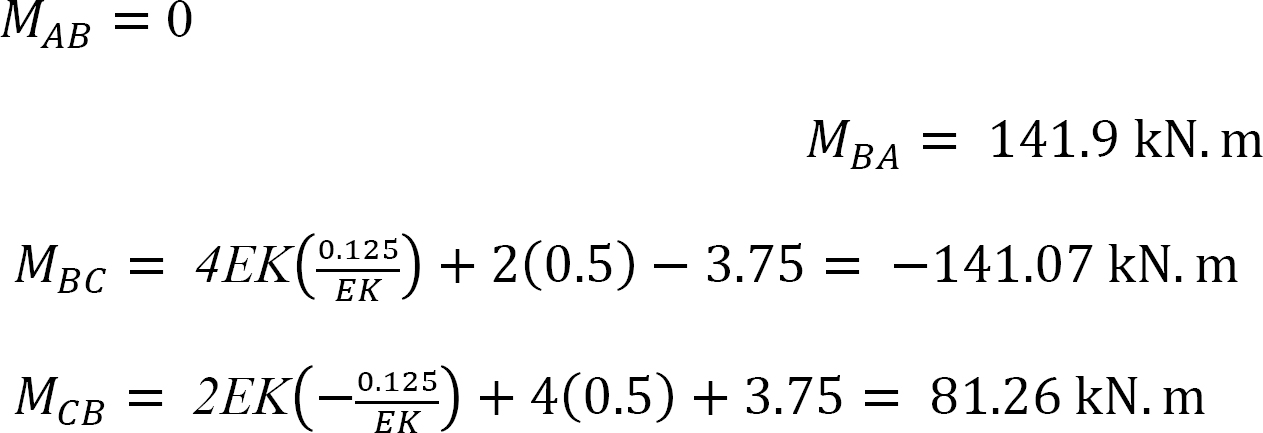
Example 11.5
Using the slope-deflection method, determine the member end moments and the reactions at the supports of the frame shown in Figure 11.11a. EI = constant.
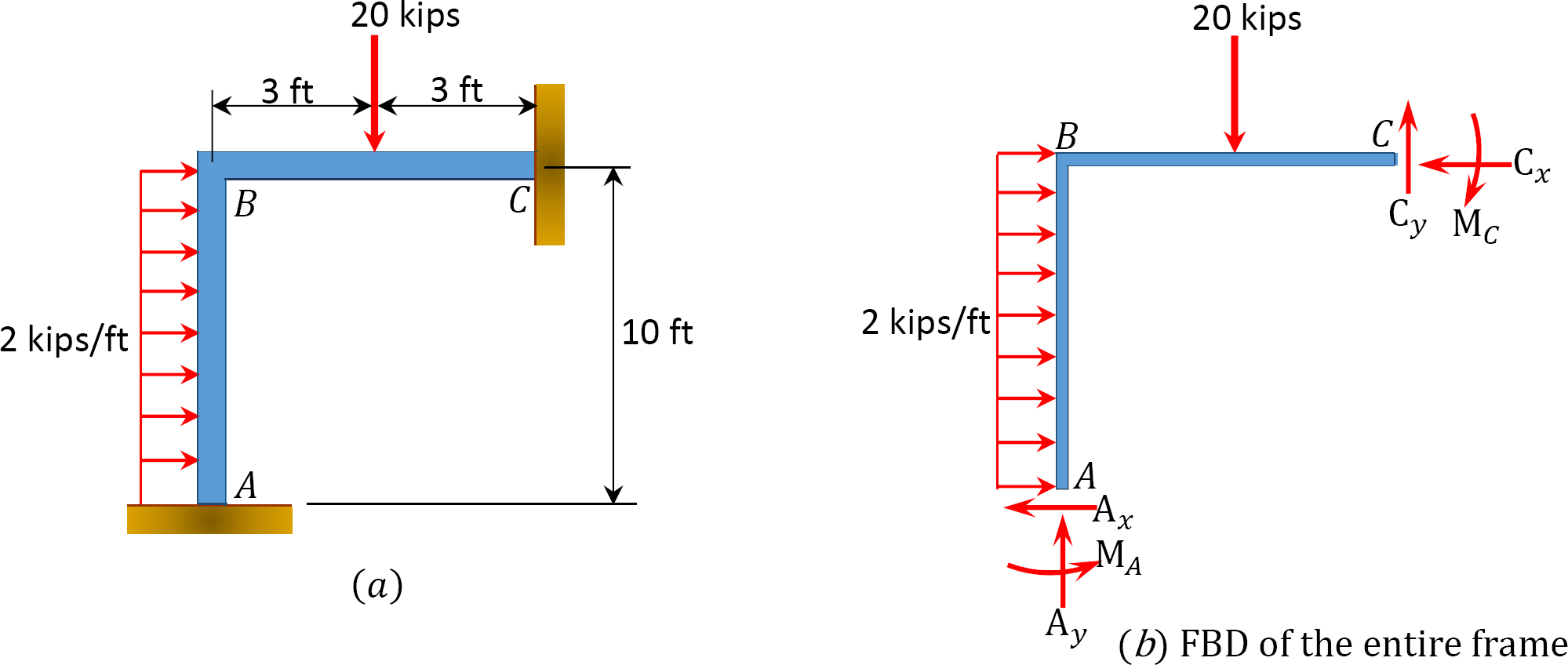
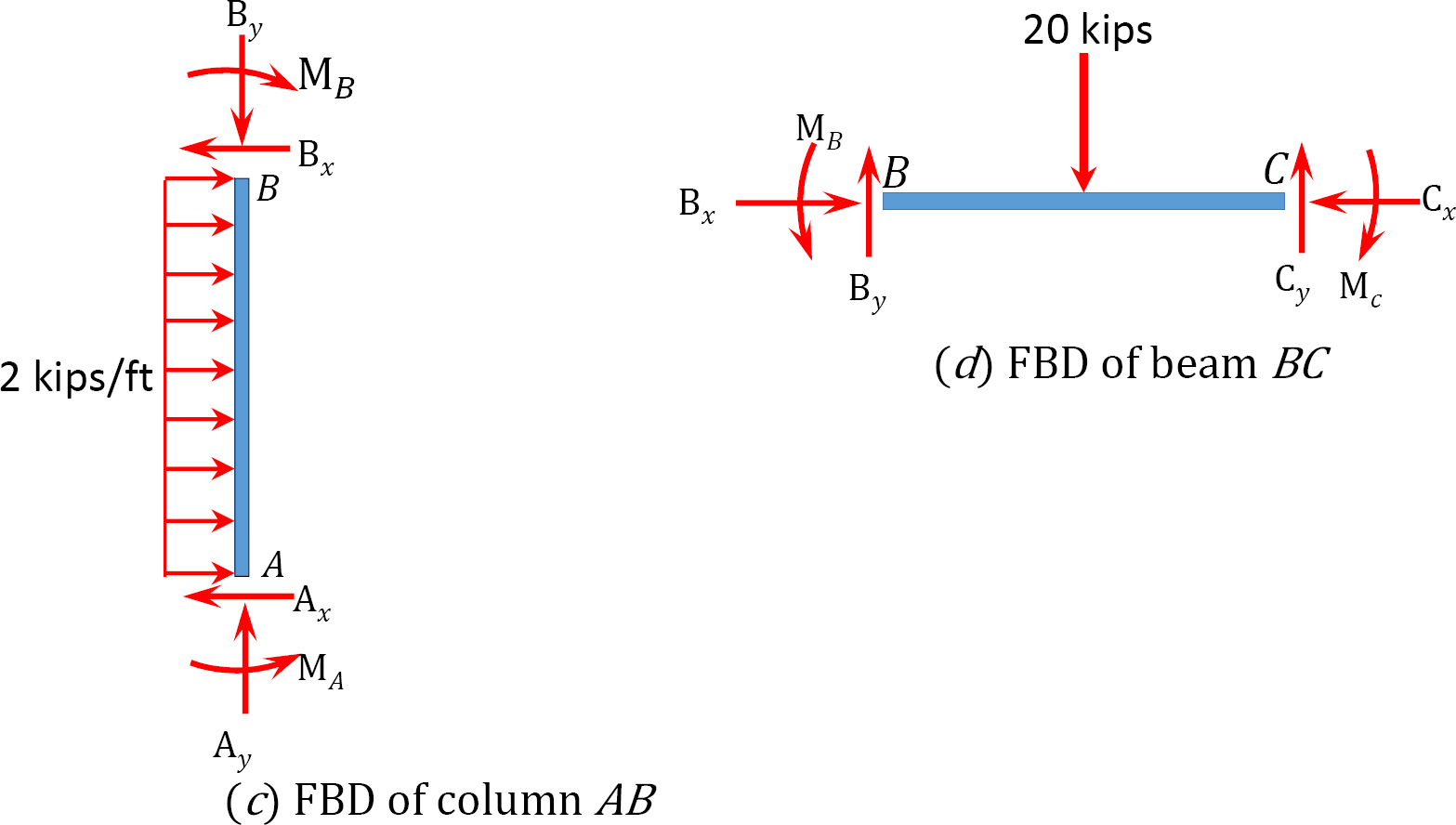
Solution
Fixed-end moments.
The Fixed-end moments (FEM) using Table 11.1 are computed as follows:
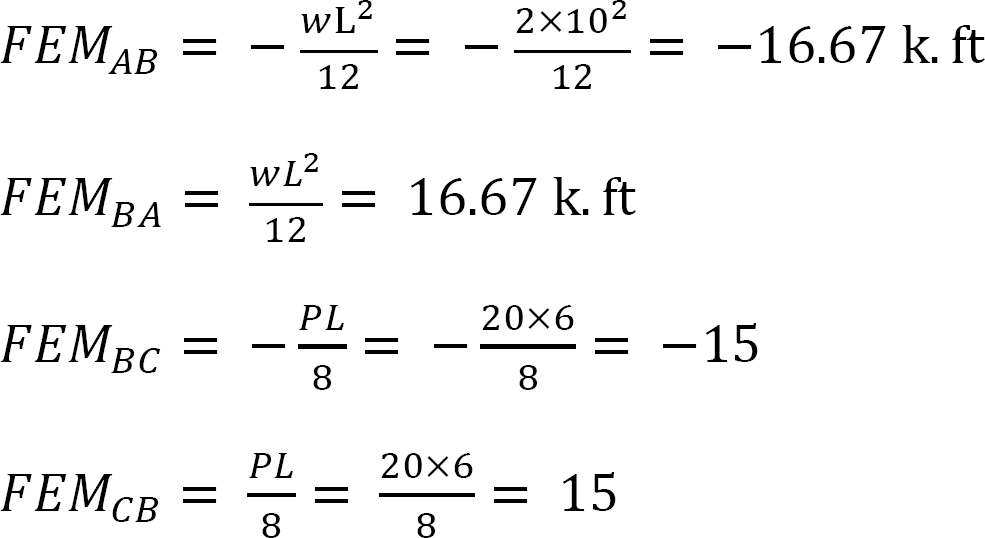
Slope-deflection equations.
As θA = θC = 0 due to fixity at both ends and ψAB = ψBC = 0 since no settlement occurs, equations for the member end moments are expressed as follows:
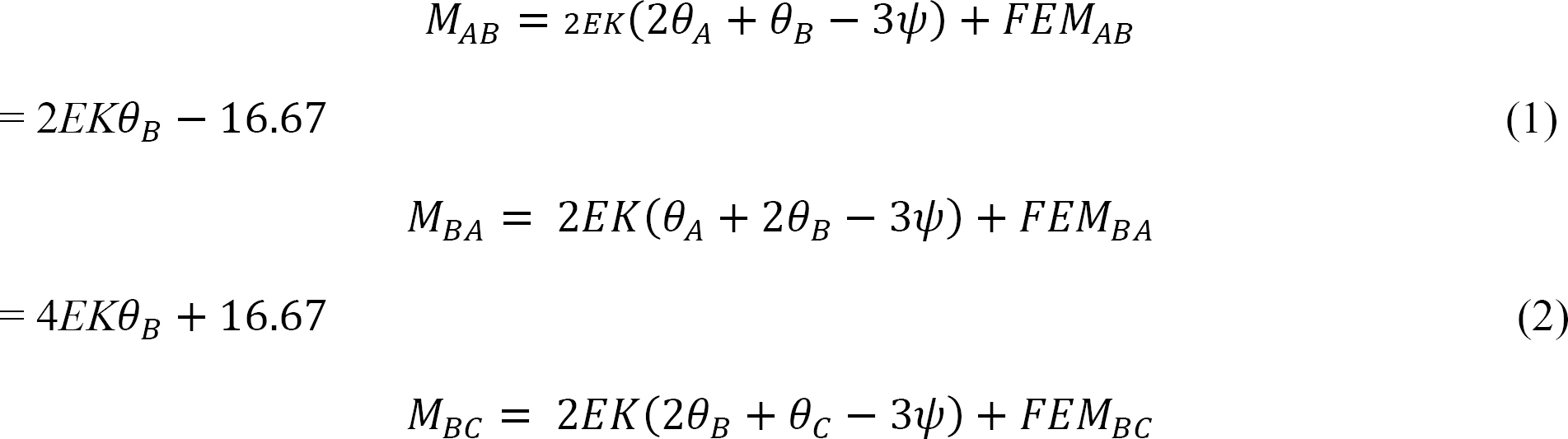
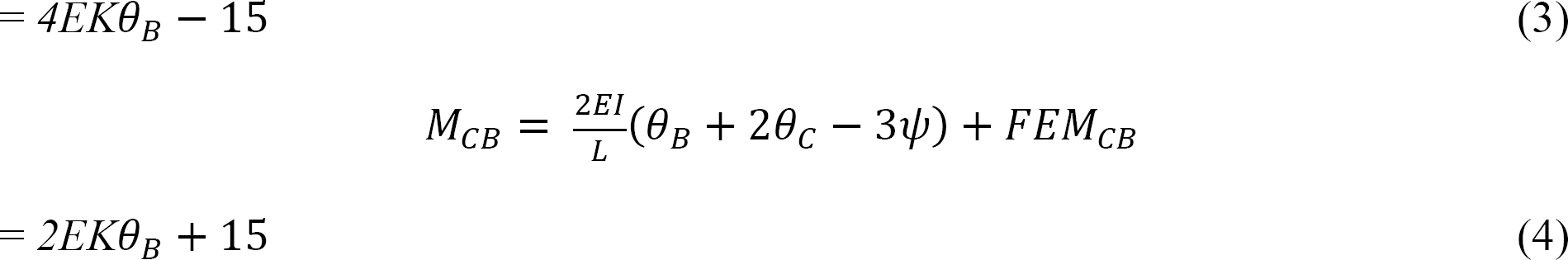
Joint equilibrium equation.
The equilibrium equation at joint B is as follows:
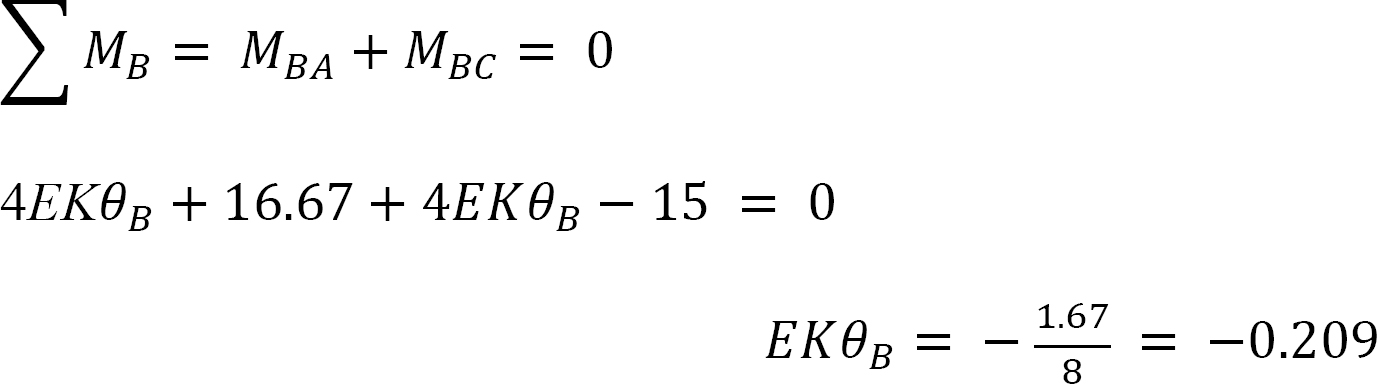
Final end moments.
Substituting EKθB = –0.209 into equations 1, 2, 3, and 4 suggests the following:
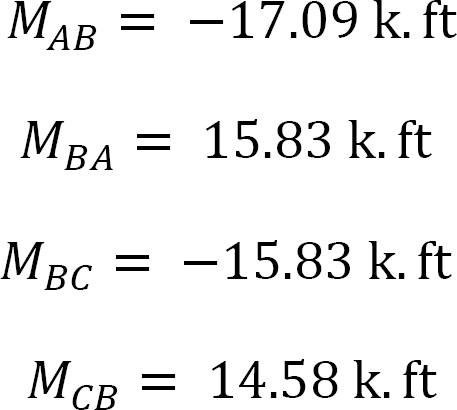
Reactions at supports.
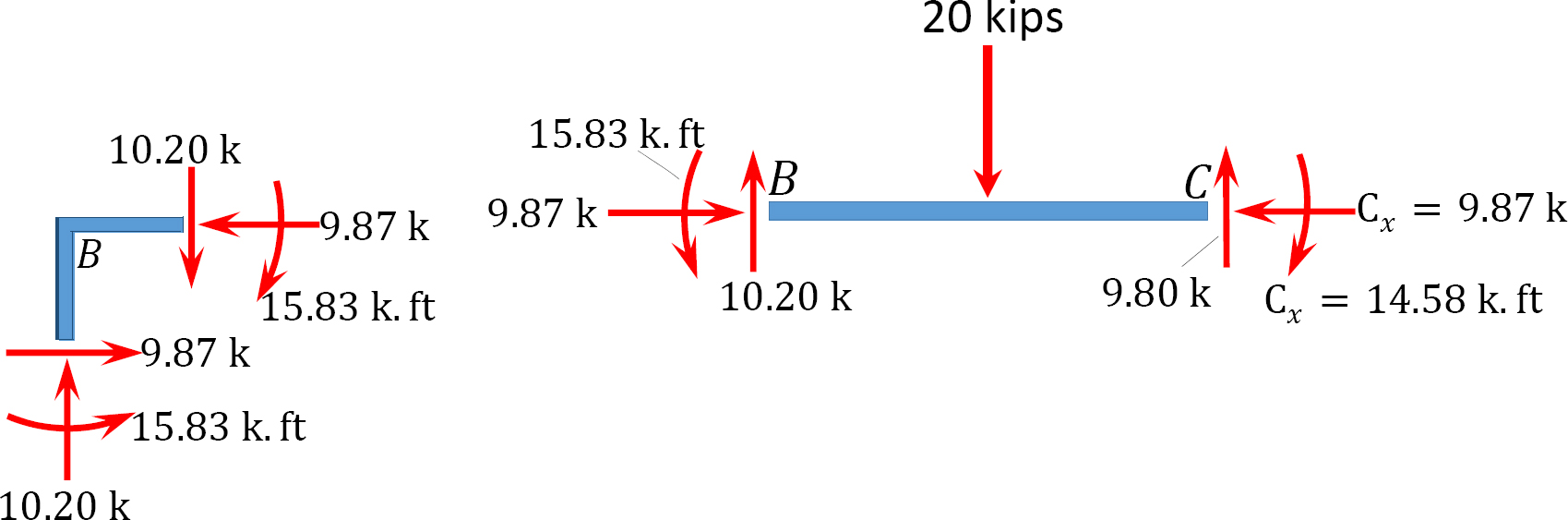
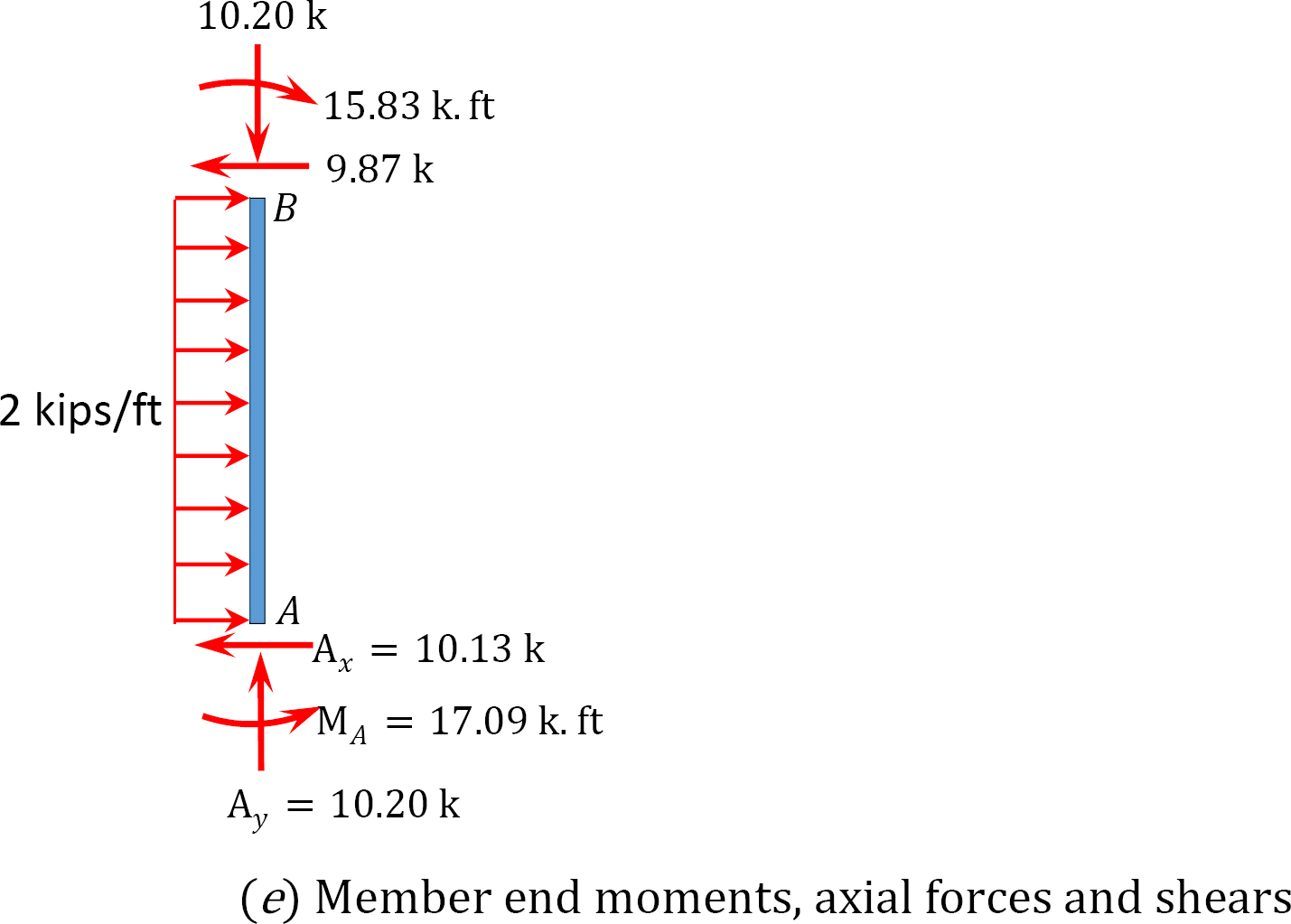
+ ↶ ∑ MB = 0: 17.09 + (2)(10)(5) – 15.83 – 10Ax = 0
Ax = 10.13 k
To determine Ay, take the moment about C in Figure 11.11b, as follows:
+ ↶ ∑ MC = 0; 17.09 – 10.13 × 10 + (2)(10)(5) + 20 × 3 – 14.58 – 6Ay = 0
Ay = 10.20 k
To determine Cy in Figure 11.11b, consider the summation of forces in the vertical direction, as follows:
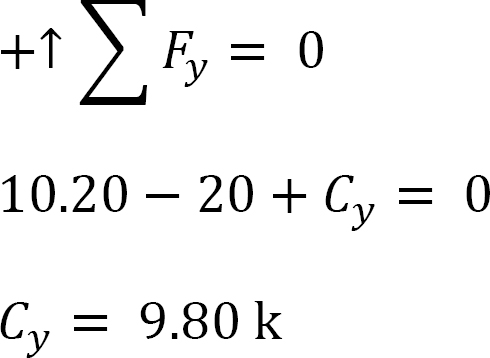
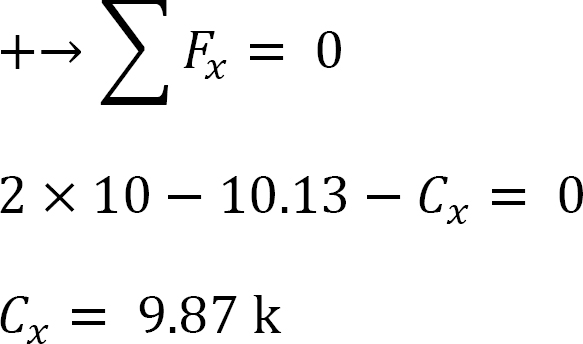
Example 11.6
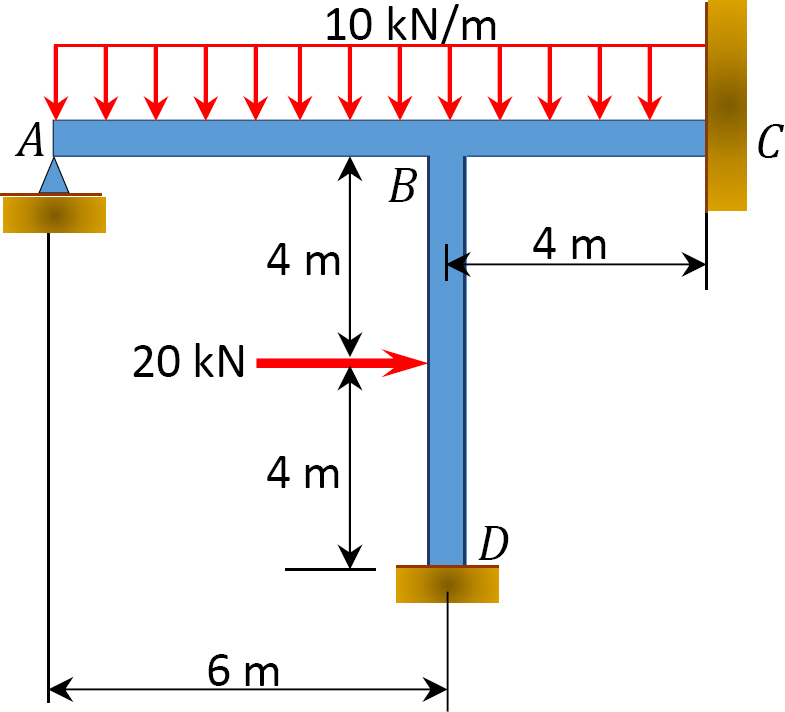
Using the slope-deflection method, determine the member end moments of the frame shown in Figure 11.12a.
Solution
Fixed-end moments.
The Fixed-end moments (FEM) using Table 11.1 are computed as follows:

Slope-deflection equations.
As θA = θC = 0 due to fixity at both ends and ψAB = ψBC = 0 since no settlement occurs, the equations for member end moments can be expressed as follows:
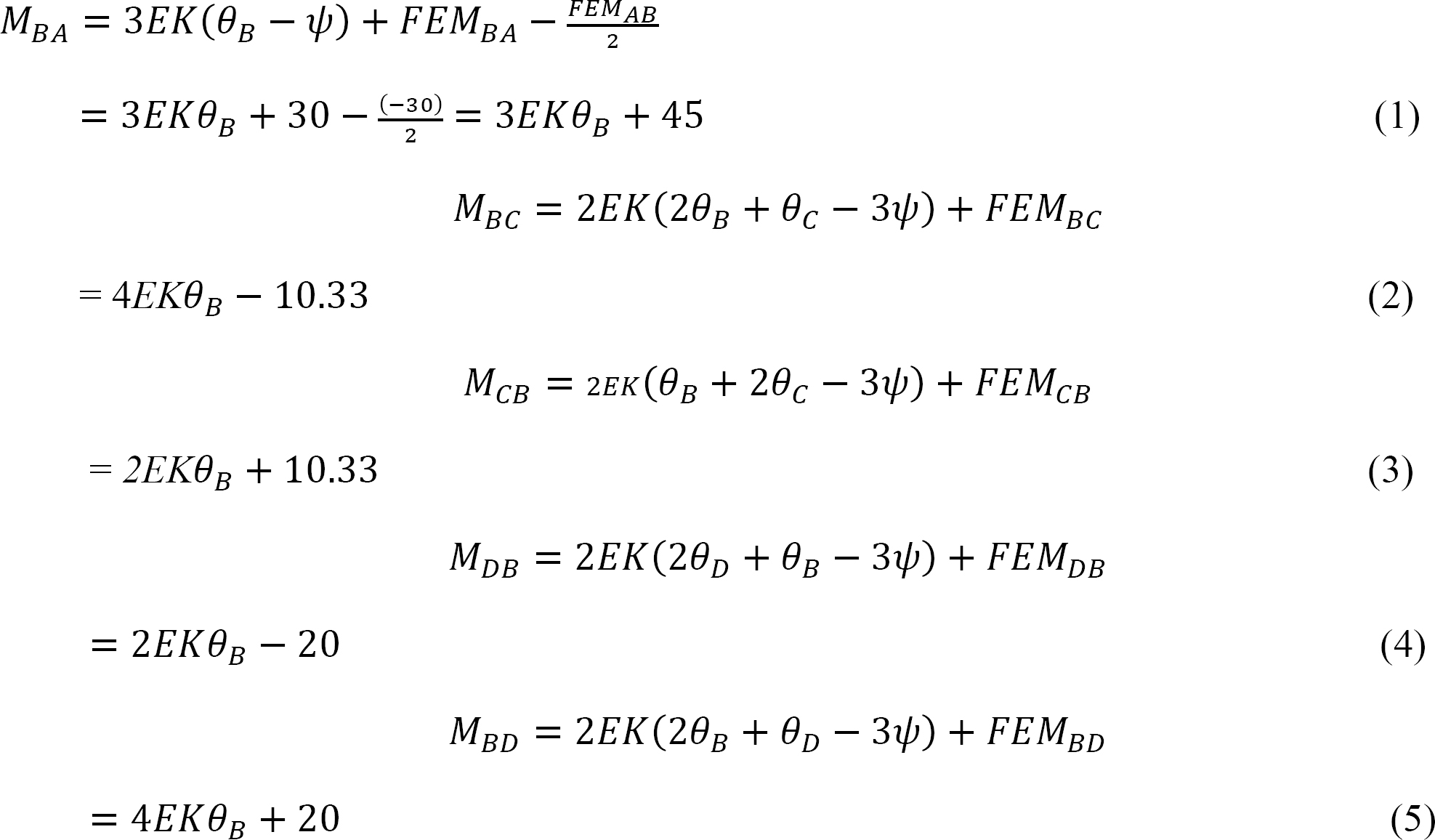
Joint equilibrium equation.
The equilibrium equation at joint B is as follows:
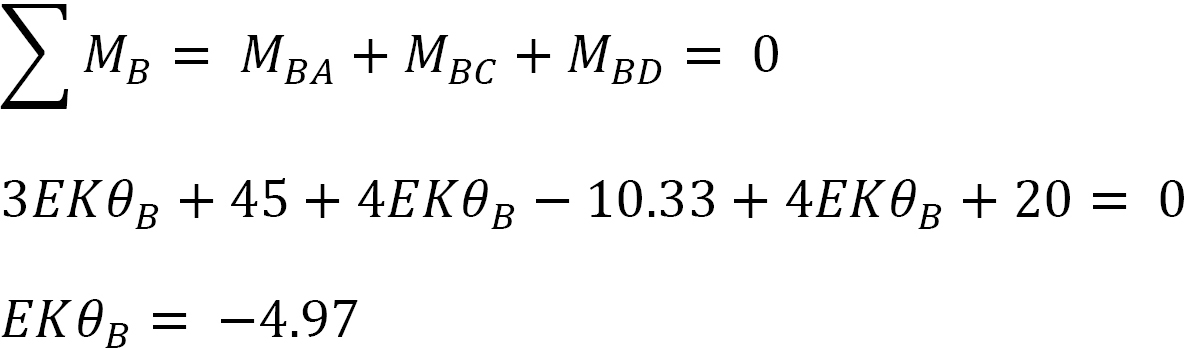
Final end moments.
Substituting EKθB = –4.97 into equations 1, 2, 3, 4, and 5 suggests the following:

MBD = 0.12 kN. m
Example 11.7
Using the slope-deflection method, determine the member end moments of the frame shown in Figure 11.13a.
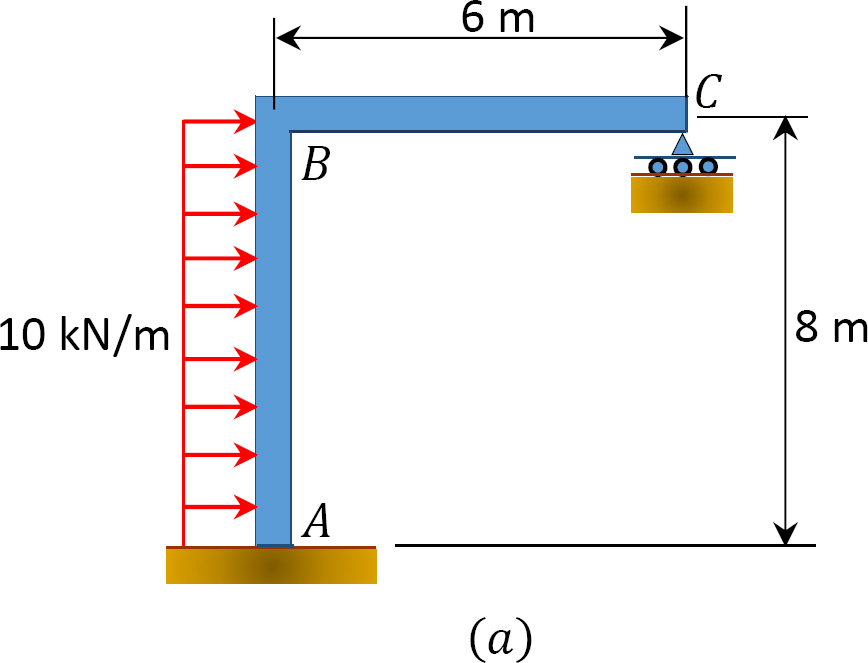
Solution
Fixed-end moments.
The Fixed-end moments (FEM) using Table 11.1 are computed as follows:
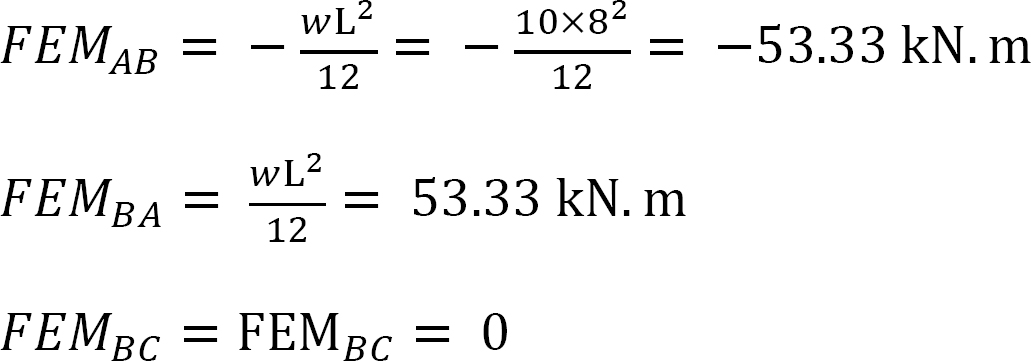
Slope-deflection equations.
As 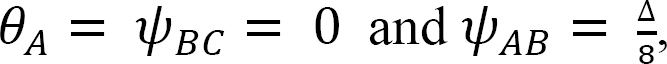 the equations for member end moments can be expressed as follows:
the equations for member end moments can be expressed as follows:
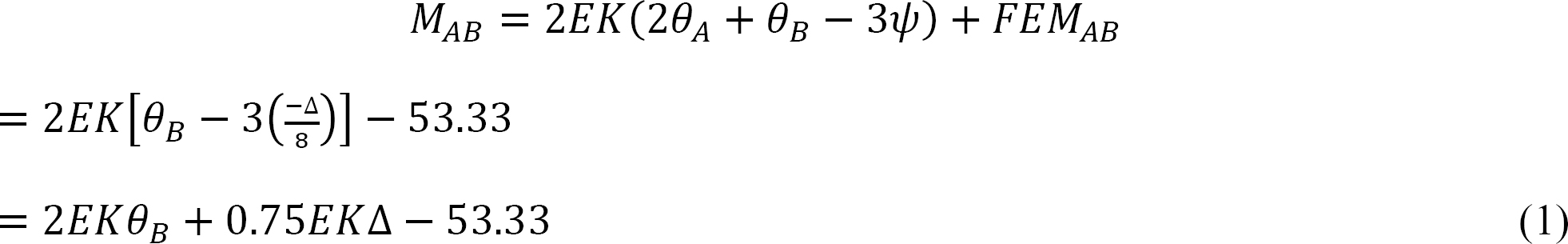
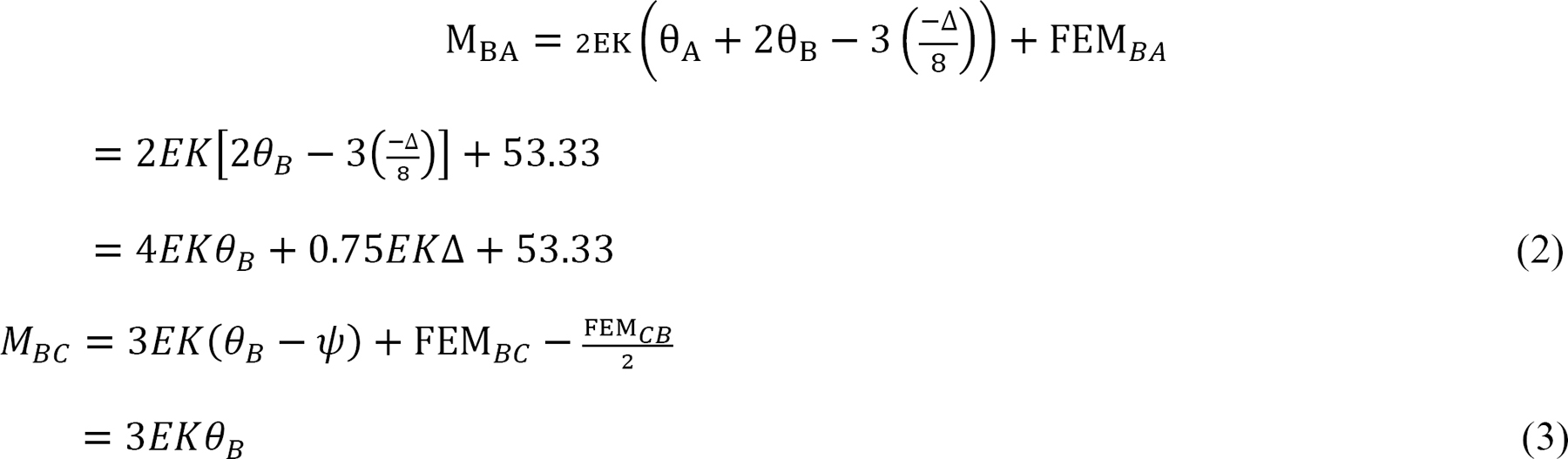
Joint equilibrium equation.
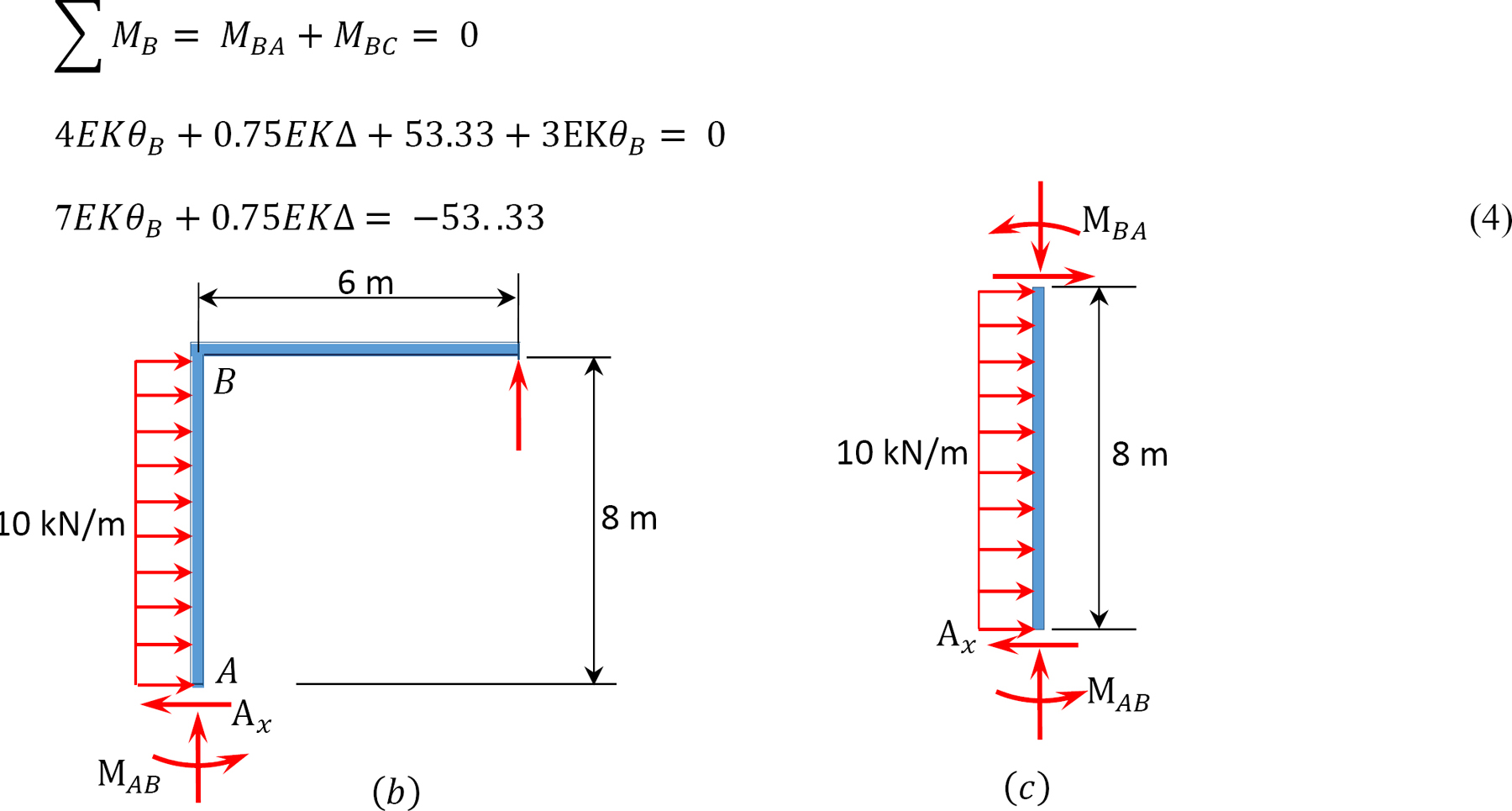


Substituting Ax from equation 6 into equation 5 suggests the following:

Substituting MAB and MBA from equations 1 and 2 into equation 7 suggests the following:
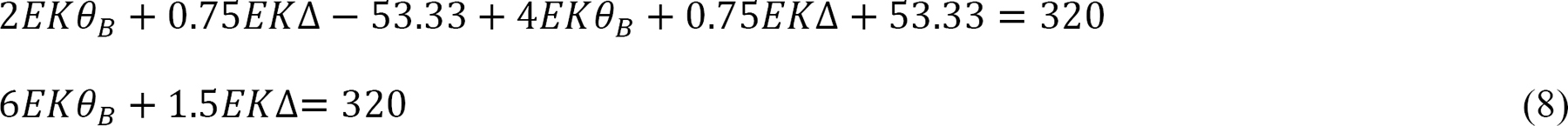
Solving equations 4 and 8 simultaneously suggests the following:
EKθB = –53.33 and EK∆ = 426.66
Final member end moments.
Putting the obtained values of EKθB and EK∆ into equations 1, 2, and 3 for member end moments suggests the following:
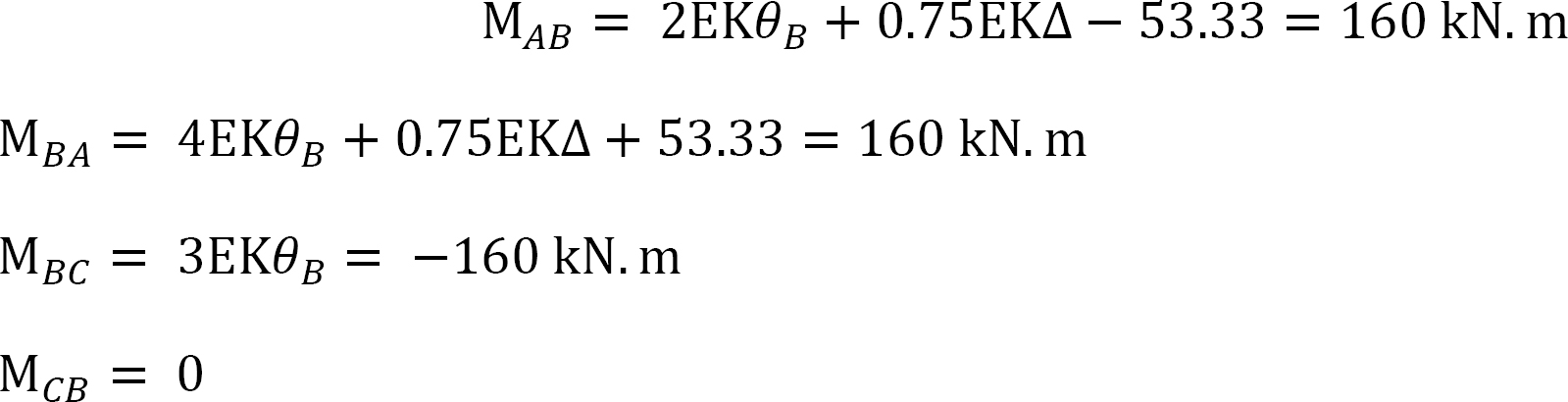
Example 11.8
Using the slope-deflection method, determine the member end moments of the beam of the rectangular cross section shown in Figure 11.14a.
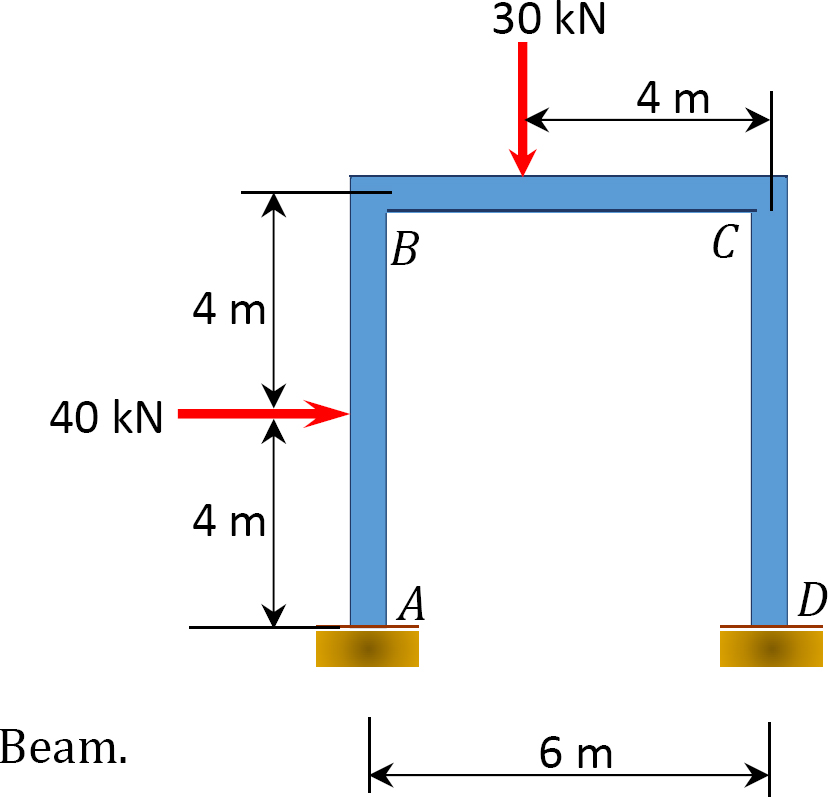
Solution
Fixed-end moments.
The Fixed-end moments (FEM) using Table 11.1 are computed as follows:
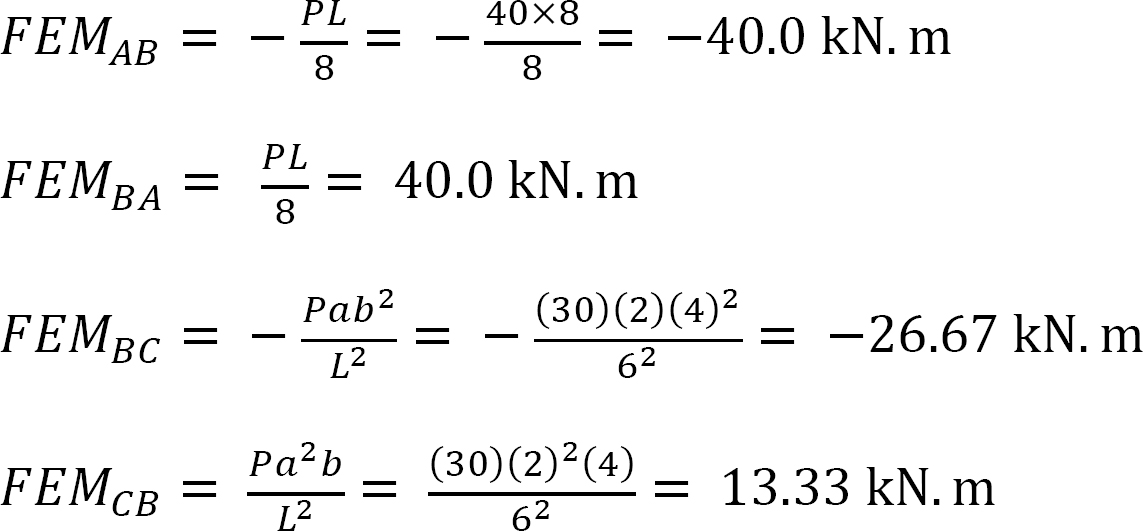
Slope-deflection equations.
As 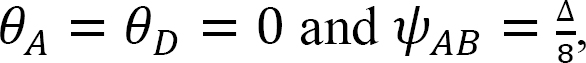 equations for member end moments can be expressed as follows:
equations for member end moments can be expressed as follows:
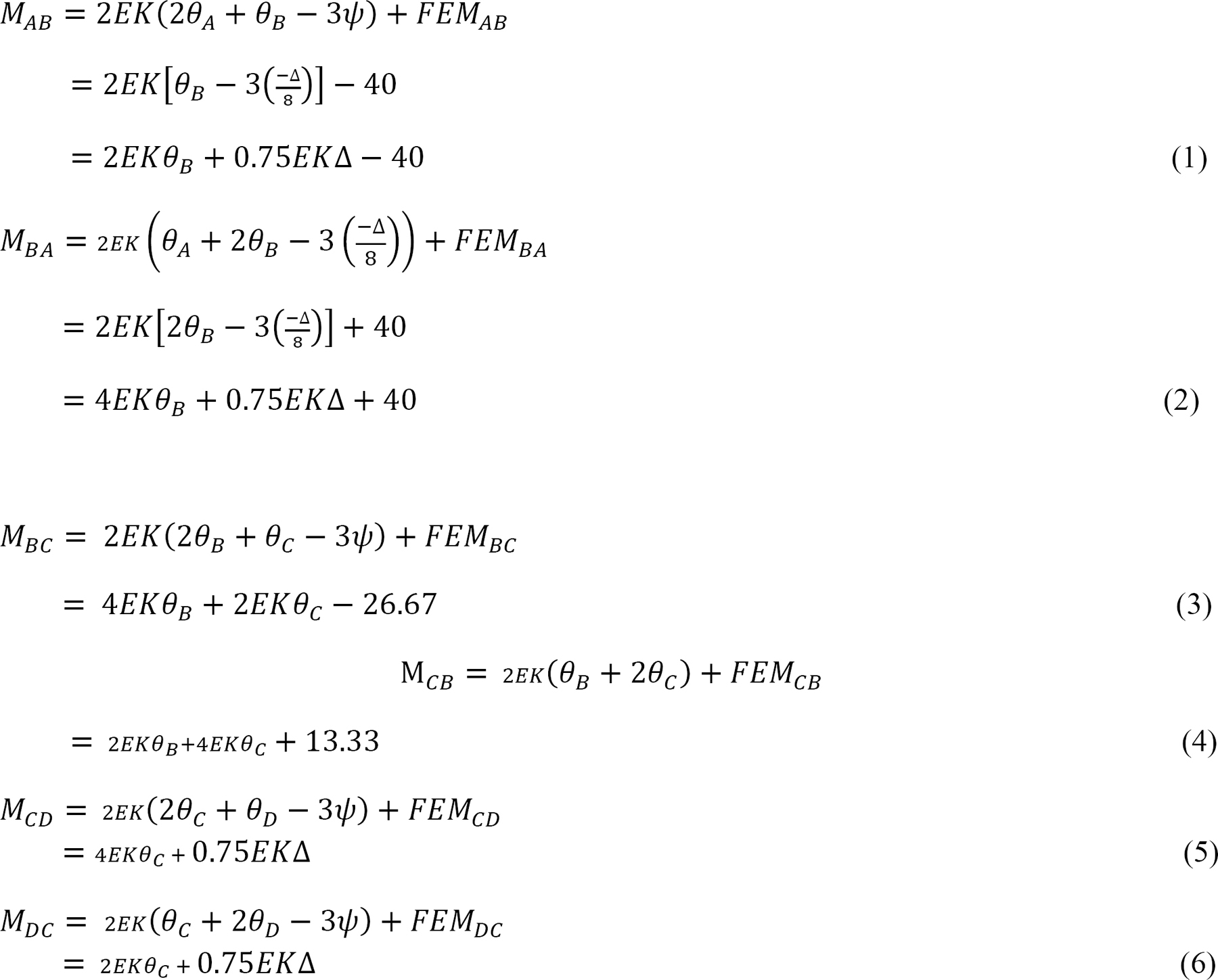
Joint equilibrium equation.
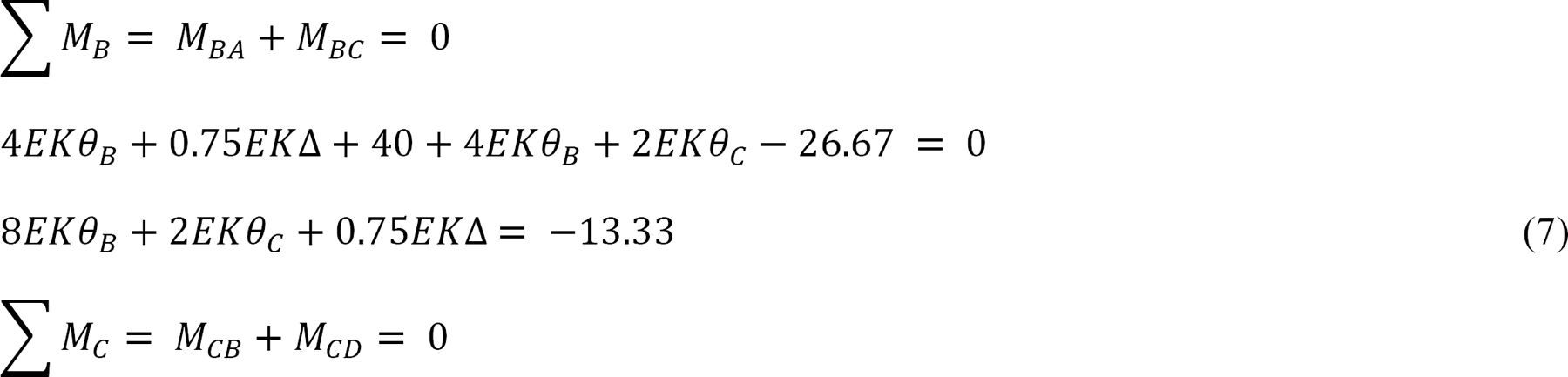
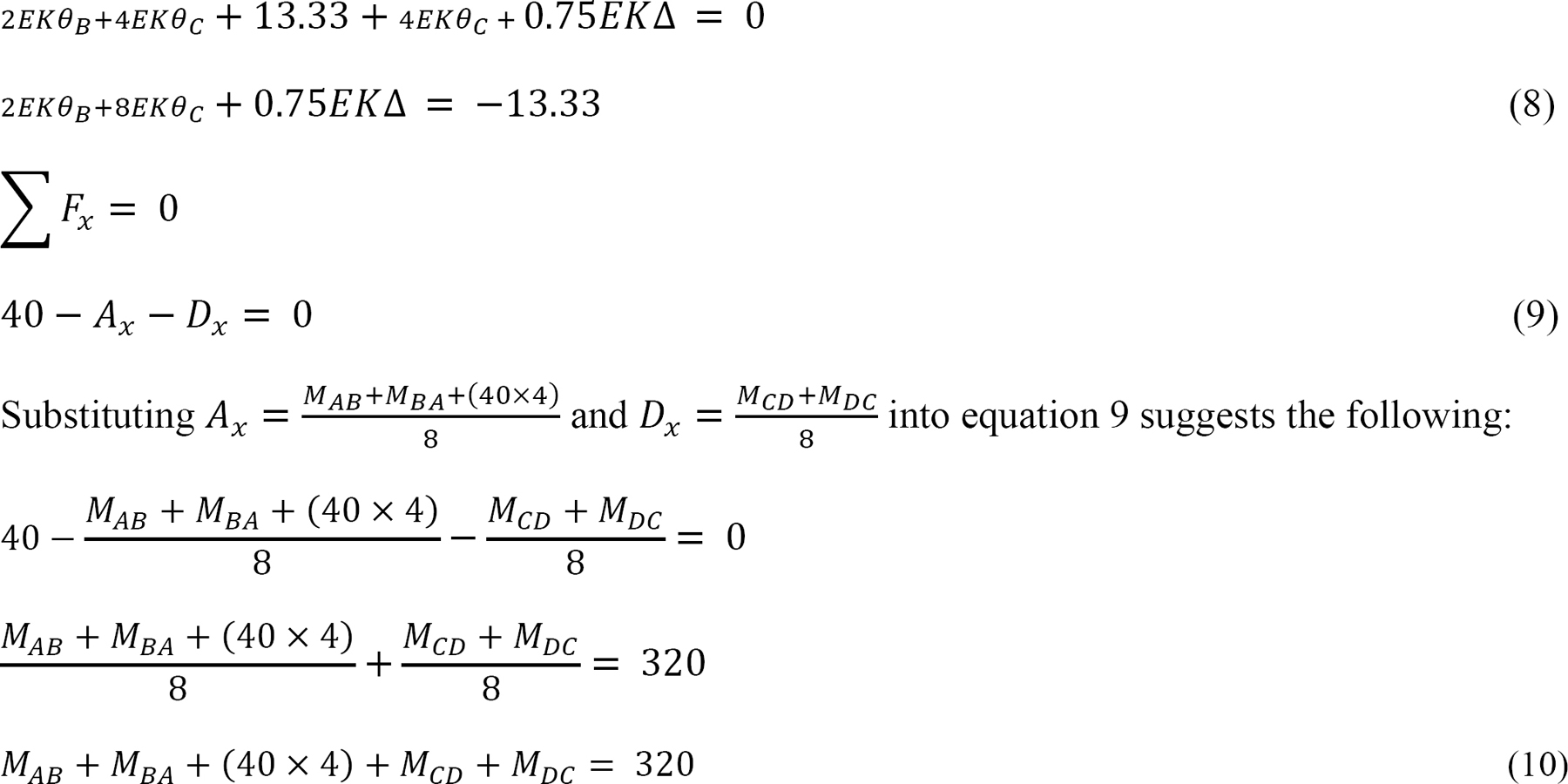
Substituting the expressions of MAB, MBA, MCD and MDC from equations 1, 2, 5, and 6 into e suggests the following:
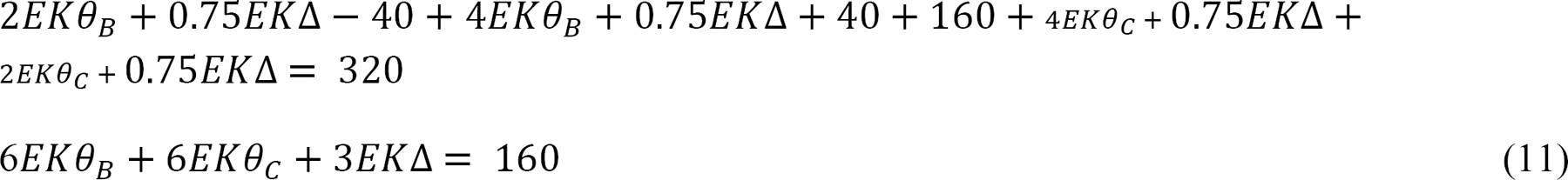
Solving equations 7, 8, and 11 simultaneously suggests the following:
EKθB = –7.62
EKθC = –7.62
EK∆= 83.81
Final member end moments.
Substituting the obtain values of EKθB, EKθC and EK∆ into member end moment equations suggests the following:
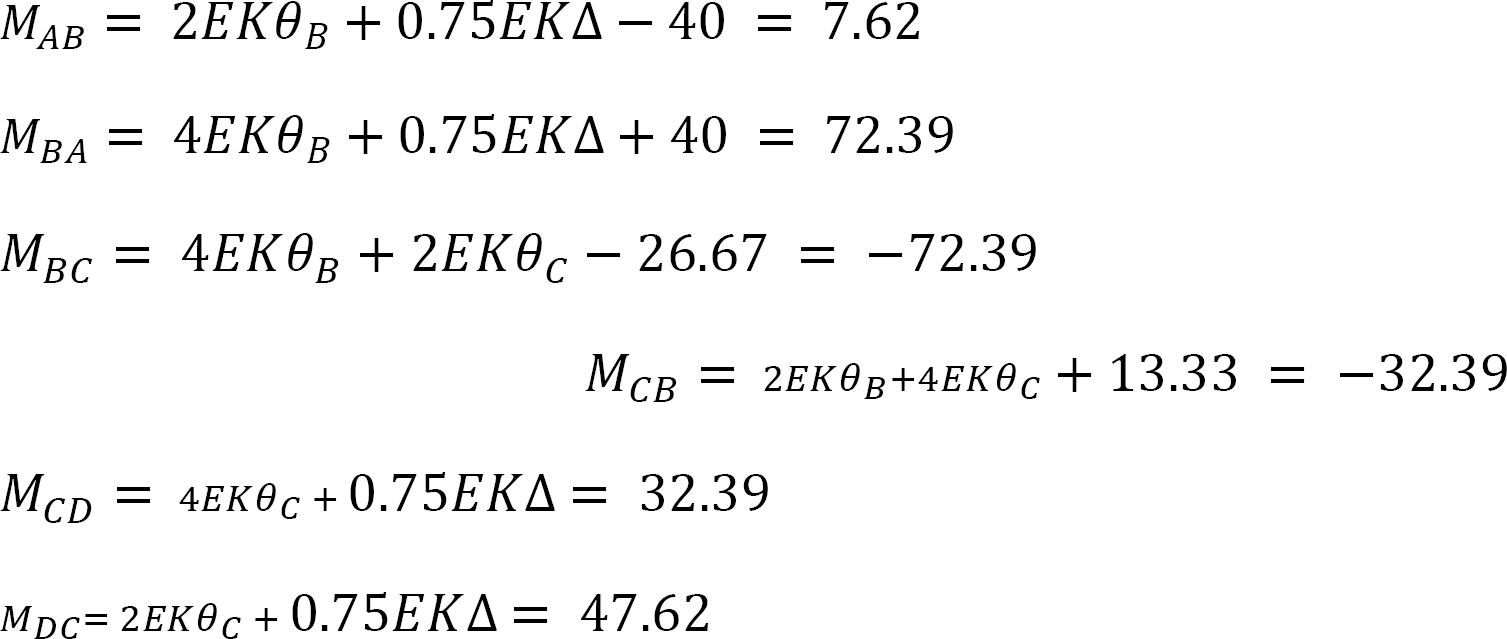
Table 11.1. Fixed-end moments.
Chapter Summary
Slope-deflection method of analysis of indeterminate structures: The unknowns in the slope-deflection method of analysis are the rotations and the relative displacements. Slope-deflection equations for member-end moments and the equilibrium equation at each joint that is free to rotate are written in terms of the rotations and relative displacements, and they are solved simultaneously to determine the unknowns. When the unknown rotations and the relative displacements are determined, they are put back in member end moment equations to determine the magnitude of the moments. After determination of the end moments, the structure becomes determinate. The detailed procedures for analysis by slope-deflection method for beams and frames are presented in sections 11.5 and 11.6. In situations where there are several unknowns, analysis using this method can be very cumbersome, hence the availability of software that can perform the analysis.
Slope-deflection equations for mnd Moments:
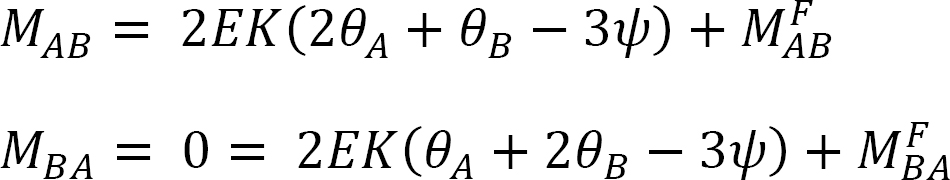
Modified slope-deflection equation when far end is supported by a roller or pin:
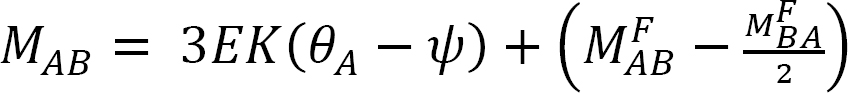
Practice Problems
11.1 Using the slope-deflection method, compute the end moment of members of the beams shown in Figure P11.1 through Figure P11.5 and draw the bending moment and shear force diagrams. EI = constant.
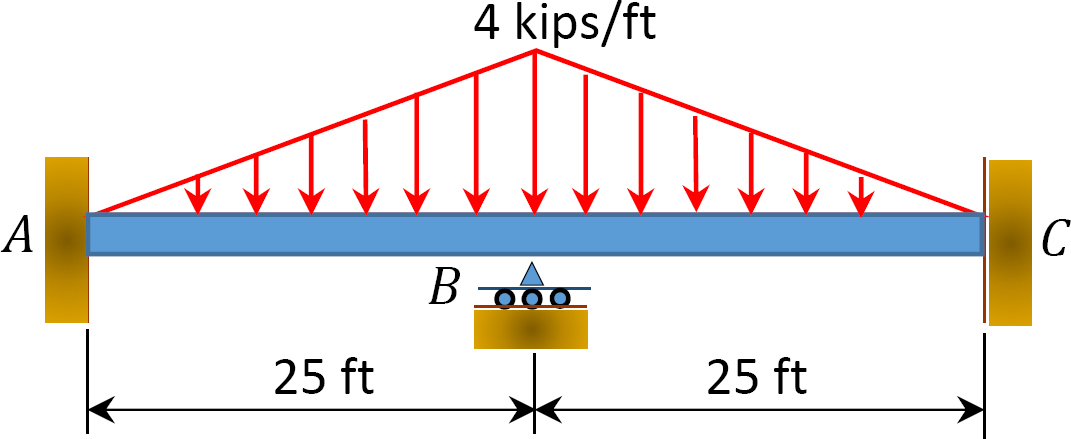
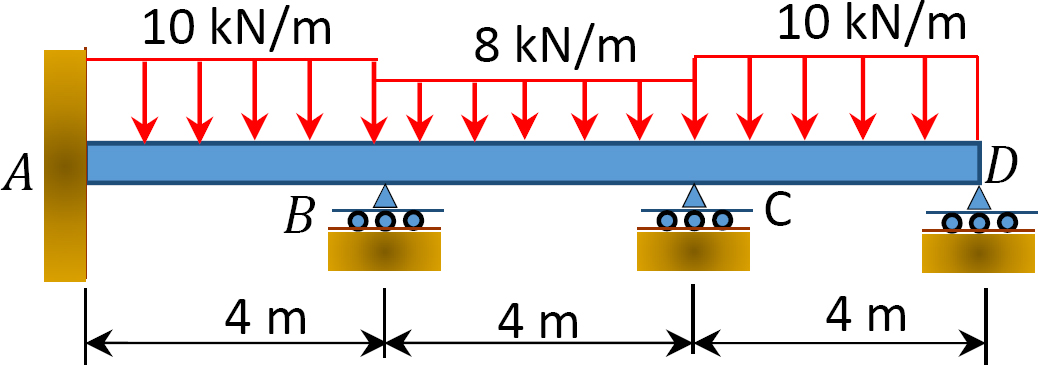
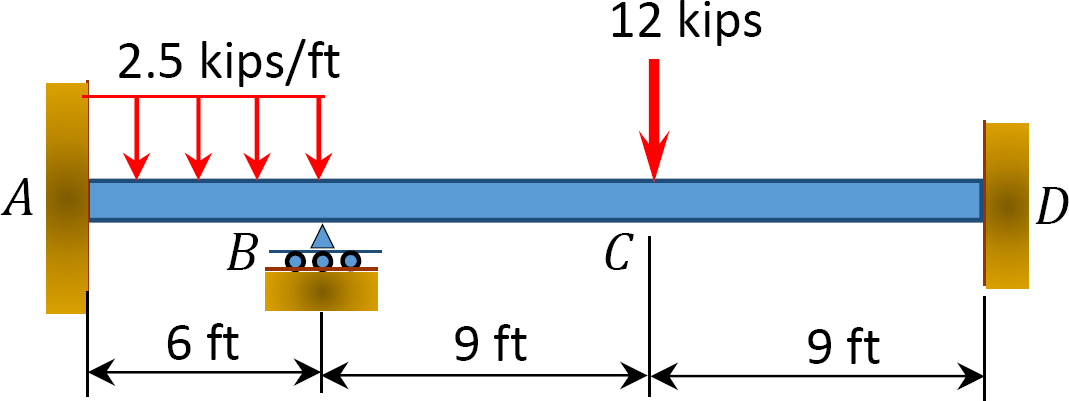
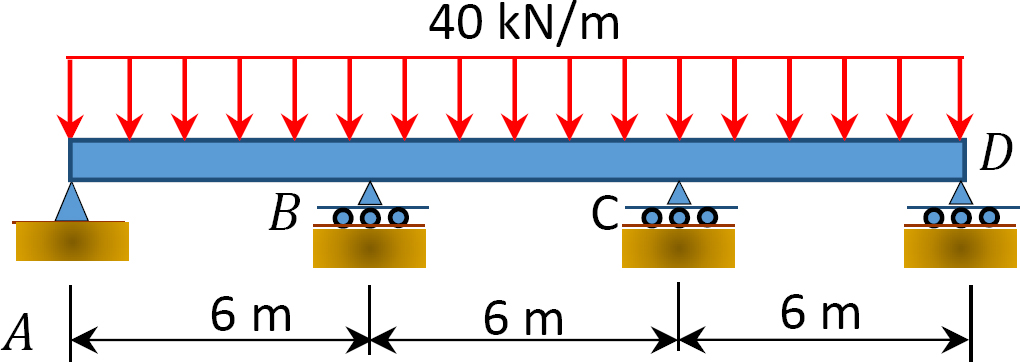
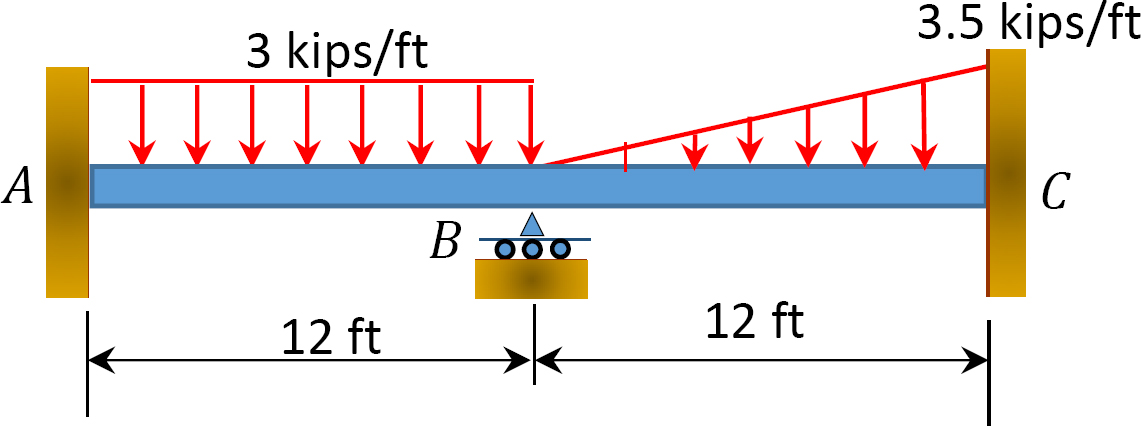
11.2 Using the slope-deflection method, compute the end moments of members of the beams shown in Figure P11.6. Assume support E settles by 50 mm. E = 200 GPa and I = 600 × 106mm4.
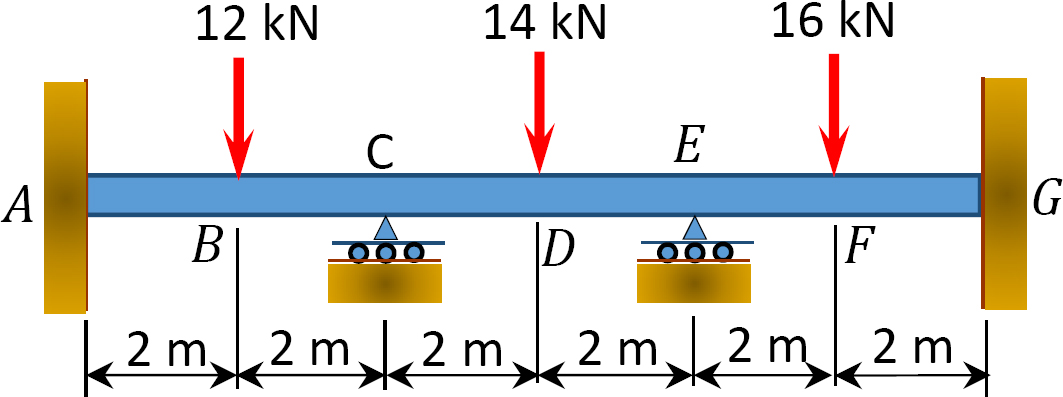
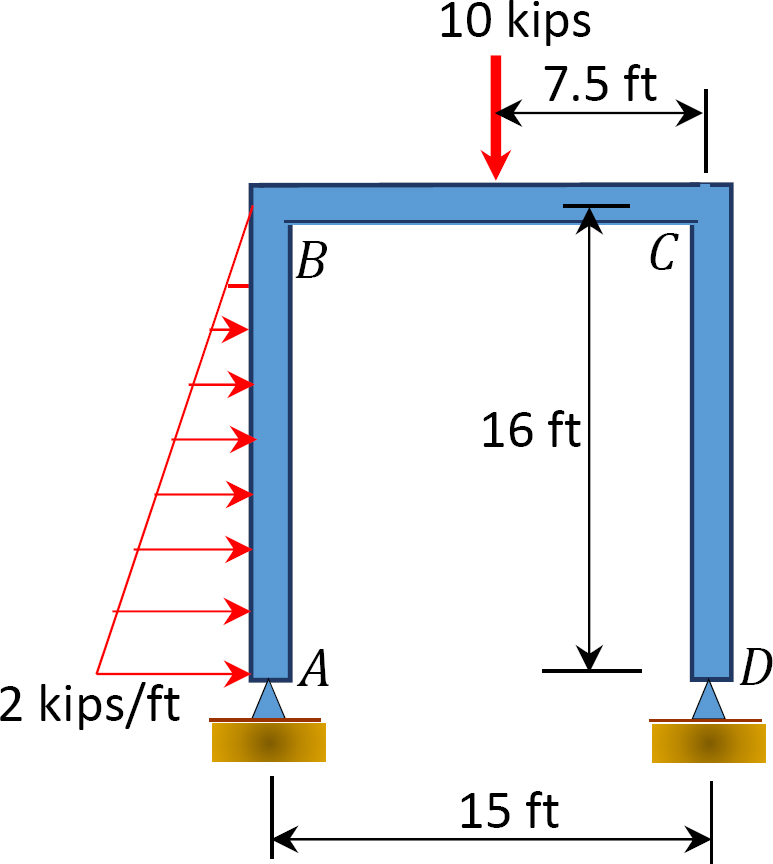
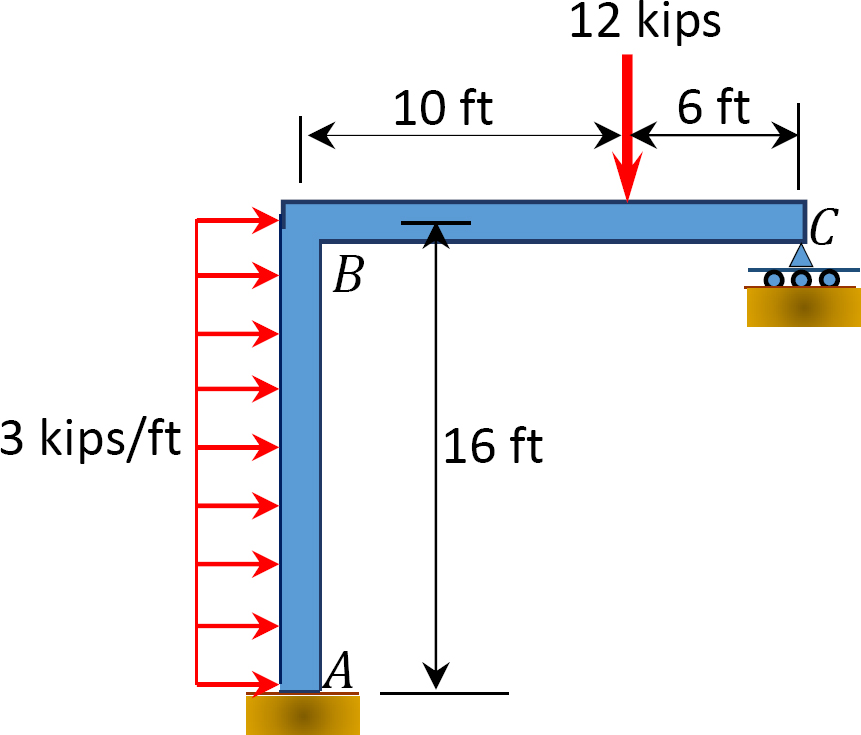
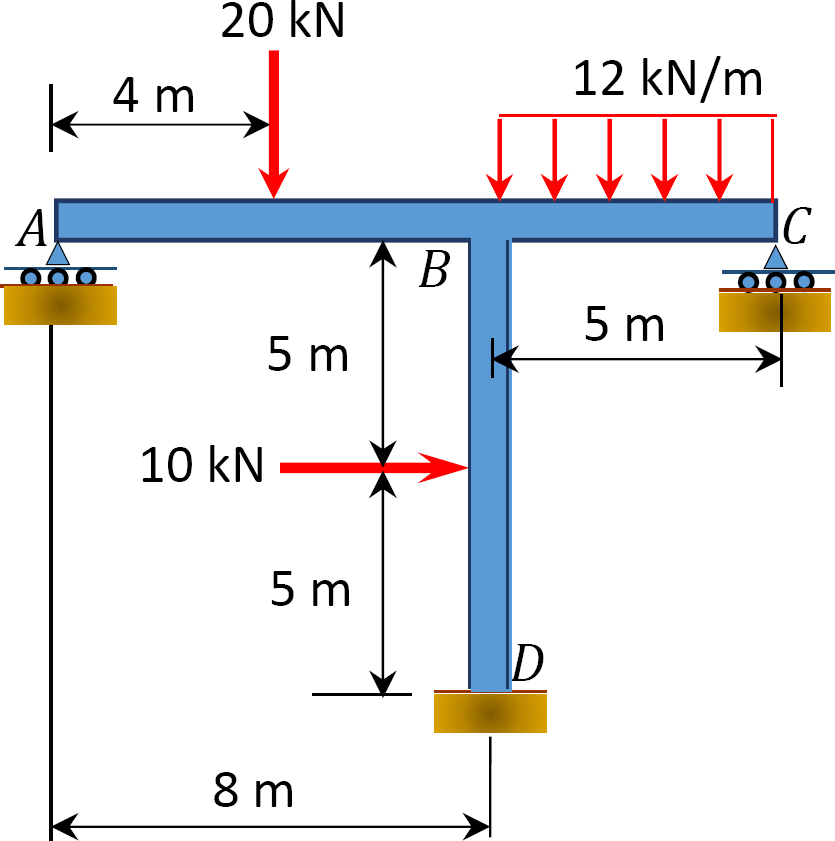
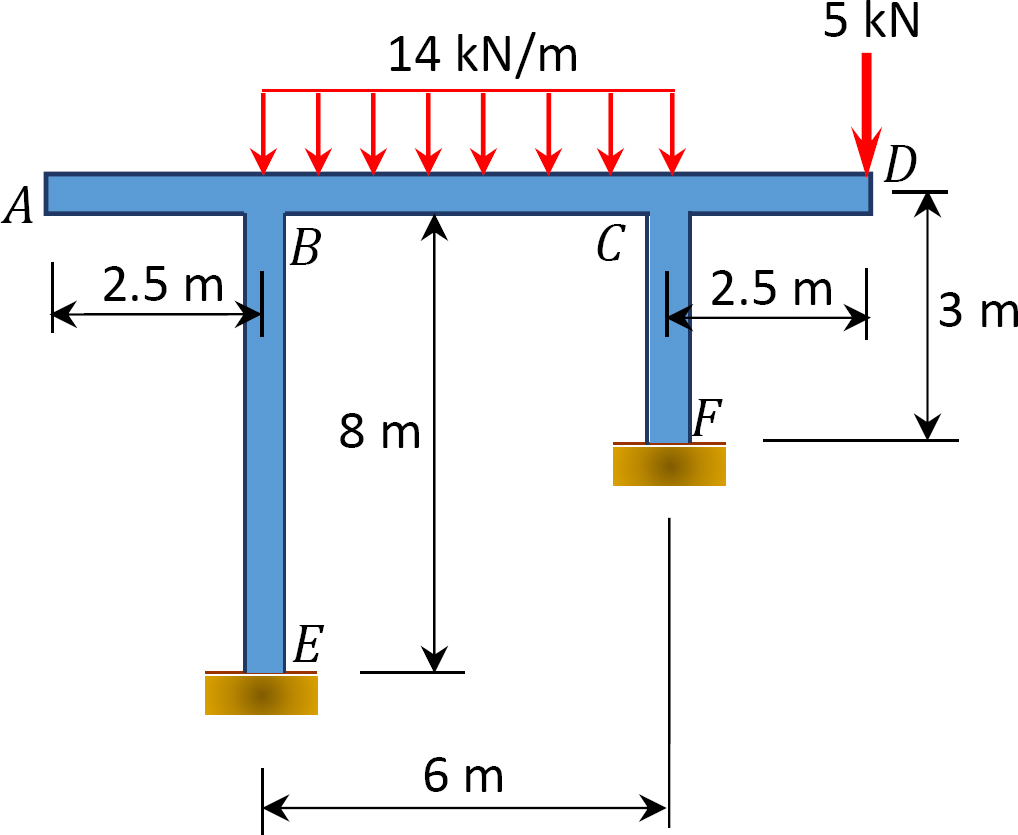
11.3 Using the slope-deflection method, determine the end moments of the members of the non-sway frames shown in Figure P11.7 through Figure P11.10. Draw the bending moment and the shear force diagrams.
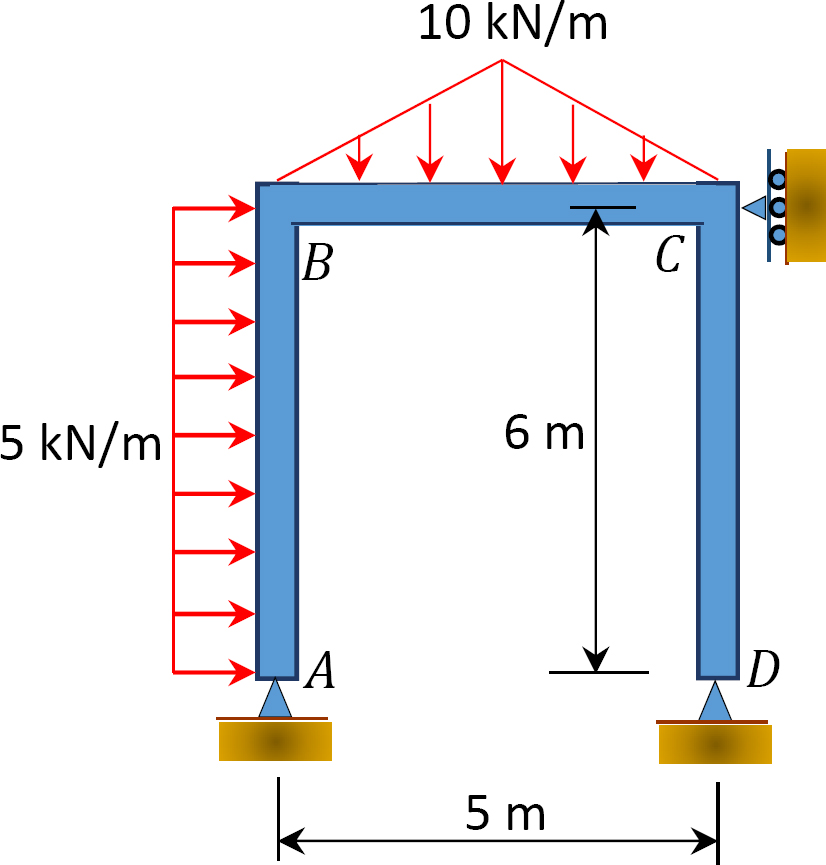
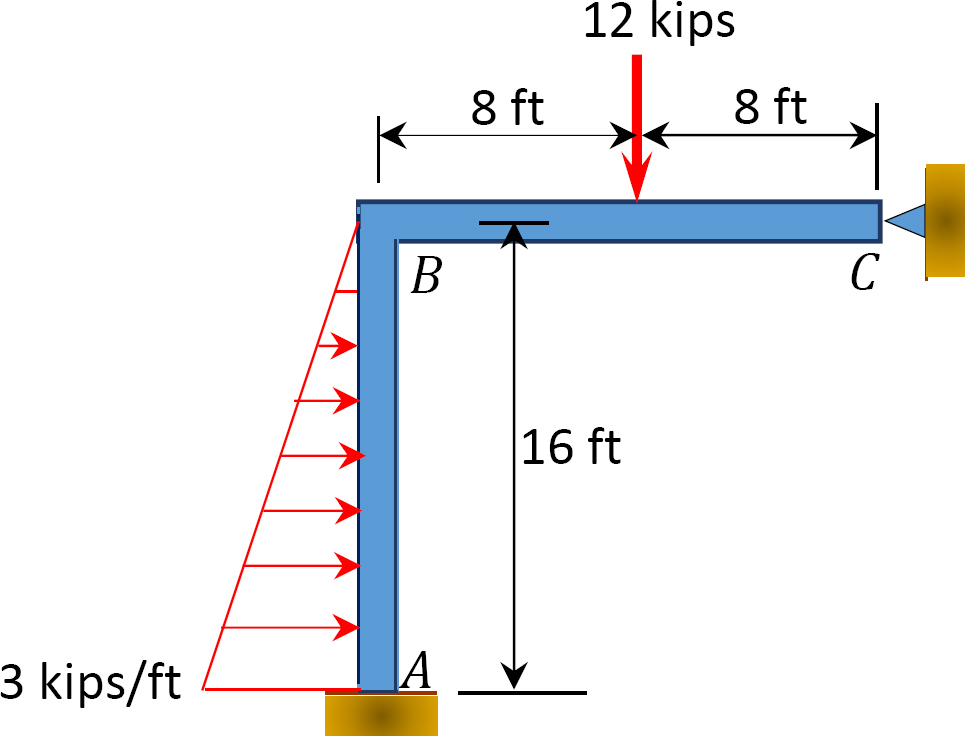
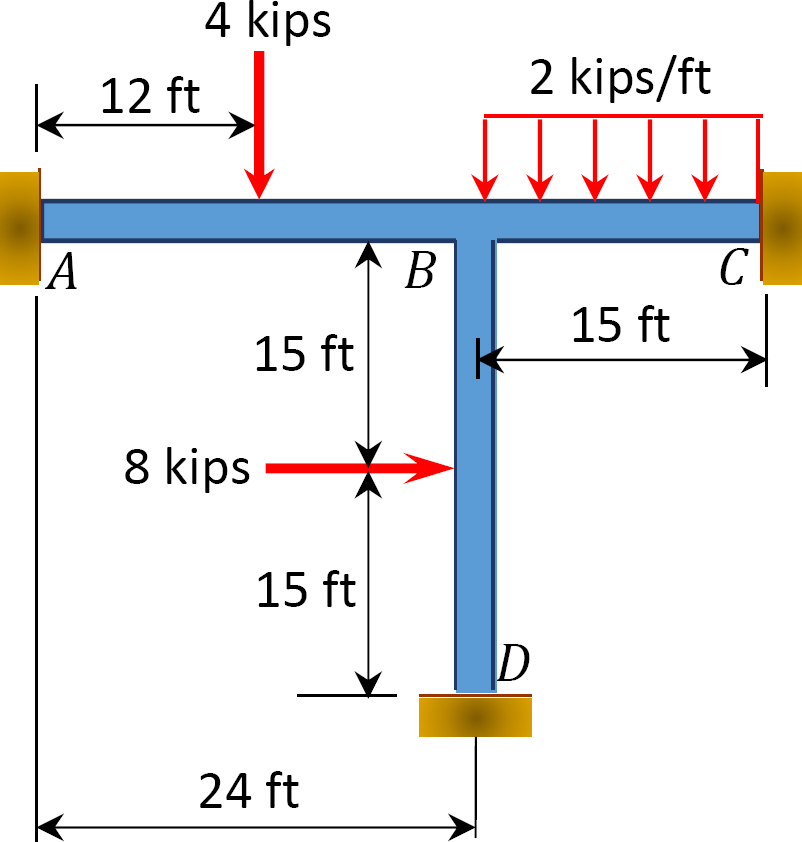
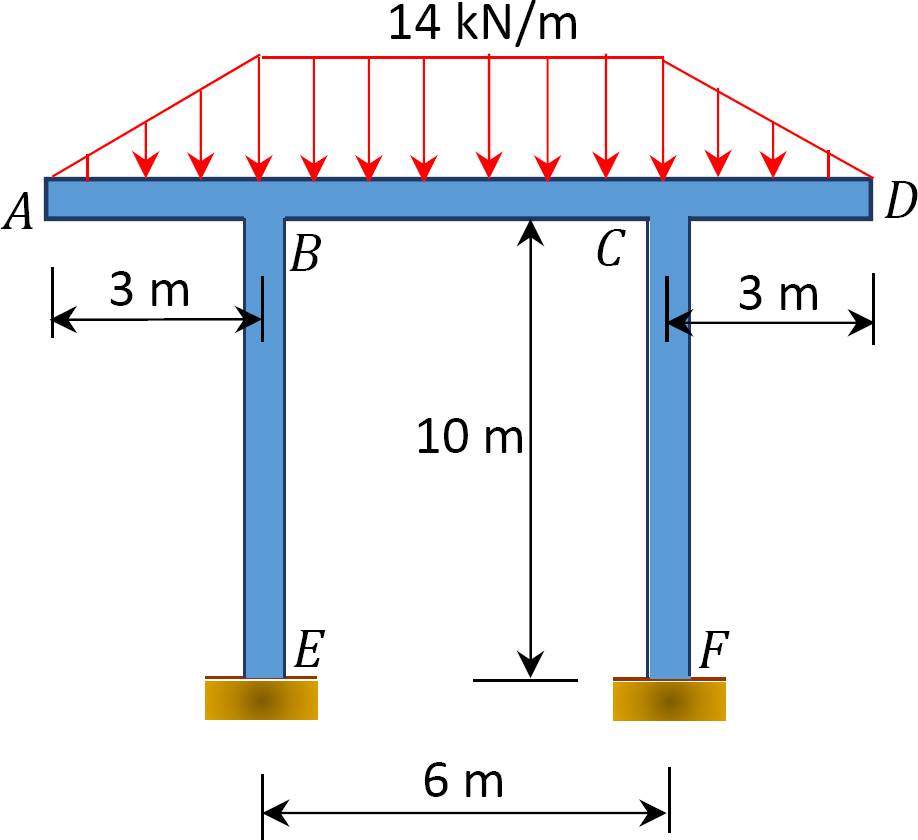
11.4 Using the slope-deflection method, determine the end moments of the members of the sway frames shown in Figure P11.11 through Figure P11.14. Draw the bending moment and the shear force diagrams.