1.12: Moment Distribution Method of Analysis of Structures
- Page ID
- 17619
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)12.1 Basic Concepts
The moment distribution method of analysis of beams and frames was developed by Hardy Cross and formally presented in 1930. Although this method is a deformation method like the slope-deflection method, it is an approximate method and, thus, does not require solving simultaneous equations, as was the case with the latter method. The degree of accuracy of the results obtained by the method of moment distribution depends on the number of successive approximations or the iteration process.
To illustrate the concept of the method of moment distribution, consider the frame shown in Figure 12.1. Members of the frame are prismatic and are assumed not to deform axially nor translate relative to one another. Joints ACD of the frame are fixed, while joint B can rotate slightly due to the applied load. First, before carrying out moment distribution among members, all the joints are assumed to be temporarily locked using a clamp.

12.2 Sign Convention
The sign convention for the moment distribution method is similar to the one established for the slope-deflection method; that is, the moment at the end of a member is considered positive if it tends to turn the end of the member clockwise and negative if it tends to turn it counterclockwise.
12.3 Definitions
Unbalanced moments: This method of analysis assumes that the joints in a structure are initially clamped or locked and then released successively. Once a joint is released, a rotation takes place, since the sum of the fixed end moments of the members meeting at that joint is not zero. The value of the sum of the end moments obtained is the unbalanced moment at that joint.
Carry-over moments: The distributed moments in the ends of members meeting at a joint cause moments in the other ends, which are assumed to be fixed. These induced moments at the other ends are called carry-over moments.
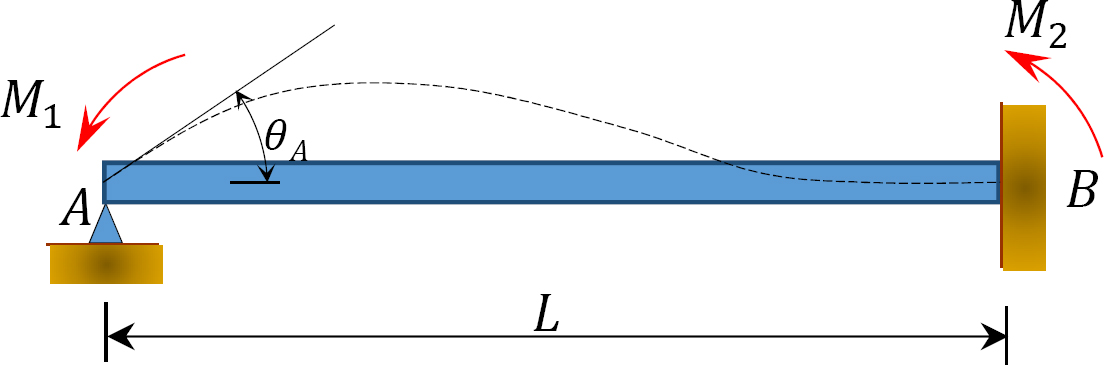
Consider an unloaded prismatic beam fixed at end B, as shown in Figure 12.2. If a moment M1 is applied to the left end of the beam, the slope-deflection equations for both ends of the beam can be written as follows:
\[M_{1}=2 E K\left(2 \theta_{A}\right)=4 E K \theta_{A} \label{12.1}\]
\[M_{2}=2 E K \theta_{A} \label{12.2}\]
Substituting \(\theta_{A}=\frac{M_{1}}{4 E K}\) from Equation \ref{12.1} into Equation \ref{12.2} suggest the following:
\[M_{2}=\frac{1}{2} M_{1} \label{12.3}\]
Equation \ref{12.3} suggests that the moment carried over to the fixed end of a beam due to a moment applied at the other end is equal to one-half of the applied moment.
Carry-over factor: The ratio of the induced moment to the applied moment is referred to as the carry-over factor. For the beam shown in Figure 12.2, the carry-over factor is as follows:
\[\frac{M_{2}}{M_{1}}=\frac{2 E K \theta_{A}}{4 E K \theta_{A}}=\frac{1}{2} \label{12.4}\]
Distributed factor (DF): The distributed factor is a factor used to determine the proportion of the unbalanced moment carried by each of the members meeting at a joint. For the members meeting at joint O of the frame shown in Figure 12.3, their distribution factors are computed as follows:
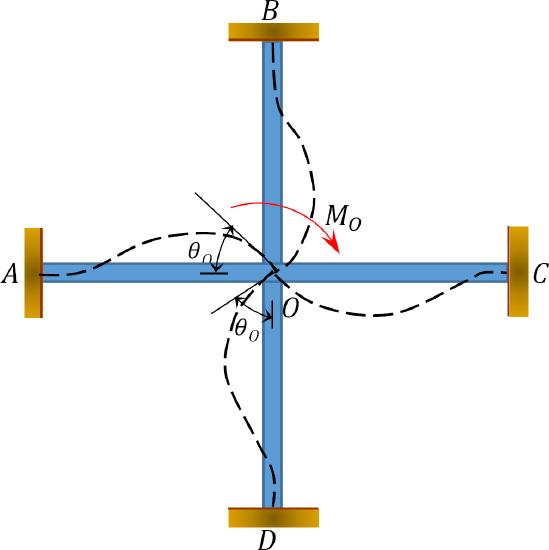
\[\begin{aligned}
&(D F)_{O A}=\frac{K_{O A}}{\Sigma K} \\
&(D F)_{O B}=\frac{K_{O B}}{\sum K} \\
&(D F)_{O C}=\frac{K_{O C}}{\Sigma K} \\
&(D F)_{O D}=\frac{K_{O D}}{\sum K}
\end{aligned} \label{12.5}\]
Distributed moments: Upon the release of the imaginary clamp at a joint, the unbalanced moment at that joint causes it to rotate. The rotation twists the end of the members meeting at the joint, resulting in the development of resisting moments. These resisting moments are called distributed moments. The distributed moments for the members of the frame shown in Figure 12.3 are computed as follows:
\[\begin{aligned}
M_{O A} &=\frac{K_{O A}}{\sum K} M_{O}=(D F)_{O A} M_{O} \\
M_{O B} &=\frac{K_{O B}}{\sum K} M_{O}=(D F)_{O B} M_{O} \\
M_{O C} &=\frac{K_{O C}}{\sum K} M_{O}=(D F)_{O C} M_{O} \\
M_{O D} &=\frac{K_{O D}}{\sum K} M_{O}=(D F)_{O D} M_{O}
\end{aligned} \label{12.6}\]
12.4 Modification of Member Stiffness
Sometimes the iteration process in the moment distribution method can be significantly reduced by adjusting the flexural stiffness of some members of the indeterminate structure. This section considers the influence of a fixed- and a pin-end support on the flexural stiffness of an indeterminate beam.
Case 1: A beam hinged at one end and fixed at the other
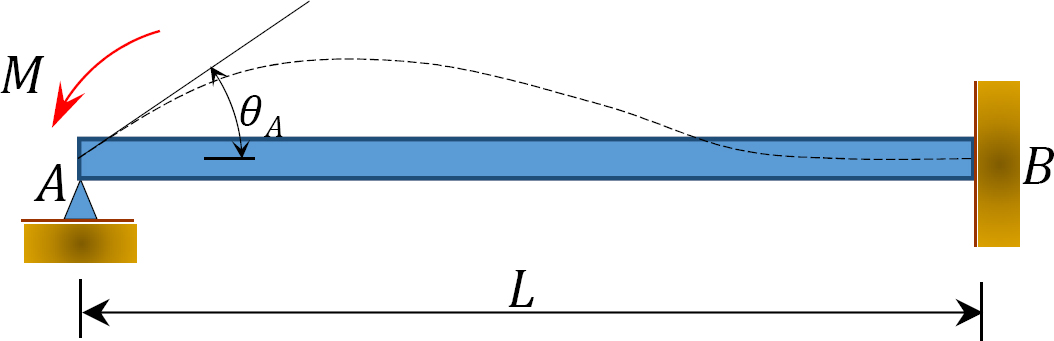
Consider a beam hinged at end A and fixed at end B, as shown in Figure 12.4. Applying a moment M rotates the hinge end by an amount \(θ\). Writing the slope-deflection equation for the end A of the member and noting that
\[\theta_{B}=\psi_{A B}=M_{A B}^{F}=0 \nonumber\]
suggests the following:
\[\begin{align*}
M_{A B} &=\frac{2 E I}{L}\left(2 \theta_{A}+\theta_{B}-3 \psi_{A B}\right)+M_{A B}^{F} \\
&=\frac{2 E I}{L}\left(2 \theta_{A}+0-0\right)+0
\end{align*}\]
\[M_{A B}=\left(\frac{4 E I}{L}\right) \theta_{A} \lbael{12.7}\]
By definition, the bending stiffness of a structural member is the moment that must be applied to an end of the member to cause a unit rotation of that end. The following expression for the bending stiffness for the member with a fixed far end is expressed as follows when substituting θA = 1 into Equation \ref{12.7}:
\[K=\frac{4 E I}{L} \label{12.8}\]
By definition, the relative bending stiffness of a member is determined by dividing the bending stiffness of the member by 4E. Dividing the Equation \ref{12.8} by 4E suggests the following expression for relative stiffness for the case being considered:
\[K_{R}=\frac{4 E I}{4 E L}=\frac{I}{L} \label{12.9}\]
Case 2: A beam hinged at both ends
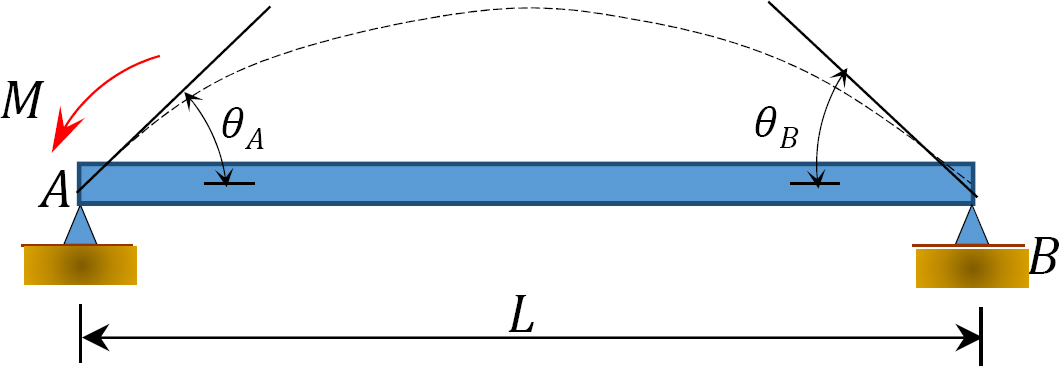
Applying a moment M at the end A of the simply supported beam shown in Figure 12.5 rotates the beam by an angle θA at the hinged end. Using the modified slope-deflection equation derived in section 11.4 of Chapter 11 and noting that
\[\psi=M_{A B}^{F}=M_{B A}^{F}=0 \nonumber\]
suggests the following expression for the moment at the hinged end where the load is applied:
\[\begin{align*} M_{A B}&=\frac{3 E I}{L}\left(\theta_{A}-\psi\right)+\left(M_{A B}^{F}-\frac{M_{B A}^{F}}{2}\right) \\[4pt] &=\frac{3 E I}{L}\left(\theta_{A}-0\right)+(0-0)\end{align*} \]
\[M_{A B}=\left(\frac{3 E I}{L}\right) \theta_{A} \label{12.10}\]
Substituting θA = 1 into Equation \rer{12.10} suggests the following expression for the bending stiffness for a member with a hinged far end:
\[K=\frac{3 E I}{L} \label{12.11}\]
The relative stiffness for a member with a hinged far end is obtained by dividing Equation \ref{12.11} by \(4E\), as follows:
\[K_{R}=\frac{3 E I}{4 E L}=\frac{3}{4}\left(\frac{I}{L}\right) \label{12.12}\]
Comparing equations \ref{12.12} and \ref{12.9} suggests that a member with a hinged far end is three-fourth as stiff as a member with the same geometry but fixed at the far end. This established fact can substantially reduce the number of iteration when analyzing beams or frames with a hinged far end using the method of moment distribution. In such cases, the relative stiffness of the beam at the near end is first adjusted according to Equation \ref{12.12}, and its distribution factor is computed with the adjusted stiffness. During the balancing operation, the near end will be balanced just once with no further carrying over of moments from or to its end.
12.5 Analysis of Indeterminate Beams
The procedure for the analysis of indeterminate beams by the method of moment distribution is briefly summarized as follows:
Procedure for Analysis of Indeterminate Beams by the Moment Distribution Method
- Calculate the fixed-end moments for members, assuming that the joints are clamped against rotation.
- Calculate the distribution factor for each of the members connected at the joint
- Calculate the unbalanced moment at each joint and distribute the same to the ends of members connected at that joint.
- Carry over one-half of the distributed moment to the other ends of members.
- Add or subtract these latter moments (moments obtained in steps three and four) to or from the original fixed-end moments.
- Apply the determined end moments at the joints of the given structure.
- Draw the free-body diagram of each span of the given beam, showing the loads and moments at the joints obtained by the moment distribution method.
- Determine the support reactions for each span.
- Compute and construct the shearing force and bending moment diagrams for each span.
- Draw one bending moment and one shearing force diagram for the given beam by combining the diagrams in step 9.
Example 12.1
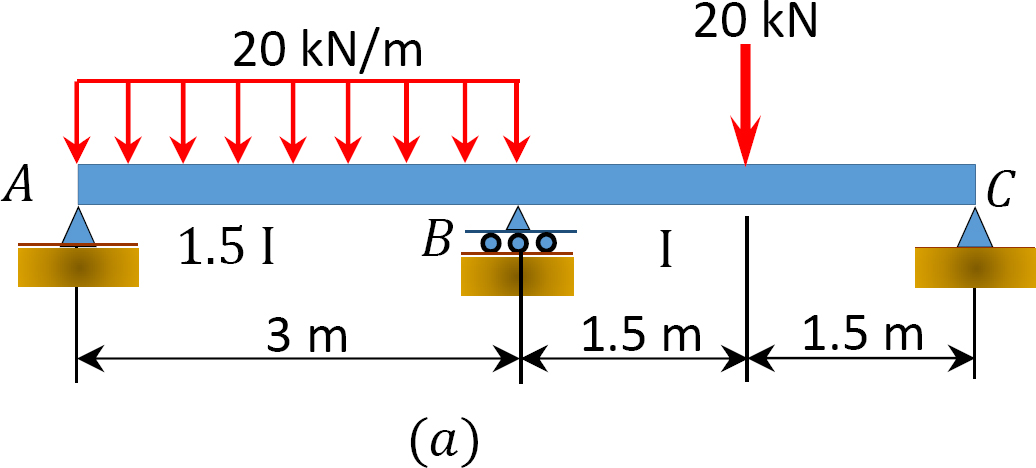
Using the moment distribution method, determine the end moments and the reactions at the supports of the beam shown in Figure 12.6a. Draw the shearing force and the bending moment diagrams. EI = constant.
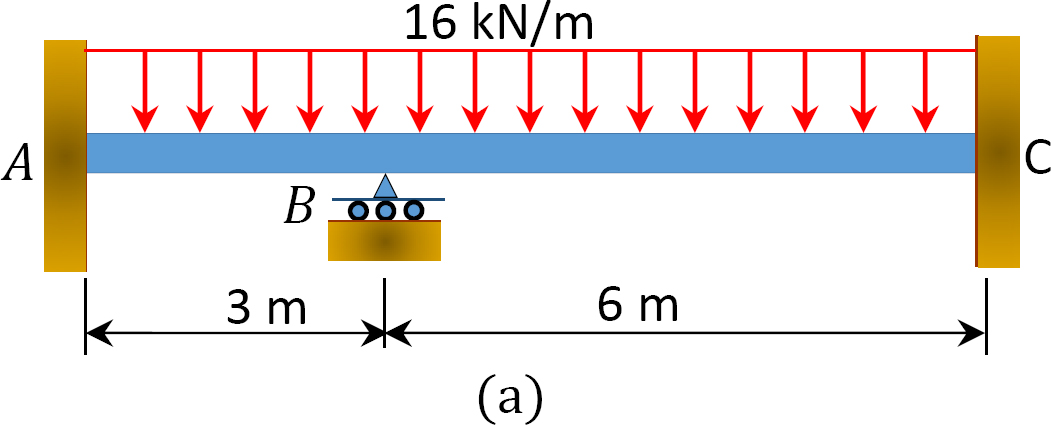
Solution
Fixed end moment.
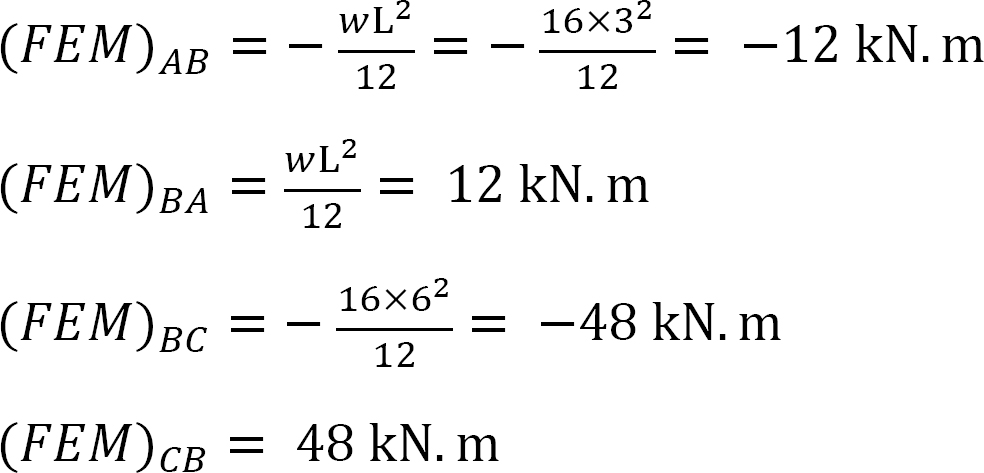
Stiffness factor.
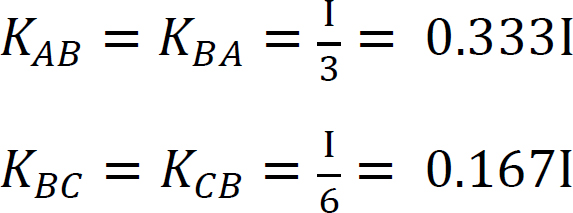
Distribution factor.
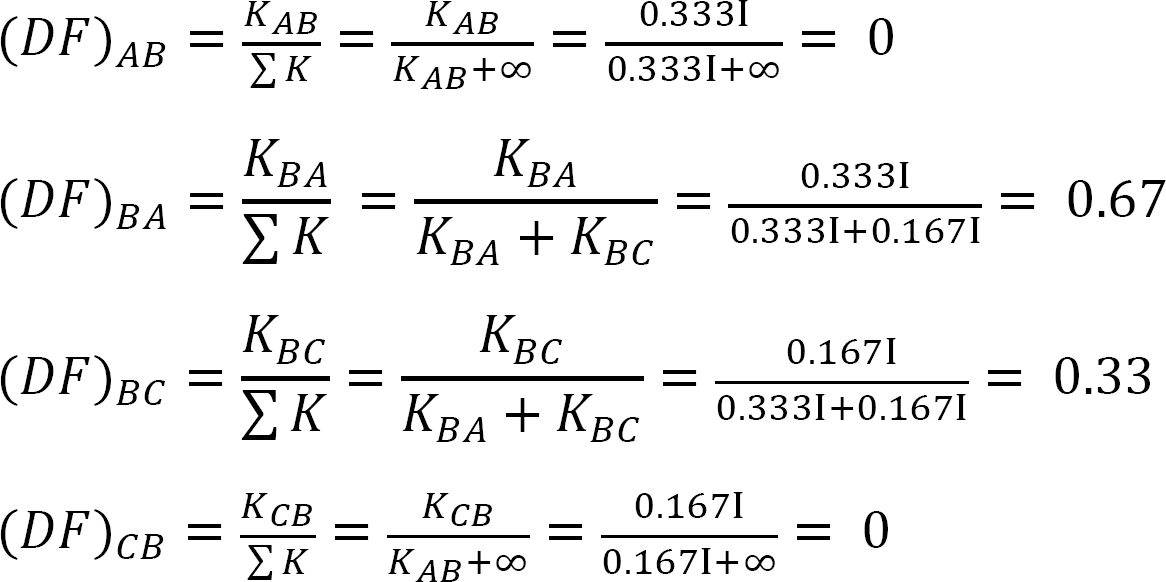
Table 12.1. Distribution table.
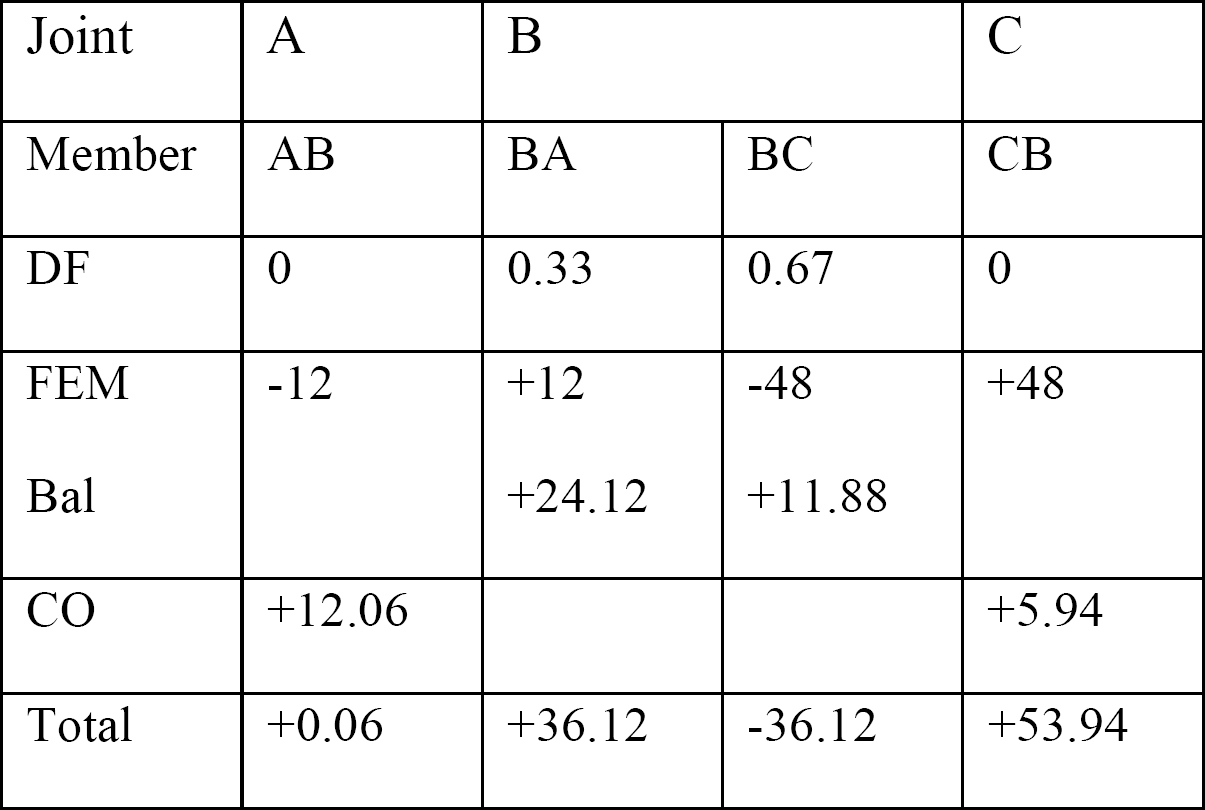
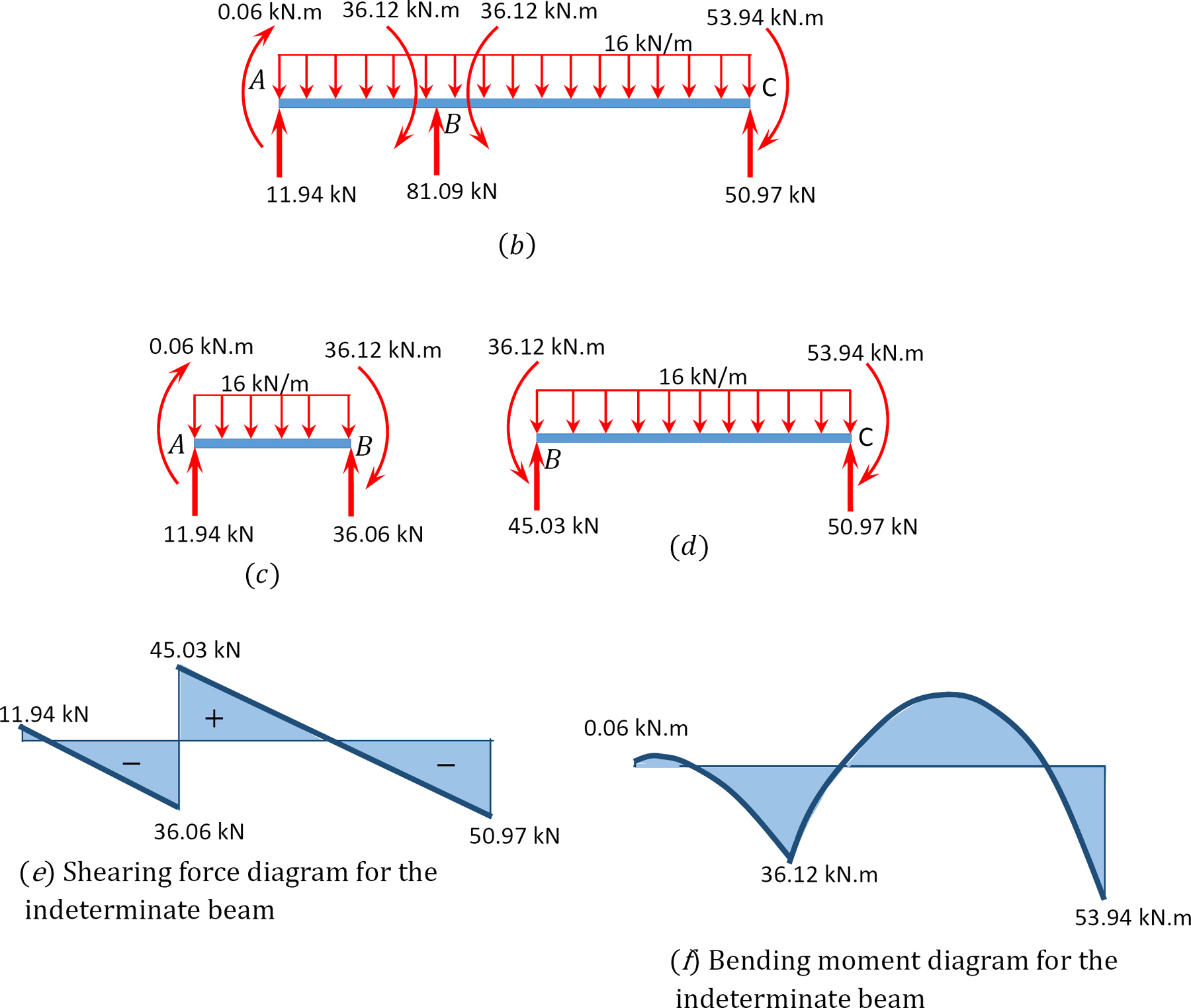
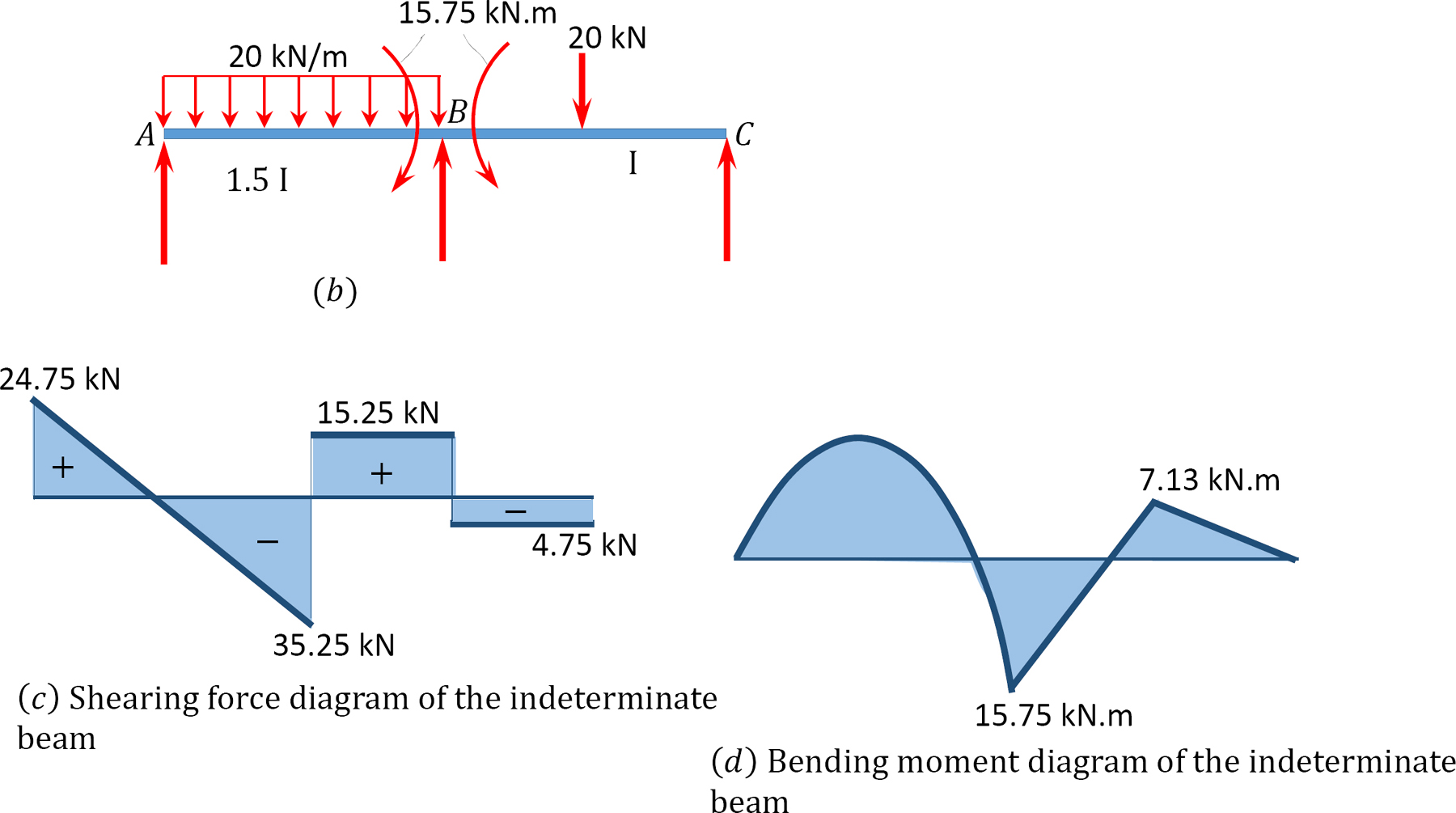
Shear force and bending moment diagrams.
Example 12.2
Using the moment distribution method, determine the end moments and the reactions at the supports of the beam shown in Figure 12.7a. Draw the shearing force and the bending moment diagrams.
Solution
Fixed end moment.
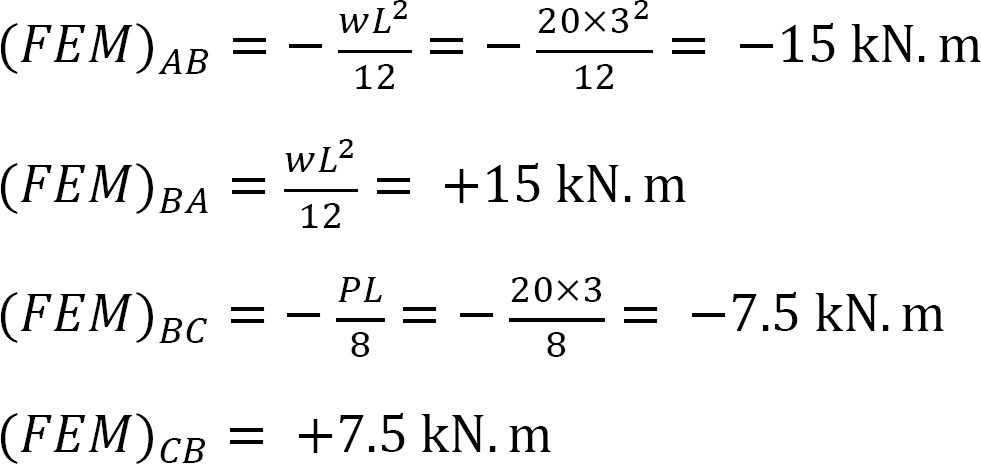
Stiffness factor.
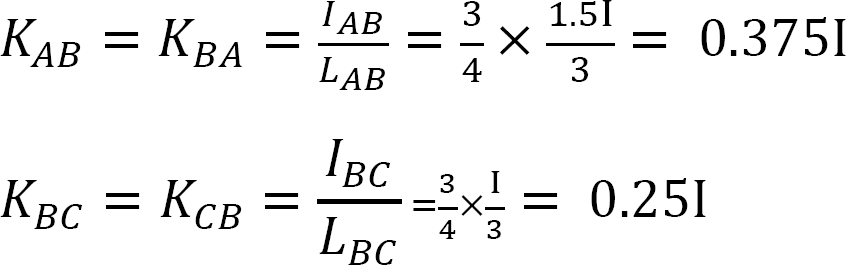
Distribution factor.
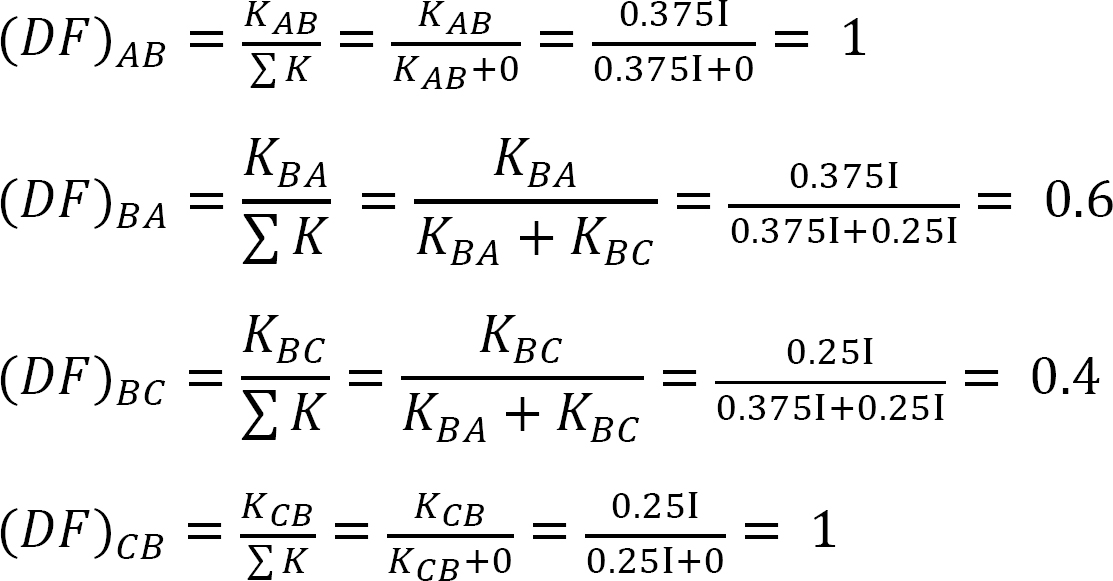
Table 12.2. Distribution table.
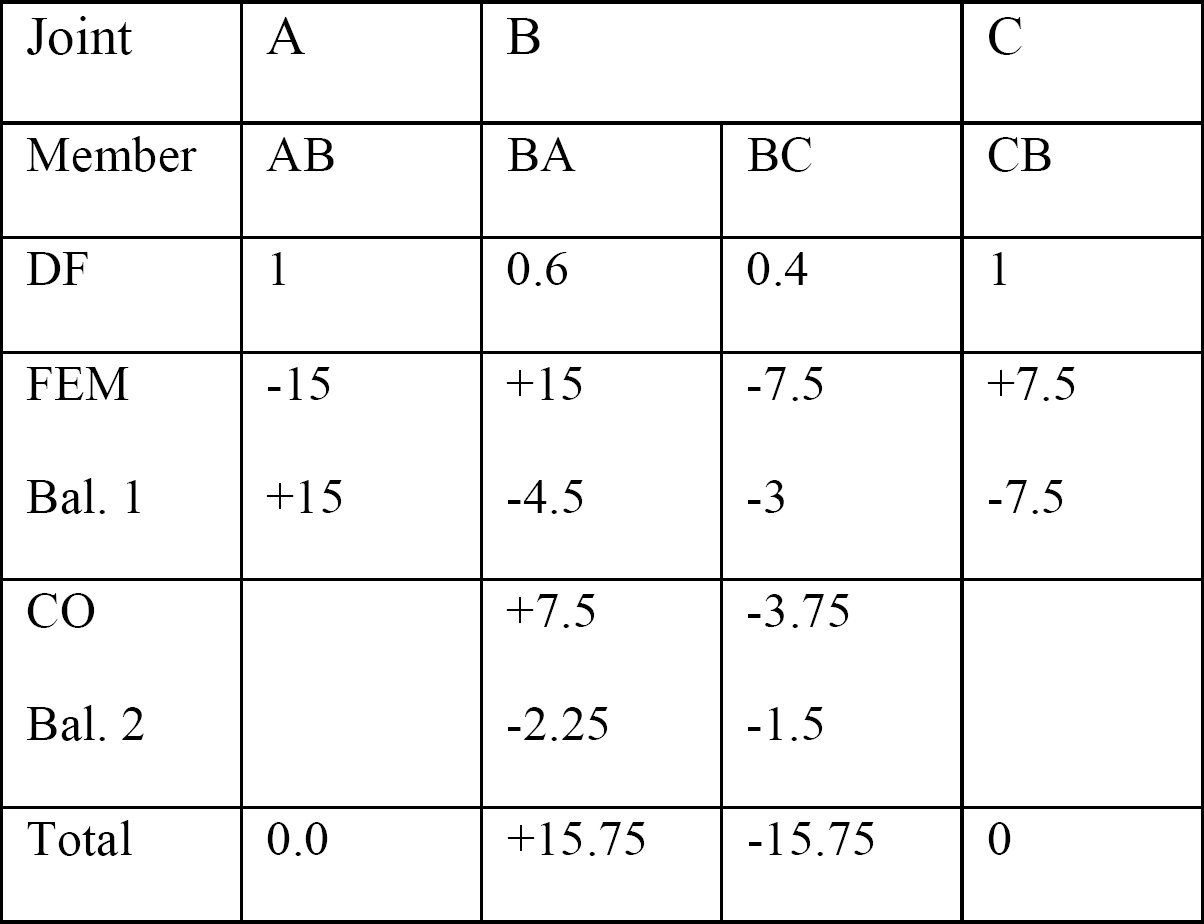
Shear force and bending moment diagrams.
12.6 Analysis of Indeterminate Frames
The procedure for the analysis of frames using the moment distribution method depends on the type of frame that is being analyzed. Frames are categorized as sway- or non-sway frames. The procedure for the analysis of non-sway frames are similar to that of indeterminate beams. But for the analysis of sway frames, the procedure is different. There are two stages involved in the analysis of sway frames, namely the non-sway stage and sway-stage analyses. These stages are described below.
Procedure for Analysis of Indeterminate Sway-Frames by the Moment Distribution Method
A. Non-sway stage analysis
•First assume the existence of an imaginary prop that prevents the frame from swaying.
•Compute the horizontal reactions at the supports of the frame and note the difference X. This is the force to prevent sway.
B. Sway stage analysis
•Assume arbitrary moments to act on the columns of the frame. The magnitude of these moments will vary from column to column in proportion to 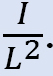
•Values are assumed for M2, and M1 is determined.
•The arbitrary moments are then distributed as for the non-sway condition
•Calculate the magnitude of the horizontal reactions at the supports for the sway condition. The summation of these reactions gives the arbitrary displacing force Y.
•Determine the ratio 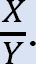 This ratio is called the sway factor.
This ratio is called the sway factor.
•Use the sway factor to multiply the distributed moments of the sway. This gives the corrected moment for the sway.
•The final moments for the frame are the summation of the moments obtained in the non-sway stage and the corrected moment for the sway stage.
Example 12.3
Using the moment distribution method, determine the members’ end moments of the frame shown in Figure 12.8. EI = constant.
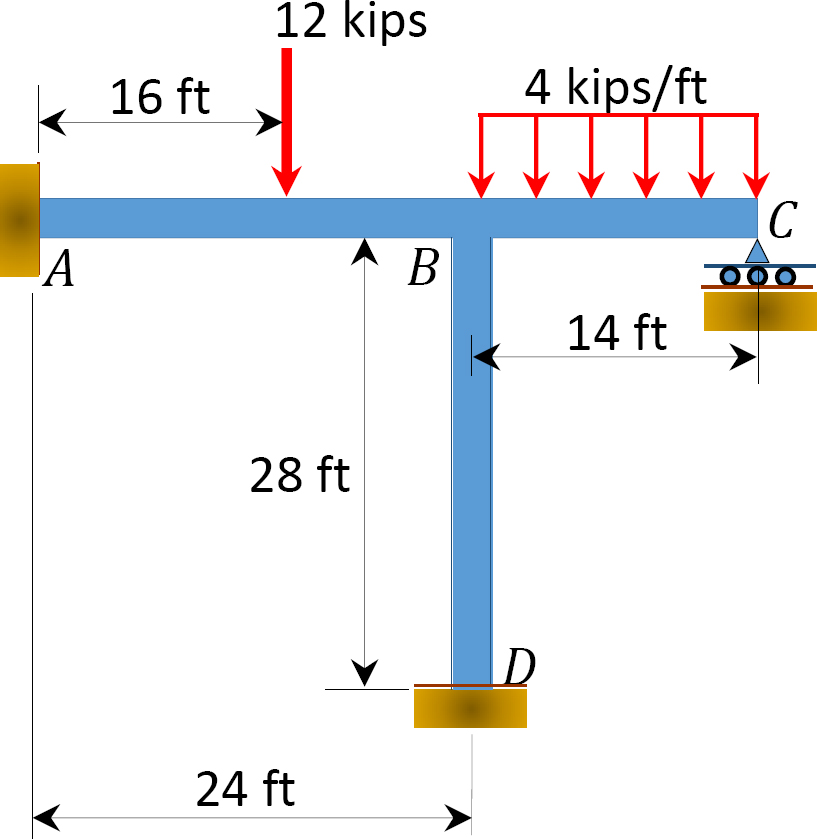
Solution
Fixed end moment.
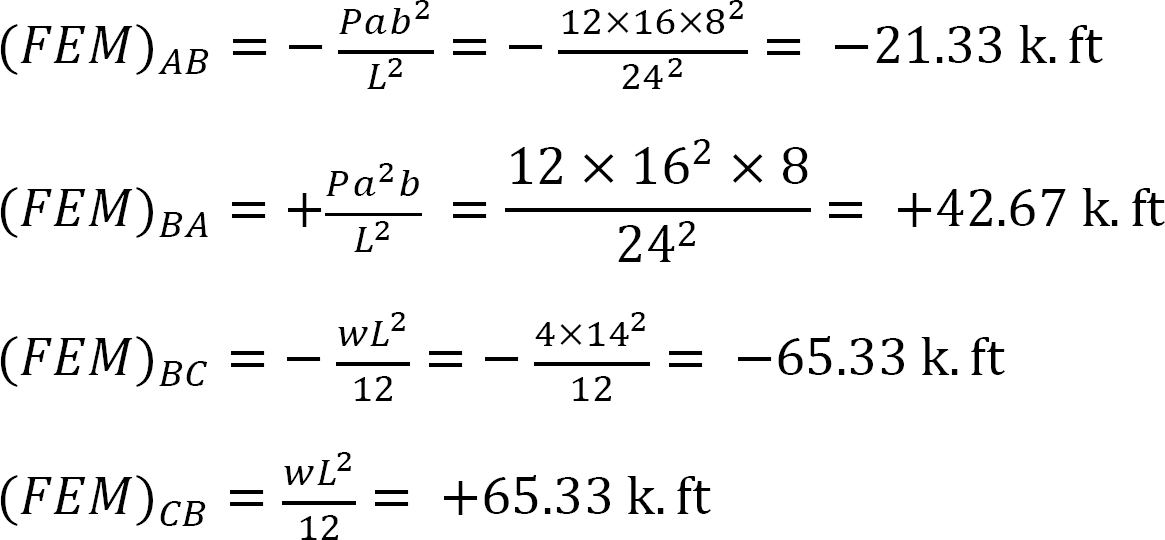
Stiffness factor.
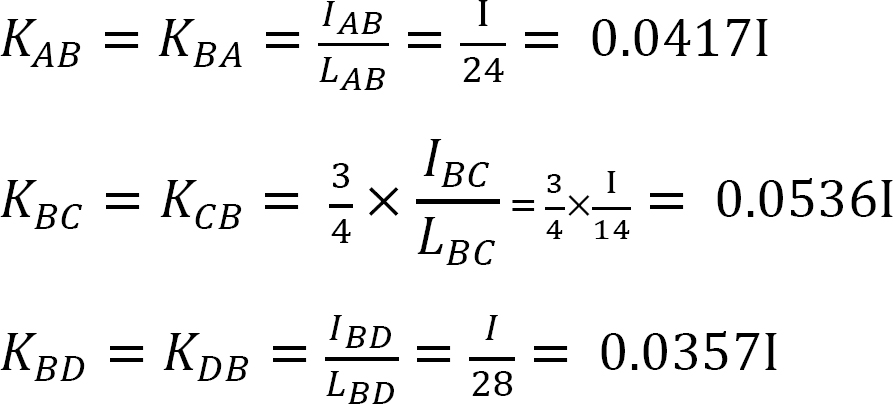
Distribution factor.
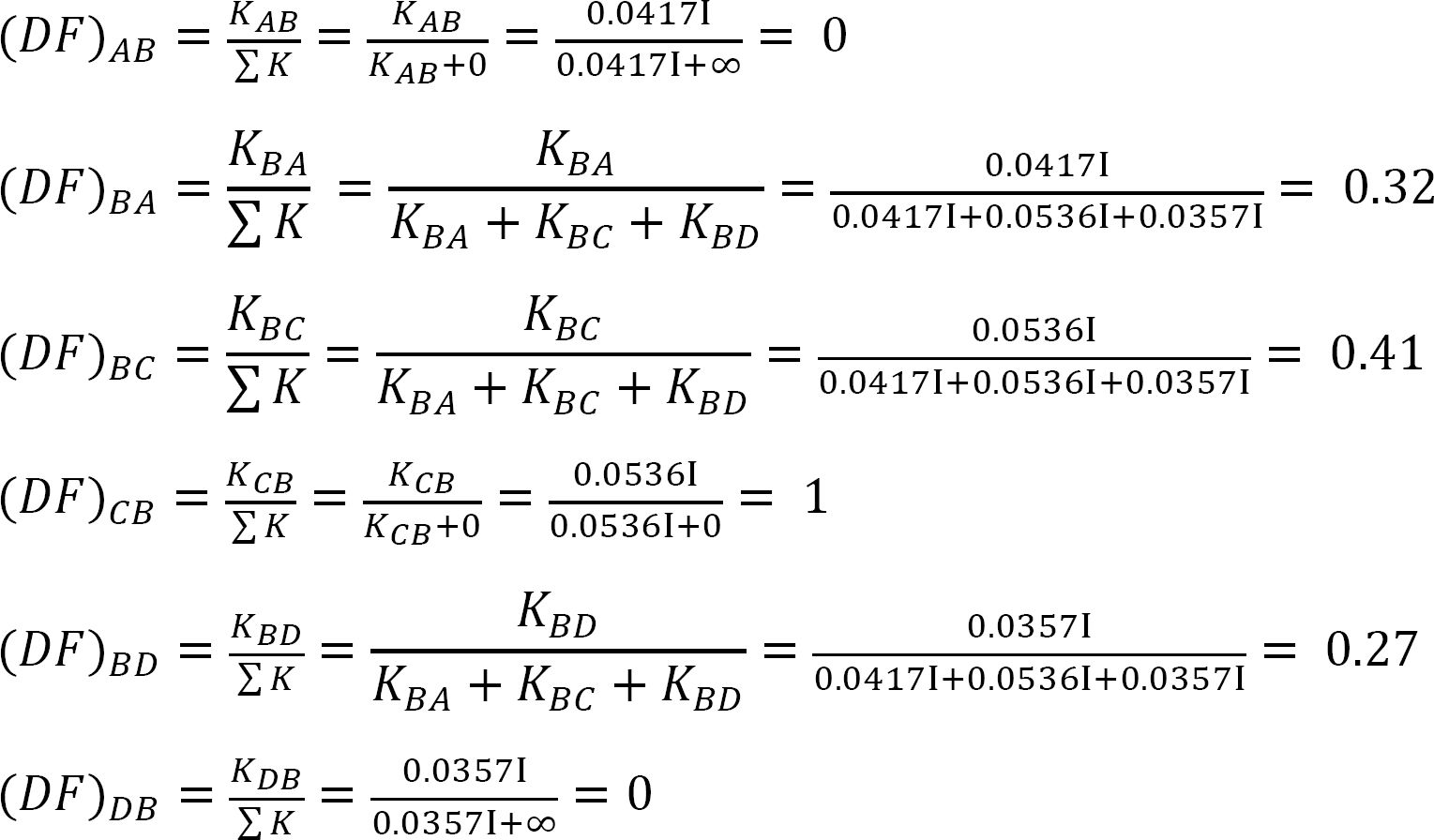
Table 12.3. Distribution table.
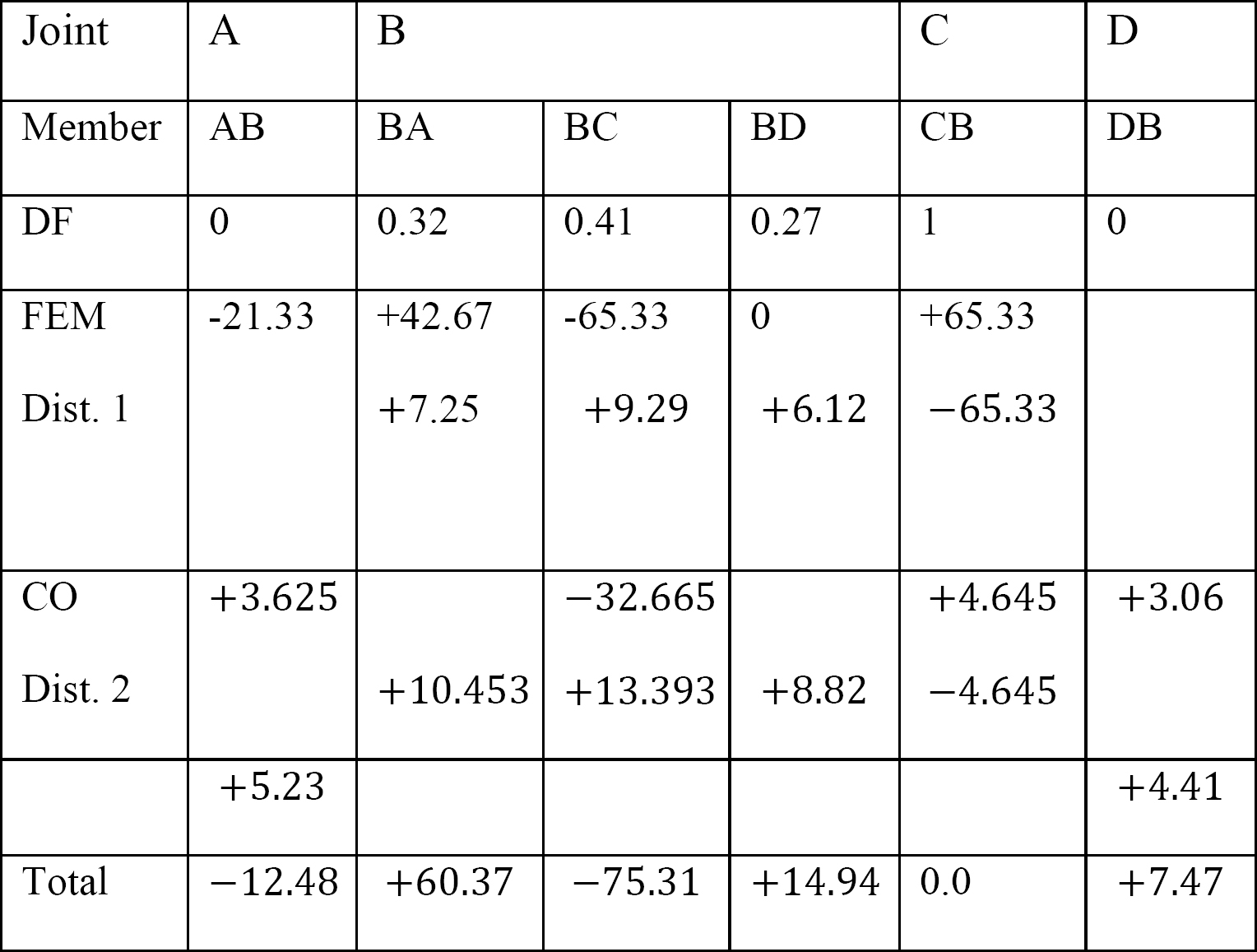
Final member end moments.
Substituting the obtained values of EKθB, EKθC, and EK∆ into the member end moment equations suggests the following:
MAB = –12.48 k. ft
MBA = +60.37 k. ft
MBC = –75.31 k. ft
MBD = +14.94 k. ft
MCB = 0
MDB = +7.47 k. ft
Example 12.4
Using the moment distribution method, determine the end moments at the supports of the frame shown in Figure 12.9. EI = constant.
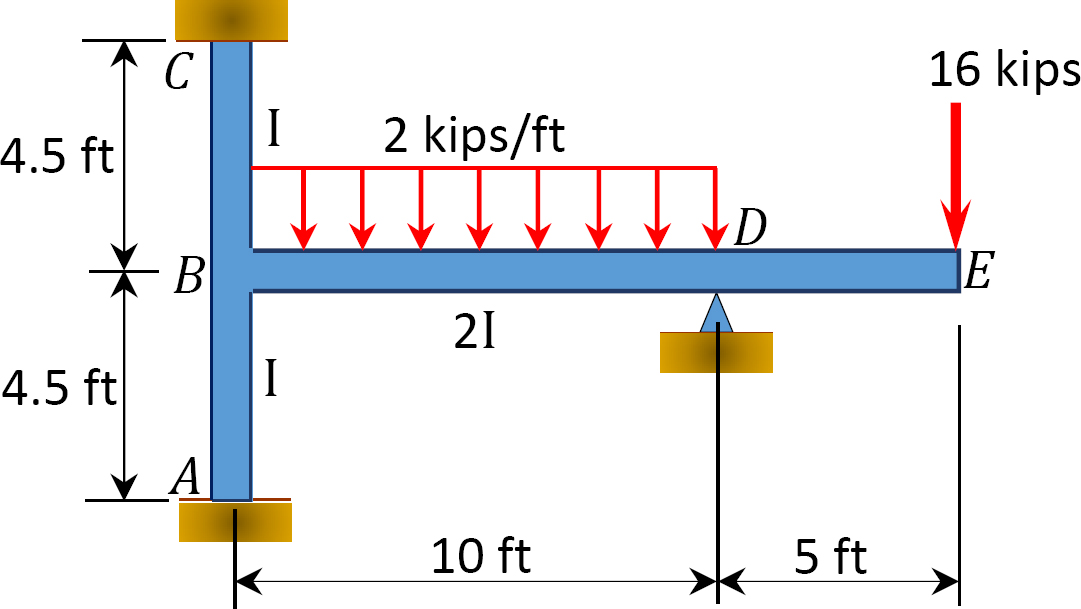
Solution
Fixed end moment.
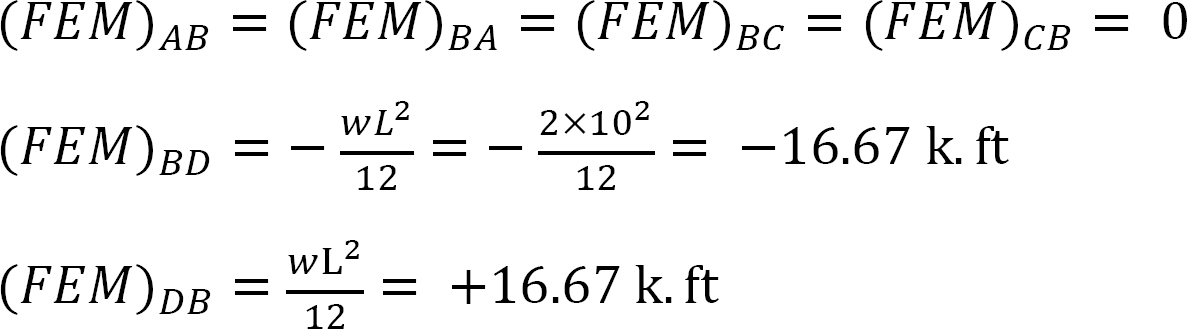
Stiffness factor.
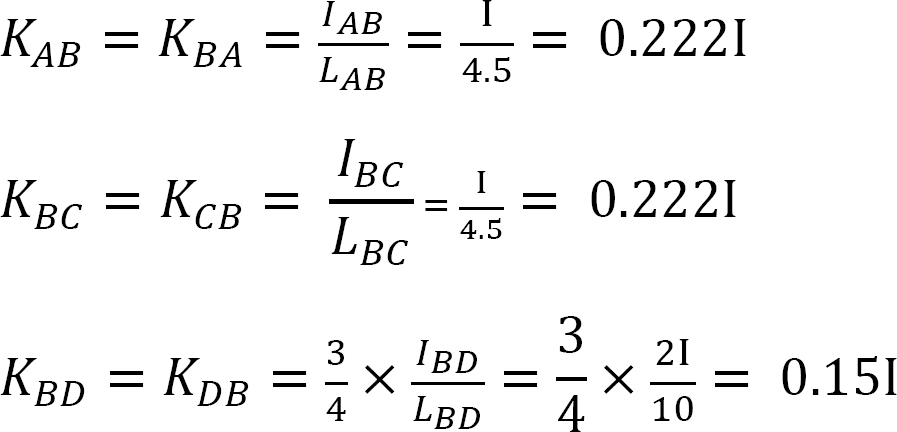
Distribution factor.

Table 12.4. Distribution table.
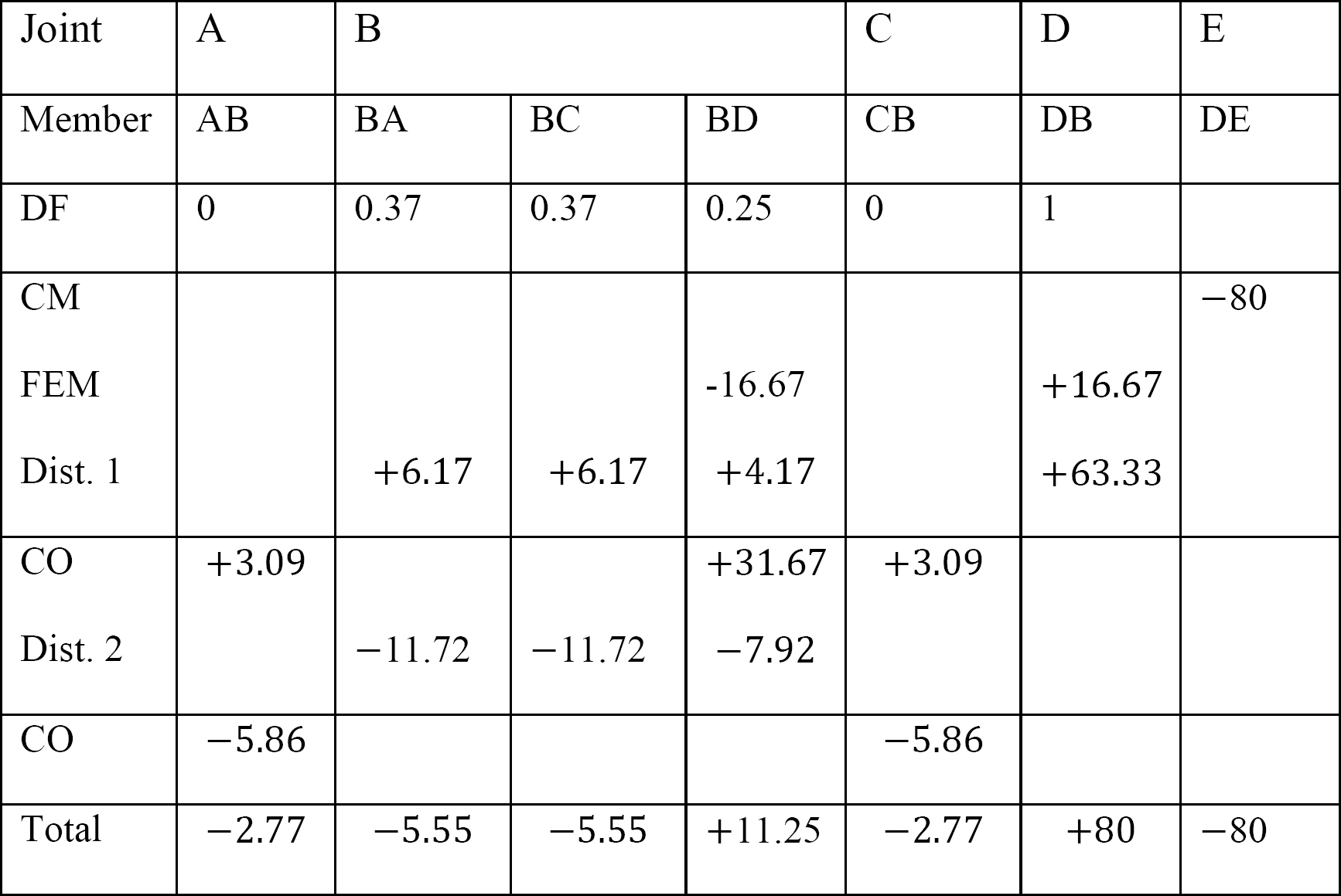
Final member end moments.
MAB = –2.77 k. ft
MBA = –5.55 k. ft
MBC = –5.55 k. ft
MBD = +11.25 k. ft
MCB = –2.77
MDB = +80 k. ft
MDE = –80 k. ft
Example 12.5
Using the moment distribution method, determine the end moments at the supports of the frame shown in Figure 12.10. EI = constant.
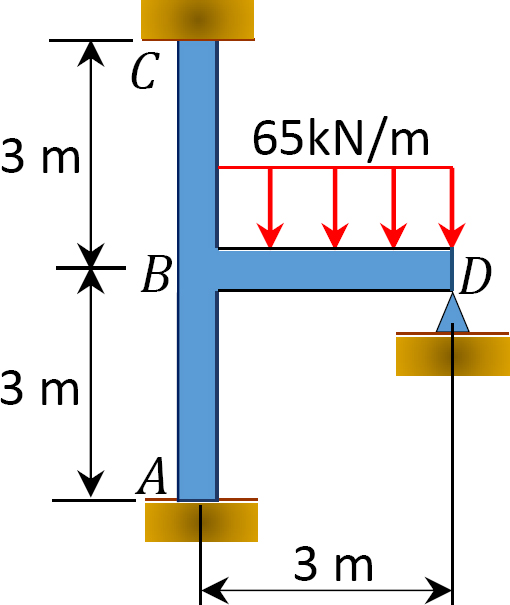
Solution
Fixed end moment.
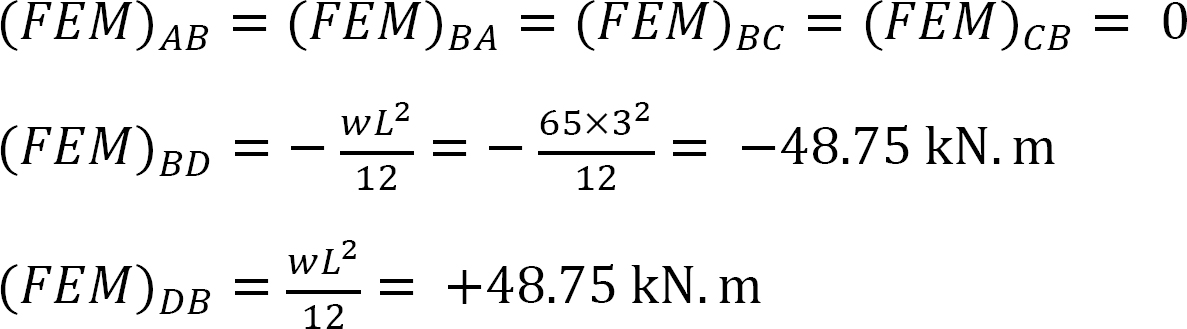
Stiffness factor.
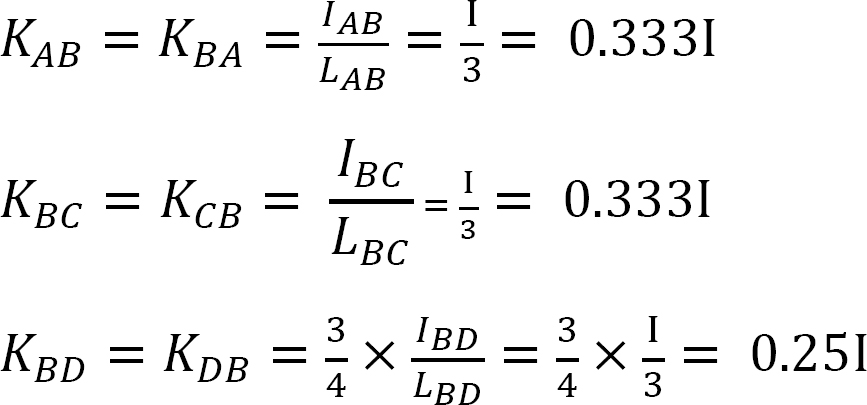
Distribution factor.
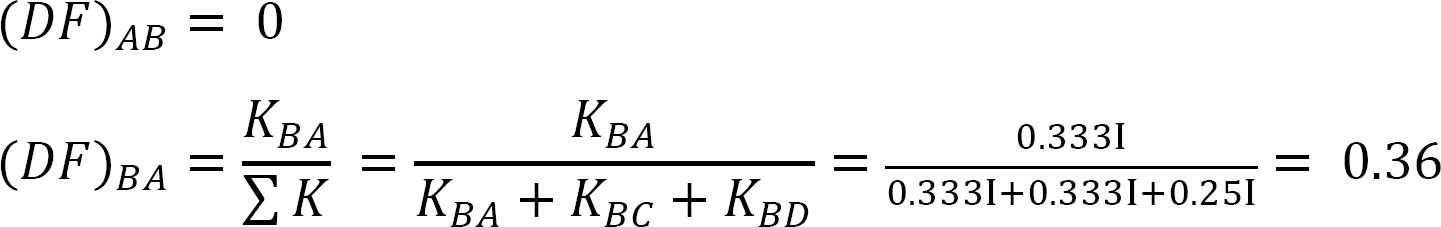

Table 12.5. Distribution table.
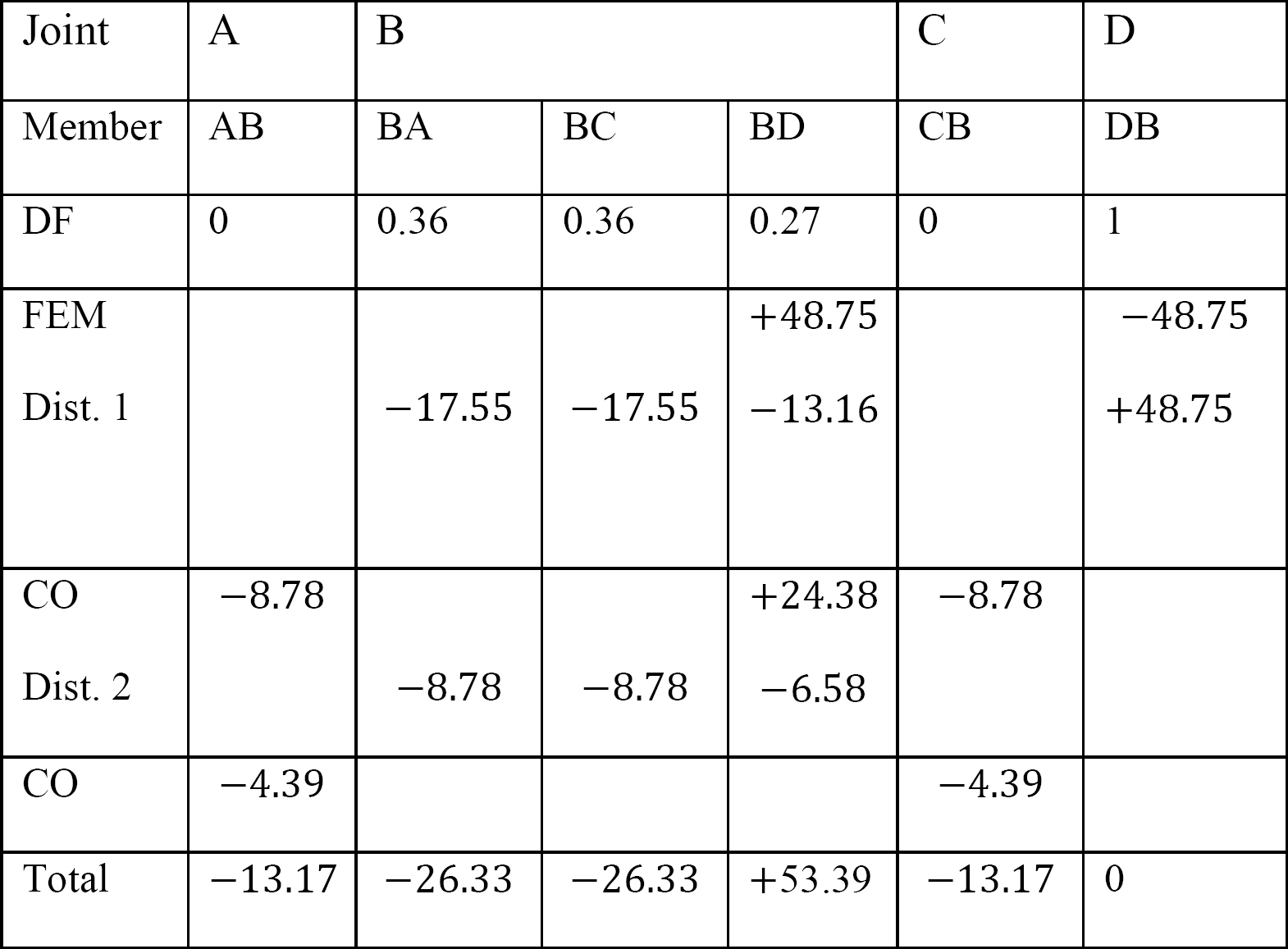
Final member end moments.
MAB = –13.17 k. ft
MBA = –26.33 k. ft
MBC = –26.33 k. ft
MBD = +53.39 k. ft
MCB = –13.17 k. ft
MDB = 0
Example 12.6
Using the moment distribution method, determine the member end-moments of the frame with side-sway shown in Figure 12.11a.
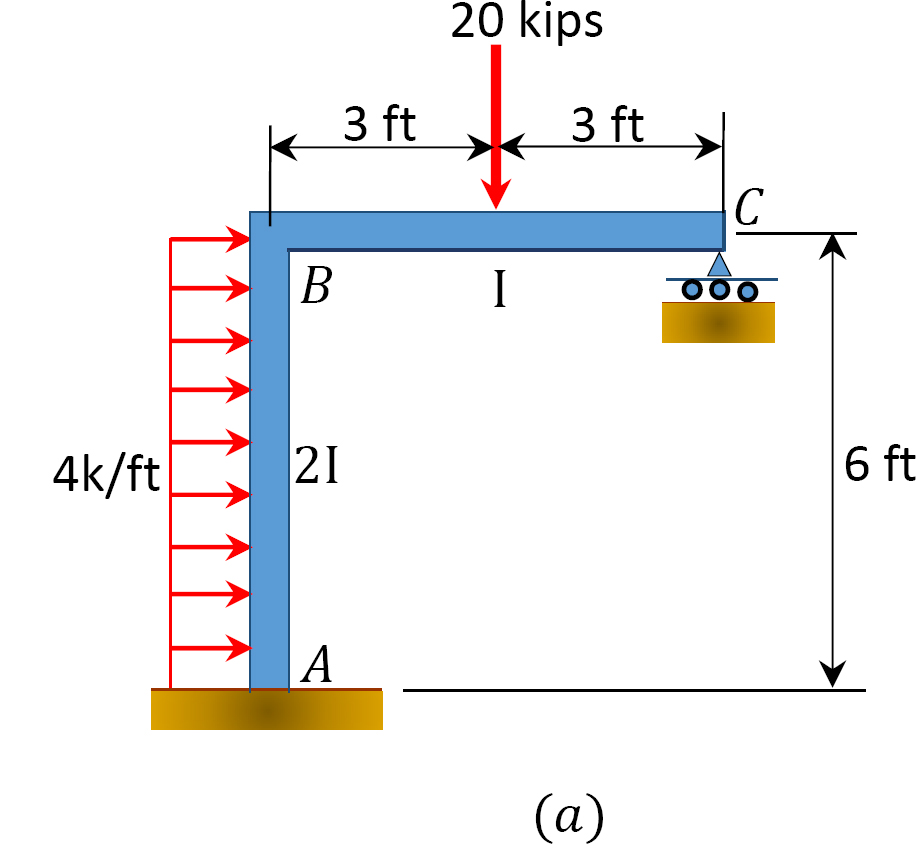
Solution
Fixed end moment.
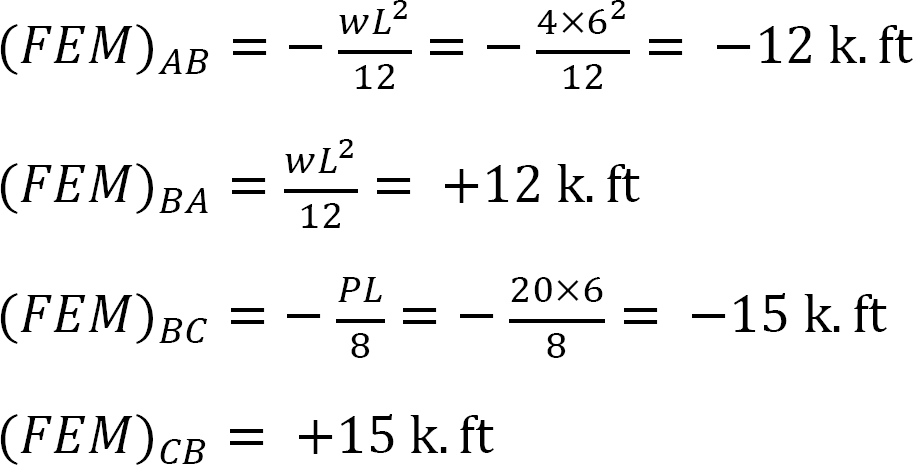
Stiffness factor.
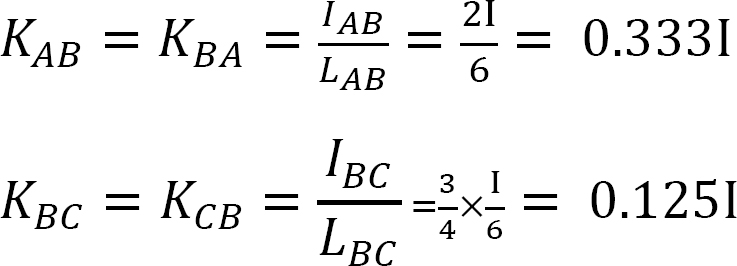
Distribution factor.
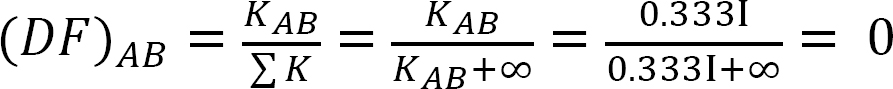

Analysis of frame without side-sway.
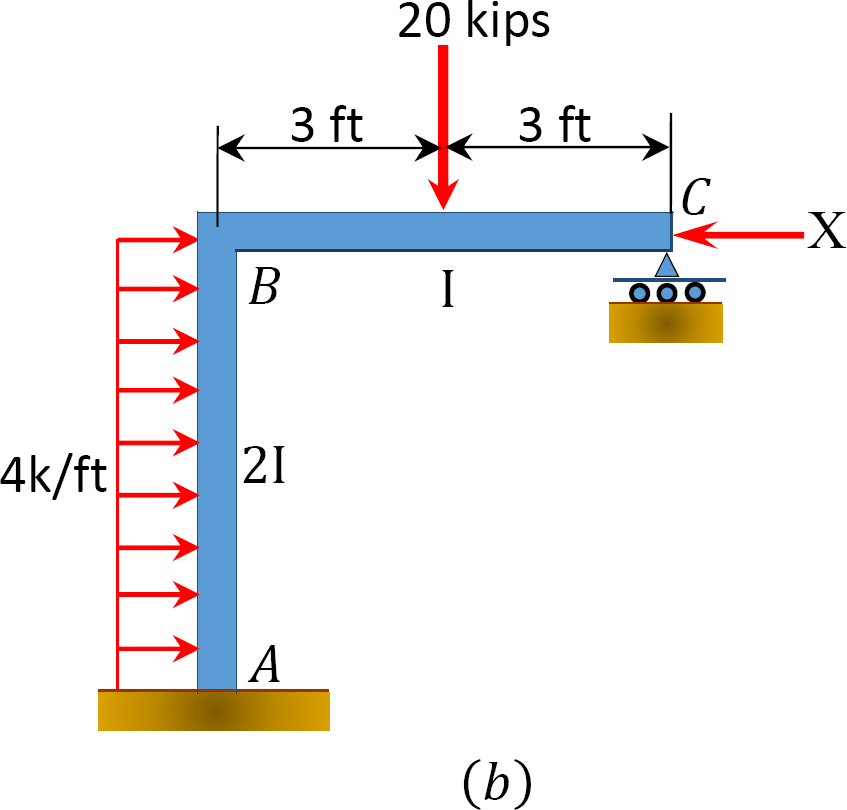
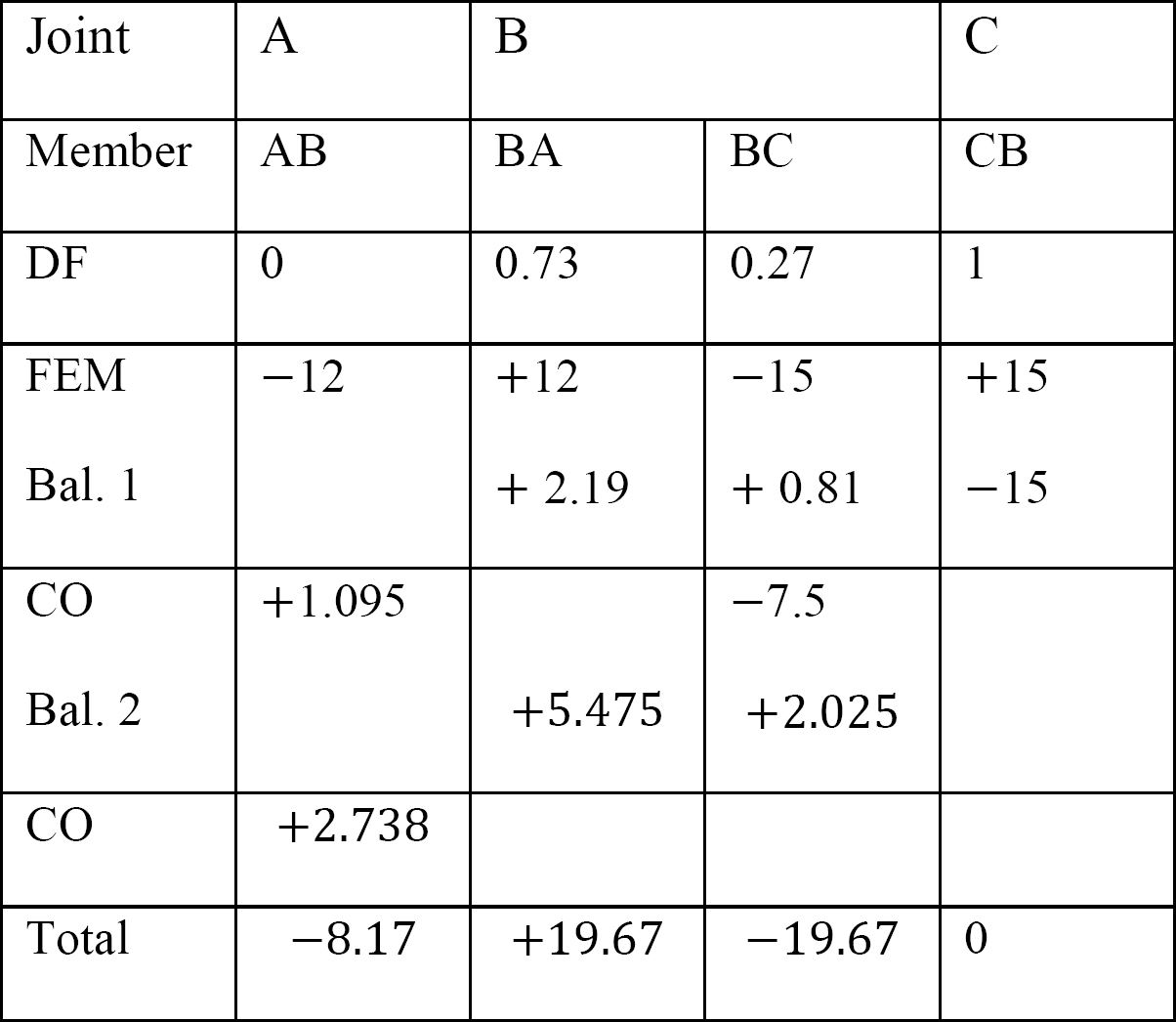
Table 12.6. Distribution table (no sway frame).
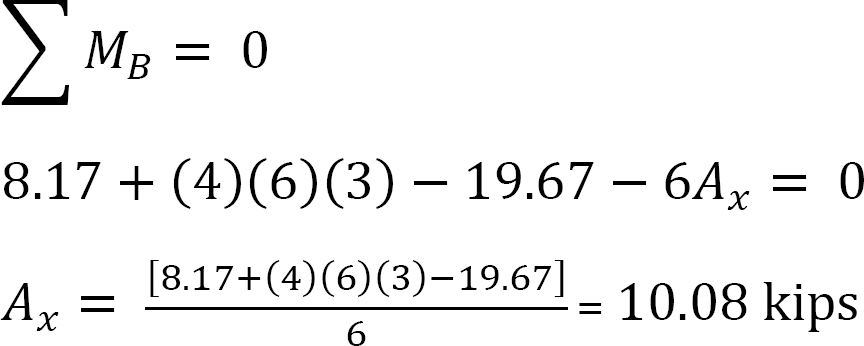
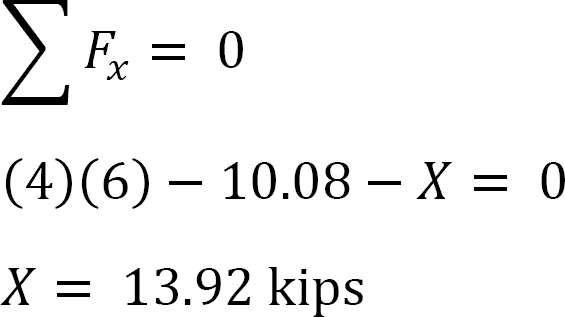
Analysis of frame with side-sway.
Assume that MAB = +20 k. ft
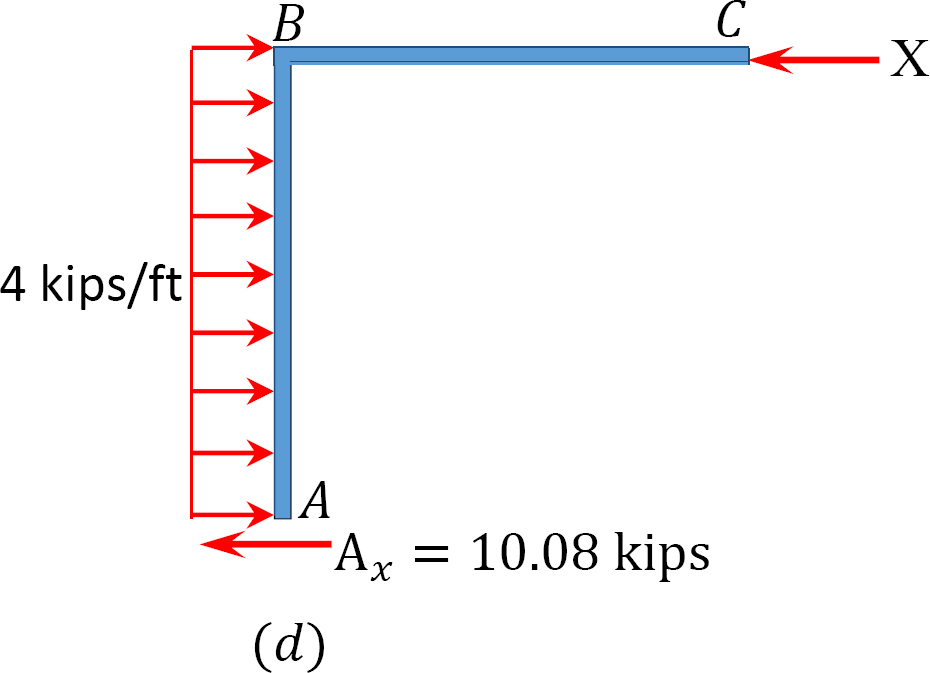
Table 12.7. Distribution table (sway frame).
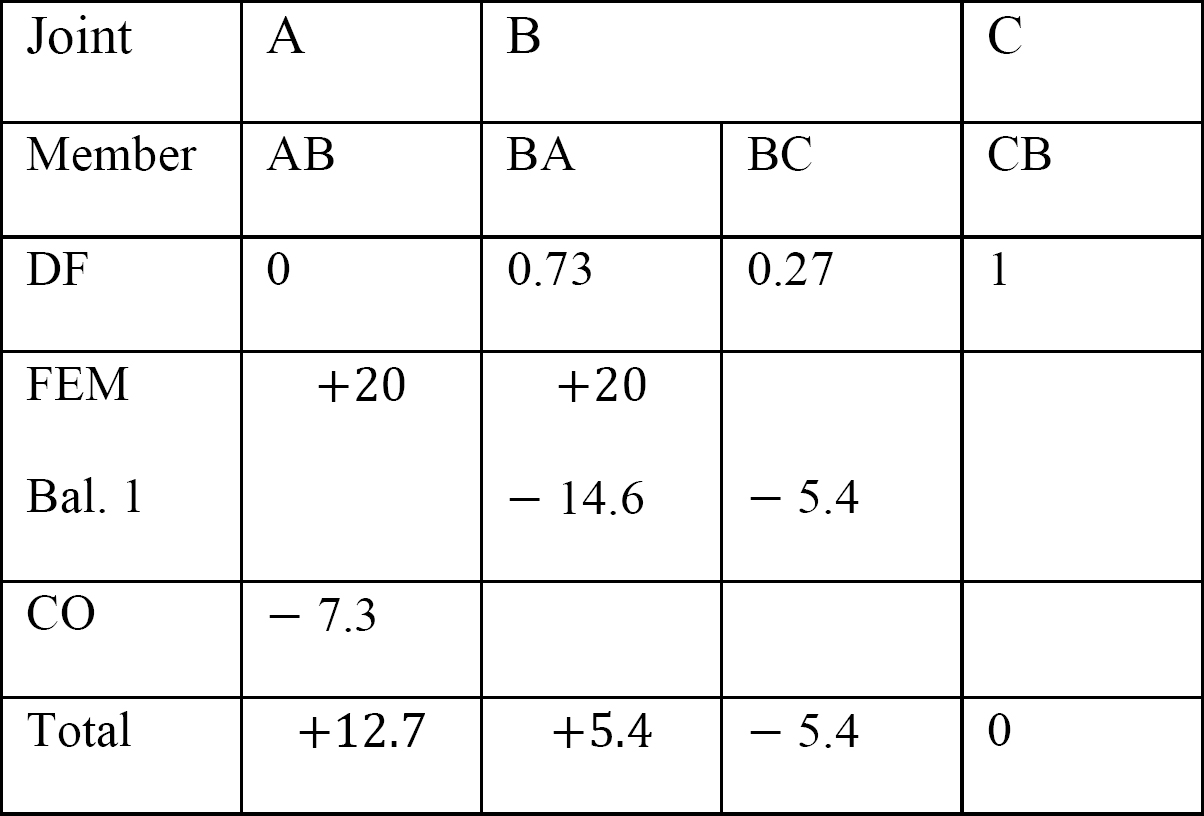
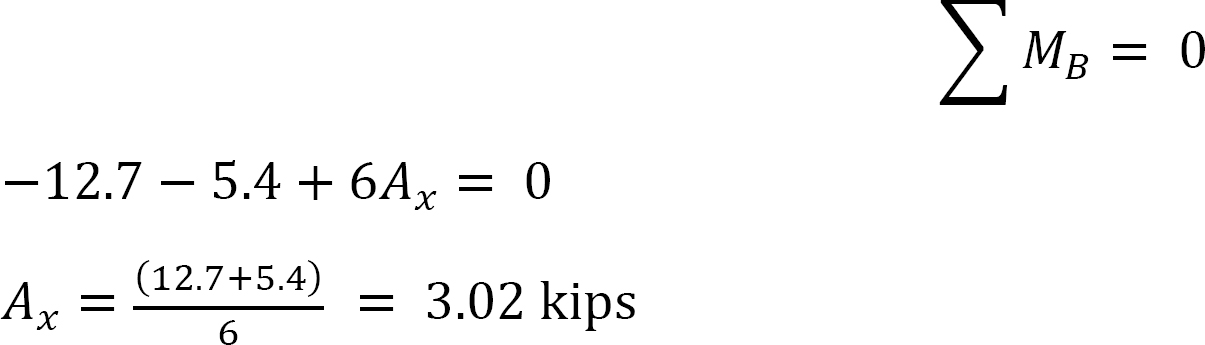
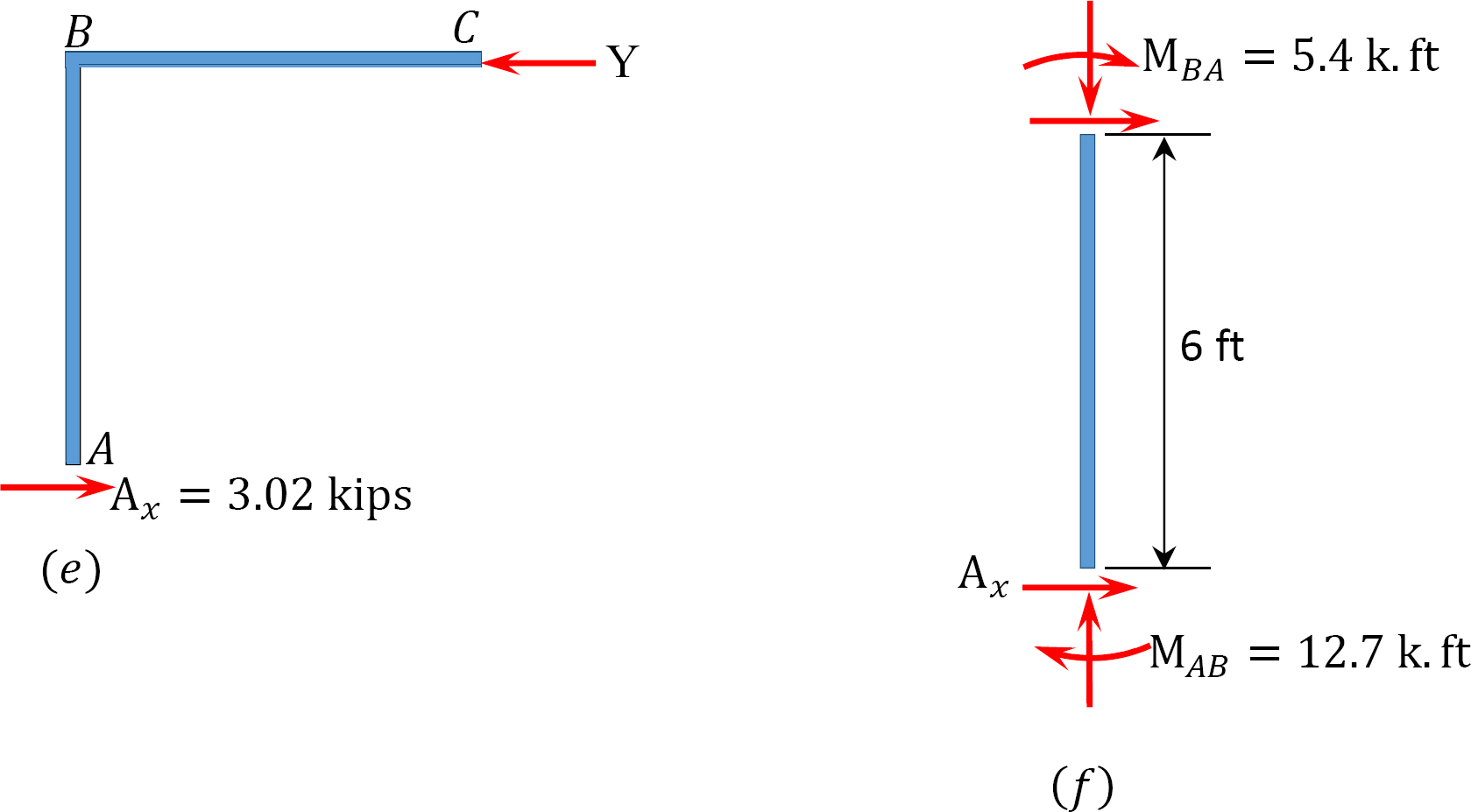
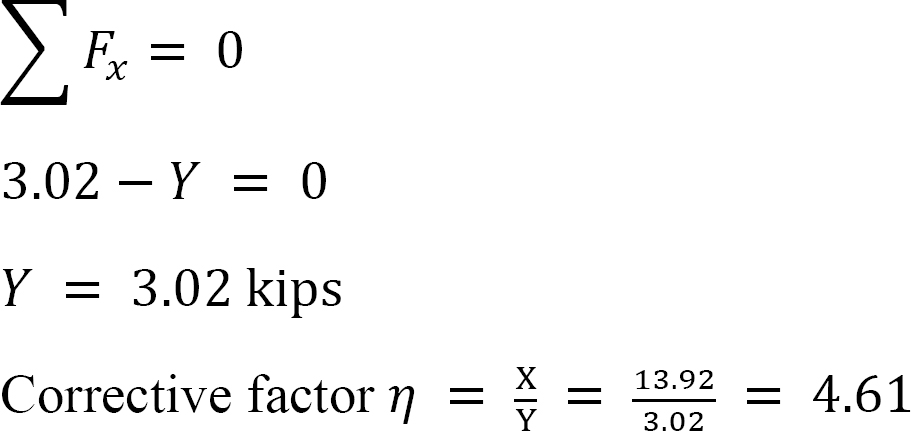
Final end moments.
Example 12.7
A sway frame is loaded as shown in Figure 12.12a. Using the moment distribution method, determine the end moments of the members of the frame.
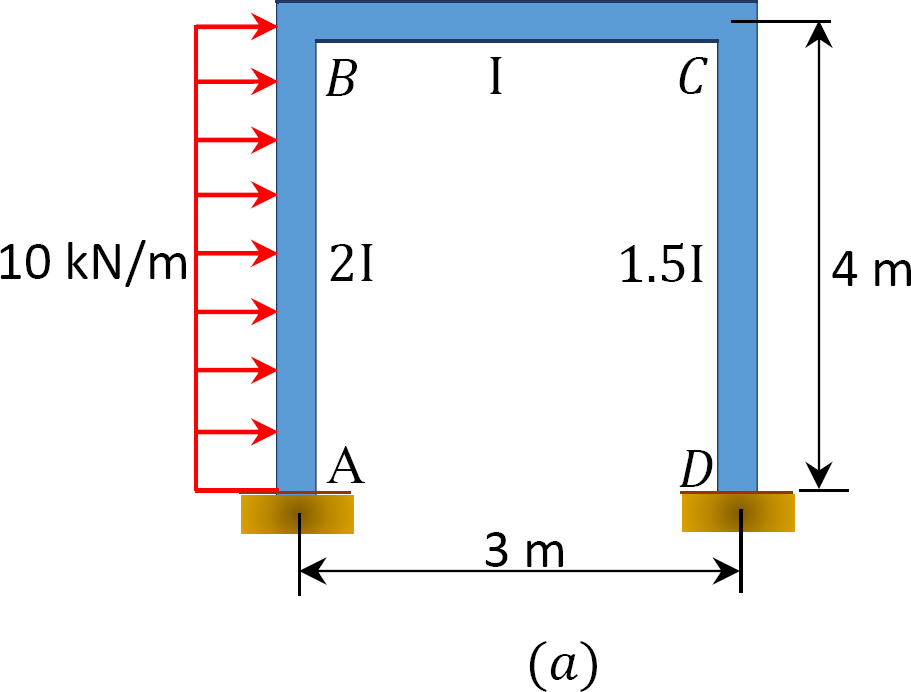
Solution
Fixed end moment.
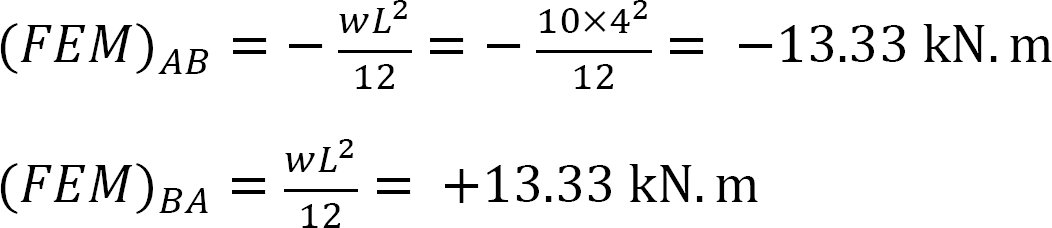
Stiffness factor.
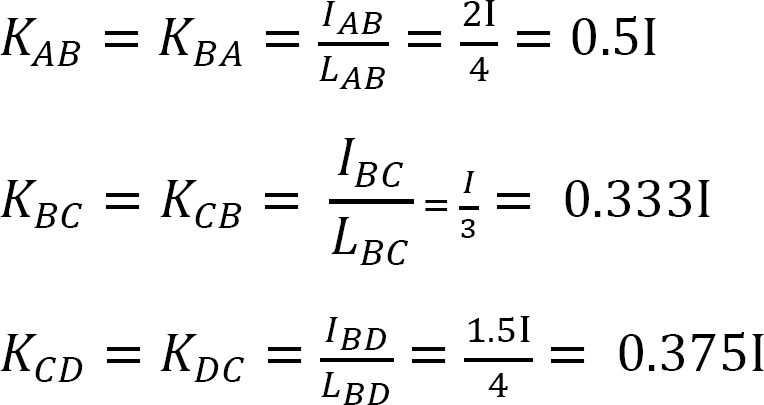
Distribution factor.

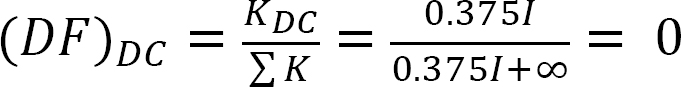
Analysis of frame without side-sway.
Table 12.8. Distribution table (no sway frame).
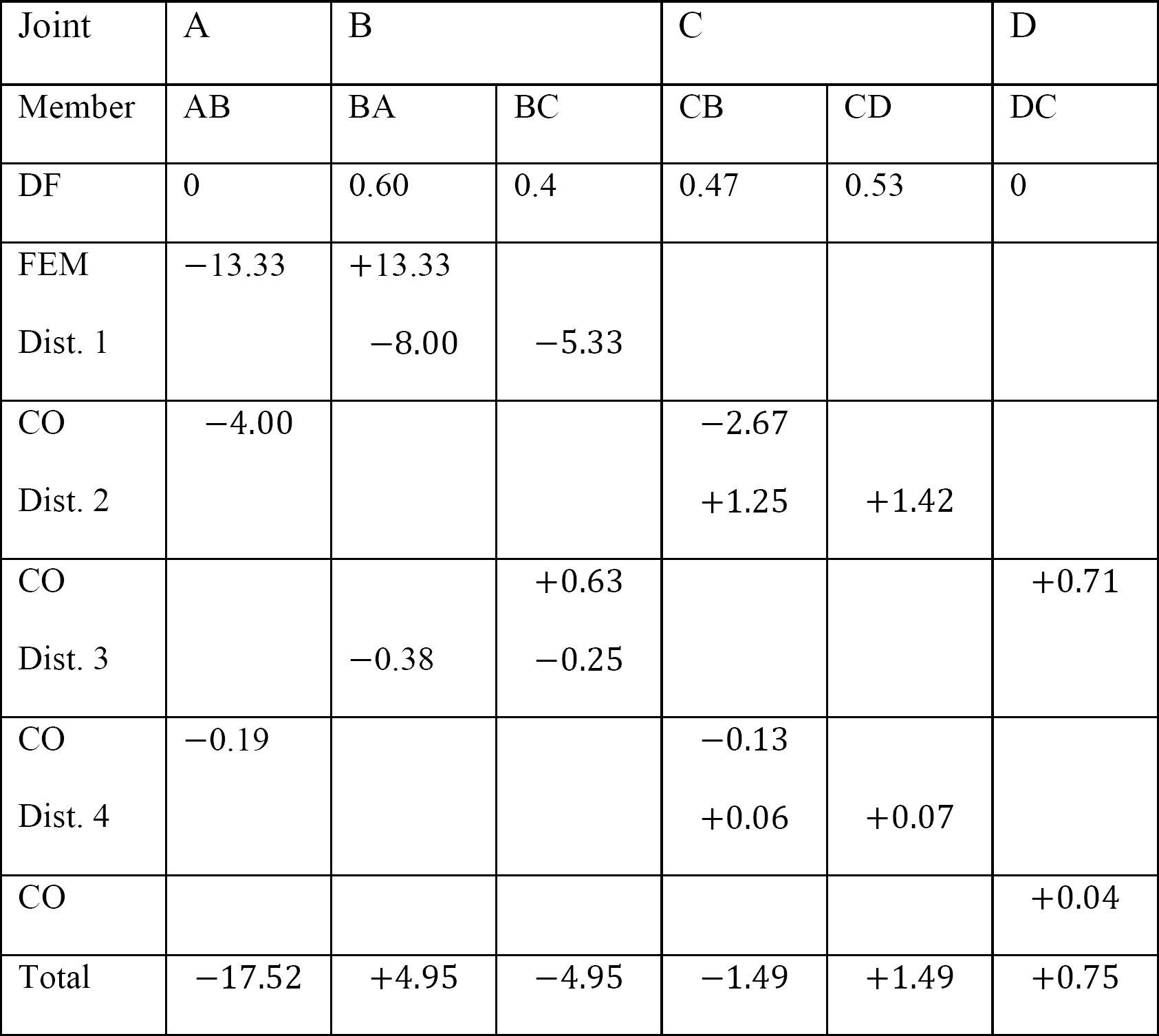
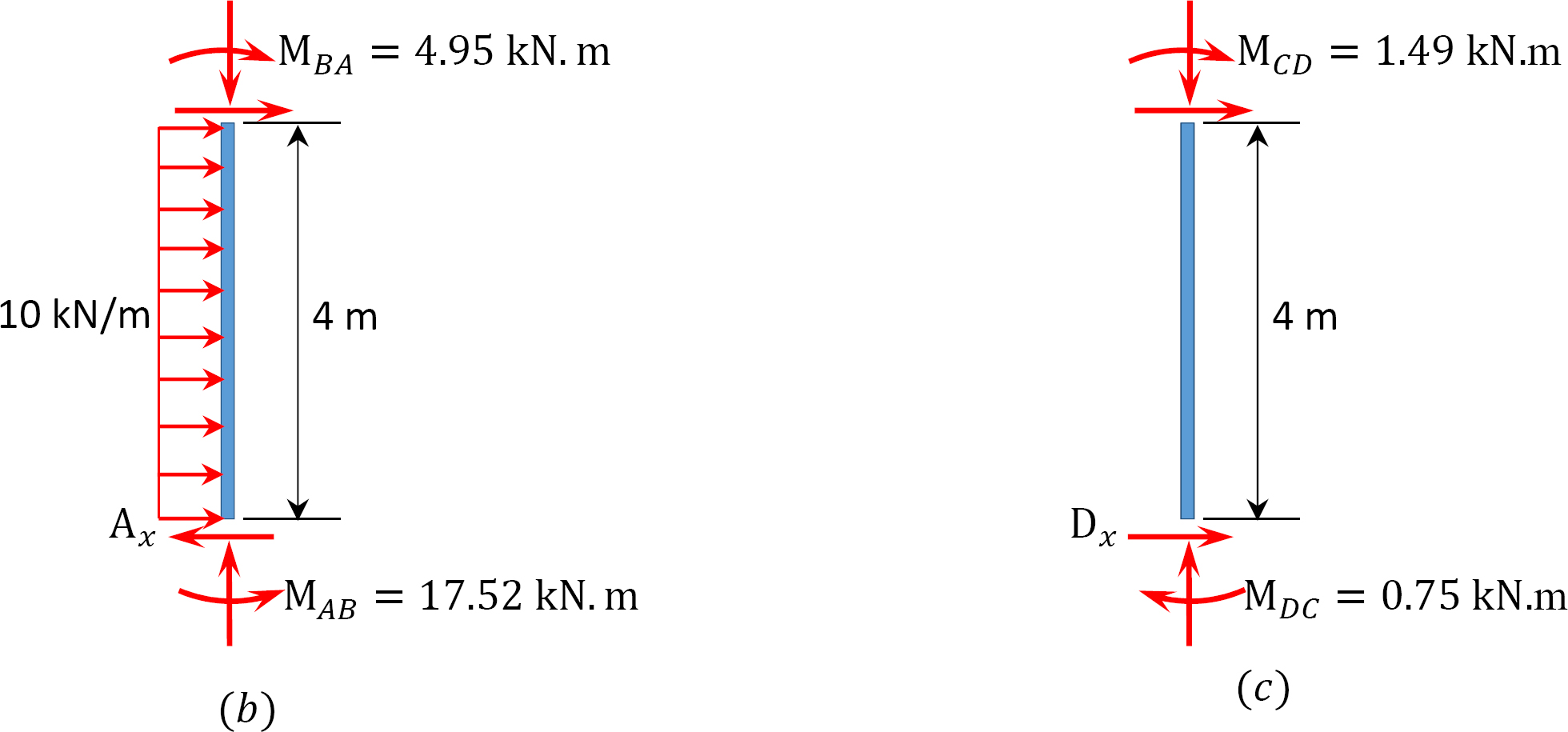
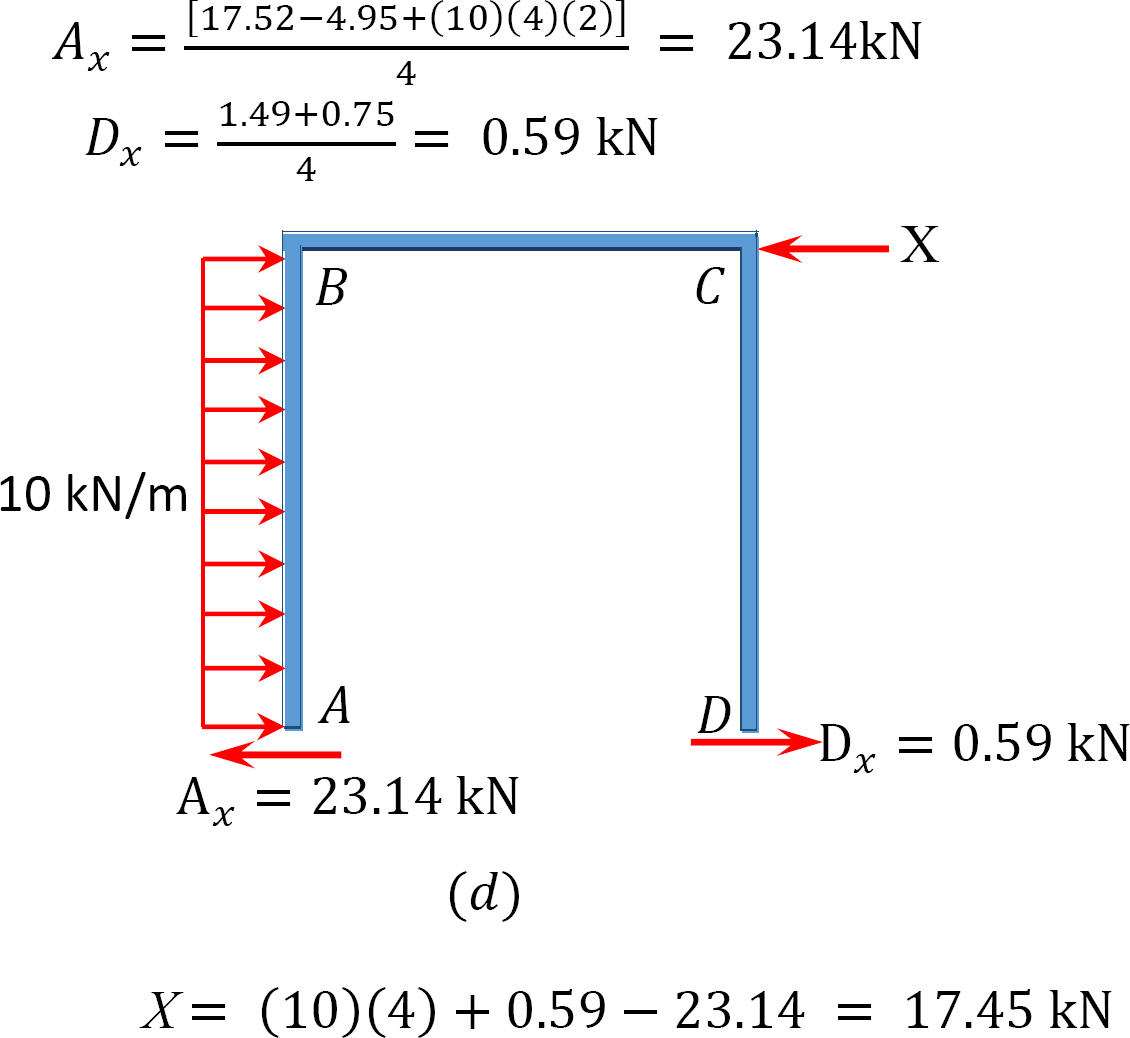
Table 12.9. Distribution table (sway frame).
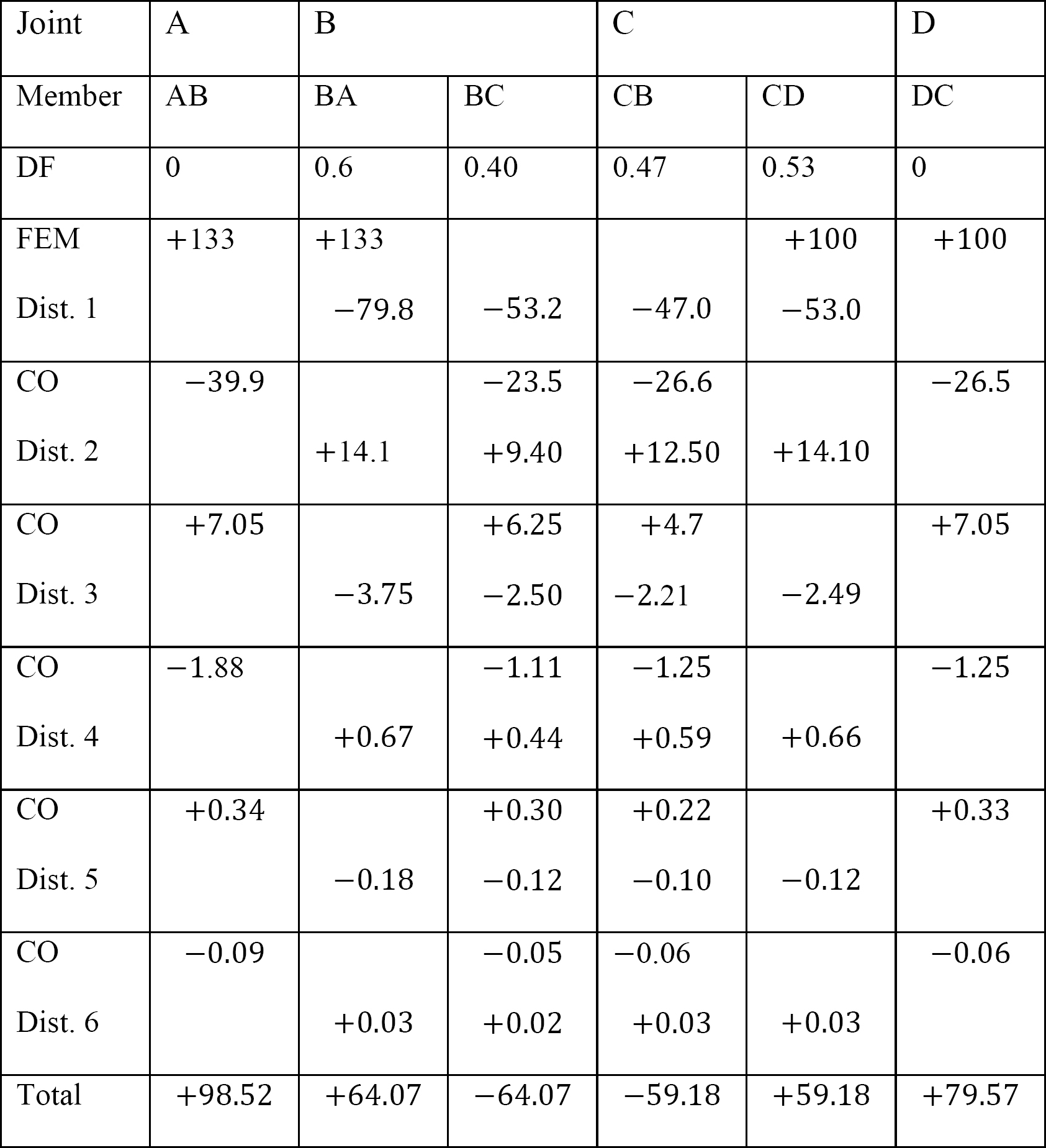
Analysis of frame with side-sway.
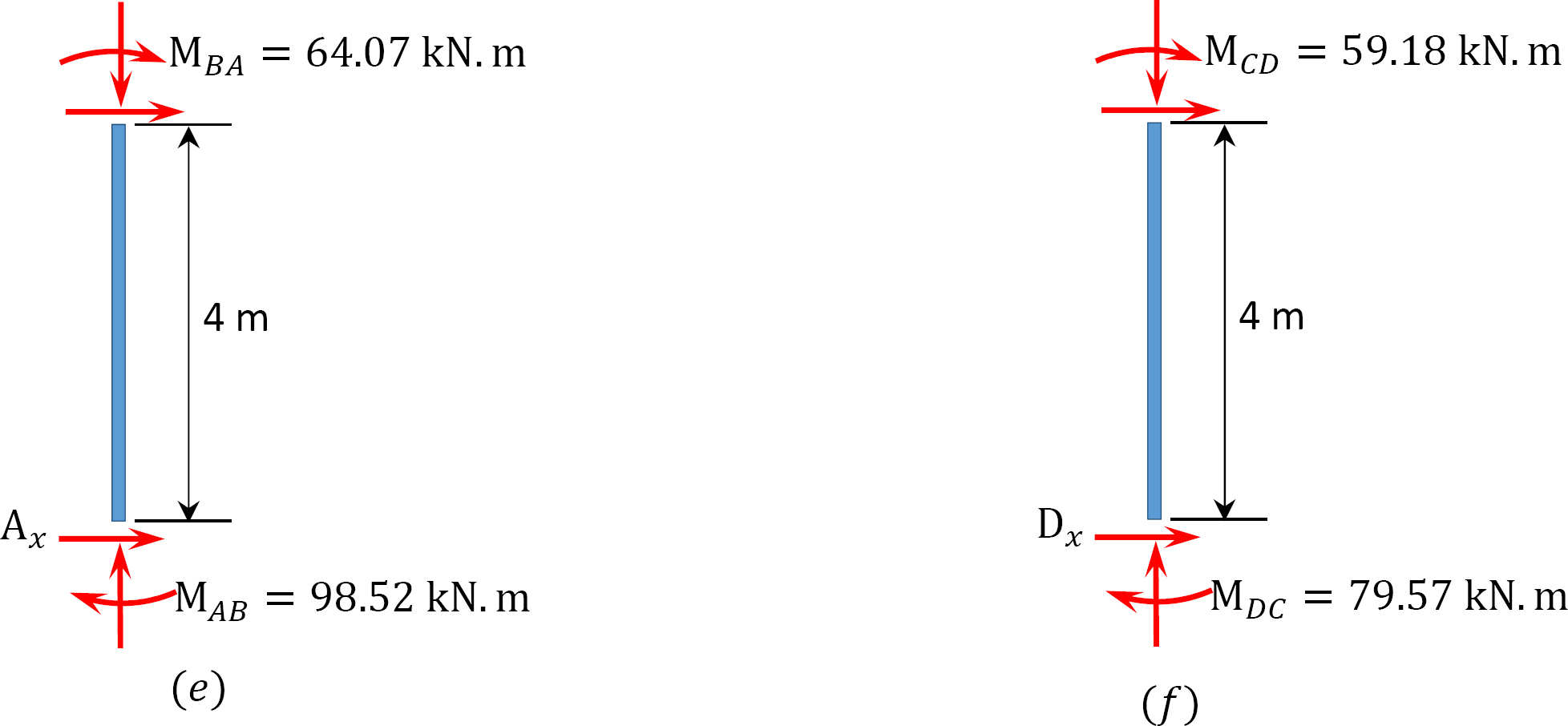
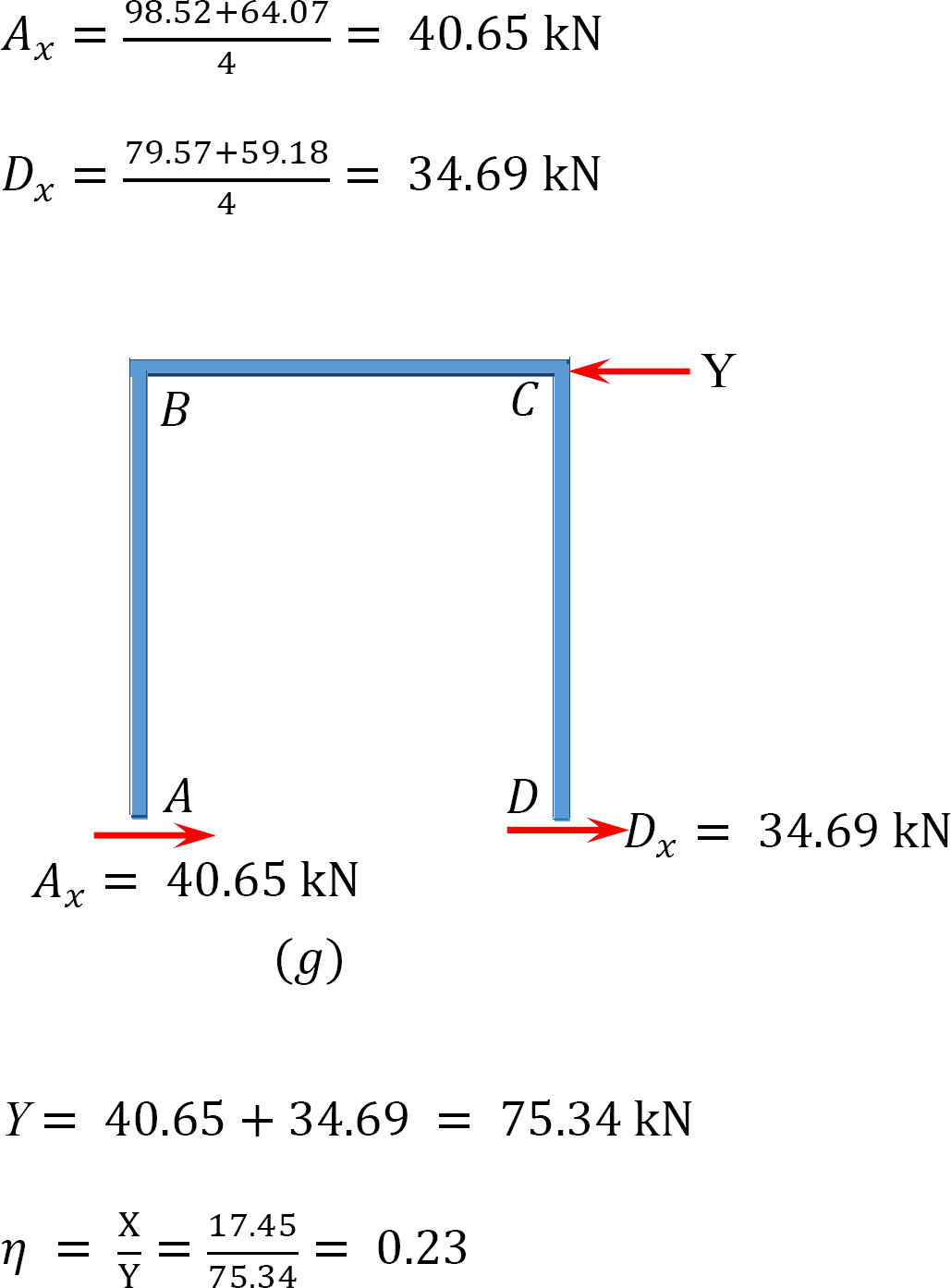
Final end moment.
MAB = –17.52 + (98.52)(0.23) = 5.14 kN. m
MBA = 4.95 + (64.07)(0.23) = 19.69 kN. m
MBC = –4.95 + (–64.07)(0.23) = –19.69 kN. m
MCB = –1.49 + (–59.18)(0.23) = –15.10 kN. m
MCD = 1.49 + (59.18)(0.23) = 15.10 kN. m
MDC = 0.75 + (79.57)(0.23) = 19.05 kN. m
Chapter Summary
Moment distribution method of analysis of indeterminate structures: The moment distribution method of analysis is an approximate method of analysis. Its degree of accuracy is dependent on the number of iterations. In this method, it is assumed that all joints in a structure are temporarily locked or clamped and, thus, are prevented from possible rotation. Loads are applied to the members, and the moments developed at the member ends due to fixity are determined. Joints in the structure are then unlocked successively, and the unbalanced moment at each joint is distributed to members meeting at that joint. Carry over moments at members’ far ends are determined, and the process of balancing is continued until the desired level of accuracy. Members’ end moments are determined by adding up the fixed-end moment, the distributed moment, and the carry over moment. Once members’ end moments are determined, the structure becomes determinate.
Practice Problems
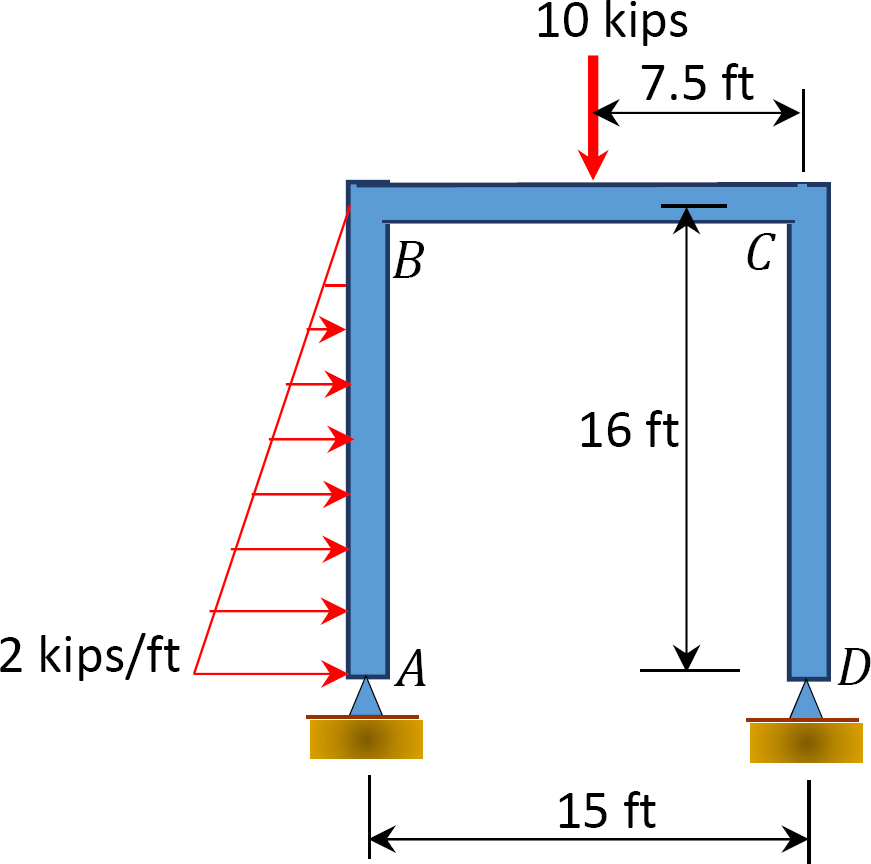
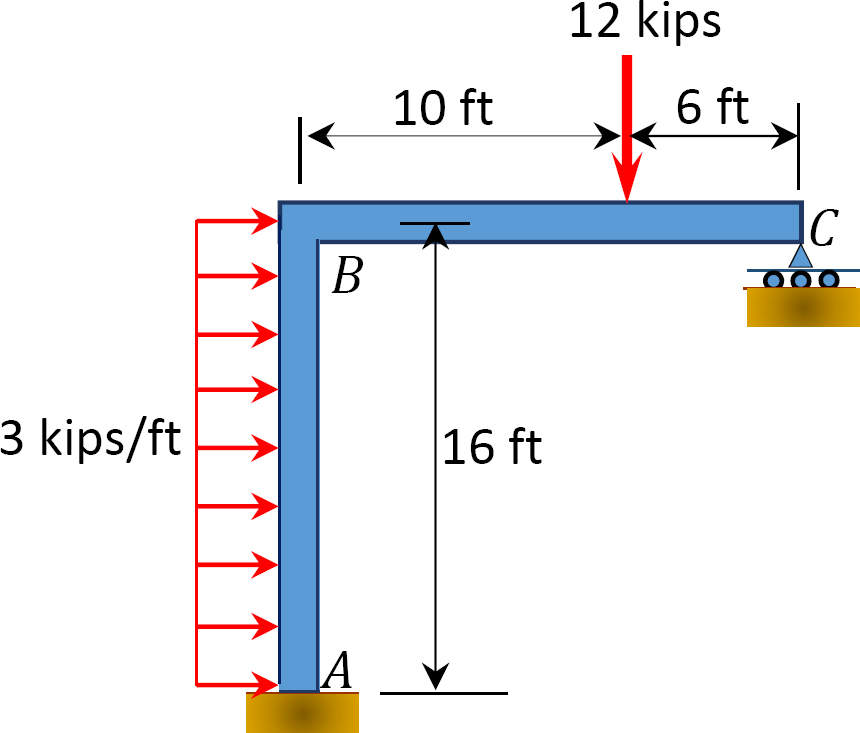
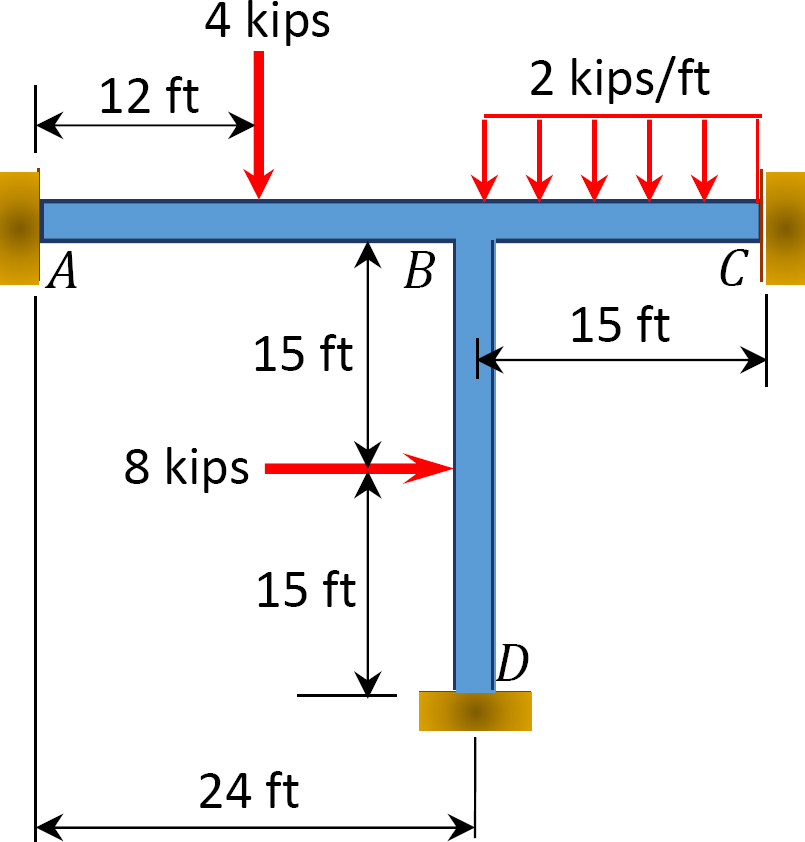
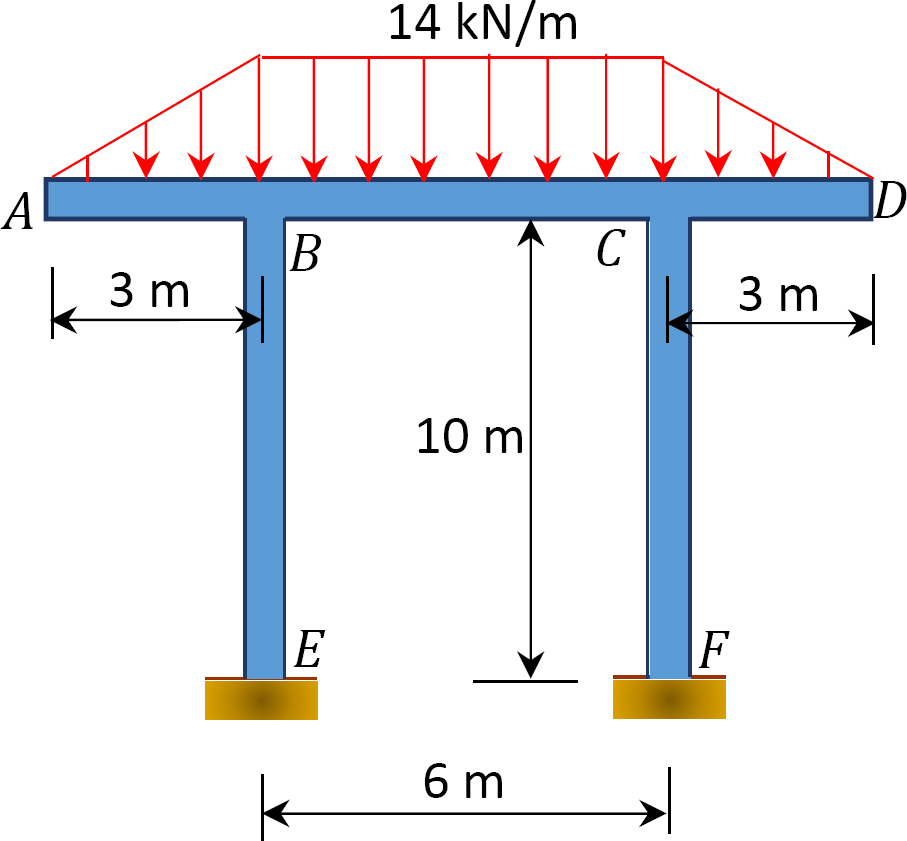
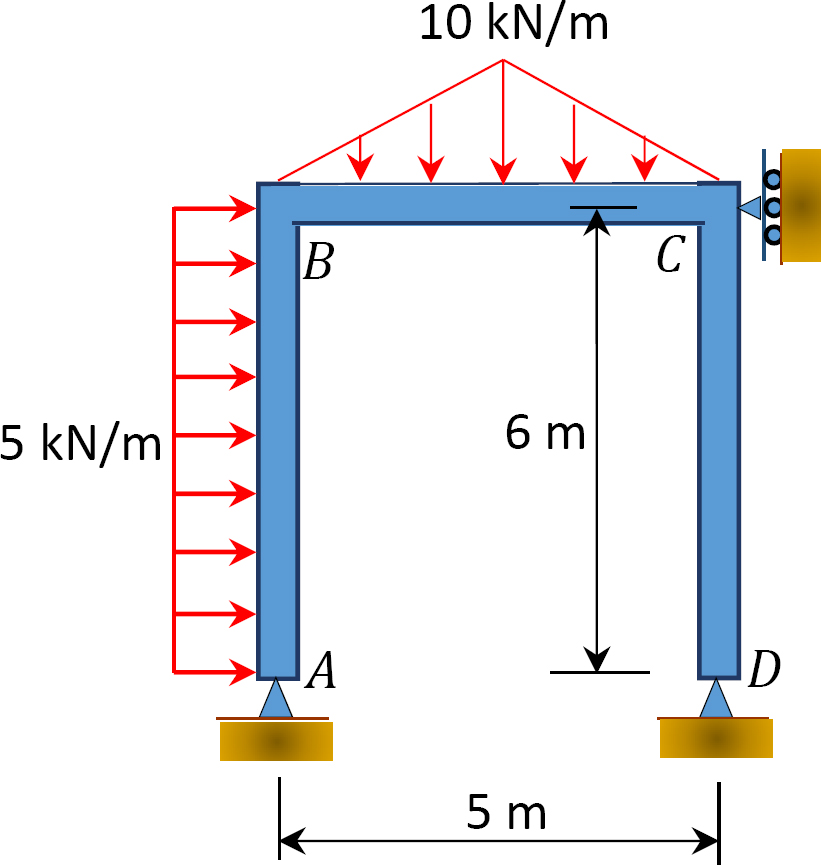
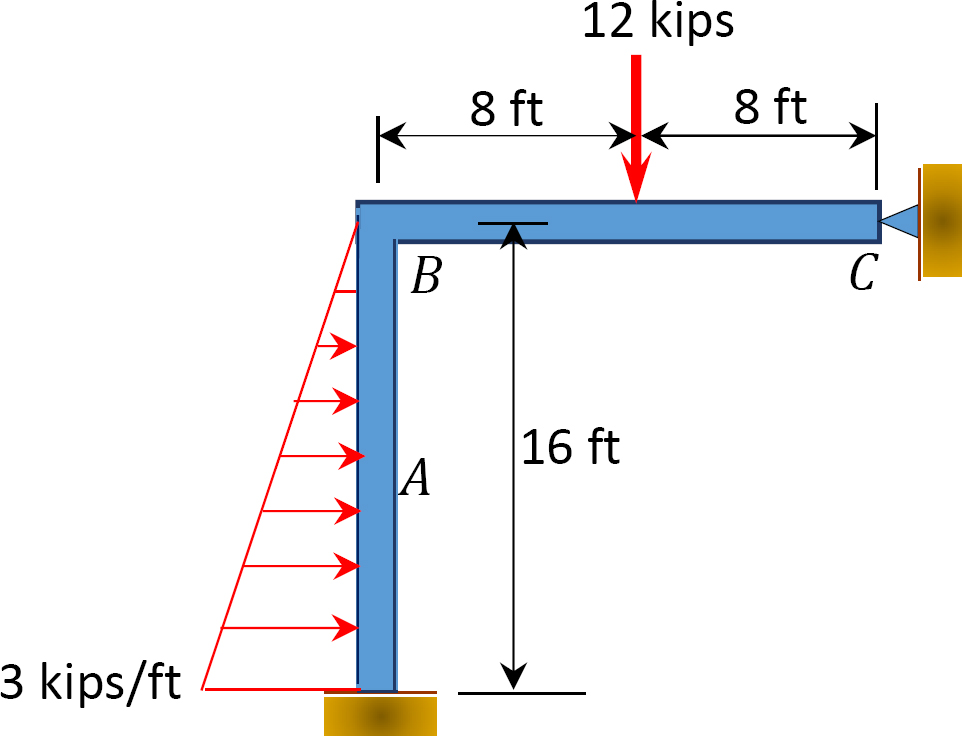
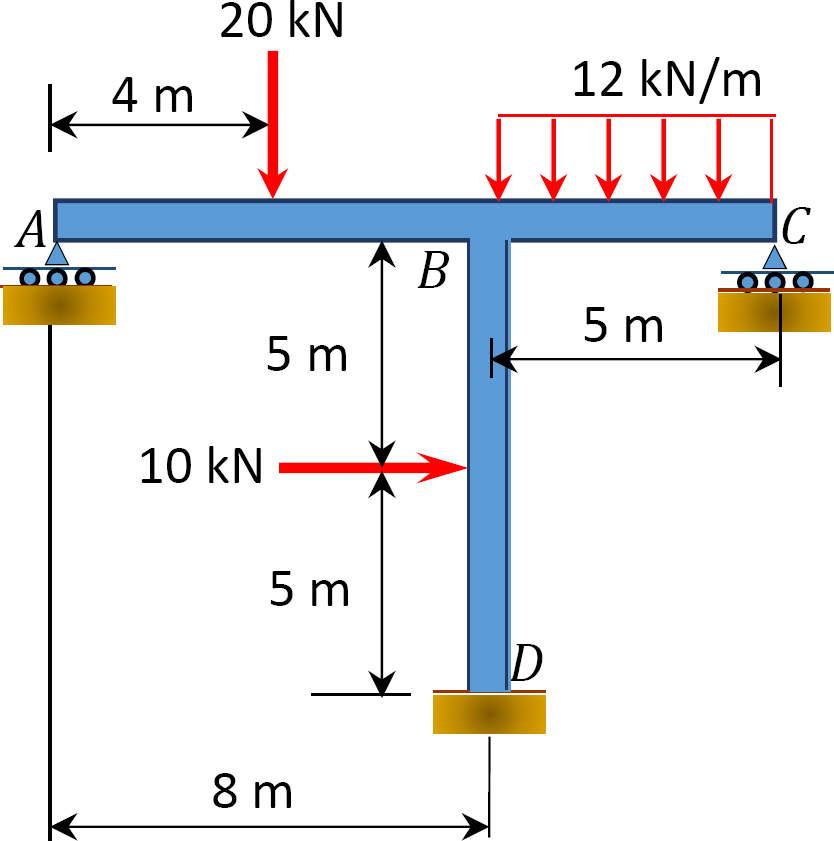
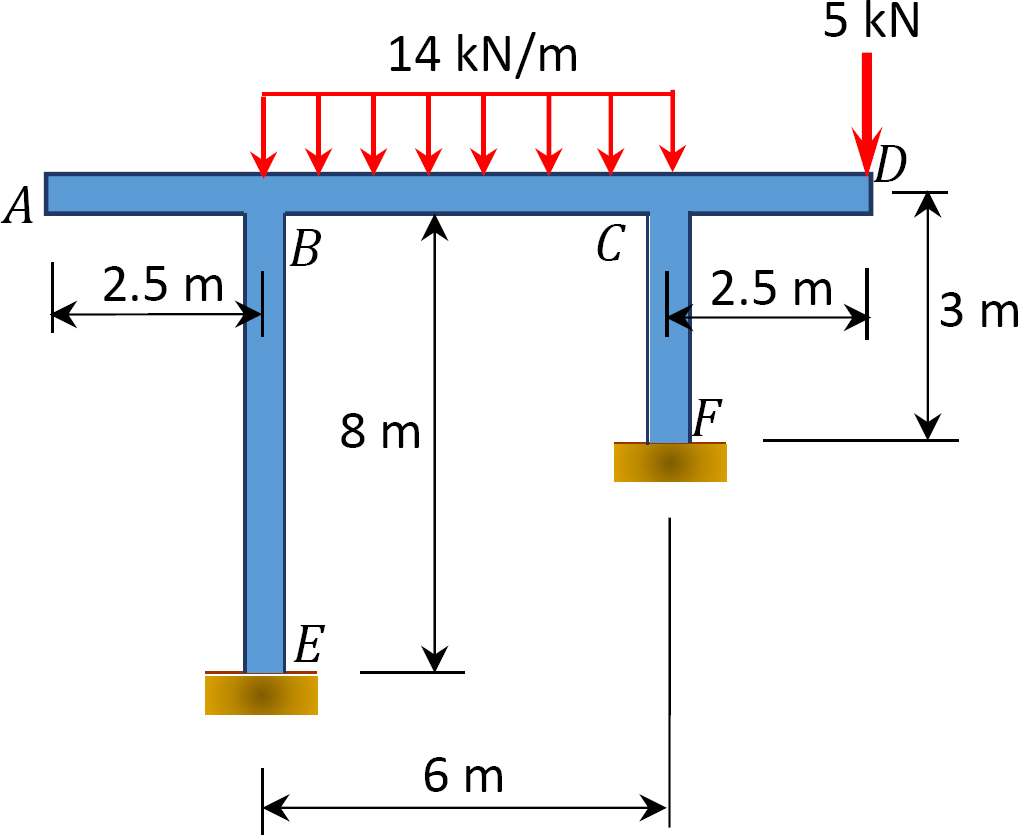
12.1 Use the moment distribution method to compute the end moment of members of the beams shown in Figure P12.1 through Figure P12.12 and draw the bending moment and shear force diagrams. EI = constant.
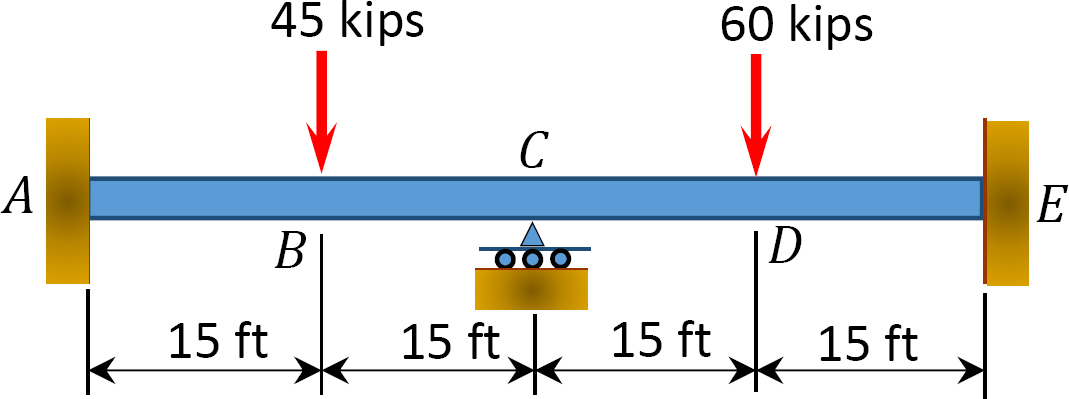
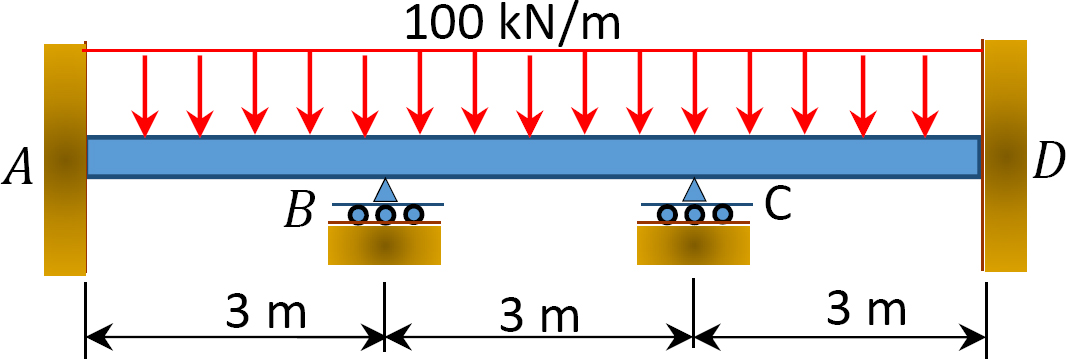
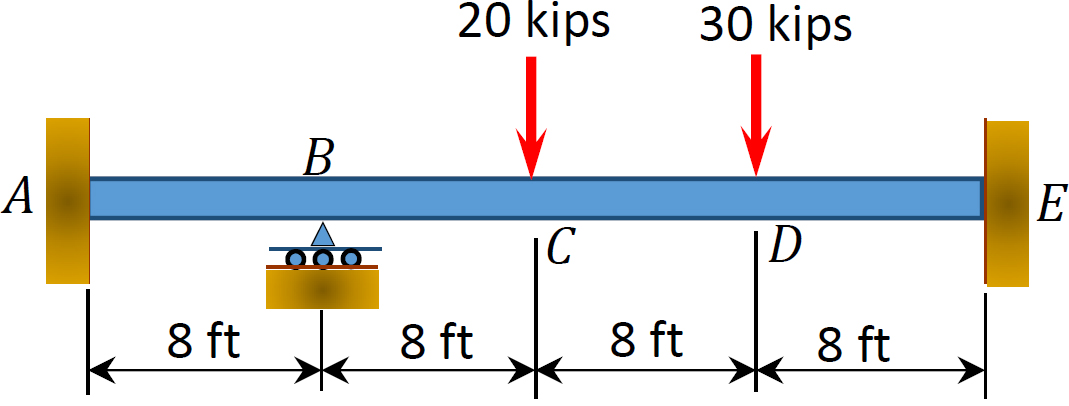
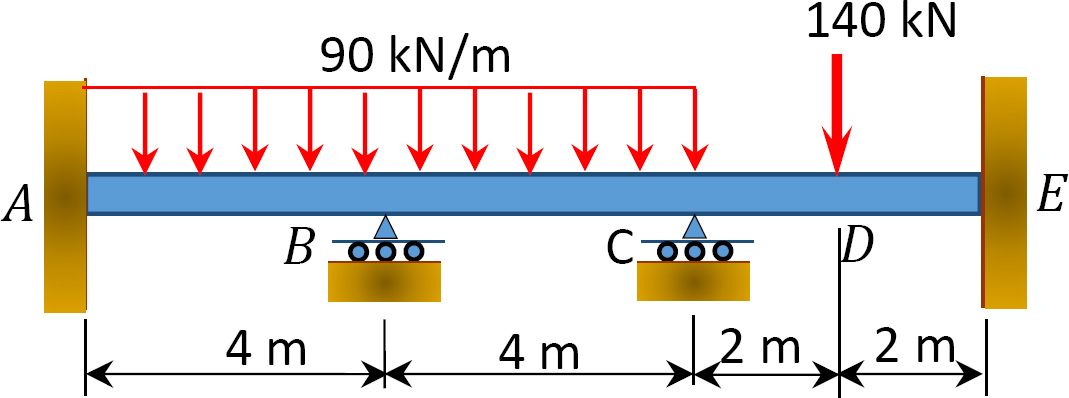
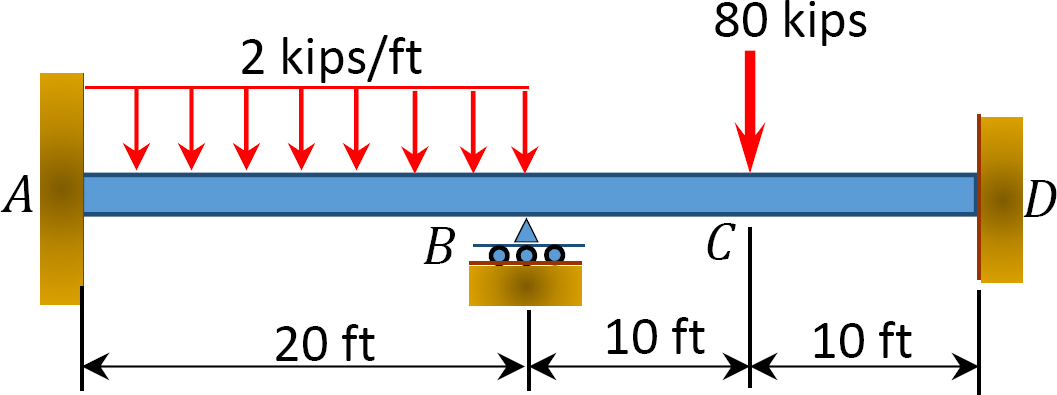
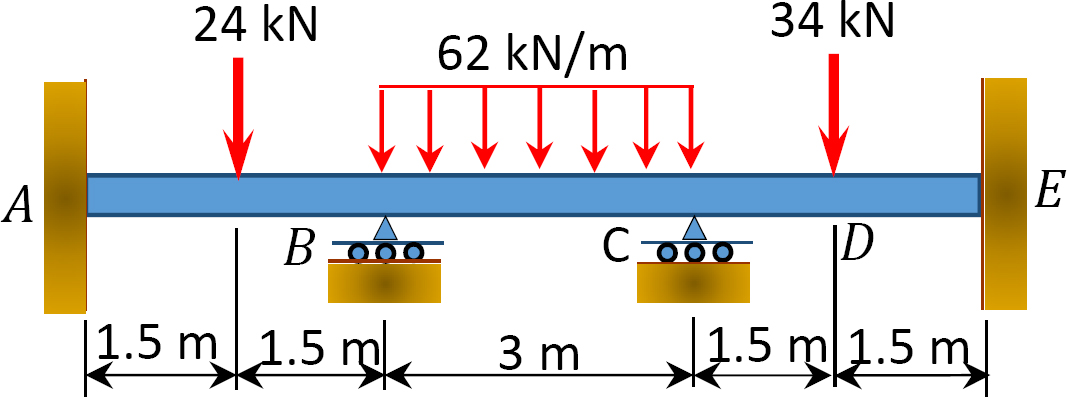
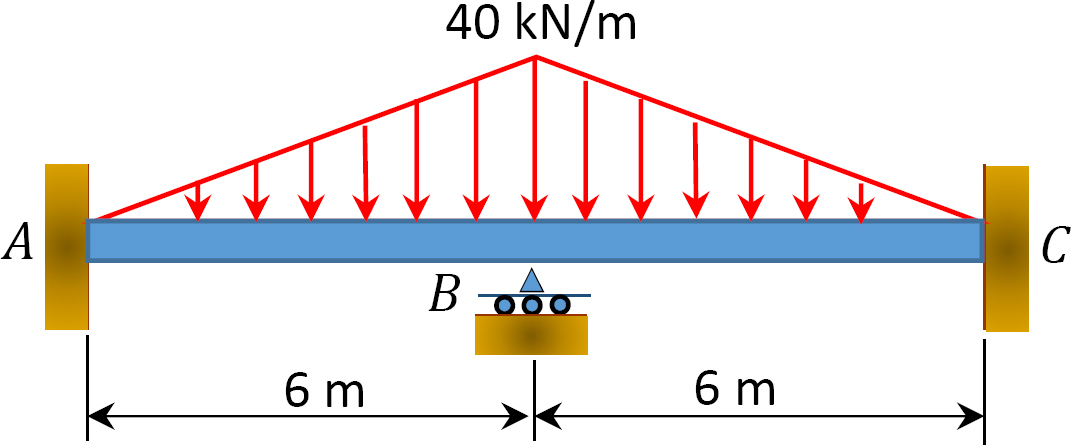
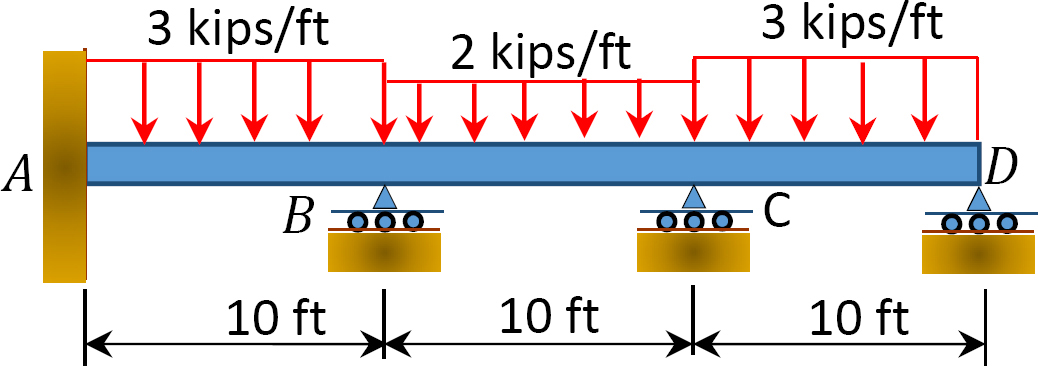
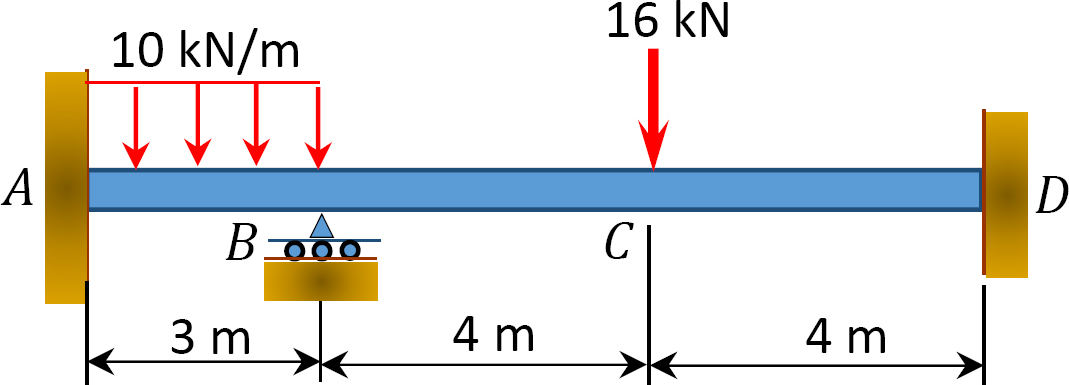
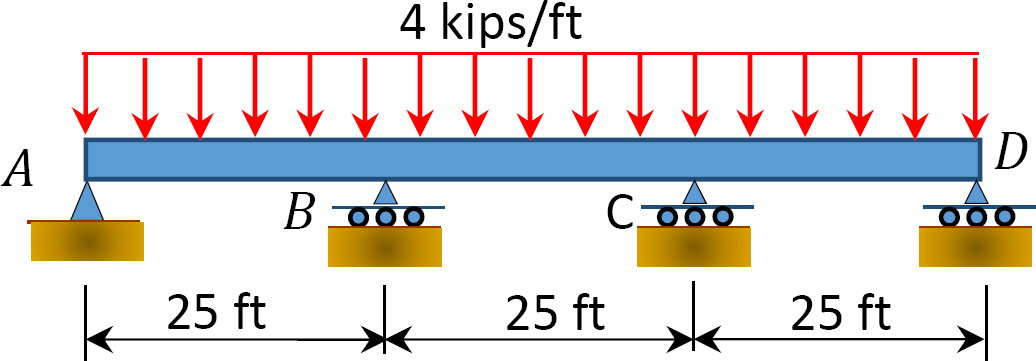
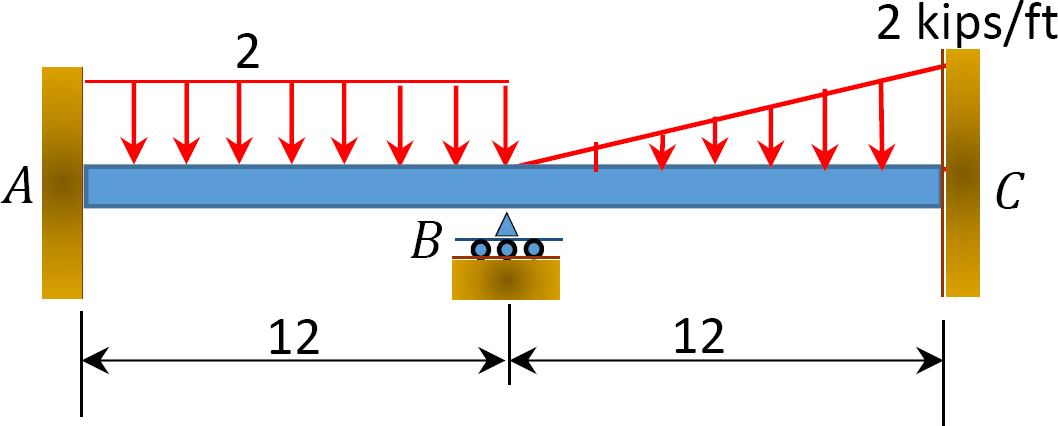
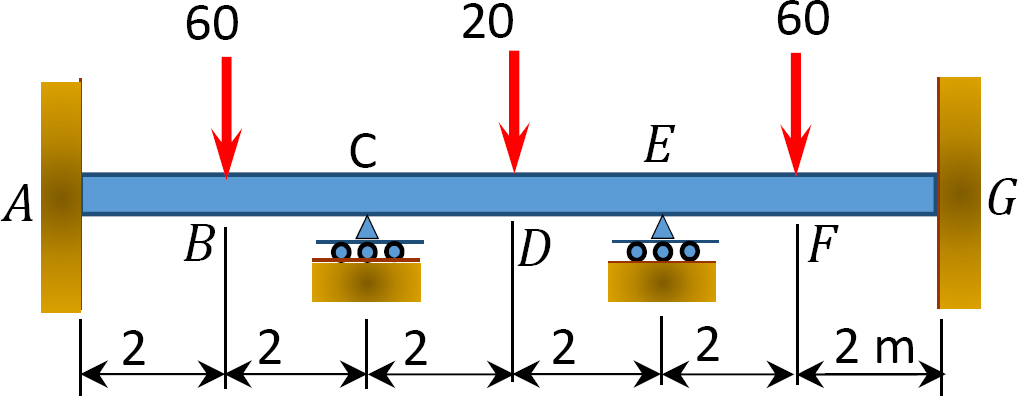
12.2 Use the moment distribution method to compute the end moment of the members of the frames shown in Figure P12.13 through Figure 12.20 and draw the bending moment and shear force diagrams. EI = constant.