6.5: Implementing 2D Transforms
- Page ID
- 13742
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This chapter uses WebGL for 2D drawing. Of course, the real motivation for using WebGL is to have high-performance 3D graphics on the web. We will turn to that in the next chapter. With WebGL, implementing transformations is the responsibility of the programmer, which adds a level of complexity compared to OpenGL 1.1. But before we attempt to deal with that complexity in three dimensions, this short section shows how to implement transforms and hierarchical modeling in a 2D context.
Transforms in GLSL
Transforms in 2D were covered in Section 2.3. To review: The basic transforms are scaling, rotation, and translation. A sequence of such transformations can be combined into a single affine transform. A 2D affine transform maps a point (x1,y1) to the point (x2,y2) given by formulas of the form
x2 = a*x1 + c*y1 + e
y2 = b*x1 + d*y1 + f
where a, b, c, d, e, and f are constants. As explained in Subsection 2.3.8, this transform can be represented as the 3-by-3 matrix
\[ \begin{bmatrix} a & c & e \\ b & d & f \\ 0 & 0 & 1 \end{bmatrix}\nonumber \]
With this representation, a point (x,y) becomes the three-dimensional vector (x,y,1), and the transformation can be implemented as multiplication of the vector by the matrix.
To apply a transformation to a primitive, each vertex of the primitive has to be multiplied by the transformation matrix. In GLSL, the natural place to do that is in the vertex shader. Technically, it would be possible to do the multiplication on the JavaScript side, but GLSL can do it more efficiently, since it can work on multiple vertices in parallel, and it is likely that the GPU has efficient hardware support for matrix math. (It is, by the way, a property of affine transformations that it suffices to apply them at the vertices of a primitive. Interpolation of the transformed vertex coordinates to the interior pixels of the primitive will given the correct result; that is, it gives the same answer as interpolating the original vertex coordinates and then applying the transformation in the fragment shader.)
In GLSL, the type mat3 represents 3-by-3 matrices, and vec3 represents three-dimensional vectors. When applied to a mat3 and a vec3, the multiplication operator * computes the product. So, a transform can applied using a simple GLSL assignment statement such as
transformedCoords = transformMatrix * originalCoords;
For 2D drawing, the original coordinates are likely to come into the vertex shader as an attribute of type vec2. We need to make the attribute value into a vec3 by adding 1.0 as the z-coordinate. The transformation matrix is likely to be a uniform variable, to allow the JavaScript side to specify the transformation. This leads to the following minimal vertex shader for working with 2D transforms:
attribute vec2 a_coords;
uniform mat3 u_transform;
void main() {
vec3 transformedCoords = u_transform * vec3(a coords,1.0);
gl Position = vec4(transformedCoords.xy, 0.0, 1.0);
}
In the last line, the value for gl_Position must be a vec4. For a 2D point, the z-coordinate should be 0.0, not 1.0, so we use only the x- and y-coordinates from transformedCoords.
On the JavaScript side, the function gl.uniformMatrix3fv is used to specify a value for a uniform of type mat3 (Subsection 6.3.3). To use it, the nine elements of the matrix must be stored in an array in column-major order. For loading an affine transformation matrix into a mat3, the command would be something like this:
gl.uniformMatrix3fv(u_transform_location, false, [ a, b, 0, c, d, 0, e, f, 1 ]
Transforms in JavaScript
To work with transforms on the JavaScript side, we need a way to represent the transforms. We also need to keep track of a “current transform” that is the product all the individual modeling transformations that are in effect. The current transformation changes whenever a transformation such as rotation or translation is applied. We need a way to save a copy of the current transform before drawing a complex object and to restore it after drawing. Typically, a stack of transforms is used for that purpose. You should be well familiar with this pattern from both 2D and 3D graphics. The difference here is that the data structures and operations that we need are not built into the standard API, so we need some extra JavaScript code to implement them.
As an example, I have written a JavaScript class, AffineTransform2D, to represent affine transforms in 2D. This is a very minimal implementation. The data for an object of type AffineTransform2D consists of the numbers a, b, c, d, e, and f in the transform matrix. There are methods in the class for multiplying the transform by scaling, rotation, and translation transforms. These methods modify the transform to which they are applied, by multiplying it on the right by the appropriate matrix. Here is a full description of the API, where transform is an object of type AffineTransform2D:
- transform = newAffineTransform2D(a,b,c,d,e,f) — creates a AffineTransform2D with the matrix shown at the beginning of this section.
- transform = new AffineTransform2D() — creates an AffineTransform2D representing the identity transform.
- transform = new AffineTransform2D(original) — where original is an AffineTransform2D, creates a copy of original.
- transform.rotate(r) — modifies transform by composing it with the rotation matrix for a rotation by r radians.
- transform.translate(dx,dy) — modifies transform by composing it with the translation matrix for a translation by (dx,dy).
- transform.scale(sx,sy) — modifies transform by composing it with the scaling matrix for scaling by a factor of sx horizontally and sy vertically.
- transform.scale(s) — does a uniform scaling, the same as transform.scale(s,s).
- array = transform.getMat3() — returns an array of nine numbers containing the matrix for transform in column-major order.
In fact, an AffineTransform2D object does not represent an affine transformation as a matrix. Instead, it stores the coefficients a, b, c, d, e, and f as properties of the object. With this representation, the scale method in the AffineTransform2D class can defined as follows:
AffineTransform2D.prototype.scale = function(sx,sy) {
if (sy === undefined) { // If sy is not specified, do uniform scaling.
sy = sx;
}
this.a *= sx;
this.b *= sx;
this.c *= sy;
this.d *= sy;
return this;
}
This code multiplies the transform represented by “this” object by a scaling matrix, on the right. Other methods have similar definitions, but you don’t need to understand the code in order to use the API.
Before a primitive is drawn, the current transform must sent as a mat3 into the vertex shader, where the mat3 is needed to transform the vertices of the primitive. The method transform.getMat3() returns the transform as an array that can be passed to gl.uniformMatrix3fv, which sends it to the shader program.
To implement the stack of transformations, we can use an array of objects of type AffineTransform2D. In JavaScript, an array does not have a fixed length, and it comes with push() and pop() methods that make it possible to use the array as a stack. For convenience, we can define functions pushTransform() and popTransform() to manipulate the stack. Here, the current transform is stored in a global variable named transform:
var transform = new AffineTransform2D(); // Initially the identity.
var transformStack = []; // An array to serve as the transform stack.
/**
* Push a copy of the current transform onto the transform stack.
*/
function pushTransform() {
transformStack.push( new AffineTransform2D(transform) );
}
/**
* Remove the top item from the transform stack, and set it to be the current
* transform. If the stack is empty, nothing is done (and there is no error).
*/
function popTransform() {
if (transformStack.length > 0) {
transform = transformStack.pop();
}
}
This code is from the sample program webgl/simple-hierarchy2D.html, which demonstrates using AffineTransform2D and a stack of transforms to implement hierarchical modeling. Here is a screenshot of one of the objects drawn by that program:
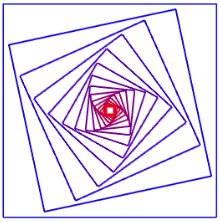
and here’s the code that draws it:
function square() {
gl.uniformMatrix3fv(u_transform_loc, false, transform.getMat3());
gl.bindBuffer(gl.ARRAY_BUFFER, squareCoordsVBO);
gl.vertexAttribPointer(a_coords_loc, 2, gl.FLOAT, false, 0, 0);
gl.drawArrays(gl.LINE_LOOP, 0, 4);
}
function nestedSquares() {
gl.uniform3f( u_color_loc, 0, 0, 1); // Set color to blue.
square();
for (var i = 1; i < 16; i++) {
gl.uniform3f( u_color_loc, i/16, 0, 1 - i/16); // Red/Blue mixture.
transform.scale(0.8);
transform.rotate(framenumber / 200);
square();
}
}
The function square() draws a square that has size 1 and is centered at (0,0) in its own object coordinate system. The coordinates for the square have been stored in a buffer, squareCoordsVBO, and a_coords_loc is the location of an attribute variable in the shader program. The variable transform holds the current modeling transform that must be applied to the square. It is sent to the shader program by calling
gl.uniformMatrix3fv(u_transform_loc, false, transform.getMat3());
The second function, nestedSquares(), draws 16 squares. Between the squares, it modifies the modeling transform with
transform.scale(0.8);
transform.rotate(framenumber / 200);
The effect of these commands is cumulative, so that each square is a little smaller than the previous one, and is rotated a bit more than the previous one. The amount of rotation depends on the frame number in an animation.
The nested squares are one of three compound objects drawn by the program. The function draws the nested squares centered at (0,0). In the main draw() routine, I wanted to move them and make them a little smaller. So, they are drawn using the code:
pushTransform(); transform.translate(-0.5,0.5); // Move center of squares to (-0.5, 0.5). transform.scale(0.85); // Reduce size from 1 to 0.85. nestedSquares(); popTransform();
The pushTransform() and popTransform() ensure that all of the changes made to the modeling transform while drawing the squares will have no effect on other objects that are drawn later. Transforms are, as always, applied to objects in the opposite of the order in which they appear in the code.
I urge you to read the source code and take a look at what it draws. The essential ideas for working with transforms are all there. It would be good to understand them before we move on to 3D.


