1.6: Learning with gradient descent
- Page ID
- 3743
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Now that we have a design for our neural network, how can it learn to recognize digits? The first thing we'll need is a data set to learn from - a so-called training data set. We'll use the MNIST data set, which contains tens of thousands of scanned images of handwritten digits, together with their correct classifications. MNIST's name comes from the fact that it is a modified subset of two data sets collected by NIST, the United States' National Institute of Standards and Technology. Here's a few images from MNIST:
.png?revision=1&size=bestfit&width=359&height=56)
As you can see, these digits are, in fact, the same as those shown at the beginning of this chapter as a challenge to recognize. Of course, when testing our network we'll ask it to recognize images which aren't in the training set!
The MNIST data comes in two parts. The first part contains 60,000 images to be used as training data. These images are scanned handwriting samples from 250 people, half of whom were US Census Bureau employees, and half of whom were high school students. The images are greyscale and 28 by 28 pixels in size. The second part of the MNIST data set is 10,000 images to be used as test data. Again, these are 28 by 28 greyscale images. We'll use the test data to evaluate how well our neural network has learned to recognize digits. To make this a good test of performance, the test data was taken from a different set of 250 people than the original training data (albeit still a group split between Census Bureau employees and high school students). This helps give us confidence that our system can recognize digits from people whose writing it didn't see during training.
We'll use the notation \(x\) to denote a training input. It'll be convenient to regard each training input \(x\) as a \(28×28=784\)-dimensional vector. Each entry in the vector represents the grey value for a single pixel in the image. We'll denote the corresponding desired output by \(y=y(x)\), where \(y\) is a \(10\)-dimensional vector. For example, if a particular training image, \(x\), depicts a \(6\), then \(y(x)=(0,0,0,0,0,0,1,0,0,0)^T\) is the desired output from the network. Note that \(T\) here is the transpose operation, turning a row vector into an ordinary (column) vector.
What we'd like is an algorithm which lets us find weights and biases so that the output from the network approximates \(y(x)\) for all training inputs \(x\). To quantify how well we're achieving this goal we define a cost function*:
*Sometimes referred to as a loss or objective function. We use the term cost function throughout this book, but you should note the other terminology, since it's often used in research papers and other discussions of neural networks.
\[ C(w,b) ≡ \frac{1}{2n}\sum_x ∥ y(x)−a ∥^{2}.\]
Here, \(w\) denotes the collection of all weights in the network, \(b\) all the biases, nn is the total number of training inputs, aa is the vector of outputs from the network when \(x\) is input, and the sum is over all training inputs, \(x\). Of course, the output aa depends on \(x\), \(w\) and \(b\), but to keep the notation simple I haven't explicitly indicated this dependence. The notation \(∥v∥\) just denotes the usual length function for a vector \(v\). We'll call \(C\) the quadratic cost function; it's also sometimes known as the mean squared error or just MSE. Inspecting the form of the quadratic cost function, we see that \(C(w,b)\) is non-negative, since every term in the sum is non-negative. Furthermore, the cost \(C(w,b)\) becomes small, i.e., \(C(w,b)≈0\), precisely when \(y(x)\) is approximately equal to the output, aa, for all training inputs, \(x\). So our training algorithm has done a good job if it can find weights and biases so that \(C(w,b)≈0\). By contrast, it's not doing so well when \(C(w,b)\) is large - that would mean that \(y(x)\) is not close to the output aa for a large number of inputs. So the aim of our training algorithm will be to minimize the cost \(C(w,b)\) as a function of the weights and biases. In other words, we want to find a set of weights and biases which make the cost as small as possible. We'll do that using an algorithm known as gradient descent.
Why introduce the quadratic cost ? After all, aren't we primarily interested in the number of images correctly classified by the network? Why not try to maximize that number directly, rather than minimizing a proxy measure like the quadratic cost ? The problem with that is that the number of images correctly classified is not a smooth function of the weights and biases in the network. For the most part, making small changes to the weights and biases won't cause any change at all in the number of training images classified correctly. That makes it difficult to figure out how to change the weights and biases to get improved performance. If we instead use a smooth cost function like the quadratic cost it turns out to be easy to figure out how to make small changes in the weights and biases so as to get an improvement in the cost. That's why we focus first on minimizing the quadratic cost, and only after that will we examine the classification accuracy.
Even given that we want to use a smooth cost function, you may still wonder why we choose the quadratic function used in Equation (1.6.1). Isn't this a rather ad hoc choice? Perhaps if we chose a different cost function we'd get a totally different set of minimizing weights and biases? This is a valid concern, and later we'll revisit the cost function, and make some modifications. However, the quadratic cost function of Equation (1.6.1) works perfectly well for understanding the basics of learning in neural networks, so we'll stick with it for now.
Recapping, our goal in training a neural network is to find weights and biases which minimize the quadratic cost function \(C(w,b)\). This is a well-posed problem, but it's got a lot of distracting structure as currently posed - the interpretation of ww and bb as weights and biases, the \(σ\) function lurking in the background, the choice of network architecture, MNIST, and so on. It turns out that we can understand a tremendous amount by ignoring most of that structure, and just concentrating on the minimization aspect. So for now we're going to forget all about the specific form of the cost function, the connection to neural networks, and so on. Instead, we're going to imagine that we've simply been given a function of many variables and we want to minimize that function. We're going to develop a technique called gradient descent which can be used to solve such minimization problems. Then we'll come back to the specific function we want to minimize for neural networks.
Okay, let's suppose we're trying to minimize some function, \(C(v)\). This could be any real-valued function of many variables, \(v = v1,v2,…\).Note that I've replaced the \(w\) and \(b\) notation by \(v\) to emphasize that this could be any function - we're not specifically thinking in the neural networks context any more. To minimize \(C(v)\) it helps to imagine \(C\) as a function of just two variables, which we'll call \(v1\) and \(v2\):
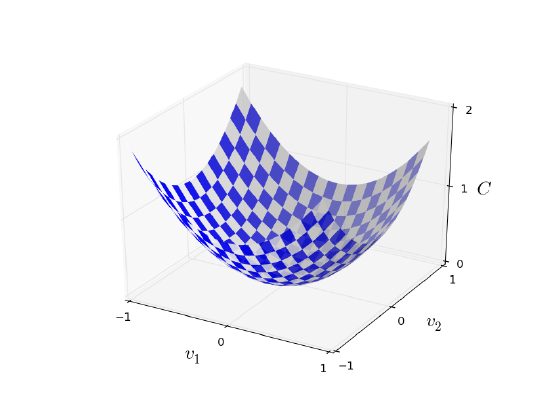
What we'd like is to find where \(C\) achieves its global minimum. Now, of course, for the function plotted above, we can eyeball the graph and find the minimum. In that sense, I've perhaps shown slightly too simple a function! A general function, \(C\), may be a complicated function of many variables, and it won't usually be possible to just eyeball the graph to find the minimum.
One way of attacking the problem is to use calculus to try to find the minimum analytically. We could compute derivatives and then try using them to find places where \(C\) is an extremum. With some luck that might work when \(C\) is a function of just one or a few variables. But it'll turn into a nightmare when we have many more variables. And for neural networks we'll often want far more variables - the biggest neural networks have cost functions which depend on billions of weights and biases in an extremely complicated way. Using calculus to minimize that just won't work!
(After asserting that we'll gain insight by imagining \(C\) as a function of just two variables, I've turned around twice in two paragraphs and said, "hey, but what if it's a function of many more than two variables?" Sorry about that. Please believe me when I say that it really does help to imagine \(C\) as a function of two variables. It just happens that sometimes that picture breaks down, and the last two paragraphs were dealing with such breakdowns. Good thinking about mathematics often involves juggling multiple intuitive pictures, learning when it's appropriate to use each picture, and when it's not.)
Okay, so calculus doesn't work. Fortunately, there is a beautiful analogy which suggests an algorithm which works pretty well. We start by thinking of our function as a kind of a valley. If you squint just a little at the plot above, that shouldn't be too hard. And we imagine a ball rolling down the slope of the valley. Our everyday experience tells us that the ball will eventually roll to the bottom of the valley. Perhaps we can use this idea as a way to find a minimum for the function? We'd randomly choose a starting point for an (imaginary) ball, and then simulate the motion of the ball as it rolled down to the bottom of the valley. We could do this simulation simply by computing derivatives (and perhaps some second derivatives) of \(C\) - those derivatives would tell us everything we need to know about the local "shape" of the valley, and therefore how our ball should roll.
Based on what I've just written, you might suppose that we'll be trying to write down Newton's equations of motion for the ball, considering the effects of friction and gravity, and so on. Actually, we're not going to take the ball-rolling analogy quite that seriously - we're devising an algorithm to minimize \(C\), not developing an accurate simulation of the laws of physics! The ball's-eye view is meant to stimulate our imagination, not constrain our thinking. So rather than get into all the messy details of physics, let's simply ask ourselves: if we were declared God for a day, and could make up our own laws of physics, dictating to the ball how it should roll, what law or laws of motion could we pick that would make it so the ball always rolled to the bottom of the valley?
To make this question more precise, let's think about what happens when we move the ball a small amount \(Δv_1\) in the \(v_1\) direction, and a small amount \(Δv_2\) in the \(v_2\) direction. Calculus tells us that \(C\) changes as follows:
\[ ΔC ≈ \frac{∂C}{∂v_1} Δv_1 + \frac{∂C}{∂v_2} Δv_2 \]
We're going to find a way of choosing \(Δv_1\) and \(Δv_2\) so as to make \(ΔC\) negative; i.e., we'll choose them so the ball is rolling down into the valley. To figure out how to make such a choice it helps to define \(Δv\) to be the vector of changes in \(v\), \(Δv ≡ (Δv_1,Δv_2)\)^T, where \(T\) is again the transpose operation, turning row vectors into column vectors. We'll also define the gradient of \(C\) to be the vector of partial derivatives, \((\frac{∂C}{∂v_1},\frac{∂C}{∂v_2})^T\). We denote the gradient vector by \( ∇C \) i.e.:
\[ ∇C ≡ \Big( \frac{∂C}{∂v_1} , \frac{∂C}{∂v_2}\Big)^T \]
In a moment we'll rewrite the change \(ΔC\) in terms of \(Δv\) and the gradient, \(∇C\). Before getting to that, though, I want to clarify something that sometimes gets people hung up on the gradient. When meeting the \(∇C\) notation for the first time, people sometimes wonder how they should think about the \(∇\) symbol. What, exactly, does \(∇\) mean? In fact, it's perfectly fine to think of \(∇C\) as a single mathematical object - the vector defined above - which happens to be written using two symbols. In this point of view, \(∇\) is just a piece of notational flag-waving, telling you "hey, \(∇C\) is a gradient vector". There are more advanced points of view where \(∇\) can be viewed as an independent mathematical entity in its own right (for example, as a differential operator), but we won't need such points of view.
With these definitions, the expression (1.6.2) for \(ΔC\) can be rewritten as
\[ ΔC ≈ ∇C⋅Δv \]
This equation helps explain why ∇C∇C is called the gradient vector: \(∇C\) relates changes in \(v\) to changes in \(C\), just as we'd expect something called a gradient to do. But what's really exciting about the equation is that it lets us see how to choose \(Δv\) so as to make \(ΔC\) negative. In particular, suppose we choose
\[ Δv = −η∇C \]
where \(η\) is a small, positive parameter (known as the learning rate). Then Equation (1.6.4) tells us that \(ΔC ≈ −η∇C⋅∇C = −η∥∇C∥^2 /). Because \(∥∇C∥^2 \ge 0,\) this guarantees that \(ΔC\le0\), i.e., \(C\) will always decrease, never increase, if we change \(v\) according to the prescription in (1.6.5). (Within, of course, the limits of the approximation in Equation (1.6.4)). This is exactly the property we wanted! And so we'll take Equation (1.6.5) to define the "law of motion" for the ball in our gradient descent algorithm. That is, we'll use Equation (1.6.5) to compute a value for \(Δv\), then move the ball's position \(v\) by that amount:
\[ v → v′ = v−η∇C \]
Then we'll use this update rule again, to make another move. If we keep doing this, over and over, we'll keep decreasing \(C\) until - we hope - we reach a global minimum.
Summing up, the way the gradient descent algorithm works is to repeatedly compute the gradient \(∇C\), and then to move in the opposite direction, "falling down" the slope of the valley. We can visualize it like this:
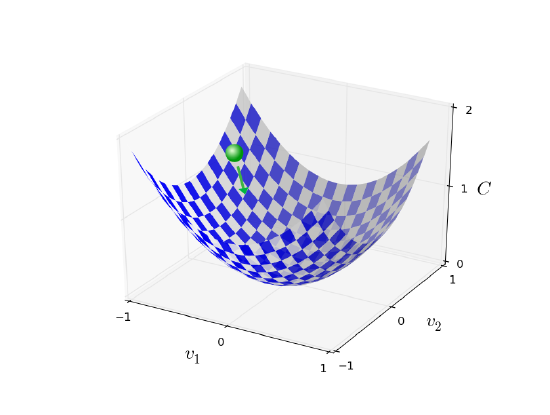
Notice that with this rule gradient descent doesn't reproduce real physical motion. In real life a ball has momentum, and that momentum may allow it to roll across the slope, or even (momentarily) roll uphill. It's only after the effects of friction set in that the ball is guaranteed to roll down into the valley. By contrast, our rule for choosing \(Δv\) just says "go down, right now". That's still a pretty good rule for finding the minimum!
To make gradient descent work correctly, we need to choose the learning rate ηη to be small enough that Equation (1.6.4) is a good approximation. If we don't, we might end up with \(ΔC\gt0\), which obviously would not be good! At the same time, we don't want \(η\) to be too small, since that will make the changes \(Δv\) tiny, and thus the gradient descent algorithm will work very slowly. In practical implementations, \(η\) is often varied so that Equation (1.6.4) remains a good approximation, but the algorithm isn't too slow. We'll see later how this works.
I've explained gradient descent when \(C\) is a function of just two variables. But, in fact, everything works just as well even when \(C\) is a function of many more variables. Suppose in particular that \(C\) is a function of \(m\) variables, \(v_1,…,v_m\). Then the change \(ΔC\) in \(C\) produced by a small change \(Δv= (Δv_1,…,Δv_m)^T\) is
\[ ΔC ≈ ∇C⋅Δv \]
where the gradient \(∇C\) is the vector
\[ ∇C ≡ \Big(\frac{∂C}{∂v_1},…,\frac{∂C}{∂v_m}\Big)^T \]
Just as for the two variable case, we can choose
\[ Δv = −η∇C \]
and we're guaranteed that our (approximate) expression (1.6.7) for \(ΔC\) will be negative. This gives us a way of following the gradient to a minimum, even when \(C\) is a function of many variables, by repeatedly applying the update rule
\[ v→v′ = v−η∇C \]
You can think of this update rule as defining the gradient descent algorithm. It gives us a way of repeatedly changing the position vv in order to find a minimum of the function \(C\). The rule doesn't always work - several things can go wrong and prevent gradient descent from finding the global minimum of \(C\), a point we'll return to explore in later chapters. But, in practice gradient descent often works extremely well, and in neural networks we'll find that it's a powerful way of minimizing the cost function, and so helping the net learn.
Indeed, there's even a sense in which gradient descent is the optimal strategy for searching for a minimum. Let's suppose that we're trying to make a move \(Δv\) in position so as to decrease \(C\) as much as possible. This is equivalent to minimizing \(ΔC ≈ ∇C⋅Δv\). We'll constrain the size of the move so that \(∥Δv∥ = ϵ \) for some small fixed \(ϵ\gt0\). In other words, we want a move that is a small step of a fixed size, and we're trying to find the movement direction which decreases \(C\) as much as possible. It can be proved that the choice of \(Δv\) which minimizes \(∇C⋅Δv\) is \(Δv = −η∇C\), where \(η = ϵ / ∥∇C∥\)is determined by the size constraint \(∥Δv∥ = ϵ\). So gradient descent can be viewed as a way of taking small steps in the direction which does the most to immediately decrease \(C\).
Exercises
- Prove the assertion of the last paragraph. Hint: If you're not already familiar with the Cauchy-Schwarz inequality, you may find it helpful to familiarize yourself with it.
- I explained gradient descent when \(C\) is a function of two variables, and when it's a function of more than two variables. What happens when \(C\) is a function of just one variable? Can you provide a geometric interpretation of what gradient descent is doing in the one-dimensional case?
People have investigated many variations of gradient descent, including variations that more closely mimic a real physical ball. These ball-mimicking variations have some advantages, but also have a major disadvantage: it turns out to be necessary to compute second partial derivatives of \(C\), and this can be quite costly. To see why it's costly, suppose we want to compute all the second partial derivatives \(∂^2C/∂v_j∂v_k\). If there are a million such \(v_j\) variables then we'd need to compute something like a trillion (i.e., a million squared) second partial derivatives*
*Actually, more like half a trillion, since \(∂^2C/∂v_j∂v_k = ∂^2C/∂v_k∂v_j\) Still, you get the point !
That's going to be computationally costly. With that said, there are tricks for avoiding this kind of problem, and finding alternatives to gradient descent is an active area of investigation. But in this book we'll use gradient descent (and variations) as our main approach to learning in neural networks.
How can we apply gradient descent to learn in a neural network? The idea is to use gradient descent to find the weights \(w_k\) and biases \(b_l\) which minimize the cost in Equation (1.6.1). To see how this works, let's restate the gradient descent update rule, with the weights and biases replacing the variables \(v_j\). In other words, our "position" now has components \(w_k\) and \(b_l\), and the gradient vector \(∇C\) has corresponding components \(∂C/∂w_k\) and \(∂C/∂b_l\). Writing out the gradient descent update rule in terms of components, we have
\[ w_k → w′_k = w_k − η\frac{∂C}{∂w_k} \]
\[ b_l → b′_l = b_l − η\frac{∂C}{∂b_l} \]
By repeatedly applying this update rule we can "roll down the hill", and hopefully find a minimum of the cost function. In other words, this is a rule which can be used to learn in a neural network.
There are a number of challenges in applying the gradient descent rule. We'll look into those in depth in later chapters. But for now I just want to mention one problem. To understand what the problem is, let's look back at the quadratic cost in Equation (1.6.1). Notice that this cost function has the form \(C=\frac{1}{n}\sum_x{C_x}\), that is, it's an average over costs \(C_x ≡ \frac{∥y(x)−a∥}{2}\) for individual training examples. In practice, to compute the gradient \(∇C\) we need to compute the gradients \(∇C_x\) separately for each training input, \(x\), and then average them, \(∇C=\frac{1}{n}\sum_x{∇C_x}\). Unfortunately, when the number of training inputs is very large this can take a long time, and learning thus occurs slowly.
An idea called stochastic gradient descent can be used to speed up learning. The idea is to estimate the gradient \(∇C\) by computing \(∇C_x\) for a small sample of randomly chosen training inputs. By averaging over this small sample it turns out that we can quickly get a good estimate of the true gradient \(∇C\), and this helps speed up gradient descent, and thus learning.
To make these ideas more precise, stochastic gradient descent works by randomly picking out a small number mm of randomly chosen training inputs. We'll label those random training inputs \(X_1,X_2,…,X_m\), and refer to them as a mini-batch. Provided the sample size mm is large enough we expect that the average value of the \(∇C_{X_j}\) will be roughly equal to the average over all \(∇C_x\), that is,
\[ \frac{ \sum_{j=1}^m ∇C_{X_j} }{m} ≈ \frac{ \sum_x ∇C_x}{n} = ∇C \]
where the second sum is over the entire set of training data. Swapping sides we get
\[ ∇C ≈ \frac{1}{m} \sum{j=1}^m ∇C_{X_j}, \]
confirming that we can estimate the overall gradient by computing gradients just for the randomly chosen mini-batch.
To connect this explicitly to learning in neural networks, suppose \(w_k\) and \(b_l\) denote the weights and biases in our neural network. Then stochastic gradient descent works by picking out a randomly chosen mini-batch of training inputs, and training with those,
\[ w_k →w′_k = wk−\frac{η}{m}\sum_j\frac{∂C_{X_j}}{∂w_k} \]
\[ b_l →b′_l = b_l−\frac{η}{m}\sum_j\frac{∂C_{X_j}}{∂b_l} \]
where the sums are over all the training examples \(X_j\) in the current mini-batch. Then we pick out another randomly chosen mini-batch and train with those. And so on, until we've exhausted the training inputs, which is said to complete an epoch of training. At that point we start over with a new training epoch.
Incidentally, it's worth noting that conventions vary about scaling of the cost function and of mini-batch updates to the weights and biases. In Equation (1.6.1) we scaled the overall cost function by a factor \(\frac{1}{n}\). People sometimes omit the \(\frac{1}{n}\), summing over the costs of individual training examples instead of averaging. This is particularly useful when the total number of training examples isn't known in advance. This can occur if more training data is being generated in real time, for instance. And, in a similar way, the mini-batch update rules (1.6.15) and (1.6.16) sometimes omit the \(\frac{1}{m}\) term out the front of the sums. Conceptually this makes little difference, since it's equivalent to rescaling the learning rate \(η\). But when doing detailed comparisons of different work it's worth watching out for.
We can think of stochastic gradient descent as being like political polling: it's much easier to sample a small mini-batch than it is to apply gradient descent to the full batch, just as carrying out a poll is easier than running a full election. For example, if we have a training set of size \(n=60,000\), as in MNIST, and choose a mini-batch size of (say) \(m=10\), this means we'll get a factor of \(6,000\),speedup in estimating the gradient! Of course, the estimate won't be perfect - there will be statistical fluctuations - but it doesn't need to be perfect: all we really care about is moving in a general direction that will help decrease \(C\), and that means we don't need an exact computation of the gradient. In practice, stochastic gradient descent is a commonly used and powerful technique for learning in neural networks, and it's the basis for most of the learning techniques we'll develop in this book.
Exercise
- An extreme version of gradient descent is to use a mini-batch size of just 1. That is, given a training input, \(x\), we update our weights and biases according to the rules \(w_k→w′_k = wk−η∂C_x/∂w_k and \(b_l→b′_l=b_l−η∂C_x/∂b_l\).Then we choose another training input, and update the weights and biases again. And so on, repeatedly. This procedure is known as online, on-line, or incremental learning. In online learning, a neural network learns from just one training input at a time (just as human beings do). Name one advantage and one disadvantage of online learning, compared to stochastic gradient descent with a mini-batch size of, say, 2020.
Let me conclude this section by discussing a point that sometimes bugs people new to gradient descent. In neural networks the cost \(C\) is, of course, a function of many variables - all the weights and biases - and so in some sense defines a surface in a very high-dimensional space. Some people get hung up thinking: "Hey, I have to be able to visualize all these extra dimensions". And they may start to worry: "I can't think in four dimensions, let alone five (or five million)". Is there some special ability they're missing, some ability that "real" super mathematicians have? Of course, the answer is no. Even most professional mathematicians can't visualize four dimensions especially well, if at all. The trick they use, instead, is to develop other ways of representing what's going on. That's exactly what we did above: we used an algebraic (rather than visual) representation of \(ΔC\) to figure out how to move so as to decrease \(C\). People who are good at thinking in high dimensions have a mental library containing many different techniques along these lines; our algebraic trick is just one example. Those techniques may not have the simplicity we're accustomed to when visualizing three dimensions, but once you build up a library of such techniques, you can get pretty good at thinking in high dimensions. I won't go into more detail here, but if you're interested then you may enjoy reading this discussion of some of the techniques professional mathematicians use to think in high dimensions. While some of the techniques discussed are quite complex, much of the best content is intuitive and accessible, and could be mastered by anyone.


