4.3: SkiplistList - An Efficient Random-Access List
- Page ID
- 8452
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A SkiplistList implements the List interface using a skiplist structure. In a SkiplistList, \(L_0\) contains the elements of the list in the order in which they appear in the list. As in a SkiplistSSet, elements can be added, removed, and accessed in \(O(\log \mathtt{n})\) time.
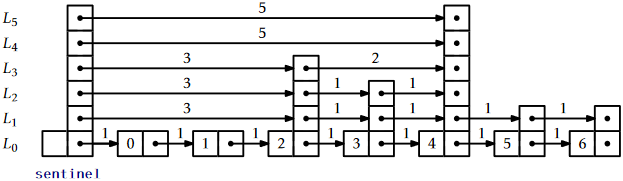
For this to be possible, we need a way to follow the search path for the \(\mathtt{i}\)th element in \(L_0\). The easiest way to do this is to define the notion of the length of an edge in some list, \(L_{\mathtt{r}}\). We define the length of every edge in \(L_{0}\) as 1. The length of an edge, \(\mathtt{e}\), in \(L_{\mathtt{r}}\), \(\mathtt{r}>0\), is defined as the sum of the lengths of the edges below \(\mathtt{e}\) in \(L_{\mathtt{r}-1}\). Equivalently, the length of \(\mathtt{e}\) is the number of edges in \(L_0\) below \(\mathtt{e}\). See Figure \(\PageIndex{1}\) for an example of a skiplist with the lengths of its edges shown. Since the edges of skiplists are stored in arrays, the lengths can be stored the same way:
class Node {
T x;
Node[] next;
int[] length;
@SuppressWarnings("unchecked")
Node(T ix, int h) {
x = ix;
next = (Node[])Array.newInstance(Node.class, h+1);
length = new int[h+1];
}
int height() {
return next.length - 1;
}
}
The useful property of this definition of length is that, if we are currently at a node that is at position \(\mathtt{j}\) in \(L_0\) and we follow an edge of length \(\ell\), then we move to a node whose position, in \(L_0\), is \(\mathtt{j}+\ell\). In this way, while following a search path, we can keep track of the position, \(\mathtt{j}\), of the current node in \(L_0\). When at a node, \(\mathtt{u}\), in \(L_{\mathtt{r}}\), we go right if \(\mathtt{j}\) plus the length of the edge \(\texttt{u.next[r]}\) is less than \(\mathtt{i}\). Otherwise, we go down into \(L_{\mathtt{r}-1}\).
Node findPred(int i) {
Node u = sentinel;
int r = h;
int j = -1; // index of the current node in list 0
while (r >= 0) {
while (u.next[r] != null && j + u.length[r] < i) {
j += u.length[r];
u = u.next[r];
}
r--;
}
return u;
}
T get(int i) {
if (i < 0 || i > n-1) throw new IndexOutOfBoundsException();
return findPred(i).next[0].x;
}
T set(int i, T x) {
if (i < 0 || i > n-1) throw new IndexOutOfBoundsException();
Node u = findPred(i).next[0];
T y = u.x;
u.x = x;
return y;
}
Since the hardest part of the operations \(\mathtt{get(i)}\) and \(\mathtt{set(i,x)}\) is finding the \(\mathtt{i}\)th node in \(L_0\), these operations run in \(O(\log \mathtt{n})\) time.
Adding an element to a SkiplistList at a position, \(\mathtt{i}\), is fairly simple. Unlike in a SkiplistSSet, we are sure that a new node will actually be added, so we can do the addition at the same time as we search for the new node's location. We first pick the height, \(\mathtt{k}\), of the newly inserted node, \(\mathtt{w}\), and then follow the search path for \(\mathtt{i}\). Any time the search path moves down from \(L_{\mathtt{r}}\) with \(\mathtt{r}\le \mathtt{k}\), we splice \(\mathtt{w}\) into \(L_{\mathtt{r}}\). The only extra care needed is to ensure that the lengths of edges are updated properly. See Figure \(\PageIndex{2}\).
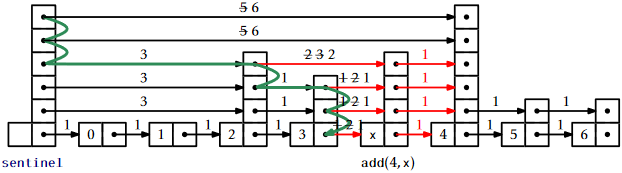
Note that, each time the search path goes down at a node, \(\mathtt{u}\), in \(L_{\mathtt{r}}\), the length of the edge \(\texttt{u.next[r]}\) increases by one, since we are adding an element below that edge at position \(\mathtt{i}\). Splicing the node \(\mathtt{w}\) between two nodes, \(\mathtt{u}\) and \(\mathtt{z}\), works as shown in Figure \(\PageIndex{3}\). While following the search path we are already keeping track of the position, \(\mathtt{j}\), of \(\mathtt{u}\) in \(L_0\). Therefore, we know that the length of the edge from \(\mathtt{u}\) to \(\mathtt{w}\) is \(\mathtt{i}-\mathtt{j}\). We can also deduce the length of the edge from \(\mathtt{w}\) to \(\mathtt{z}\) from the length, \(\ell\), of the edge from \(\mathtt{u}\) to \(\mathtt{z}\). Therefore, we can splice in \(\mathtt{w}\) and update the lengths of the edges in constant time.

This sounds more complicated than it is, for the code is actually quite simple:
void add(int i, T x) {
if (i < 0 || i > n) throw new IndexOutOfBoundsException();
Node w = new Node(x, pickHeight());
if (w.height() > h)
h = w.height();
add(i, w);
}
Node add(int i, Node w) {
Node u = sentinel;
int k = w.height();
int r = h;
int j = -1; // index of u
while (r >= 0) {
while (u.next[r] != null && j+u.length[r] < i) {
j += u.length[r];
u = u.next[r];
}
u.length[r]++; // accounts for new node in list 0
if (r <= k) {
w.next[r] = u.next[r];
u.next[r] = w;
w.length[r] = u.length[r] - (i - j);
u.length[r] = i - j;
}
r--;
}
n++;
return u;
}
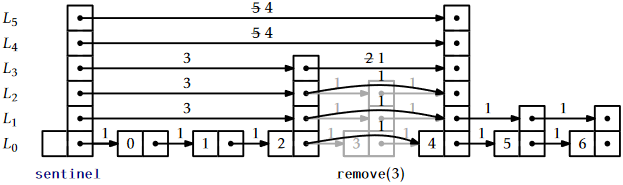
By now, the implementation of the \(\mathtt{remove(i)}\) operation in a SkiplistList should be obvious. We follow the search path for the node at position \(\mathtt{i}\). Each time the search path takes a step down from a node, \(\mathtt{u}\), at level \(\mathtt{r}\) we decrement the length of the edge leaving \(\mathtt{u}\) at that level. We also check if \(\texttt{u.next[r]}\) is the element of rank \(\mathtt{i}\) and, if so, splice it out of the list at that level. An example is shown in Figure \(\PageIndex{4}\).
T remove(int i) {
if (i < 0 || i > n-1) throw new IndexOutOfBoundsException();
T x = null;
Node u = sentinel;
int r = h;
int j = -1; // index of node u
while (r >= 0) {
while (u.next[r] != null && j+u.length[r] < i) {
j += u.length[r];
u = u.next[r];
}
u.length[r]--; // for the node we are removing
if (j + u.length[r] + 1 == i && u.next[r] != null) {
x = u.next[r].x;
u.length[r] += u.next[r].length[r];
u.next[r] = u.next[r].next[r];
if (u == sentinel && u.next[r] == null)
h--;
}
r--;
}
n--;
return x;
}
\(\PageIndex{1}\) Summary
The following theorem summarizes the performance of the SkiplistList data structure:


