4.2: SkiplistSSet - An Efficient SSet

A SkiplistSSet uses a skiplist structure to implement the SSet interface. When used in this way, the list \(L_0\) stores the elements of the SSet in sorted order. The \(\mathtt{find(x)}\) method works by following the search path for the smallest value \(\mathtt{y}\) such that \(\mathtt{y}\ge\mathtt{x}\):

    Node<T> findPredNode(T x) {
        Node<T> u = sentinel;
        int r = h;
        while (r >= 0) {
            while (u.next[r] != null && compare(u.next[r].x,x) < 0)
                u = u.next[r];   // go right in list r
            r--;               // go down into list r-1
        }
        return u;
    }
    T find(T x) {
        Node<T> u = findPredNode(x);
        return u.next[0] == null ? null : u.next[0].x;
    }

Following the search path for \(\mathtt{y}\) is easy: when situated at some node, \(\mathtt{u}\), in \(L_{\mathtt{r}}\), we look right to \(\texttt{u.next[r].x}\). If \(\mathtt{x}>\texttt{u.next[r].x}\), then we take a step to the right in \(L_{\mathtt{r}}\); otherwise, we move down into \(L_{\mathtt{r}-1}\). Each step (right or down) in this search takes only constant time; thus, by Lemma 4.1.1, the expected running time of \(\mathtt{find(x)}\) is \(O(\log \mathtt{n})\).

Before we can add an element to a SkipListSSet, we need a method to simulate tossing coins to determine the height, \(\mathtt{k}\), of a new node. We do so by picking a random integer, \(\mathtt{z}\), and counting the number of trailing \(1\)s in the binary representation of \(\mathtt{z}\):¹

    int pickHeight() {
        int z = rand.nextInt();
        int k = 0;
        int m = 1;
        while ((z & m) != 0) {
            k++;
            m <<= 1;
        }
        return k;
    }

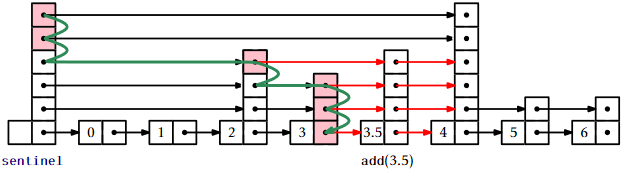
To implement the \(\mathtt{add(x)}\) method in a SkiplistSSet we search for \(\mathtt{x}\) and then splice \(\mathtt{x}\) into a few lists \(L_0\),..., \(L_{\mathtt{k}}\), where \(\mathtt{k}\) is selected using the \(\mathtt{pickHeight()}\) method. The easiest way to do this is to use an array, \(\mathtt{stack}\), that keeps track of the nodes at which the search path goes down from some list \(L_{\mathtt{r}}\) into \(L_{\mathtt{r}-1}\). More precisely, \(\mathtt{stack[r]}\) is the node in \(L_{\mathtt{r}}\) where the search path proceeded down into \(L_{\mathtt{r}-1}\). The nodes that we modify to insert \(\mathtt{x}\) are precisely the nodes \(\mathtt{stack[0]},\ldots,\mathtt{stack[k]}\). The following code implements this algorithm for \(\mathtt{add(x)}\):

    boolean add(T x) {
        Node<T> u = sentinel;
        int r = h;
        int comp = 0;
        while (r >= 0) {
            while (u.next[r] != null 
                   && (comp = compare(u.next[r].x,x)) < 0)
                u = u.next[r];
            if (u.next[r] != null && comp == 0) return false;
            stack[r--] = u;          // going down, store u
        }
        Node<T> w = new Node<T>(x, pickHeight());
        while (h < w.height())
            stack[++h] = sentinel;   // height increased
        for (int i = 0; i < w.next.length; i++) {
            w.next[i] = stack[i].next[i];
            stack[i].next[i] = w;
        }
        n++;
        return true;
    }

Figure \(\PageIndex{1}\): Adding the node containing \(3.5\) to a skiplist. The nodes stored in \(\mathtt{stack}\) are highlighted.

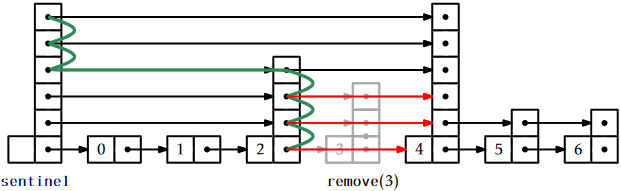
Removing an element, \(\mathtt{x}\), is done in a similar way, except that there is no need for \(\mathtt{stack}\) to keep track of the search path. The removal can be done as we are following the search path. We search for \(\mathtt{x}\) and each time the search moves downward from a node \(\mathtt{u}\), we check if \(\texttt{u.next.x}=\mathtt{x}\) and if so, we splice \(\mathtt{u}\) out of the list:

    boolean remove(T x) {
        boolean removed = false;
        Node<T> u = sentinel;
        int r = h;
        int comp = 0;
        while (r >= 0) {
            while (u.next[r] != null 
                   && (comp = compare(u.next[r].x, x)) < 0) {
                u = u.next[r];
            }
            if (u.next[r] != null && comp == 0) {
                removed = true;
                u.next[r] = u.next[r].next[r];
                if (u == sentinel && u.next[r] == null)
                    h--;  // height has gone down
            }
            r--;
        }
        if (removed) n--;
        return removed;
    }

Figure \(\PageIndex{2}\): Removing the node containing \(3\) from a skiplist.

\(\PageIndex{1}\) Summary

The following theorem summarizes the performance of skiplists when used to implement sorted sets:

Theorem \(\PageIndex{1}\).

SkiplistSSet implements the SSet interface. A SkiplistSSet supports the operations \(\mathtt{add(x)}\), \(\mathtt{remove(x)}\), and \(\mathtt{find(x)}\) in \(O(\log \mathtt{n})\) expected time per operation.

---

Footnotes

¹This method does not exactly replicate the coin-tossing experiment since the value of \(\mathtt{k}\) will always be less than the number of bits in an \(\mathtt{int}\). However, this will have negligible impact unless the number of elements in the structure is much greater than \(2^{32}=4294967296\).