3.6: Address translation
- Page ID
- 40723
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)How does a virtual address (VA) get translated to a physical address (PA)? The basic mechanism is simple, but a simple implementation would be too slow and take too much space. So actual implementations are a bit more complicated.
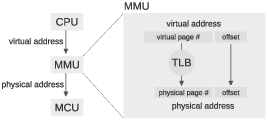
Most processors provide a memory management unit (MMU) that sits between the CPU and main memory. The MMU performs fast translation between VAs and PAs.
- When a program reads or writes a variable, the CPU generates a VA.
- The MMU splits the VA into two parts, called the page number and the offset. A “page” is a chunk of memory; the size of a page depends on the operating system and the hardware, but common sizes are 1–4 KiB.
- The MMU looks up the page number in the translation lookaside buffer (TLB) and gets the corresponding physical page number. Then it combines the physical page number with the offset to produce a PA.
- The PA is passed to main memory, which reads or writes the given location.
The TLB contains cached copies of data from the page table (which is stored in kernel memory). The page table contains the mapping from virtual page numbers to physical page numbers. Since each process has its own page table, the TLB has to make sure it only uses entries from the page table of the process that’s running.
Figure \(\PageIndex{1}\) shows a diagram of this process. To see how it all works, suppose that the VA is 32 bits and the physical memory is 1 GiB, divided into 1 KiB pages.
- Since 1 GiB is \( 2^{30} \)bytes and 1 KiB is \( 2^{10} \)bytes, there are \( 2^{20} \) physical pages, sometimes called “frames.”
- The size of the virtual address space is \(2^{32} \) B and the size of a page is \( 2^{10} \) B, so there are \( 2^{22} \) virtual pages.
- The size of the offset is determined by the page size. In this example the page size is \( 2^{10} \) B, so it takes 10 bits to specify a byte on a page.
- If a VA is 32 bits and the offset is 10 bits, the remaining 22 bits make up the virtual page number.
- Since there are \( 2^{20} \) physical pages, each physical page number is 20 bits. Adding in the 10 bit offset, the resulting PAs are 30 bits.
So far this all seems feasible. But let’s think about how big a page table might have to be. The simplest implementation of a page table is an array with one entry for each virtual page. Each entry would contain a physical page number, which is 20 bits in this example, plus some additional information about each frame. So we expect 3–4 bytes per entry. But with 222 virtual pages, the page table would require 224 bytes, or 16 MiB.
And since we need a page table for each process, a system running 256 processes would need \( 2^{32} \) bytes, or 4 GiB, just for page tables! And that’s just with 32-bit virtual addresses. With 48- or 64-bit VAs, the numbers are ridiculous.
Fortunately, we don’t actually need that much space, because most processes don’t use even a small fraction of their virtual address space. And if a process doesn’t use a virtual page, we don’t need an entry in the page table for it.
Another way to say the same thing is that page tables are “sparse”, which implies that the simple implementation, an array of page table entries, is a bad idea. Fortunately, there are several good implementations for sparse arrays.
One option is a multilevel page table, which is what many operating systems, including Linux, use. Another option is an associative table, where each entry includes both the virtual page number and the physical page number. Searching an associative table can be slow in software, but in hardware we can search the entire table in parallel, so associative arrays are often used to represent the page table entries in the TLB.
You can read more about these implementations at http://en.Wikipedia.org/wiki/Page_table; you might find the details interesting. But the fundamental idea is that page tables are sparse, so we have to choose a good implementation for sparse arrays.
I mentioned earlier that the operating system can interrupt a running process, save its state, and then run another process. This mechanism is called a context switch. Since each process has its own page table, the operating system has to work with the MMU to make sure each process gets the right page table. In older machines, the page table information in the MMU had to be replaced during every context switch, which was expensive. In newer systems, each page table entry in the MMU includes the process ID, so page tables from multiple processes can be in the MMU at the same time.


