17.5: PetitParser Browser

PetitParser is shipped with a powerful browser that can help to develop complex parsers. The PetitParser Browser provides graphical visualization, debugging support, refactoring support, and some other features discussed later in this chapter. You will see that these features could be very useful while developing your own parser. Pay attention to have Glamour already loaded in your system. To load Glamour, see 10. Then to open the PetitParser simply evaluate this expression:

Code \(\PageIndex{1}\) (Pharo): Opening PetitParser browser

PPBrowser open.

PetitParser Browser overview

Figure \(\PageIndex{1}\): PetitParser Browser window.

In Figure \(\PageIndex{1}\) you can see the PPBrowser window. The left panel, named Parsers, contains the list of all parsers in the system. You can see ExpressionGrammar and its subclasses as well as the PPJsonGrammar that we defined earlier in this chapter. Selecting one of the parsers in this pane activates the upper-right side of the browser. For each rule of the selected parser (e.g., prim) you can see 5 tabs related to the rule.

Source shows the source code of the rule. The code can be updated and saved in this window. Moreover, you can add a new rule simply by defining the new method name and body.

Graph shows the graphical representation of the rule. It is updated as the rule source is changed. You can see the prim visual representation in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): Graph visualization of the prim rule.

Example shows an automatically generated example based on the definition of the rule (see Figure \(\PageIndex{3}\) for an example for the prim rule). In the top-right corner, the reload button generates a new example for the same rule (see Figure \(\PageIndex{4}\) for another automatically generated example of the prim rule, this time with a parenthesized expression).

Figure \(\PageIndex{3}\): An automatically generated example of the prim rule. In this case, the prim example is a number.

Figure \(\PageIndex{4}\): Another automatically generated example of the prim rule, after having clicked the reload button. In this case, the prim example is a parenthesized expression.

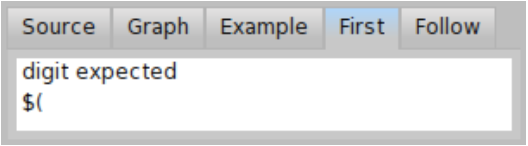
First shows set of terminal parsers that can be activated directly after the rule started. As you can see on Figure \(\PageIndex{5}\), the first set of prim is either digit or opening parenthesis '('. This means that once you start parsing prim the input should continue with either digit or '('.

One can use first set to double-check that the grammar is specified correctly. For example, if you see '+' in the first set of prim, there is something wrong with the definitions, because the prim rule was never ment to start with binary operator.

Terminal parser is a parser that does not delegate to any other parser. Therefore you don’t see parens in prim first set because parens delegates to another parsers – trimming and sequence parsers (see Code \(\PageIndex{2}\)). You can see '(' which is first set of parens. The same states for number rule which creates action parser delegating to trimming parser delegating to flattening parser delegating to repeating parser delegating to #digit parser (see Code \(\PageIndex{2}\)). The #digit parser is terminal parser and therefore you can see ’digit expected’ in a first set. In general, computation of first set could be complex and therefore PPBrowser computes this information for us.

Figure \(\PageIndex{5}\): The first set of the prim rule.

Code \(\PageIndex{2}\) (Python): prim rule in ExpressionGrammar

ExpressionGrammar>>prim
    ^ parens / number

ExpressionGrammar>>parens
    ^ $( asParser trim, term, $} asParser trim

ExpressionGrammar>>number
    ^ #digit asParser plus flatten trim ==> [:str | str asNumber ]

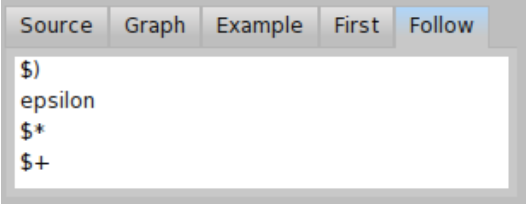
Follow shows set of terminal parsers that can be activated directly after the rule finished. As you can see on Figure \(\PageIndex{6}\), the follow set of prim is closing bracket character parser ')', star character parser '*', plus character parser '+' or epsilon parser (which states for empty string). In other words, once you finished parsing prim rule the input should continue with one of ')', '*', '+' characters or the input should be completely consumed.

One can use follow set to double-check that the grammar is specified correctly. For example if you see '(' in prim follow set, something is wrong in the definition of your grammar. The prim rule should be followed by binary operator or closing bracket, not by opening bracket.

In general, computation of follow could be even more complex than computation of first and therefore PPBrowser computes this information for us.

Figure \(\PageIndex{6}\): The follow set of the prim rule.

The lower-right side of the browser is related to a particular parsing input. You can specify an input sample by filling in the text area in the Sample tab. One may parse the input sample by clicking the play button or by pressing Cmd-s or Ctrl-s. You can then gain some insight on the parse result by inspecting the tabs on the bottom-right pane:

Result shows the result of parsing the input sample that can be inspected by clicking either the Inspect or Explore buttons. Figure \(\PageIndex{7}\) shows the result of parsing (1+2).

Figure \(\PageIndex{7}\): Result of parsing the (1+2) sample expression.

Debugger shows a tree view of the steps that were performed during parsing. This is very useful if you don’t know what exactly is happening during parsing. By selecting the step the subset of input is highlighted, so you can see which part of input was parsed by a particular step.

For example, you can inspect how the ExpressionGrammar works, what rules are called and in which order. This is depicted in Figure \(\PageIndex{8}\). The grey rules are rules that failed. This usually happens for choice parsers and you can see an example for the prod rule (the definition is in Code \(\PageIndex{3}\)). When parser was parsing \( 12 + 3 * 4 \) term, the parser tried to parse mul rule as a first option in prod. But mul required star character '*' at position 2 which is not present, so that the mul failed and instead the prim with value 12 was parsed.

Code \(\PageIndex{3}\) (Pharo): prod rule in ExpressionGrammar

ExpressionGrammar>>prod
    ^ mul / prim

ExpressionGrammar>>mul
    ^ prim, $* asParser trim, prod

Compare what happens during parsing when we change from \( 12 + 3 * 4 \) to \( 12 * 3 * 4 \). What rules are applied know, which of them fails? The second debugger output is in Figure \(\PageIndex{9}\), but give it your own try.

Figure \(\PageIndex{8}\): Debugger output of ExpressionGrammar for input \( 12 + 3 * 4 \).

Figure \(\PageIndex{9}\): Debugger output of ExpressionGrammar for input \( 12 * 3 * 4 \).

Tally shows how many times a particular parser got called during the parsing. The percentage shows the number of calls to total number of calls ratio. This might be useful while optimizing performance of your parser (see Figure \(\PageIndex{10}\)).

Profile shows how much time was spent in particular parser during parsing of the input. The percentage shows the ratio of time to total time. This might be useful while optimizing performance of your parser (see Figure \(\PageIndex{11}\)).

Progress visually shows how a parser consumes input. The x-axis represents how many characters were read in the input sample, ranging from 0 (left margin) to the number of characters in the input (right margin). The y-axis represents time, ranging from the beginning of the parsing process (top margin) to its end (bottom margin). A line going from top-left to bottom-right (such as the one in Figure \(\PageIndex{12}\)) shows that the parser completed its task by only reading each character of the input sample once. This is the best case scenario, parsing is linear in the length of the input: In another words, input of \( n \) characters is parsed in \( n \) steps.

Figure \(\PageIndex{10}\): Tally of ExpressionGrammar for input \( 12 * 3 * 4 \).

Figure \(\PageIndex{11}\): Profile of ExpressionGrammar for input \( 12 * 3 * 4 \).

Figure \(\PageIndex{12}\): Progress of Petit Parser that parses input in linear amount of steps.

When multiple lines are visible, it means that the parser had to go back to a previously read character in the input sample to try a different rule. This can be seen in Figure \(\PageIndex{13}\). In this example, the parser had to go back several times to correctly parse the whole input sample: all input was parsed in \( n! \) steps which is very bad. If you see many backward jumps for a grammar, you should reconsider the order of choice parsers, restructure your grammar or use a memoized parser. We will have a detailed look on a backtracking issue in the following section.

Figure \(\PageIndex{13}\): Progress of Petit Parser with a lot of backtracking.

Debugging example

As an exercise, we will try to improve a BacktrackingParser from Code \(\PageIndex{4}\). The BacktrackingParser was designed to accept input corresponding to the regular expressions 'a*b' and 'a*c'. The parser gives us correct results, but there is a problem with performance. The BacktrackingParser does too much backtracking.

Code \(\PageIndex{4}\) (Pharo): A parser accepting 'a*b' and 'a*c' with too much backtracking

PPCompositeParser subclass: #BacktrackingParser
    instanceVariableNames: 'ab ap c p'
    classVariableNames: ''
    poolDictionaries: ''
    category: 'PetitTutorial'

BacktrackingParser>>ab
    ^ 'b' asParser /
      ('a' asParser, ab)

BacktrackingParser>>c
    ^ 'c' asParser

BacktrackingParser>>p
    ^ ab / ap / c

BacktrackingParser>>start
    ^p

BacktrackingParser>>ap
    ^ 'a' asParser, p

Let us get some overview to better understand, what is happening. First of all, try to parse \( \mathit{input}_{b} = \) 'aaaaaaaaab' and \( \mathit{input}_{c} = \) 'aaaaaaaaac'. As we can see from progress depicted in Figure \(\PageIndex{14}\), the \( \mathit{input}_{b} \) is parsed in more or less linear time and there is no backtracking. But the progress depicted in Figure \(\PageIndex{15} \) looks bad. The \( \mathit{input}_{c} \) is parsed with a lot of backtracking and in much more time. We can even compare the tally output for both inputs \( \mathit{input}_{b} \) and \( \mathit{input}_{c} \) (see Figure \(PageIndex{16} \) and Figure \(\PageIndex{17}\)). In case of \( \mathit{input}_{b} \), the total invocation count of the parser b is 19 and invocation count of the parser a is 9. It is much less than 110 invocations for the parser b and 55 invocations for the parser a in case of \( \mathit{input}_{c} \).

Figure \(\PageIndex{14}\): Progress of the BacktrackingParser for \( \mathit{input}_{b} \).

Figure \(\PageIndex{15}\): Progress of the BacktrackingParser for \( \mathit{input}_{c} \).

Figure \(\PageIndex{16}\): Tally output of the BacktrackingParser for \( \mathit{input}_{b} \).

Figure \(\PageIndex{17}\): Tally output of the BacktrackingParser for \( \mathit{input}_{c} \).

We can see there is some problem with \( \mathit{input}_{c} \). If we still don’t know what is the problem, the debugger window might give us more hints. Let us have a look at the debugger window for \( \mathit{input}_{b} \) as depicted in Figure \(\PageIndex{18}\). We can see that in each step, one 'a' is consumed and the parser ab is invoked until it reaches the 'b'. The debugger window for \( \mathit{input}_{c} \) as depicted in Figure \(\PageIndex{19}\) looks much different. There is a progress within the p -> ab -> ap -> p loop but the parser ab fails in each repetition of the loop. Since the parser ab fails after having read all the string to the end and seen 'c' instead of 'b', we have localized the cause of the backtracking. We know the problem now, so what can we do? We may try to update BacktrackingParser so that the 'a*c' strings are parsed in a similar way as the 'a*b' strings. You can see such a modification in Code \(\PageIndex{5}\).

Code \(\PageIndex{5}\) (Pharo): A slightly better parser accepting 'a*b' and 'a*c'.

PPCompositeParser subclass: #BacktrackingParser
    instanceVariableNames: 'ab ac'
    classVariableNames: ''
    poolDictionaries: ''
    category: 'PetitTutorial'

BacktrackingParser>>ab
    ^ 'b' asParser /
      ('a' asParser, ab)

BacktrackingParser>>ac
    ^ 'c' asParser /
      ('a' asParser, ac)

BacktrackingParser>>start
    ^ ab / ac

Figure \(\PageIndex{18}\): Debugging output of BacktrackingParser for \( \mathit{input}_{b} \).

Figure \(\PageIndex{19}\): Debugging output of BacktrackingParser for \( \mathit{input}_{c} \).

We can check the new metrics for \( \mathit{input}_{c} \) in both Figure \(\PageIndex{20}\) and Figure \(\PageIndex{21}\). There is significant improvement. For \( \mathit{input}_{c} \), the tally shows only 20 invocations of the parser b and 9 invocations of the parser a. This is very good improvement compared to the 110 invocations of the parser b and 55 invocations of the parser a in the original version of BacktrackingParser (see Figure \(\PageIndex{17}\)).

Figure \(\PageIndex{20}\): Progress of BacktrackingParser for \( \mathit{input}_{c} \) after the first update.

Figure \(\PageIndex{21}\): Tally of BacktrackingParser for \( \mathit{input}_{c} \) after the first update.

Yet, we might try to do even better. There is still one backtracking happening for \( \mathit{input}_{c} \). It happens when the parser ab tries to recognize the 'a*b' input and fails (and backtracks) so that the parser ac can recognize the 'a*c' input. What if we try to consume all the 'a's and then we choose between 'b' and 'c' at the very end? You can see such a modification of the BacktrackingParser in Code \(\PageIndex{6}\). In that case, we can see the progress without any backtracking even for \( \mathit{input}_{c} \) as depicted in Figure \(\PageIndex{22}\).

Figure \(\PageIndex{22}\): Progress of the BacktrackingParser after the second update for \( \mathit{input}_{c} \).

Figure \(\PageIndex{23}\): Tally of the BacktrackingParser after the second update for \( \mathit{input}_{c} \).

On the other hand, the number of parser invocations for \( \mathit{input}_{b} \) increased by 18 (the Table \(\PageIndex{1}\) summarizes the total number of invocations for each version of the BacktrackingParser). It is up to the developer to decide which grammar is more suitable for his needs. It is better to use the second improved version in case 'a*b' and 'a*c' occur with the same probability in the input. If we expect more 'a*b' strings in the input, the first version is better.

Code \(\PageIndex{6}\) (Pharo): An even better parser accepting 'a*b' and 'a*c'.

PPCompositeParser subclass: #BacktrackingParser
    instanceVariableNames: 'abc'
    classVariableNames: ''
    poolDictionaries: ''
    category: 'PetitTutorial'

BacktrackingParser>>abc
    ^ ('b' asParser / 'c' asParser) /
      ('a' asParser, abc)

BacktrackingParser>>start
    ^ abc

Table \(\PageIndex{1}\): Number of parser invocations for \( \mathit{input}_{b} \) and \( \mathit{input}_{c} \) depending on the version of BacktrackingParser.

	# of invocations
Version	\( \mathit{input}_{b} \)	\( \mathit{input}_{c} \)
Original	28	233
First improvement	28	70
Second improvement	46	48