3.5: Division in MIPS Assembly

Division, like multiplication requires two registers to produce an answer. The reason for this has to do with how the hardware calculates the result, and is harder to explain without considering the hardware used, which is beyond the scope of this textbook. The reader is thus asked to just believe that two registers are needed, and that MIPS will again use the registers hi and lo.

To understand division, we will again begin with a base 10 example. Remember how division was done when it was introduced to you in elementary school. The result of 17 divided by 5 would be the following:

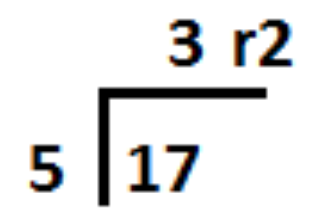
In this equation, the value 5 is called the divisor, the 17 is the dividend, 3 is the quotient, and 2 is the remainder.

In MIPS, when integer division is done, the lo register will contain the quotient, and the hi register will contain the remainder. This means that in MIPS integer arithmetic when the quotient is taken from the low register the results will be truncated. If the programmer wants to round the number, this can be implemented using the remainder (see problems at the end of Chapter 5).

Now that the fundamentals of integer division have been covered, there are two MIPS division operators that will be looked at. They are:

• div operator, which has 3 formats. The first format is the only real format of this operator. The operator divides R_s by R_t and stores the result in the [hi,lo] register pair with the quotient in the lo and the remainder in the hi. The format and meaning of this operator is:

  format:	div Rs, Rt
  meaning:	[hi,lo] <- Rs / Rt

  The second format of the div operator is a pseudo instruction. It is a 3 address format, but is still a pseudo instruction. In addition to executing a division instruction, this pseudo instruction also checks for a zero divide. The specifics of the check will not be covered at this point as it involves bne and break instructions. The format, meaning, and translation of the pseudo operators is as follows:

  format:	div Rd, Rs, Rt
  meaning:	[if Rt !=0] Rd <-Rs / Rt else break
  translation:	bne Rt, $zero, 0x00000001 break div Rs, Rt mflo Rd

  The third format of the div operator is a pseudo instruction. The format, meaning, and translation of the pseudo operators is as follows:

  format:	div Rd, Rs, Immediate
  meaning:	Rd <- Rs / Immediate
  translation:	addi $Rt, $zero, Immediate div Rs, Rt mflo Rd

• rem (remainder) operator, which has 2 formats. There are only pseudo formats for this instruction. The first format of the rem operator is a pseudo instruction. The format, meaning, and translation of the pseudo operators is as follows:

  format:	div Rd, Rs, Rt
  meaning:	[if Rt !=0] Rd <-Rs % Rt else break
  translation:	bne Rt, $zero, 0x00000001 break div Rs, Rt mfhi Rd

  The second format of the rem operator is also a pseudo instruction. The format, meaning, and translation of the pseudo operators is as follows:

  format:	rem Rd, Rs, Immediate
  meaning:	Rd <- Rs / Immediate
  translation:	addi $Rt, $zero, Immediate div Rs, Rt mfhi Rd

3.5.1 Remainder operator, even/odd number checker

Some students question the usefulness of the remainder operator, but a number of interesting algorithms are based on it. For example, this section presents a short program which checks if a number is odd or even. Note that since branching has not yet been covered, this program will print out a 0 if the number is even, and 1 if the number is odd. Because branching has not yet been covered, the program will print out 0 if the number is even, and 1 if it is odd.

The algorithm checks the remainder of a division by 2. If the number is evenly divisible by 2, the remainder will be 0 and the number is even. If the number is not evenly divisible by 2, the remainder is 1 and the number is odd. The pseudo code for this algorithm uses the "%" or modulus operator to obtain the remainder.

main
{
    int i = prompt("Enter your number");
    int j = i % 2;
    print("A result of 0 is even, a result of 1 is odd: result = " + j;
}

3.5.2 Remainder operator, even/odd number checker

The following is the MIPS implementation of the even/odd checker. To find the remainder the div operator is used to divide by 2 and the remainder retrieved from the hi register. If the remainder is 0 the number is even, and 1 if it is odd.

Program 3-2: Even/odd number checking program

# File:        Program3-3.asm
# Author:      Charles W. Kann
# Purpose:     To have a user enter a number,and print 0 if the number is even, 1 if the number is odd
.text
.globl main
main:
    # Get input value
    addi $v0, $zero, 4    # Write Prompt
    la $a0, prompt
    syscall
    addi $v0, $zero, 5    # Retrieve input
    syscall
    move $s0, $v0
    
    # Check if odd or even
    addi $t0, $zero, 2    # Store 2 in $t0
    div $t0, $s0, $t0     # Divide input by 2
    mfhi $s1              # Save remainder in $s1
    
    # Print output        
    addi $v0, $zero, 4    # Print result string
    la $a0, result
    syscall
    addi $v0, $zero, 1    # Print result
    move $a0, $s1
    syscall
    
    #Exit program
    addi $v0, $zero, 10
    syscall
.data
prompt: .asciiz "Enter your number: "
result: .asciiz "A result of 0 is even, 1 is odd: result = "