16.3: The Stack ADT

A stack is a special type of list that allows insertions and removals to be performed only to the front of the list. Therefore, it enforces last-in–firstout (LIFO) behavior on the list. Think of a stack of dishes at the salad bar. When you put a dish on the stack, it goes onto the top of the stack. When you remove a dish from the stack, it comes from the top of the stack (Fig. 16.20).

The stack operations are conventionally called push, for insert, and pop, for remove, respectively. Thus, the stack ADT stores a list of data and supports the following operations:

• Push—inserts an object onto the top of the stack.
• Pop—removes the top object from the stack.
• Empty—returns true if the stack is empty.
• Peek—retrieves the top object without removing it.

Stack applications

Stacks are useful for a number of important computing tasks. For example, during program execution, method call and return happens in a LIFO fashion. The last method called is the first method exited. Therefore, a stack structure known as the run-time stack is used to manage method calls during program execution. When a method is called, an activation block is created, which includes the method’s parameters, local variables, and return address. The activation block is pushed onto the stack. When that method call returns, the return address is retrieved from the activation block and the whole block is popped off the stack. The Exception.printStackTrace() method uses the run-time stack to print a trace of the method calls that led to an exception.

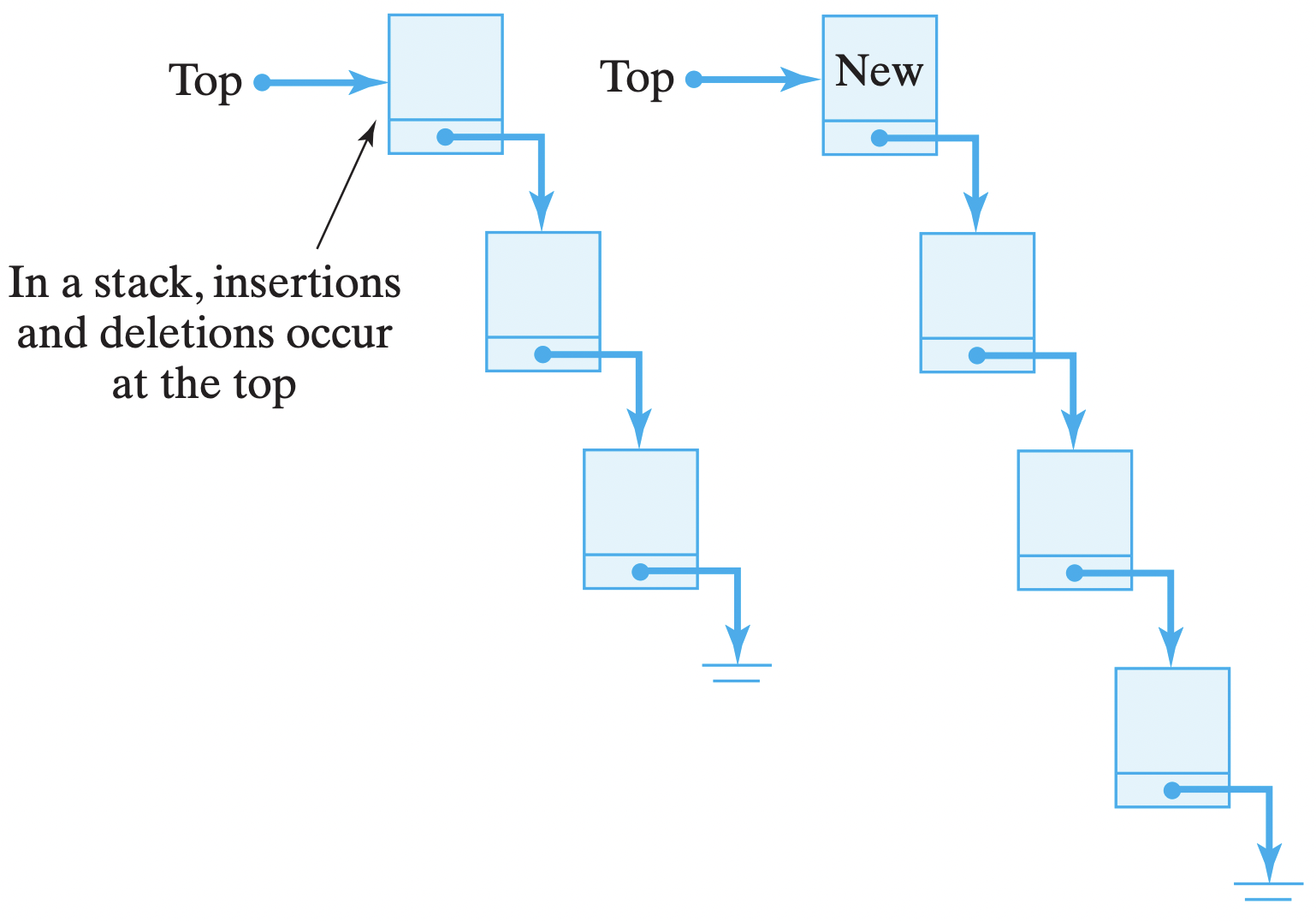Figure 16.20: A stack is a list that permits insertions and removals only at its top.

16.3.1 The Stack Class

Given our general definition of List and Node, it is practically trivial to define the stack ADT as a subclass of List (Fig. 16–21). As a subclass of List, a Stack will inherit all of the public and protected methods defined in List. Therefore, we can simply use the insertAtFront() and removeFirst() methods for the push and pop operations, respectively (Fig. 16.22). Because the isEmpty() method is defined in List, there’s  no need to override it in Stack. In effect, the push() and pop() methods merely rename the insertAtFront() and removeFirst() methods. Note that the Stack() constructor calls the superclass constructor. This is necessary so that the list can be initialized.

Figure 16.21: As a subclass of List, a Stack inherits all of its public (+) and protected (#) elements. Therefore, push() can be defined in terms of insertAtFront() and pop() can be defined in terms of removeFirst().

Figure 16.22: The Stack ADT.

Do we have to make any changes to the List class in order to use it this way? Yes. We want to change the declaration of head from private to protected, so it can be accessed in the Stack class. And we want to declare List’s public access methods, such as insertAtFront() and removeFirst(), as protected. That will allow them to be used in Stack, and in any classes that extend List, but not by other classes. This is essential. Unless we do this we haven’t really restricted the stack operations to push and pop and, therefore, we haven’t really defined a stack ADT. Remember, an ADT defines the data and the operations on the data. A stack ADT must restrict access to the data to just the push and pop operations.

JAVA LANGUAGE RULE

Protected Elements.

An object’s protected elements are hidden from all other objects except instances of the same class or its subclasses.

JAVA EFFECTIVE DESIGN

Information Hiding.

Use the private and protected qualifiers to hide an ADT’s implementation details from other objects. Use public to define the ADT’s interface.

SELF-STUDY EXERCISE

Exercise 16.9

Define the peek() method for the Stack class. It should take no parameters and return an Object. It should return the Object on the top of the stack.

16.3.2 Testing the Stack Class

Reversing a string

Now let’s test our stack class by using a stack to reverse the letters in a String. The algorithm is this: Starting at the front of the String, push each letter onto the stack until you reach the end of the String. Then pop letters off the stack and concatenate them, left to right, into another String, until the stack is empty (Fig. 16.23).

Note that because our Nodes store Objects, we must convert each char into a Character, using the wrapper class. Note also that we can use the toString() method to convert from Object to String as we are popping the stack.