8.3: Exercise 6
- Page ID
- 12773
In the repository for this book, you’ll find the source files for this exercise:
- TermCounter.java contains the code from the previous section.
- TermCounterTest.java contains test code for TermCounter.java.
- Index.java contains the class definition for the next part of this exercise.
- WikiFetcher.java contains the class we used in the previous exercise to download and parse Web pages.
- WikiNodeIterable.java contains the class we used to traverse the nodes in a DOM tree.
You’ll also find the Ant build file build.xml.
Run ant build to compile the source files. Then run ant TermCounter; it should run the code from the previous section and print a list of terms and their counts. The output should look something like this:
genericservlet, 2 configurations, 1 claimed, 1 servletresponse, 2 occur, 2 Total of all counts = -1
When you run it, the order of the terms might be different.
The last line is supposed to print the total of the term counts, but it returns -1 because the method size is incomplete. Fill in this method and run ant TermCounter again. The result should be 4798.
Run ant TermCounterTest to confirm that this part of the exercise is complete and correct.
For the second part of the exercise, I’ll present an implementation of an Index object and you will fill in a missing method. Here’s the beginning of the class definition:
public class Index {
private Map<String, Set<TermCounter>> index = new HashMap<String, Set<TermCounter>>();
public void add(String term, TermCounter tc) {
Set<TermCounter> set = get(term);
// if we’re seeing a term for the first time, make a new Set
if (set == null) {
set = new HashSet<TermCounter>();
index.put(term, set);
}
// otherwise we can modify an existing Set
set.add(tc);
}
public Set<TermCounter> get(String term) {
return index.get(term);
}
The instance variable, index, is a map from each search term to a set of TermCounter objects. Each TermCounter represents a page where the search term appears.
The add method adds a new TermCounter to the set associated with a term. When we index a term that has not appeared before, we have to create a new set. Otherwise we can just add a new element to an existing set. In that case, set.add modifies a set that lives inside index, but doesn’t modify index itself. The only time we modify index is when we add a new term.
Finally, the get method takes a search term and returns the corresponding set of TermCounter objects.
This data structure is moderately complicated. To review, an Index contains a Map from each search term to a Set of TermCounter objects, and each TermCounter is a map from search terms to counts.
Figure \(\PageIndex{1}\) is an object diagram that shows these objects. The Index object has an instance variable named index that refers to a Map. In this example the Map contains only one string, "Java", which maps to a Set that contains two TermCounter objects, one for each page where the word “Java” appears.
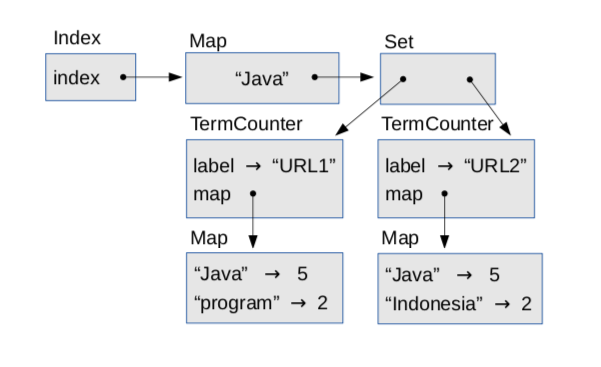
Figure \(\PageIndex{1}\): Object diagram of an Index.
Each TermCounter contains label, which is the URL of the page, and map, which is a Map that contains the words on the page and the number of times each word appears.
The method printIndex shows how to unpack this data structure:
public void printIndex() {
// loop through the search terms
for (String term: keySet()) {
System.out.println(term);
// for each term, print pages where it appears and frequencies
Set<TermCounter> tcs = get(term);
for (TermCounter tc: tcs) {
Integer count = tc.get(term);
System.out.println(" " + tc.getLabel() + " " + count);
}
}
}
The outer loop iterates the search terms. The inner loop iterates the TermCounter objects.
Run ant build to make sure your source code is compiled, and then run ant Index. It downloads two Wikipedia pages, indexes them, and prints the results; but when you run it you won’t see any output because we’ve left one of the methods empty.
Your job is to fill in indexPage, which takes a URL (as a String) and an Elements object, and updates the index. The comments below sketch what it should do:
public void indexPage(String url, Elements paragraphs) {
// make a TermCounter and count the terms in the paragraphs
// for each term in the TermCounter, add the TermCounter to the index
}
When it’s working, run ant Index again, and you should see output like this:
...
configurations
http://en.Wikipedia.org/wiki/Programming_language 1
http://en.Wikipedia.org/wiki/Java_(programming_language) 1
claimed
http://en.Wikipedia.org/wiki/Java_(programming_language) 1
servletresponse
http://en.Wikipedia.org/wiki/Java_(programming_language) 2
occur
http://en.Wikipedia.org/wiki/Java_(programming_language) 2
The order of the search terms might be different when you run it.
Also, run ant TestIndex to confirm that this part of the exercise is complete.


