3.1: Integer Representation
- Page ID
- 19869
Representing integer numbers refers to how the computer stores or represents a number in memory. The computer represents numbers in binary (1's and 0's). However, the computer has a limited amount of space that can be used for each number or variable. This directly impacts the size, or range, of the number that can be represented. For example, a byte (8-bits) can be used to represent \(2^{8}\) or 256 different numbers. Those 256 different numbers can be unsigned (all positive) in which case we can represent any number between 0 and 255 (inclusive). If we choose signed (positive and negative values), then we can represent any number between -128 and +127 (inclusive).
If that range is not large enough to handle the intended values, a larger size must be used. For example, a word (16-bits) can be used to represent \(2^{16}\) or 65,536 different values, and a double-word (32-bits) can be used to represent \(2^{32}\) or 4,294,967,296 different numbers. So, if you wanted to store a value of 100,000 then a double-word would be required.
As you may recall from C, C++, or Java, an integer declaration (e.g., int <variable>) is a single double-word which can be used to represent values between \(-2^{31}\) (−2,147,483,648) and +\(2^{31}\) - 1 (+2,147,483,647).
The following table shows the ranges associated with typical sizes:
| Size | Size | Unsigned Range | Signed Range |
|---|---|---|---|
| Bytes (8-bits) | \(2^8\) | 0 to 255 | -128 to + 127 |
| Words (16-bits) | \(2^{16}\) | 0 to 65,535 | -32768 to +32,767 |
| Double-words (32-bits) | \(2^{32}\) | 0 to 4,294,967,295 | -2,147,483,648 to +2,147,483,647 |
| Quadword | \(2^{64}\) | 0 to \(2^{64}\) - 1 | -(\(2^{63}\)) to \(2^{63}\) - 1 |
| Double quadword | \(2^{128}\) | 0 to \(2^{128}\) - 1 | -(\(2^{127}\)) to \(2^{127}\) - 1 |
In order to determine if a value can be represented, you will need to know the size of the storage element (byte, word, double-word, quadword, etc.) being used and if the values are signed or unsigned.
- For representing unsigned values within the range of a given storage size, standard binary is used.
- For representing signed values within the range, two's complement is used. Specifically, the two's complement encoding process applies to the values in the negative range. For values within the positive range, standard binary is used.
For example, the unsigned byte range can be represented using a number line as follows:

For example, the signed byte range can also be represented using a number line as follows:
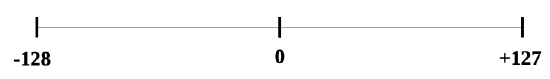
The same concept applies to halfwords and words which have larger ranges.
Since unsigned values have a different, positive only, range than signed values, there is overlap between the values. This can be very confusing when examining variables in memory (with the debugger).
For example, when the unsigned and signed values are within the overlapping positive range (0 to +127):
- A signed byte representation of \(12_{10}\) is 0x0\(C_{16}\)
- An unsigned byte representation of \(-12_{10}\) is also 0x0\(C_{16}\)
When the unsigned and signed values are outside the overlapping range:
- A signed byte representation of \(-15_{10}\) is 0x\(F1_{16}\)
- An unsigned byte representation of \(241_{10}\) is also 0x\(F1_{16}\)
This overlap can cause confusion unless the data types are clearly and correctly defined.
Two's Complement
The following describes how to find the two's complement representation for negative values (not positive values).
To take the two's complement of a number:
- take the one's complement (negate)
- add 1 (in binary)
The same process is used to encode a decimal value into two's complement and from two's complement back to decimal. The following sections provide some examples.
Example
For example, to find the byte size (8-bits), two's complement representation of -9 and - 12.
| 9 (8 + 1) = | 00001001 |
| Step 1 | 11110110 |
| Step 2 | 11110111 |
| -9 (in hex) | F7 |
| 12 (8 + 4) = | 00001100 |
| Step 1 | 11110011 |
| 11110100 | |
| -12 (in hex) | F4 |
Note, all bits for the given size, byte in this example, must be specified.
Example
To find the word size (16-bits), two's complement representation of -18 and -40.
| 18 (16 + 2) = | 0000000000010010 |
| Step 1 | 1111111111101101 |
| Step 2 | 1111111111101110 |
| -18 (hex) | 0xFFEE |
| 40 (32 + 8) = | 0000000000101000 |
| Step 1 | 1111111111010111 |
| Step 2 | 1111111111011000 |
| -40 (hex) | 0xFFD8 |
Note, all bits for the given size, words in these examples, must be specified.


