7.5: Integer Arithmetic Instructions
- Page ID
- 19901
The integer arithmetic instructions perform arithmetic operations such as addition, subtraction, multiplication, and division on integer values. The following sections present the basic integer arithmetic operations.
Addition
The general form of the integer addition instruction is as follows:
add <dest>, <src>
Where operation performs the following:
<dest> = <dest> + <src>
Specifically, the source and destination operands are added and the result is placed in the destination operand (over-writing the previous contents). The value of the source operand is unchanged. The destination and source operand must be of the same size (both bytes, both words, etc.). The destination operand cannot be an immediate. Both operands, cannot be memory. If a memory to memory addition operation is required, two instructions must be used.
For example, assuming the following data declarations:
bNum1 db 42 bNum2 db 73 bAns db 0 wNum1 dw 4321 wNum2 dw 1234 wAns dw 0 dNum1 dd 42000 dNum2 dd 73000 dAns dd 0 qNum1 dq 42000000 qNum2 dq 73000000 qAns dq 0
To perform the basic operations of:
bAns = bNum1 + bNum2
wAns = wNum1 + wNum2
dAns = dNum1 + dNum2
qAns = qNum1 + qNum2
The following instructions could be used:
; bAns = bNum1 + bNum2
mov al, byte [bNum1]
add al, byte [bNum2]
mov byte [bAns], al
; wAns = wNum1 + wNum2
mov ax, word [wNum1]
add ax, word [wNum2]
mov word [wAns], ax
; dAns = dNum1 + dNum2
mov eax, dword [dNum1]
add eax, dword [dNum2]
mov dword [dAns], eax
; qAns = qNum1 + qNum2
mov rax, qword [qNum1]
add rax, qword [qNum2]
mov qword [qAns], rax
For some instructions, including those above, the explicit type specification (e.g., byte, word, dword, qword) can be omitted as the other operand will clearly define the size. It is included for consistency and good programming practice.
In addition to the basic add instruction, there is an increment instruction that will add one to the specified operand. The general form of the increment instruction is as follows:
inc <operand>
Where operation is as follows:
<operand> = <operand> + 1
The result is exactly the same as using the add instruction (and adding one). When using a memory operand, the explicit type specification (e.g., byte, word, dword, qword) is required to clearly define the size.
For example, assuming the following data declarations:
bNum db 42
wNum dw 4321
dNum dd 42000
qNum dq 42000000
To perform, the basic operations of:
rax = rax + 1
bNum = bNum + 1
wNum = wNum + 1
dNum = dNum + 1
qNum = qNum + 1
The following instructions could be used:
inc rax ; rax = rax + 1 inc byte [bNum] ; bNum = bNum + 1 inc word [wnum] ; wNum = wNum + 1 inc dword [dNum] ; dNum = dNum + 1 inc qword [qNum] ; qNum = qNum + 1
The addition instruction operates the same on signed and unsigned data. It is the programmer's responsibility to ensure that the data types and sizes are appropriate for the operations being performed.
The integer addition instructions are summarized as follows:
| Instruction | Explanation |
add <dest>, <src> |
Add two operands, (<dest> + <src>) and place the result in <dest> (over-writing previous value). Note 2, destination operand cannot be an immediate. |
| Examples: |
add cx, word [wVvar] add rax, 42 add dword [dVar], eax add qword [qVar], 300 |
inc <operand> |
Increment <operand> by 1. Note, <operand> cannot be an immediate. |
| Examples: |
inc word [wVvar] inc rax inc dword [dVar] inc qword [qVar] |
A more complete list of the instructions is located in Appendix B.
Addition with Carry
The add with carry is a special add instruction that will include a carry from a previous addition operation. This is useful when adding very large numbers, specifically numbers larger than the register size of the machine.
Using a carry in addition is fairly standard. For example, consider the following operation.
17
+ 25
----
42
As you may recall, the least significant digits (7 and 5) are added first. The result of 12 is noted as a 2 with a 1 carry. The most significant digits (1 and 2) are added along with the previous carry (1 in this example) resulting in a 4.
As such, two addition operations are required. Since there is no carry possible with the least significant portion, a regular addition instruction is used. The second addition operation would need to include a possible carry from the previous operation and must be done with an add with carry instruction. Additionally, the add with carry must immediately follow the initial addition operation to ensure that the rFlag register is not altered by an unrelated instruction (thus possibly altering the carry bit).
For assembly language programs the Least Significant Quadword (LSQ) is added with the add instruction and then immediately the Most Significant Quadword (MSQ) is added with the adc which will add the quadwords and include a carry from the previous addition operation.
The general form of the integer add with carry instruction is as follows:
adc <dest>, <src>
Where operation performs the following:
<dest> = <dest> + <src> + <carryBit>
Specifically, the source and destination operands along with the carry bit are added and the result is placed in the destination operand (over-writing the previous value). The carry bit is part of the rFlag register. The value of the source operand is unchanged. The destination and source operand must be of the same size (both bytes, both words, etc.). The destination operand cannot be an immediate. Both operands, cannot be memory. If a memory to memory addition operation is required, two instructions must be used.
For example, given the following declarations;
dquad1 ddq 0x1A000000000000000
dquad2 ddq 0x2C000000000000000
dqSum ddq 0
Each of the variables dquad1, dquad2, and dqSum are 128-bits and thus will exceed the machine 64-bit register size. However, two 64-bit registers can be used for each of the 128-bit values. This requires two move instructions, one for each 64-bit register. For example,
mov rax, qword [dquad1]
mov rdx, qword [dquad1+8]
The first move to the rax register accesses the first 64-bits of the 128-bit variable. The second move to the rdx register access the next 64-bits of the 128-bit variable. This is accomplished by using the variable starting address, dquad1 and adding 8 bytes, thus skipping the first 64-bits (or 8 bytes) and accessing the next 64-bits.
If the LSQ's are added and then the MSQ's are added including any carry, the 128-bit result can be correctly obtained. For example,
mov rax, qword [dquad1]
mov rdx, qword [dquad1+8]
add rax, qword [dquad2]
adc rdx, qword [dquad2+8]
mov qword [dqSum],
rax mov qword [dqSum+8], rdx
Initially, the LSQ of dquad1 is placed in rax and the MSQ is placed in rdx. Then the add instruction will add the 64-bit rax with the LSQ of dquad2 and, in this example, provide a carry of 1 with the result in rax. Then the rdx is added with the MSQ of dquad2 along with the carry via the adc instruction and the result placed in rdx.
The integer add with carry instruction is summarized as follows:
| Instruction | Explanation |
adc <dest>, <src> |
Add two operands, (<dest> + <src>) and any previous carry (stored in the carry bit in the rFlag register) and place the result in <dest> (over-writing previous value). Note 1, both operands cannot be memory. Note 2, destination operand cannot be an immediate. |
| Examples: |
adc rcx, qword [dVvar1] adc rax, 42 |
A more complete list of the instructions is located in Appendix B.
Subtraction
The general form of the integer subtraction instruction is as follows:
sub <dest>, <src>
Where operation performs the following:
<dest> = <dest> - <src>
Specifically, the source operand is subtracted from the destination operand and the result is placed in the destination operand (over-writing the previous value). The value of the source operand is unchanged. The destination and source operand must be of the same size (both bytes, both words, etc.). The destination operand cannot be an immediate. Both operands, cannot be memory. If a memory to memory subtraction operation is required, two instructions must be used.
For example, assuming the following data declarations:
bNum1 db 73 bNum2 db 42 bAns db 0 wNum1 dw 1234 wNum2 dw 4321 wAns dw 0 dNum1 dd 73000 dNum2 dd 42000 dAns dd 0 qNum1 dq 73000000 qNum2 dq 73000000 qAns dd 0
To perform, the basic operations of:
bAns = bNum1 - bNum2
wAns = wNum1 - wNum2
dAns = dNum1 - dNum2
qAns = qNum1 - qNum2
The following instructions could be used:
; bAns = bNum1 - bNum2
mov al, byte [bNum1]
sub al, byte [bNum2]
mov byte [bAns], al
; wAns = wNum1 – wNum2
mov ax, word [wNum1]
sub ax, word [wNum2]
mov word [wAns], ax
; dAns = dNum1 – dNum2
mov eax, dword [dNum1]
sub eax, dword [dNum2]
mov dword [dAns], eax
; qAns = qNum1 - qNum2
mov rax, qword [qNum1]
sub rax, qword [qNum2]
mov qword [qAns], rax
For some instructions, including those above, the explicit type specification (e.g., byte, word, dword, qword) can be omitted as the other operand will clearly define the size. It is included for consistency and good programming practices.
In addition to the basic subtract instruction, there is a decrement instruction that will subtract one from the specified operand. The general form of the decrement instruction is as follows:
dec <operand>
Where operation performs the following:
<operand> = <operand> - 1
The result is exactly the same as using the subtract instruction (and subtracting one). When using a memory operand, the explicit type specification (e.g., byte, word, dword, qword) is required to clearly define the size.
For example, assuming the following data declarations:
bNum db 42
wNum dw 4321
dNum dd 42000
qNum dq 42000000
To perform, the basic operations of:
rax = rax - 1
bNum = bNum - 1
wNum = wNum - 1
dNum = dNum - 1
qNum = qNum - 1
The following instructions could be used:
dec rax ; rax = rax - 1 dec byte [bNum] ; bNum = bNum - 1 dec word [wNum] ; wNum = wNum - 1 dec dword [dNum] ; dNum = dNum - 1 dec qword [qNum] ; qNum = qNum - 1
The subtraction instructions operate the same on signed and unsigned data. It is the programmer's responsibility to ensure that the data types and sizes are appropriate for the operations being performed.
The integer subtraction instructions are summarized as follows:
| Instruction | Explanation |
sub <dest>, <src> |
Subtract two operands, (<dest> - <src>) and place the result in <dest> (over-writing previous value). Note 1, both operands cannot be memory. Note 2, destination operand cannot be an immediate. |
| Examples: |
sub cx, word [wVvar] sub rax, 42 sub dword [dVar], eax sub qword [qVar], 300 |
dec <operand> |
Decrement <operand> by 1. Note, <operand> cannot be an immediate. |
| Examples: |
dec word [wVvar] dec rax dec dword [dVar] dec qword [qVar] |
A more complete list of the instructions is located in Appendix B.
Integer Multiplication
The multiply instruction multiplies two integer operands. Mathematically, there are special rules for handling multiplication of signed values. As such, different instructions are used for unsigned multiplication (mul) and signed multiplication (imul).
Multiplication typically produces double sized results. That is, multiplying two n-bit values produces a 2n-bit result. Multiplying two 8-bit numbers will produce a 16-bit result. Similarly, multiplication of two 16-bit numbers will produce a 32-bit result, multiplication of two 32-bit numbers will produce a 64-bit result, and multiplication of two 64-bit numbers will produce a 128-bit result.
There are many variants for the multiply instruction. For the signed multiply, some forms will truncate the result to the size of the original operands. It is the programmer's responsibility to ensure that the values used will work for the specific instructions selected.
Unsigned Multiplication
The general form of the unsigned multiplication is as follows:
mu1 <src>
Where the source operand must be a register or memory location. An immediate operand is not allowed.
For the single operand multiply instruction, the A register (al/ax/eax/rax) must be used for one of the operands (al for 8-bits, ax for 16-bits, eax for 32-bits, and rax for 64-bit). The other operand can be a memory location or register, but not an immediate. Additionally, the result will be placed in the A and possibly D registers, based on the sizes being multiplied. The following table shows the various options for the byte, word, double-word, and quadword unsigned multiplications.
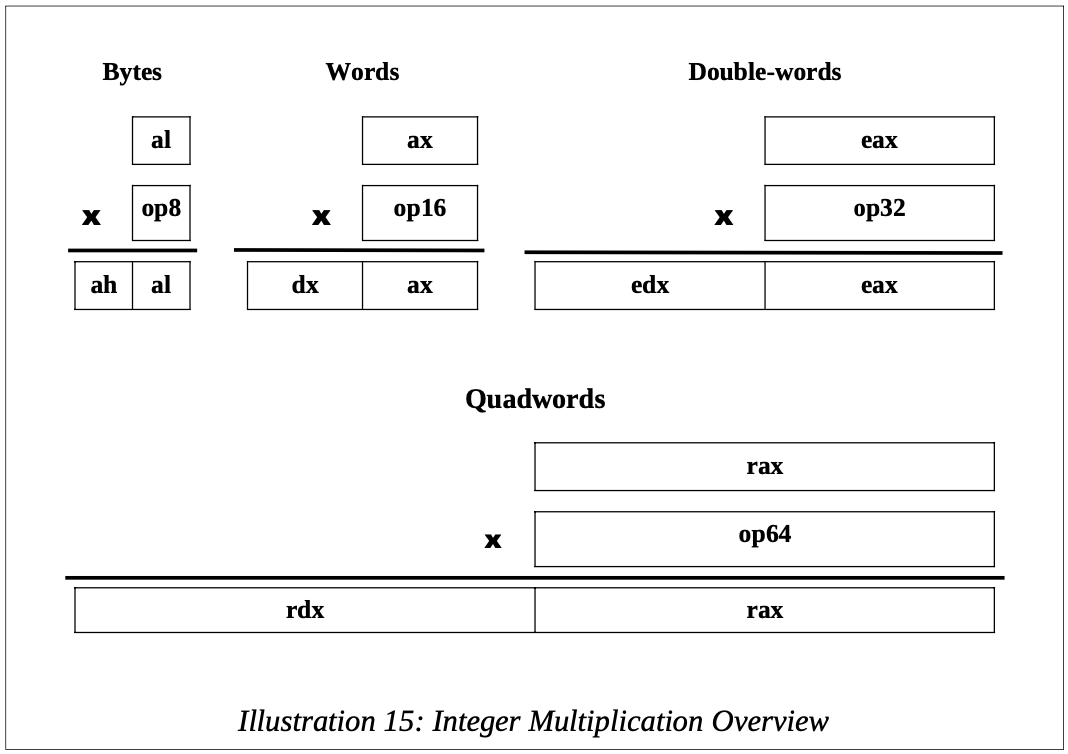
As shown in the chart, for most cases the integer multiply uses a combination of the A and D registers. This can be very confusing.
For example, when multiplying a rax (64-bits) times a quadword operand (64-bits), the multiplication instruction provides a double quadword result (128-bit). This can be useful and important when dealing with very large numbers. Since the 64-bit architecture only has 64-bit registers, the 128-bit result is, and must be, placed in two different quadword (64-bit) registers, rdx for the upper-order result and rax for the lower-order result, which is typically written as rdx:rax (by convention).
However, this use of two registers is applied to smaller sizes as well. For example, the result of multiplying ax (16-bits) times a word operand (also 16-bits) provides a double- word (32-bit) result. However, the result is not placed in eax (which might be easier), it is placed in two registers, dx for the upper-order result (16-bits) and ax for the lower- order result (16-bits), typically written as dx:ax (by convention). Since the double-word (32-bit) result is in two different registers, two moves may be required to save the result.
This pairing of registers, even when not required, is due to legacy support for previous earlier versions of the architecture. While this helps ensure backwards compatibility, it can be quite confusing.
For example, assuming the following data declarations:
bNumA db 42 bNumB db 73 wAns dw 0 wAns1 dw 0 wNumA dw 4321 wNumB dw 1234 dAns2 dd 0 dNumA dd 42000 dNumB dd 73000 qAns3 dq 0 qNumA dq 420000 qNumB dq 730000 dqAns4 ddq 0
To perform, the basic operations of:
wAns = bNumA^2 ; bNumA squared
bAns1 = bNumA * bNumB
wAns1 = bNumA * bNumB
wAns2 = wNumA * wNumB
dAns2 = wNumA * wNumB
dAns3 = dNumA * dNumB
qAns3 = dNumA * dNumB
qAns4 = qNumA * qNumB
dqAns4 = qNumA * qNumB
The following instructions could be used:
; wAns = bNumA^2 or bNumA squared
mov al, byte [bNumA]
mul al ; result in ax
mov word [wAns], ax
; wAns1 = bNumA * bNumB
mov al, byte [bNumA]
mul byte [bNumB] ; result in ax
mov word [wAns1], ax
; dAns2 = wNumA * wNumB
mov ax, word [wNumA]
mul word [wNumB] ; result in dx:ax
mov word [dAns2], ax
mov word [dAns2+2], dx
; qAns3 = dNumA * dNumB
mov eax, dword [dNumA]
mul dword [dNumB] ; result in edx:eax
mov dword [qAns3], eax
mov dword [qAns3+4], edx
; dqAns4 = qNumA * qNumB
mov rax, qword [qNumA]
mul qword [qNumB] ; result in rdx:rax
mov qword [dqAns4], rax
mov qword [dqAns4+8], rdx
For some instructions, including those above, the explicit type specification (e.g., byte, word, dword, qword) is required to clearly define the size.
The integer unsigned multiplication instruction is summarized as follows:
| Instruction | Explanation |
mu1 <src> mu1 <op8> mu1 <op16> mu1 <op32> mu1 <op64> |
Multiply A register (al, ax, eax, or rax) times the <src> operand. |
| Examples: |
mu1 word [wVvar] mu1 a1 mu1 dword [dVar] mu1 qword [qVar] |
A more complete list of the instructions is located in Appendix B.
Signed Multiplication
The signed multiplication allows a wider range of operands and operand sizes. The general forms of the signed multiplication are as follows:
imul <source>
imul <dest>, <src/imm>
imul <dest>, <src>, <imm>
In all cases, the destination operand must be a register. For the multiple operand multiply instruction, byte operands are not supported.
When using a single operand multiply instruction, the imul is the same layout as the mul (as previously presented). However, the operands are interpreted only as signed.
When two operands are used, the destination operand and the source operand are multiplied and the result placed in the destination operand (over-writing the previous value).
Specifically, the action performed is:
<dest> = <dest> * <src/imm>
For two operands, the <src/imm> operand may be a register, memory location, or immediate value. The size of the immediate value is limited to the size of the source operand, up to a double-word size (32-bit), even for quadword (64-bit) multiplications. The final result is truncated to the size of the destination operand. A byte sized destination operand is not supported.
When three operands are used, two operands are multiplied and the result placed in the destination operand. Specifically, the action performed is:
<dest> = <src> * <imm>
For three operands, the <src> operand must be a register or memory location, but not an immediate. The <imm> operand must be an immediate value. The size of the immediate value is limited to the size of the source operand, up to a double-word size (32-bit), even for quadword multiplications. The final result is truncated to the size of the destination operand. A byte sized destination operand is not supported.
It should be noted that when the multiply instruction provides a larger type, the original type may be used. For this to work, the values multiplied must fit into the smaller size which limits the range of the data. For example, when two double-words are multiplied and a quadword result is provided, the least significant double-word (of the quadword)
will contain the answer if the values are sufficiently small which is often the case. This is typically done in high-level languages when an int (32-bit integer) variable is multiplied by another int variable and assigned to an int variable.
For example, assuming the following data declarations:
wNumA dw 1200 wNumB dw -2000 wAns1 dw 0 wAns2 dw 0 dNumA dd 42000 dNumB dd -13000 dAns1 dd 0 dAns2 dd 0 qNumA dq 120000 qNumB dq -230000 qAns1 dq 0 qAns2 dq 0
To perform, the basic operations of:
wAns1 = wNumA * -13
wAns2 = wNumA * wNumB
dAns1 = dNumA * 113
dAns2 = dNumA * dNumB
qAns1 = qNumA * 7096
qAns2 = qNumA * qNumB
The following instructions could be used:
; wAns1 = wNumA * -13
mov ax, word [wNumA]
imul ax, -13 ; result in ax
mov word [wAns1], ax
; wAns2 = wNumA * wNumB
mov ax, word [wNumA]
imul ax, word [wNumB] ; result in ax
mov word [wAns2], ax
; dAns1 = dNumA * 113
mov eax, dword [dNumA]
imul eax, 113 ; result in ax
mov dword [dAns1], eax
; dAns2 = dNumA * dNumB
mov eax, dword [dNumA]
imul eax, dword [dNumB] ; result in ax
mov dword [dAns2], eax
; qAns1 = qNumA * 7096
mov rax, qword [qNumA]
imul rax, 7096 ; result in ax
mov qword [qAns1], rax
; qAns2 = qNumA * qNumB
mov rax, qword [qNumA]
imul rax, qword [qNumB] ; result in ax
mov qword [qAns2], rax
Another way to perform the multiplication of
qAns1 = qNumA * 7096
Would be as follows:
; qAns1 = qNumA * 7096
mov rcx, qword [qNumA]
imul rbx, rcx, 7096 ; result in ax
mov qword [qAns1], rbx
This example shows the three-operand multiply instruction using different registers.
In these examples, the multiplication result is truncated to the size of the destination operand. For a full-sized result, the single operand instruction should be used (as fully described in the section regarding unsigned multiplication).
For some instructions, including those above, the explicit type specification (e.g., byte, word, dword, qword) may not be required to clearly define the size.
The integer signed multiplication instruction is summarized as follows:
| Instruction | Explanation |
imu1 <src> imu1 <dest>, <src/imm32> imu1 <dest>, <src>, <imm32> imu1 <op8> imu1 <op16> imu1 <op32> imu1 <op64> imu1 <reg16>, <op16/imm> imu1 <reg32>, <op32/imm> imu1 <reg64>, <op64/imm> imu1 <reg16>, <op16>, <imm> imu1 <reg32>, <op32>, <imm> imu1 <reg64>, <op64>, <imm> |
Signed multiply instruction. For single operand: Note, <src> operand cannot be an immediate. For two operands: For three operands: |
| Examples: |
imu1 ax, 17 imu1 a1 imu1 abx, dword [dVar] imu1 rbx, dword [dVar], 791 imu1 rcx, qword [qVar] imu1 qword [qVar] |
A more complete list of the instructions is located in Appendix B.
Integer Division
The division instruction divides two integer operands. Mathematically, there are special rules for handling division of signed values. As such, different instructions are used for unsigned division (div) and signed division (idiv).
Recall that \(\dfrac{dividend}{divisor} = quotient\)
Division requires that the dividend must be a larger size than the divisor. In order to divide by an 8-bit divisor, the dividend must be 16-bits (i.e., the larger size). Similarly, a 16-bit divisor requires a 32-bit dividend. And, a 32-bit divisor requires a 64-bit dividend.
Like the multiplication, for most cases the integer division uses a combination of the A and D registers. This pairing of registers is due to legacy support for previous earlier versions of the architecture. While this helps ensure backwards compatibility, it can be quite confusing.
Further, the A, and possibly the D register, must be used in combination for the dividend.
- Byte Divide: ax for 16-bits
- Word Divide: dx:ax for 32-bits
- Double-word divide: edx:eax for 64-bits
- Quadword Divide: rdx:rax for 128-bits
Setting the dividend (top operand) correctly is a key source of problems. For the word, double-word, and quadword division operations, the dividend requires both the D register (for the upper-order portion) and A (for the lower-order portion).
Setting these correctly depends on the data type. If a previous multiplication was performed, the D and A registers may already be set correctly. Otherwise, a data item may need to be converted from its current size to a larger size with the upper-order portion being placed in the D register. For unsigned data, the upper portion will always be zero. For signed data, the existing data must be sign extended as noted in a previous section, Signed Conversions.
The divisor can be a memory location or register, but not an immediate. Additionally, the result will be placed in the A register (al/ax/eax/rax) and the remainder in either the ah, dx, edx, or rdx register. Refer to the Integer Division Overview table to see the layout more clearly.
The use of a larger size operand for the dividend matches the single operand multiplication. For simple divisions, an appropriate conversion may be required in order to ensure the dividend is set correctly. For unsigned divisions, the upper-order part of the dividend can set to zero. For signed divisions, the upper-order part of the dividend can be set with an applicable conversion instruction.
As always, division by zero will crash the program and damage the space-time continuum. So, try not to divide by zero.
The following tables provide an overview of the divide instruction for bytes, words, double-words, and quadwords.
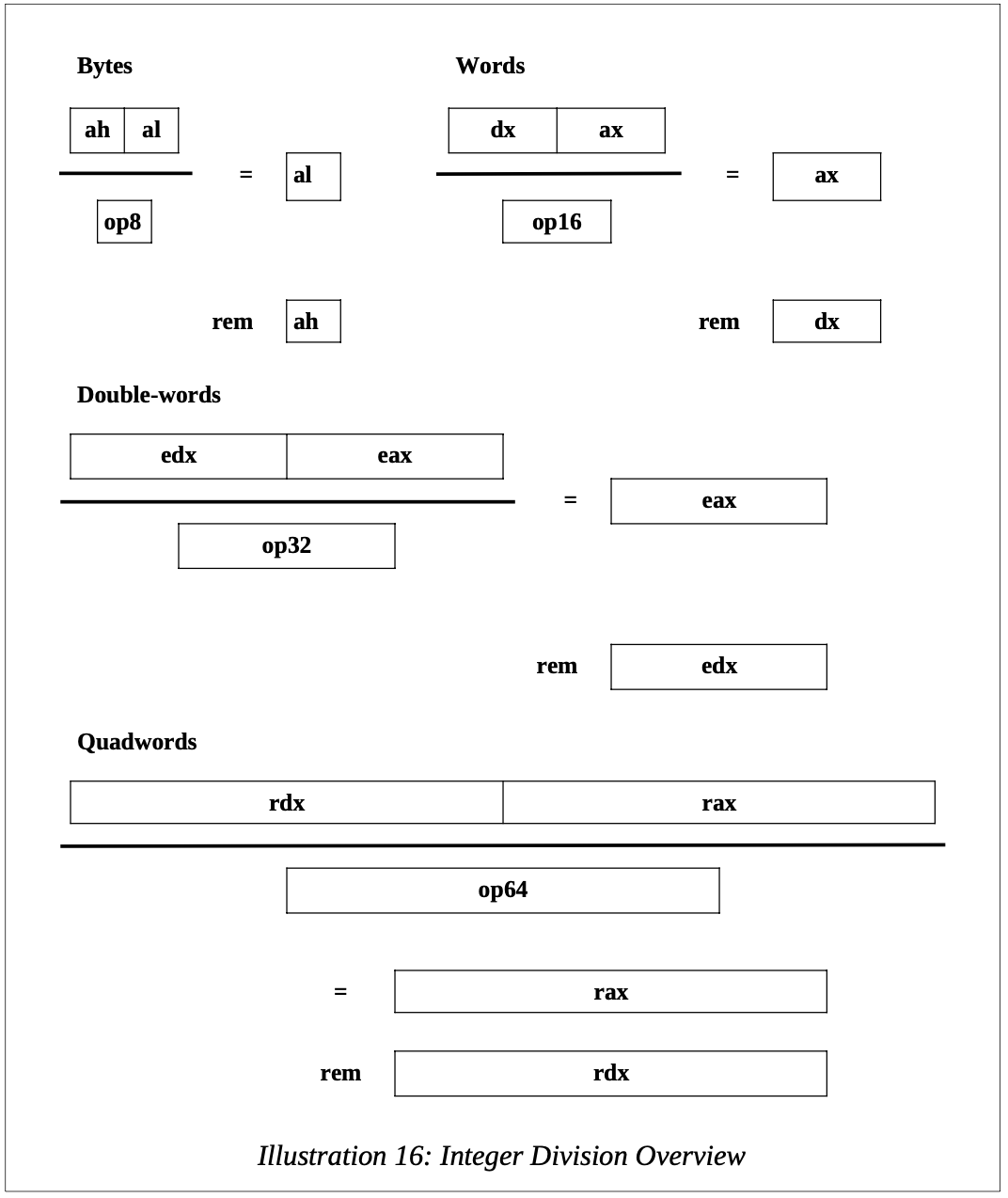
The signed and unsigned division instructions operate in the same manner. However, the range values that can be divided is different. The programmer is responsible for ensuring that the values being divided are appropriate for the operand sizes being used.
The general forms of the unsigned and signed division are as follows:
div <src> ; unsigned division
idiv <src> ; signed division
The source operand and destination operands (A and D registers) are described in the preceding table.
For example, assuming the following data declarations:
bNumA db 63
bNumB db 17
bNumC db 5
bAns1 db 0
bAns2 db 0
bRem2 db 0
bAns3 db 0
wNumA dw 4321
wNumB dw 1234
wNumC dw 167
wAns1 dw 0
wAns2 dw 0
wRem2 dw 0
wAns3 dw 0
dNumA dd 42000
dNumB dd -3157
dNumC dd -293
dAns1 dd 0
dAns2 dd 0
dRem2 dd 0
dAns3 dd 0
qNumA dq 730000
qNumB dq -13456
qNumC dq -1279
qAns1 dq 0
qAns2 dq 0
qRem2 dq 0
qAns3 dq 0
To perform, the basic operations of:
bAns1 = bNumA / 3 ; unsigned
bAns2 = bNumA / bNumB ; unsigned
bRem2 = bNumA % bNumB ; % is modulus
bAns3 = (bNumA * bNumC) / bNumB ; unsigned
wAns1 = wNumA / 5 ; unsigned
wAns2 = wNumA / wNumB ; unsigned
wRem2 = wNumA % wNumB ; % is modulus
wAns3 = (wNumA * wNumC) / wNumB ; unsigned
dAns = dNumA / 7 ; unsigned
dAns3 = dNumA * dNumB ; unsigned
dRem1 = dNumA % dNumB ; % is modulus
dAns3 = (dNumA * dNumC) / dNumB ; unsigned
qAns = qNumA / 9 ; unsigned
qAns4 = qNumA * qNumB ; unsigned
qRem1 = qNumA % qNumB ; % is modulus
qAns3 = (qNumA * qNumC) / qNumB ; unsigned
The following instructions could be used:
; -----
; example byte operations, unsigned
; bAns1 = bNumA / 3 (unsigned) mov al, byte [bNumA]
mov ah, 0
mov bl, 3
div bl ; a1 = ax / 3
mov byte [bAns1], al
; bAns2 = bNumA / bNumB (unsigned)
mov ax, 0
mov al, byte [bNumA]
div byte [bNumB] ; a1 = ax / bNumB
mov byte [bAns2], al
mov byte [bRem2], ah ; ah = ax % bNumB
; bAns3 = (bNumA * bNumC) / bNumB (unsigned)
mov al, byte [bNumA]
mul byte [bNumC] ; result in ax
div byte [bNumB] ; a1 = ax / bNumB
mov byte [bAns3], al
; -----
; example word operations, unsigned
; wAns1 = wNumA / 5 (unsigned)
mov ax, word [wNumA]
mov dx, 0
mov bx, 5
div bx ; ax = dx:ax/5
mov word [wAns1], ax
; wAns2 = wNumA / wNumB (unsigned)
mov dx, 0
mov ax, word [wNumA]
div word [wNumB] ; ax = dx:ax / wNumB
mov word [wAns2], ax
mov word [wRem2], dx
; wAns3 = (wNumA * wNumC) / wNumB (unsigned)
mov ax, word [wNumA]
mul word [wNumC] ; ; result in dx:ax
div word [wNumB] ; ; ax = dx:ax / wNumB
mov word [wAns3], ax
; -----
; example double-word operations, signed
; dAns1 = dNumA / 7 (signed)
mov eax, dword [dNumA]
cdq ; eax → edx:eax
mov ebx, 7
idiv ebx ; eax = edx:eax / 7
mov dword [dAns1], eax
; dAns2 = dNumA / dNumB (signed)
mov eax, dword [dNumA]
cdq ; eax → edx:eax
idiv dword [dNumB] ; eax = edx:eax/dNumB
mov dword [dAns2], eax
mov dword [dRem2], edx ; edx = edx:eax%dNumB
; dAns3 = (dNumA * dNumC) / dNumB (signed)
mov eax, dword [dNumA]
imul dword [dNumC] ; result in edx:eax
idiv dword [dNumB] ; eax = edx:eax/dNumB
mov dword [dAns3], eax
; -----
; example quadword operations, signed
; qAns1 = qNumA / 9 (signed)
mov rax, qword [qNumA]
cqo ; rax → rdx:rax
mov rbx, 9
idiv rbx ; eax = edx:eax / 9
mov qword [qAns1], rax
; qAns2 = qNumA / qNumB (signed)
mov rax, qword [qNumA]
cqo ; rax → rdx:rax
idiv qword [qNumB] ; rax = rdx:rax/qNumB
mov qword [qAns2], rax
mov qword [qRem2], rdx ; rdx = rdx:rax%qNumB
; qAns3 = (qNumA * qNumC) / qNumB (signed)
mov rax, qword [qNumA]
imul qword [qNumC] ; result in rdx:rax
idiv qword [qNumB] ; rax = rdx:rax/qNumB
mov qword [qAns3], rax
For some instructions, including those above, the explicit type specification (e.g., byte, word, dword, qword) is required to clearly define the size.
The integer division instructions are summarized as follows:
| Instruction | Explanation |
div <src> div <op8> div <op16> div <op32> div <op64> |
Unsigned divide A/D register (ax, dx:ax, edx:eax, or rdx:rax) by the <src> operand. Byte: al = ax / <src>, rem in ah Word: ax = dx:ax / <src>, rem in dx Double: eax = eax / <src>, rem in edx Quad: rax = rax / <src>, rem in rdx Note, <src> operand cannot be an immediate. |
| Examples: |
div word [wVvar] div bl div dword [dVar] div qword [qVar] |
idiv <src> idiv <op8> idiv <op16> idiv <op32> idiv <op64> |
Signed divide A/D register (ax, dx:ax, edx:eax, or rdx:rax) by the <src> operand. Byte: al = ax / <src>, rem in ah Word: ax = dx:ax / <src>, rem in dx Double: eax = eax / <src>, rem in edx Quad: rax = rax / <src>, rem in rdx Note, <src> operand cannot be an immediate. |
| Examples: |
idiv word [wVvar] idiv bl idiv dword [dVar] idiv qword [qVar] |
A more complete list of the instructions is located in Appendix B.


