Skip to main content
Engineering LibreTexts

7.6: Logical Instructions

  1. Last updated
  2. Save as PDF
  • Page ID
    19902

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    This section summarizes some of the more common logical instructions that may be useful when programming.

    Logical Operations

    As you should recall, below are the truth tables for the basic logical operations;

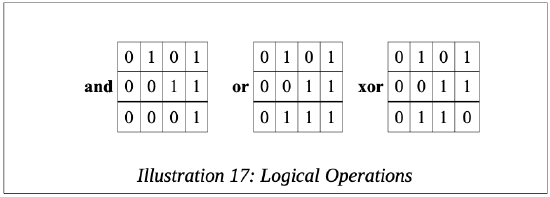
    截屏2021-07-23 上午10.29.25.png

    The logical instructions are summarized as follows:

    Instruction

    Explanation 

    and   <dest>, <src>

    Perform logical AND operation on two operands, (<dest> and <src>) and place the result in <dest> (over-writing previous value).
    Note 1, both operands cannot be memory.
    Note 2, destination operand cannot be an immediate.

    Examples:

    		 
    and   ax, bx
and   rcx, rdx
and   eax, dword [dNum]
and   qword [qNum], rdx

    or   <dest>, <src>

    Perform logical OR operation on two operands, (<dest> || <src>) and place the result in <dest> (over-writing previous value).
    Note 1, both operands cannot be memory.
    Note 2, destination operand cannot be an immediate.

    Examples:

    		 
    or   ax, bx
or   rcx, rdx
or   eax, dword [dNum]
or   qword [qNum], rdx

    xor   <dest>, <src>

    Perform logical XOR operation on two operands, (<dest> ^ <src>) and place the result in <dest> (over-writing previous value).
    Note 1, both operands cannot be memory.
    Note 2, destination operand cannot be an immediate.

    Examples:

    		 
    xor   ax, bx
xor   rcx, rdx
xor   eax, dword [dNum]
xor   qword [qNum], rdx

    not   <op>

    Perform a logical not operation (one's complement on the operand 1's→0's and 0's→1's).
    Note, operand cannot be an immediate.

    Examples:

    		 
    not   bx
not   rdx
not   dword [dNum]
not   qword [qNum]

    The & refers to the logical AND operation, the || refers to the logical OR operation, and the ^ refers to the logical XOR operation as per C/C++ conventions. The ¬ refers to the logical NOT operation.

    A more complete list of the instructions is located in Appendix B.

    Shift Operations

    The shift operation shifts bits within an operand, either left or right. Two typical reasons for shifting bits include isolating a subset of the bits within an operand for some specific purpose or possibly for performing multiplication or division by powers of two. All bits are shifted one position. The bit that is shifted outside the operand is lost and a 0-bit added at the other side.

    Logical Shift

    The logical shift is a bitwise operation that shifts all the bits of its source register by the specified number of bits and places the result into the destination register. The bits can be shifted left or right as needed. Every bit in the source operand is moved the specified number of bit positions and the newly vacant bit positions are filled in with zeros.

    The following diagram shows how the right and left shift operations work for byte sized operands.

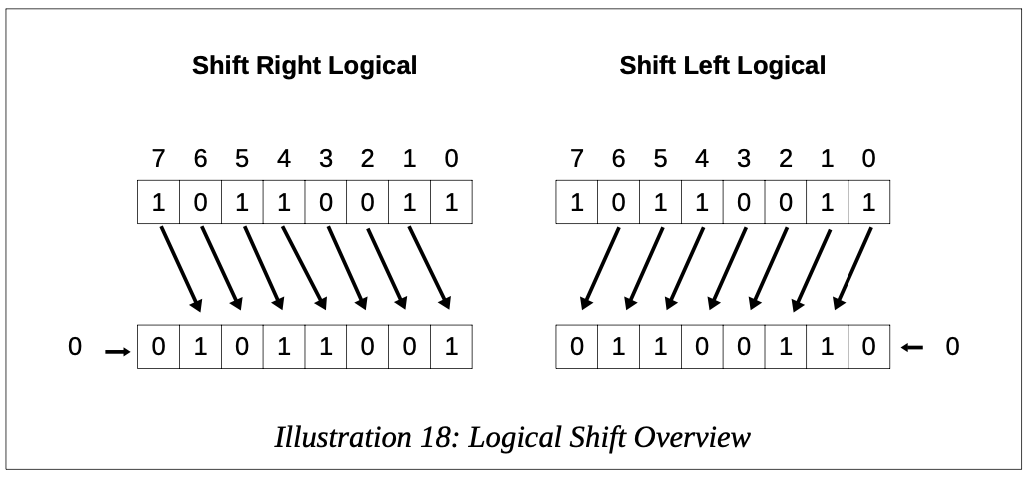
    截屏2021-07-23 上午10.42.09.png

    The logical shift treats the operand as a sequence of bits rather than as a number.

    The shift instructions may be used to perform unsigned integer multiplication and division operations for powers of 2. Powers of two would be 2, 4, 8, etc. up to the limit of the operand size (32-bits for register operands).

    In the examples below, 23 is divided by 2 by performing a shift right logical one bit. The resulting 11 is shown in binary. Next, 13 is multiplied by 4 by performing a shift left logical two bits. The resulting 52 is shown in binary.

    截屏2021-07-23 上午10.42.33.png

    As can be seen in the examples, a 0 was entered in the newly vacated bit locations on either the right or left (depending on the operation).

    The logical shift instructions are summarized as follows:

    Instruction

    Explanation 

    shl   <dest>, <imm>
shl   <dest>, cl

    Perform logical shift left operation on destination operand. Zero fills from right (as needed).
    The <imm> or the value in cl register must be between 1 and 64.
    Note, destination operand cannot be an immediate.

    Examples:

    		 
    shl   ax, 8
shl   rcx, 32
shl   eax, cl
shl   qword [qNum], cl

    shr   <dest>, <imm>
shr   <dest>, cl

    Perform logical shift right operation on destination operand. Zero fills from left (as needed).
    The <imm> or the value in cl register must be between 1 and 64.
    Note, destination operand cannot be an immediate.

    Examples:

    		 
    shr   ax, 8
shr   rcx, 32
shr   eax, cl
shr   qword [qNum], cl

    A more complete list of the instructions is located in Appendix B.

    7.6.2.2 Arithmetic Shift

    The arithmetic shift right is also a bitwise operation that shifts all the bits of its source register by the specified number of bits and places the result into the destination register. Every bit in the source operand is moved the specified number of bit positions, and the newly vacant bit positions are filled in. For an arithmetic left shift, the original leftmost bit (the sign bit) is replicated to fill in all the vacant positions. This is referred to as sign extension.

    The following diagrams show how the shift left and shift right arithmetic operations works for a byte sized operand.

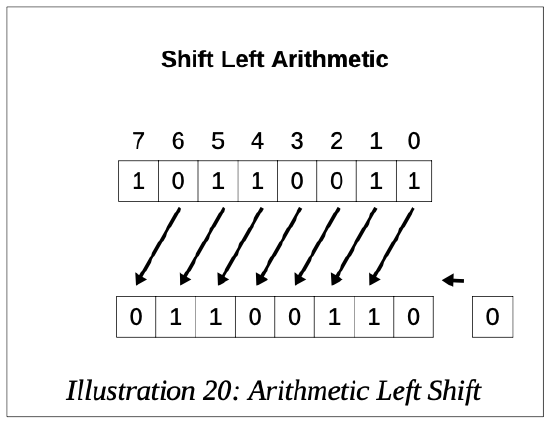
    截屏2021-07-23 上午10.44.10.png

    The arithmetic left shift moves bits the number of specified places to the left and zero fills the from the least significant bit position (left). The leading sign bit is not preserved. The arithmetic left shift can be useful to perform an efficient multiplication by a power of two. If the resulting value does not fit an overflow is generated.

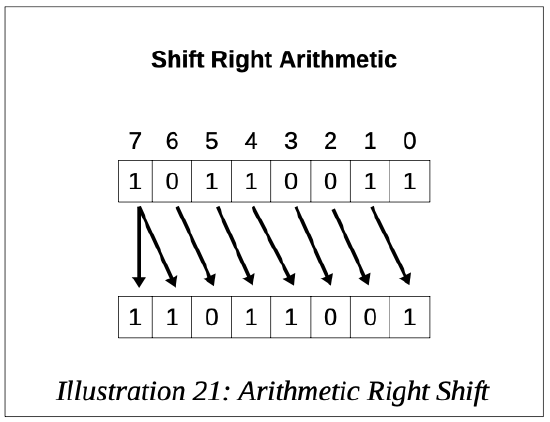
    截屏2021-07-23 上午10.48.28.png

    The arithmetic right shift moves bits the number of specified places to the right and treats the operand as a signed number which extends the sign (negative in this example).

    The arithmetic shift rounds always rounds down (towards negative infinity) and the standard divide instruction truncates (rounds toward 0). As such, the arithmetic shift is not typically used to replace the signed divide instruction.

    The arithmetic shift instructions are summarized as follows:

    Instruction

    Explanation 

    sal   <dest>, <imm>
sal   <dest>, cl

    Perform arithmetic shift left operation on destination operand. Zero fills from right (as needed).
    The <imm> or the value in cl register must be between 1 and 64.

    Note, destination operand cannot be an immediate.

    Examples:

    		 
    sal   ax, 8
sal   rcx, 32
sal   eax, cl
sal   qword [qNum], cl

    sar   <dest>, <imm>
sar   <dest>, cl

    Perform arithmetic shift right operation on destination operand. Sign fills from left (as needed).
    The <imm> or the value in cl register must be between 1 and 64.

    Note, destination operand cannot be an immediate.

    Examples:

    		 
    sar   ax, 8
sar   rcx, 32
sar   eax, cl
sar   qword [qNum], cl

    A more complete list of the instructions is located in Appendix B.

    7.6.3 Rotate Operations

    The rotate operation shifts bits within an operand, either left or right, with the bit that is shifted outside the operand is rotated around and placed at the other end.

    For example, if a byte operand, \(10010110_2\), is rotated to the right 1 place, the result would be \(01001011_2\). If a byte operand, \(10010110_2\), is rotated to the left 1 place, the result would be \(00101101_2\).

    The logical shift instructions are summarized as follows:

    Instruction

    Explanation 

    rol   <dest>, <imm>
rol   <dest>, cl

    Perform rotate left operation on destination operand.
    The <imm> or the value in cl register must be between 1 and 64.

    Note, destination operand cannot be an immediate.

    Examples:

    		 
    rol   ax, 8
rol   rcx, 32
rol   eax, cl
rol   qword [qNum], cl

    ror   <dest>, <imm>
ror   <dest>, cl

    Perform rotate right operation on destination operand.
    The <imm> or the value in cl register must be between 1 and 64.

    Note, destination operand cannot be an immediate.

    Examples:

    		 
    ror   ax, 8
ror   rcx, 32
ror   eax, cl
ror   qword [qNum], cl

    A more complete list of the instructions is located in Appendix B.

    This page titled 7.6: Logical Instructions is shared under a CC BY-NC-SA license and was authored, remixed, and/or curated by Ed Jorgensen.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Author
      Ed Jorgensen
      Autonumber Section Headings
      title with colon delimiters
      License
      CC BY-NC-SA
      Show TOC
      no
    2. Tags
      This page has no tags.