3.4: Small to big systems
- Page ID
- 77126
As Moore's law has predicted, computing power has been growing at a furious pace and shows no signs of slowing down. It is relatively uncommon for any high end servers to contain only a single CPU. This is achieved in a number of different fashions.
Symmetric Multi-Processing, commonly shortened to SMP, is currently the most common configuration for including multiple CPUs in a single system.
The symmetric term refers to the fact that all the CPUs in the system are the same (e.g. architecture, clock speed). In a SMP system there are multiple processors that share other all other system resources (memory, disk, etc).
For the most part, the CPUs in the system work independently; each has its own set of registers, program counter, etc. Despite running separately, there is one component that requires strict synchronisation.
This is the CPU cache; remember the cache is a small area of quickly accessible memory that mirrors values stored in main system memory. If one CPU modifies data in main memory and another CPU has an old copy of that memory in its cache the system will obviously not be in a consistent state. Note that the problem only occurs when processors are writing to memory, since if a value is only read the data will be consistent.
To co-ordinate keeping the cache coherent on all processors an SMP system uses snooping. Snooping is where a processor listens on a bus which all processors are connected to for cache events, and updates its cache accordingly.
One protocol for doing this is the MOESI protocol; standing for Modified, Owner, Exclusive, Shared, Invalid. Each of these is a state that a cache line can be in on a processor in the system. There are other protocols for doing as much, however they all share similar concepts. Below we examine MOESI so you have an idea of what the process entails.
When a processor requires reading a cache line from main memory, it firstly has to snoop all other processors in the system to see if they currently know anything about that area of memory (e.g. have it cached). If it does not exist in any other process, then the processor can load the memory into cache and mark it as exclusive. When it writes to the cache, it then changes state to be modified. Here the specific details of the cache come into play; some caches will immediately write back the modified cache to system memory (known as a write-through cache, because writes go through to main memory). Others will not, and leave the modified value only in the cache until it is evicted, when the cache becomes full for example.
The other case is where the processor snoops and finds that the value is in another processors cache. If this value has already been marked as modified, it will copy the data into its own cache and mark it as shared. It will send a message for the other processor (that we got the data from) to mark its cache line as owner. Now imagine that a third processor in the system wants to use that memory too. It will snoop and find both a shared and a owner copy; it will thus take its value from the owner value. While all the other processors are only reading the value, the cache line stays shared in the system. However, when one processor needs to update the value it sends an invalidate message through the system. Any processors with that cache line must then mark it as invalid, because it not longer reflects the "true" value. When the processor sends the invalidate message, it marks the cache line as modified in its cache and all others will mark as invalid (note that if the cache line is exclusive the processor knows that no other processor is depending on it so can avoid sending an invalidate message).
From this point the process starts all over. Thus whichever processor has the modified value has the responsibility of writing the true value back to RAM when it is evicted from the cache. By thinking through the protocol you can see that this ensures consistency of cache lines between processors.
There are several issues with this system as the number of processors starts to increase. With only a few processors, the overhead of checking if another processor has the cache line (a read snoop) or invalidating the data in every other processor (invalidate snoop) is manageable; but as the number of processors increase so does the bus traffic. This is why SMP systems usually only scale up to around 8 processors.
Having the processors all on the same bus starts to present physical problems as well. Physical properties of wires only allow them to be laid out at certain distances from each other and to only have certain lengths. With processors that run at many gigahertz the speed of light starts to become a real consideration in how long it takes messages to move around a system.
Note that system software usually has no part in this process, although programmers should be aware of what the hardware is doing underneath in response to the programs they design to maximise performance.
In the section called “Cache in depth” we described inclusive v exclusive caches. In general, L1 caches are usually inclusive — that is all data in the L1 cache also resides in the L2 cache. In a multiprocessor system, an inclusive L1 cache means that only the L2 cache need snoop memory traffic to maintain coherency, since any changes in L2 will be guaranteed to be reflected by L1. This reduces the complexity of the L1 and de-couples it from the snooping process allowing it to be faster.
Again, in general, most all modern high-end (e.g. not targeted at embedded) processors have a write-through policy for the L1 cache, and a write-back policy for the lower level caches. There are several reasons for this. Since in this class of processors L2 caches are almost exclusively on-chip and generally quite fast the penalties from having L1 write-through are not the major consideration. Further, since L1 sizes are small, pools of written data unlikely to be read in the future could cause pollution of the limited L1 resource. Additionally, a write-through L1 does not have to be concerned if it has outstanding dirty data, hence can pass the extra coherency logic to the L2 (which, as we mentioned, already has a larger part to play in cache coherency).
Much of the time of a modern processor is spent waiting for much slower devices in the memory hierarchy to deliver data for processing.
Thus strategies to keep the pipeline of the processor full are paramount. One strategy is to include enough registers and state logic such that two instruction streams can be processed at the same time. This makes one CPU look for all intents and purposes like two CPUs.
While each CPU has its own registers, they still have to share the core logic, cache and input and output bandwidth from the CPU to memory. So while two instruction streams can keep the core logic of the processor busier, the performance increase will not be as great has having two physically separate CPUs. Typically the performance improvement is below 20% (XXX check), however it can be drastically better or worse depending on the workloads.
With increased ability to fit more and more transistors on a chip, it became possible to put two or more processors in the same physical package. Most common is dual-core, where two processor cores are in the same chip. These cores, unlike hyperthreading, are full processors and so appear as two physically separate processors a la a SMP system.
While generally the processors have their own L1 cache, they do have to share the bus connecting to main memory and other devices. Thus performance is not as great as a full SMP system, but considerably better than a hyperthreading system (in fact, each core can still implement hyperthreading for an additional enhancement).
Multi core processors also have some advantages not performance related. As we mentioned, external physical buses between processors have physical limits; by containing the processors on the same piece of silicon extremely close to each other some of these problems can be worked around. The power requirements for multi core processors are much less than for two separate processors. This means that there is less heat needing to be dissipated which can be a big advantage in data centre applications where computers are packed together and cooling considerations can be considerable. By having the cores in the same physical package it makes muti-processing practical in applications where it otherwise would not be, such as laptops. It is also considerably cheaper to only have to produce one chip rather than two.
Many applications require systems much larger than the number of processors a SMP system can scale to. One way of scaling up the system further is a cluster.
A cluster is simply a number of individual computers which have some ability to talk to each other. At the hardware level the systems have no knowledge of each other; the task of stitching the individual computers together is left up to software.
Software such as MPI allow programmers to write their software and then "farm out" parts of the program to other computers in the system. For example, image a loop that executes several thousand times performing independent action (that is no iteration of the loop affects any other iteration). With four computers in a cluster, the software could make each computer do 250 loops each.
The interconnect between the computers varies, and may be as slow as an internet link or as fast as dedicated, special buses (Infiniband). Whatever the interconnect, however, it is still going to be further down the memory hierarchy and much, much slower than RAM. Thus a cluster will not perform well in a situation when each CPU requires access to data that may be stored in the RAM of another computer; since each time this happens the software will need to request a copy of the data from the other computer, copy across the slow link and into local RAM before the processor can get any work done.
However, many applications do not require this constant copying around between computers. One large scale example is SETI@Home, where data collected from a radio antenna is analysed for signs of Alien life. Each computer can be distributed a few minutes of data to analyse, and only needs report back a summary of what it found. SETI@Home is effectively a very large, dedicated cluster.
Another application is rendering of images, especially for special effects in films. Each computer can be handed a single frame of the movie which contains the wire-frame models, textures and light sources which needs to be combined (rendered) into the amazing special effects we now take for grained. Since each frame is static, once the computer has the initial input it does not need any more communication until the final frame is ready to be sent back and combined into the move. For example the block-buster Lord of the Rings had their special effects rendered on a huge cluster running Linux.
Non-Uniform Memory Access, more commonly abbreviated to NUMA, is almost the opposite of a cluster system mentioned above. As in a cluster system it is made up of individual nodes linked together, however the linkage between nodes is highly specialised (and expensive!). As opposed to a cluster system where the hardware has no knowledge of the linkage between nodes, in a NUMA system the software has no (well, less) knowledge about the layout of the system and the hardware does all the work to link the nodes together.
The term non uniform memory access comes from the fact that RAM may not be local to the CPU and so data may need to be accessed from a node some distance away. This obviously takes longer, and is in contrast to a single processor or SMP system where RAM is directly attached and always takes a constant (uniform) time to access.
With so many nodes talking to each other in a system, minimising the distance between each node is of paramount importance. Obviously it is best if every single node has a direct link to every other node as this minimises the distance any one node needs to go to find data. This is not a practical situation when the number of nodes starts growing into the hundreds and thousands as it does with large supercomputers; if you remember your high school maths the problem is basically a combination taken two at a time (each node talking to another), and will grow n!/2*(n-2)!.
To combat this exponential growth alternative layouts are used to trade off the distance between nodes with the interconnects required. One such layout common in modern NUMA architectures is the hypercube.
A hypercube has a strict mathematical definition (way beyond this discussion) but as a cube is a 3 dimensional counterpart of a square, so a hypercube is a 4 dimensional counterpart of a cube.

Above we can see the outer cube contains four 8 nodes. The maximum number of paths required for any node to talk to another node is 3. When another cube is placed inside this cube, we now have double the number of processors but the maximum path cost has only increased to 4. This means as the number of processors grow by 2n the maximum path cost grows only linearly.
Cache coherency can still be maintained in a NUMA system (this is referred to as a cache-coherent NUMA system, or ccNUMA). As we mentioned, the broadcast based scheme used to keep the processor caches coherent in an SMP system does not scale to hundreds or even thousands of processors in a large NUMA system. One common scheme for cache coherency in a NUMA system is referred to as a directory based model. In this model processors in the system communicate to special cache directory hardware. The directory hardware maintains a consistent picture to each processor; this abstraction hides the working of the NUMA system from the processor.
The Censier and Feautrier directory based scheme maintains a central directory where each memory block has a flag bit known as the valid bit for each processor and a single dirty bit. When a processor reads the memory into its cache, the directory sets the valid bit for that processor.
When a processor wishes to write to the cache line the directory needs to set the dirty bit for the memory block. This involves sending an invalidate message to those processors who are using the cache line (and only those processors whose flag are set; avoiding broadcast traffic).
After this should any other processor try to read the memory block the directory will find the dirty bit set. The directory will need to get the updated cache line from the processor with the valid bit currently set, write the dirty data back to main memory and then provide that data back to the requesting processor, setting the valid bit for the requesting processor in the process. Note that this is transparent to the requesting processor and the directory may need to get that data from somewhere very close or somewhere very far away.
Obviously having thousands of processors communicating to a single directory does also not scale well. Extensions to the scheme involve having a hierarchy of directories that communicate between each other using a separate protocol. The directories can use a more general purpose communications network to talk between each other, rather than a CPU bus, allowing scaling to much larger systems.
NUMA systems are best suited to the types of problems that require much interaction between processor and memory. For example, in weather simulations a common idiom is to divide the environment up into small "boxes" which respond in different ways (oceans and land reflect or store different amounts of heat, for example). As simulations are run, small variations will be fed in to see what the overall result is. As each box influences the surrounding boxes (e.g. a bit more sun means a particular box puts out more heat, affecting the boxes next to it) there will be much communication (contrast that with the individual image frames for a rendering process, each of which does not influence the other). A similar process might happen if you were modelling a car crash, where each small box of the simulated car folds in some way and absorbs some amount of energy.
Although the software has no directly knowledge that the underlying system is a NUMA system, programmers need to be careful when programming for the system to get maximum performance. Obviously keeping memory close to the processor that is going to use it will result in the best performance. Programmers need to use techniques such as profiling to analyse the code paths taken and what consequences their code is causing for the system to extract best performance.
The multi-level cache, superscalar multi-processor architecture brings with it some interesting issues relating to how a programmer sees the processor running code.
Imagine program code is running on two processors simultaneously, both processors sharing effectively one large area of memory. If one processor issues a store instruction, to put a register value into memory, when can it be sure that the other processor does a load of that memory it will see the correct value?
In the simplest situation the system could guarantee that if a program executes a store instruction, any subsequent load instructions will see this value. This is referred to as strict memory ordering, since the rules allow no room for movement. You should be starting to realise why this sort of thing is a serious impediment to performance of the system.
Much of the time, the memory ordering is not required to be so strict. The programmer can identify points where they need to be sure that all outstanding operations are seen globally, but in between these points there may be many instructions where the semantics are not important.
Take, for example, the following situation.
1 typedef struct {
int a;
int b;
} a_struct;
5
/*
* Pass in a pointer to be allocated as a new structure
*/
void get_struct(a_struct *new_struct)
10 {
void *p = malloc(sizeof(a_struct));
/* We don't particularly care what order the following two
* instructions end up acutally executing in */
15 p->a = 100;
p->b = 150;
/* However, they must be done before this instruction.
* Otherwise, another processor who looks at the value of p
20 * could find it pointing into a structure whose values have
* not been filled out.
*/
new_struct = p;
}
25
In this example, we have two stores that can be done in any particular order, as it suits the processor. However, in the final case, the pointer must only be updated once the two previous stores are known to have been done. Otherwise another processor might look at the value of p, follow the pointer to the memory, load it, and get some completely incorrect value!
To indicate this, loads and stores have to have semantics that describe what behaviour they must have. Memory semantics are described in terms of fences that dictate how loads and stores may be reordered around the load or store.
By default, a load or store can be re-ordered anywhere.
Acquire semantics is like a fence that only allows load and stores to move downwards through it. That is, when this load or store is complete you can be guaranteed that any later load or stores will see the value (since they can not be moved above it).
Release semantics is the opposite, that is a fence that allows any load or stores to be done before it (move upwards), but nothing before it to move downwards past it. Thus, when load or store with release semantics is processed, you can be store that any earlier load or stores will have been complete.
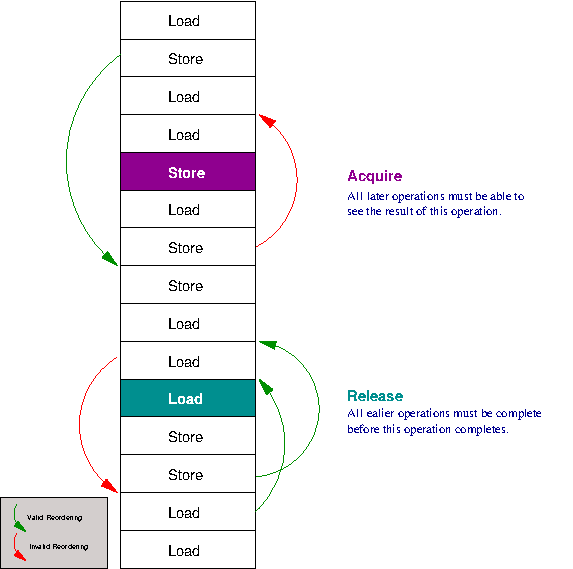
A full memory fence is a combination of both; where no loads or stores can be reordered in any direction around the current load or store.
The strictest memory model would use a full memory fence for every operation. The weakest model would leave every load and store as a normal re-orderable instruction.
Different processors implement different memory models.
The x86 (and AMD64) processor has a quite strict memory model; all stores have release semantics (that is, the result of a store is guaranteed to be seen by any later load or store) but all loads have normal semantics. lock prefix gives memory fence.
Itanium allows all load and stores to be normal, unless explicitly told. XXX
Knowing the memory ordering requirements of each architecture is not practical for all programmers, and would make programs difficult to port and debug across different processor types.
Programmers use a higher level of abstraction called locking to allow simultaneous operation of programs when there are multiple CPUs.
When a program acquires a lock over a piece of code, no other processor can obtain the lock until it is released. Before any critical pieces of code, the processor must attempt to take the lock; if it can not have it, it does not continue.
You can see how this is tied into the naming of the memory ordering semantics in the previous section. We want to ensure that before we acquire a lock, no operations that should be protected by the lock are re-ordered before it. This is how acquire semantics works.
Conversely, when we release the lock, we must be sure that every operation we have done whilst we held the lock is complete (remember the example of updating the pointer previously?). This is release semantics.
There are many software libraries available that allow programmers to not have to worry about the details of memory semantics and simply use the higher level of abstraction of lock() and unlock().
Locking schemes make programming more complicated, as it is possible to deadlock programs. Imagine if one processor is currently holding a lock over some data, and is currently waiting for a lock for some other piece of data. If that other processor is waiting for the lock the first processor holds before unlocking the second lock, we have a deadlock situation. Each processor is waiting for the other and neither can continue without the others lock.
Often this situation arises because of a subtle race condition; one of the hardest bugs to track down. If two processors are relying on operations happening in a specific order in time, there is always the possibility of a race condition occurring. A gamma ray from an exploding star in a different galaxy might hit one of the processors, making it skip a beat, throwing the ordering of operations out. What will often happen is a deadlock situation like above. It is for this reason that program ordering needs to be ensured by semantics, and not by relying on one time specific behaviours. (XXX not sure how i can better word that).
A similar situation is the opposite of deadlock, called livelock. One strategy to avoid deadlock might be to have a "polite" lock; one that you give up to anyone who asks. This politeness might cause two threads to be constantly giving each other the lock, without either ever taking the lock long enough to get the critical work done and be finished with the lock (a similar situation in real life might be two people who meet at a door at the same time, both saying "no, you first, I insist". Neither ends up going through the door!).
Underneath, there are many different strategies for implementing the behaviour of locks.
A simple lock that simply has two states - locked or unlocked, is referred to as a mutex (short for mutual exclusion; that is if one person has it the other can not have it).
There are, however, a number of ways to implement a mutex lock. In the simplest case, we have what its commonly called a spinlock. With this type of lock, the processor sits in a tight loop waiting to take the lock; equivalent to it saying "can I have it now" constantly much as a young child might ask of a parent.
The problem with this strategy is that it essentially wastes time. Whilst the processor is sitting constantly asking for the lock, it is not doing any useful work. For locks that are likely to be only held locked for a very short amount of time this may be appropriate, but in many cases the amount of time the lock is held might be considerably longer.
Thus another strategy is to sleep on a lock. In this case, if the processor can not have the lock it will start doing some other work, waiting for notification that the lock is available for use (we see in future chapters how the operating system can switch processes and give the processor more work to do).
A mutex is however just a special case of a semaphore, famously invented by the Dutch computer scientist Dijkstra. In a case where there are multiple resources available, a semaphore can be set to count accesses to the resources. In the case where the number of resources is one, you have a mutex. The operation of semaphores can be detailed in any algorithms book.
These locking schemes still have some problems however. In many cases, most people only want to read data which is updated only rarely. Having all the processors wanting to only read data require taking a lock can lead to lock contention where less work gets done because everyone is waiting to obtain the same lock for some data.
Explain what it is.


