5.6: Scheduling
- Page ID
- 77136
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A running system has many processes, maybe even into the hundreds or thousands. The part of the kernel that keeps track of all these processes is called the scheduler because it schedules which process should be run next.
Scheduling algorithms are many and varied. Most users have different goals relating to what they want their computer to do, so this affects scheduling decisions. For example, for a desktop PC you want to make sure that your graphical applications for your desktop are given plenty of time to run, even if system processes take a little longer. This will increase the responsiveness the user feels, as their actions will have more immediate responses. For a server, you might want your web server application to be given priority.
People are always coming up with new algorithms, and you can probably think of your own fairly easily. But there are a number of different components of scheduling.
Scheduling strategies can broadly fall into two categories
- Co-operative scheduling is where the currently running process voluntarily gives up executing to allow another process to run. The obvious disadvantage of this is that the process may decide to never give up execution, probably because of a bug causing some form of infinite loop, and consequently nothing else can ever run.
- Preemptive scheduling is where the process is interrupted to stop it to allow another process to run. Each process gets a time-slice to run in; at the point of each context switch a timer will be reset and will deliver and interrupt when the time-slice is over.
We know that the hardware handles the interrupt independently of the running process, and so at this point control will return to the operating system. At this point, the scheduler can decide which process to run next.
This is the type of scheduling used by all modern operating systems.
Some processes need to know exactly how long their time-slice will be, and how long it will be before they get another time-slice to run. Say you have a system running a heart-lung machine; you don't want the next pulse to be delayed because something else decided to run in the system!
Hard realtime systems make guarantees about scheduling decisions like the maximum amount of time a process will be interrupted before it can run again. They are often used in life critical applications like medical, aircraft and military applications.
Soft realtime is a variation on this, where guarantees aren't as strict but general system behaviour is predictable. Linux can be used like this, and it is often used in systems dealing with audio and video. If you are recording an audio stream, you don't want to be interrupted for long periods of time as you will loose audio data which can not be retrieved.
UNIX systems assign each process a nice value. The scheduler looks at the nice value and can give priority to those processes that have a higher "niceness".
The Linux scheduler has and is constantly undergoing many changes as new developers attempt to improve its behaviour.
The current scheduler is known as the O(1) scheduler, which refers to the property that no matter how many processes the scheduler has to choose from, it will choose the next one to run in a constant amount of time[17].
Previous incarnations of the Linux scheduler used the concept of goodness to determine which process to run next. All possible tasks are kept on a run queue, which is simply a linked list of processes which the kernel knows are in a "runnable" state (i.e. not waiting on disk activity or otherwise asleep). The problem arises that to calculate the next process to run, every possible runnable process must have its goodness calculated and the one with the highest goodness ``wins''. You can see that for more tasks, it will take longer and longer to decide which processes will run next.
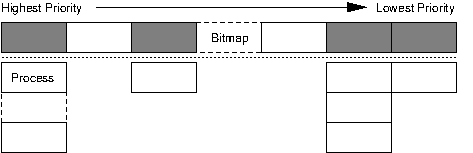
In contrast, the O(1) scheduler uses a run queue structure as shown above. The run queue has a number of buckets in priority order and a bitmap that flags which buckets have processes available. Finding the next process to run is a matter of reading the bitmap to find the first bucket with processes, then picking the first process off that bucket's queue. The scheduler keeps two such structures, an active and expired array for processes that are runnable and those which have utilised their entire time slice respectively. These can be swapped by simply modifying pointers when all processes have had some CPU time.
The really interesting part, however, is how it is decided where in the run queue a process should go. Some of the things that need to be taken into account are the nice level, processor affinity (keeping processes tied to the processor they are running on, since moving a process to another CPU in a SMP system can be an expensive operation) and better support for identifying interactive programs (applications such as a GUI which may spend much time sleeping, waiting for user input, but when the user does get around to interacting with it wants a fast response).
[17] Big-O notation is a way of describing how long an algorithm takes to run given increasing inputs. If the algorithm takes twice as long to run for twice as much input, this is increasing linearly. If another algorithm takes four times as long to run given twice as much input, then it is increasing exponentially. Finally if it takes the same amount of time now matter how much input, then the algorithm runs in constant time. Intuitively you can see that the slower the algorithm grows for more input, the better it is. Computer science text books deal with algorithm analysis in more detail.


