3.3.1: Representing sets
- Page ID
- 10724
A set is determined by its elements. Given a set A and an entity x, the fundamental question is, does x belong to A or not? If we know the answer to this question for each possible x, then we know the set. For a given x, the answer to the question, “Is x a member of A”, is either yes or no. The answer can be encoded by letting 1 stand for yes and 0 stand for no. The answer, then, is a single bit, that is, a value that can be either zero or one. To represent the set A as a string of zeros and ones, we could use one bit for each possible member of A. If a possible member x is in the set, then the corresponding bit has the value one. If x is not in the set, then the corresponding bit has the value zero.
Now, in cases where the number of possible elements of the set is very large or infinite, it is not practical to represent the set in this way. It would require too many bits, perhaps an infinite number. In such cases, some other representation for the set can be used. However, suppose we are only interested in subsets of some specified small set. Since this set plays the role of a universal set, let’s call it U. To represent a subset of U, we just need one bit for each member of U. If the number of members of U is n, then a subset of U is represented by a string of n zeros and ones. Furthermore, every string of n zeros and ones determines a subset of U, namely that subset that contains exactly the elements of U that correspond to ones in the string. You know by now from Computer Organisation that a string of n zeros and ones is called an n-bit binary number. So, we see that if U is a set with n elements, then the subsets of U correspond to n-bit binary numbers.
To make things more definite, let U be the set {0, 1, 2, . . . , 31}. This set consists of the 32 integers between 0 and 31, inclusive. Then each subset of U can be represented by a 32-bit binary number. We use 32 bits because most computer languages can work directly with 32-bit numbers. For example, the programming languages Java has a data type named int. A value of type int is a 32-bit binary number.2 Before we get a definite correspondence between subsets of U and 32-bit numbers, we have to decide which bit in the number will correspond to each member of U. Following tradition, we assume that the bits are numbered from right to left. That is, the rightmost bit corresponds to the element 0 in U, the second bit from the right corresponds to 1, the third bit from the right to 2, and so on. For example, the 32-bit number
1000000000000000000001001110110
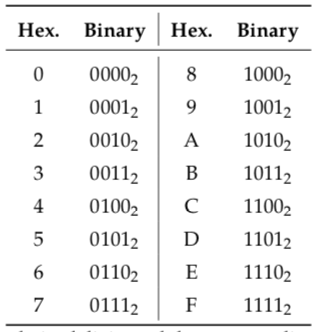
Figure 4.6: The 16 hexadecimal digits and the corresponding binary numbers. Each hexadecimal digit corresponds to a 4-bit binary number. Longer binary numbers can be written using two or more hexadecimal digits. For example, \(101000011111_{2}=0 x A 1 F\)
corresponds to the subset {1, 2, 4, 5, 6, 9, 31}. Since the leftmost bit of the number is 1, the number 31 is in the set; since the next bit is 0, the number 30 is not in the set; and so on. From now on, I will write binary numbers with a subscript of 2 to avoid confusion
with ordinary numbers. Furthermore, I will often leave out leading zeros. For example, 11012 is the binary number that would be written out in full as
00000000000000000000000000001101
and which corresponds to the set {0, 2, 3}. On the other hand 1101 represents the ordinary number one thousand one hundred and one.
Even with this notation, it can be very annoying to write out long binary numbers— and almost impossible to read them. So binary numbers are never written out as sequences of zeros and ones in computer programs. An alternative is to use hexadecimal numbers. Hexadecimal numbers are written using the sixteen symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F. These symbols are knows as the hexadecimal digits. Each hexadecimal digit corresponds to a 4-bit binary number, as shown in Figure 4.6. To represent a longer binary number, several hexadecimal digits can be strung together. For example, the hexadecimal number C7 represents the binary number 110001112. In Java and many related languages, a hexadecimal number is written with the prefix 0x. Thus, the hexa- decimal number C7 would appear in the program as 0xC7. I will follow the same convention here. Any 32-bit binary number can be written using eight hexadecimal digits (or fewer if leading zeros are omitted). Thus, subsets of {0, 1, 2, . . . , 31} correspond to 8-digit hexadecimal numbers. For example, the subset {1, 2, 4, 5, 6, 9, 31} corresponds to 0x80000276, which represents the binary number 10000000000000000000010011101102. Similarly, 0xFF corresponds to {0, 1, 2, 3, 4, 5, 6, 7} and 0x1101 corresponds to the binary number 00010001000000012 and to the set {0, 8, 12}.
Now, if you have worked with binary numbers or with hexadecimal numbers, you know that they have another, more common interpretation. They represent ordinary integers. Just as 342 represents the integer \(3 \cdot 10^{2}+4 \cdot 10^{1}+2 \cdot 10^{0}\), the binary number \(1101_{2}\) represents the integer \(1 \cdot 2^{3}+1 \cdot 2^{2}+0 \cdot 2^{1}+1 \cdot 2^{0},\) or 13. When used in this way, binary numbers are known as base-2 numbers, just as ordinary numbers are base-10 numbers. Hexadecimal numbers can be interpreted as base-16 numbers. For example, 0x3C7 represents the integer \(3 \cdot 16^{2}+12 \cdot 16^{1}+7 \cdot 16^{0},\) or 874. So, does 11012 really represent the integer 13, or does it represent the set {0, 2, 3} ? The answer is that to a person, 11012 can represent either. Both are valid interpretations, and the only real question is which interpretation is useful in a given circumstance. On the other hand, to the computer, 11012 doesn’t represent anything. It’s just a string of bits, and the computer manipulates the bits according to its program, without regard to their interpretation.
Of course, we still have to answer the question of whether it is ever useful to interpret strings of bits in a computer as representing sets.

