3.3.2: Computing with sets
- Page ID
- 10725
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)If all we could do with sets were to ‘represent’ them, it wouldn’t be very useful. We need to be able to compute with sets. That is, we need to be able to perform set operations such as union and complement.
Many programming languages provide operators that perform set operations. In Java and related languages, the operators that perform union, intersection, and comple- ment are written as | , &, and ~. For example, if x and y are 32-bit integers representing two subsets, X and Y, of {0, 1, 2, . . . , 31}, then x | y is a 32-bit integer that represents the set X ∪ Y. Similarly, x & y represents the set X ∩ Y, and ~x represents the complement,X.
The operators | , &, and ~ are called bitwise logical operators because of the way they operate on the individual bits of the numbers to which they are applied. If 0 and 1 are interpreted as the logical values false and true, then the bitwise logical operators perform the logical operations ∨, ∧, and ¬ on individual bits. To see why this is true, let’s look at the computations that these operators have to perform.
Let k be one of the members of {0,1,2,...,31}. In the binary numbers x, y, x|y,x & y, and ~x, the number k corresponds to the bit in position k. That is, k is in the set represented by a binary number if and only if the bit in position k in that binary number is 1. Considered as sets, x & y is the intersection of x and y, so k is a member of the set represented by x & y if and only if k is a member of both of the sets represented by x and y. That is, bit k is 1 in the binary number x&y if and only if bit k is 1 in x and bit k is 1 in y. When we interpret 1 as true and 0 as false, we see that bit k of x&y is computed by applying the logical ‘and’ operator, ∧, to bit k of x and bit k of y. Similarly, bit k of x | y is computed by applying the logical ‘or’ operator, ∨, to bit k of x and bit k of y. And bit kof ~x is computed by applying the logical ‘not’ operator, ¬, to bit k of x. In each case, the logical operator is applied to each bit position separately. (Of course, this discussion is just a translation to the language of bits of the definitions of the set operations in terms of logical operators: A∩B = {x|x ∈ A∧x ∈ B}, A∪B = {x|x ∈ A∨x ∈ B}, and A = {x ∈ U | ¬(x ∈ A)}.)
For example, consider the binary numbers 10110102 and 101112, which represent the sets {1, 3, 4, 6} and {0, 1, 2, 4}. Then 10110102 & 101112 is 100102. This binary number represents the set {1, 4}, which is the intersection {1, 3, 4, 6} ∩ {0, 1, 2, 4}. It’s easier to see what’s going on if we write out the computation in columns, the way you probably first learned to do addition:
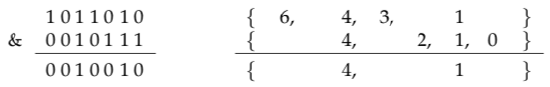
Note that in each column in the binary numbers, the bit in the bottom row is computed as the logical ‘and’ of the two bits that lie above it in the column. I’ve written out the sets that correspond to the binary numbers to show how the bits in the numbers correspond to the presence or absence of elements in the sets. Similarly, we can see how the union of two sets is computed as a bitwise ‘or’ of the corresponding binary numbers.
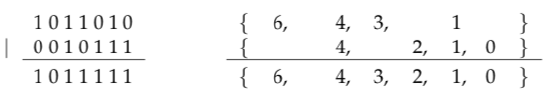
The complement of a set is computed using a bitwise ‘not’ operation. Since we are work- ing with 32-bit binary numbers, the complement is taken with respect to the universal set {0,1,2,...,31}. So, for example,
\(-1011010_{2}=111111111111111111111110100101_{2}\)
Of course, we can apply the operators &, | , and ~ to numbers written in hexadecimal form, or even in ordinary, base-10 form. When doing such calculations by hand, it is probably best to translate the numbers into binary form. For example,
0xAB7 & 0x168E = \(101010110111_{2} \& 101101000110_{2}\)
= \(0001010000110_{2}\)
= 0x286
When computing with sets, it is sometimes necessary to work with individual ele- ments. Typical operations include adding an element to a set, removing an element from a set, and testing whether an element is in a set. However, instead of working with an element itself, it’s convenient to work with the set that contains that element as its only member. For example, testing whether 5 ∈ A is the same as testing whether \(\{5\} \cap A \neq \varnothing .\) The set \(\{5\}\) is represented by the binary number \(100000_{2}\) or by the hexadecimal number 0x20. Suppose that the set A is represented by the number x. Then, testing whether 5\(\in A\) is equivalent to testing whether \(0 \times 20 \& x \neq 0 .\) Similarly, the set A ∪ {5}, which is obtained by adding 5 to A, can be computed as x | 0x20. The setA ∖ {5}, which is the set obtained by removing 5 from A if it occurs in A, is represented by x & ~0x20.
The sets {0}, {1}, {2}, {3}, {4}, {5}, {6}, ..., {31} are represented by the hexadecimal numbers 0x1, 0x2, 0x4, 0x8, 0x10, 0x20, ..., 0x80000000. In typical computer applications, some of these numbers are given names, and these names are thought of as names for the possible elements of a set (although, properly speaking, they are names for sets con- taining those elements). Suppose, for example, that a, b, c, and d are names for four of the numbers from the above list. Then a | c is the set that contains the two elements corresponding to the numbers a and c. If x is a set, then x&~d is the set obtained by removing \(d\) from \(x .\) And we can test whether \(b\) is in \(x\) by testing if \(x \& b \neq 0\).
Here is an actual example, which is used in the Apple Mac operating systems (ma- cOS). Characters can be printed or displayed on the screen in various sizes and styles. Afont is a collection of pictures of characters in a particular size and style. On the Mac, a basic font can be modified by specifying any of the following style attributes: bold, italic,underline, outline, shadow, condense, and extend. The style of a font is a subset of this set of attributes. A style set can be specified by or-ing together individual attributes. For ex- ample, an underlined, bold, italic font has style set underline | bold | italic. For a plain font, with none of the style attributes set, the style set is the empty set, which is represented by the number zero.
The Java programming language uses a similar scheme to specify style attributes for fonts, but currently there are only two basic attributes, Font.BOLD and Font.ITALIC. A more interesting example in Java is provided by event types. An event in Java represents some kind of user action, such as pressing a key on the keyboard. Events are associated with ‘components’ such as windows, push buttons, and scroll bars. Components can be set to ignore a given type of event. We then say that that event type is disabled for that component. If a component is set to process events of a given type, then that event type is said to be enabled. Each component keeps track of the set of event types that are currently enabled. It will ignore any event whose type is not in that set. Each event type has an associated constant with a name such as AWTEvent.MOUSE_EVENT_MASK. These constants represent the possible elements of a set of event types. A set of event types can be specified by or-ing together a number of such constants. If c is a component andx is a number representing a set of event types, then the command ‘c.enableEvents(x)’ enables the events in the set x for the component c. If y represents the set of event types that were already enabled for c, then the effect of this command is to replace y with the union, y | x. Another command, “c.disableEvents(x)”, will disable the event types in x for the component c. It does this by replacing the current set, y, with y & ~x.
Exercises
1. Suppose that the numbers x and y represent the sets A and B. Show that the set A ∖ B is represented by x & (~y).
2. Write each of the following binary numbers in hexadecimal:
a. \(10110110_{2}\) b. \(10_{2}\) c. \(111100001111_{2}\) d. \(101001_{2}\)
3. Write each of the following hexadecimal numbers in binary:
a) 0x123 b) 0xFADE c) 0x137F d) 0xFF11
4. Give the value of each of the following expressions as a hexadecimal number:
a) 0x73 | 0x56A b) ~0x3FF0A2FF c) (0x44 | 0x95) & 0xE7 d) 0x5C35A7 & 0xFF00
e) 0x5C35A7 & ~0xFF00 f) ~(0x1234 & 0x4321)
5. Find a calculator (or a calculator program on a computer) that can work with hexadecimal numbers. Write a short report explaining how to work with hexadecimal numbers on that calculator. You should explain, in particular, how the calculator can be used to do the previous problem.
6. This question assumes that you know how to add binary numbers. Suppose x and y are binary numbers. Under what circumstances will the binary numbers x + y and x | y be the same?
7. In addition to hexadecimal numbers, the programming languages Java, C, and C++ supportoctal numbers. Look up and report on octal numbers in Java, C, or C++. Explain what octal numbers are, how they are written, and how they are used.
8. In the Unix (and Linux, macOS, ...) operating system, every file has an associated set of per- missions, which determine who can use the file and how it can be used. The set of permissions for a given file is represented by a nine-bit binary number. This number is sometimes written as an octal number. Research and report on the Unix systems of permissions. What set of permissions is represented by the octal number 752? by the octal number 622? Explain what is done by the Unix commands chmod g+rw filename and chmod o-w filename in terms of sets.
9. Most modern programming languages have a boolean data type that has the values true andfalse. The usual logical and, or, and not operators on boolean values are represented in Java, C and C++ by the operators &&, | |, and !. C and C++ (but not Java) allow integer values to be used in places where boolean values are expected. In this case, the integer zero represents the boolean value false while any non-zero integer represents the boolean value true. This means that if x and y are integers, then both x & y and x && y are valid expressions, and both can be considered to represent boolean values. Do the expressions x & y and x && y always represent the same boolean value, for any integers x and y? Do the expressions x | y and x | | y always represent the same boolean values? Explain your answers.
10. Suppose that you, as a programmer, want to write a subroutine that will open a window on the computer’s screen. The window can have any of the following options: a close box, a zoom box, a resize box, a minimize box, a vertical scroll bar, a horizontal scroll bar. Design a scheme whereby the options for the window can be specified by a single parameter to the subroutine. The parameter should represent a set of options. How would you use your subroutine to open a window that has a close box and both scroll bars and no other options? Inside your subroutine, how would you determine which options have been specified for the window?

