3.8: Relational Databases
- Page ID
- 10911
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)One of the major uses of computer systems is to store and manipulate collections of data. A database is a collection of data that has been organized so that it is possible to add and delete information, to update the data that it contains, and to retrieve specified parts of the data. A Database Management System, or DBMS, is a computer program that makes it possible to create and manipulate databases. A DBMS must be able to accept and process commands that manipulate the data in the databases that it manages. These commands are called queries, and the languages in which they are written are called query languages. A query language is a kind of specialized programming language.
There are many different ways that the data in a database could be represented. Different DBMS’s use various data representations and various query languages. However, data is most commonly stored in relations. A relation in a database is a relation in the mathematical sense. That is, it is a subset of a cross product of sets. A database that stores its data in relations is called a relational database. The query language for most relational database management systems is some form of the language known as Structured Query Language, or SQL. In this section, we’ll take a very brief look at SQL, relational databases, and how they use relations.
You’ll learn more about databases in the courses Web & Database Technology and Information & Data Management.
A relation is just a subset of a cross product of sets. Since we are discussing computer representation of data, the sets are data types. As in Section 4.5, we’ll use data type names such as int and string to refer to these sets. A relation that is a subset of the cross product int × int × string would consist of ordered 3-tuples such as (17, 42, “hike”). In a relational database, the data is stored in the form of one or more such relations. The relations are called tables, and the tuples that they contain are called rows or records.
As an example, consider a lending library that wants to store data about its members, the books that it owns, and which books the members have out on loan. This data could be represented in three tables, as illustrated in Figure 4.8. The relations are shown as tables rather than as sets of ordered tuples, but each table is, in fact, a relation. The rows of the table are the tuples. The Members table, for example, is a subset of int × string ×string × string, and one of the tuples is (1782, “Smit, Johan”, “107 Main St”, “New York, NY”). A table does have one thing that ordinary relations in mathematics do not have. Each column in the table has a name. These names are used in the query language to manipulate the data in the tables.
The data in the Members table is the basic information that the library needs in order to keep track of its members, namely the name and address of each member. A member also has a MemberID number, which is presumably assigned by the library. Two different members can’t have the same MemberID, even though they might have the same name or the same address. The MemberID acts as a primary key for the Members table. A given value of the primary key uniquely identifies one of the rows of the table. Similarly, the BookID in the Books table is a primary key for that table. In the Loans table, which holds information about which books are out on loan to which members, a MemberID unambiguously identifies the member who has a given book on loan, and the BookIDsays unambiguously which book that is. Every table has a primary key, but the key can consist of more than one column. The DBMS enforces the uniqueness of primary keys. That is, it won’t let users make a modification to the table if it would result in two rows having the same primary key.
The fact that a relation is a set—a set of tuples—means that it can’t contain the same tuple more than once. In terms of tables, this means that a table shouldn’t contain two identical rows. But since no two rows can contain the same primary key, it’s impossible
for two rows to be identical. So tables are in fact relations in the mathematical sense.
The library must have a way to add and delete members and books and to make a record when a book is borrowed or returned. It should also have a way to change the address of a member or the due date of a borrowed book. Operations such as these are performed using the DBMS’s query language. SQL has commands named INSERT,DELETE, and UPDATE for performing these operations. The command for adding Barack Obama as a member of the library with MemberID 999 would be
INSERT INTO Members
VALUES (999, "Barack Obama",
"1600 Pennsylvania Ave", "Washington, DC")
When it comes to deleting and modifying rows, things become more interesting because it’s necessary to specify which row or rows will be affected. This is done by specifying a condition that the rows must fulfill. For example, this command will delete the member with ID 4277:
DELETE FROM Members
WHERE MemberID = 4277
It’s possible for a command to affect multiple rows. For example,
DELETE FROM Members
WHERE Name = "Smit, Johan"
would delete every row in which the name is “Smit, Johan”. The update command also specifies what changes are to be made to the row:
UPDATE Members
SET Address="19 South St", City="Hartford, CT"
WHERE MemberID = 4277
Of course, the library also needs a way of retrieving information from the database. SQL provides the SELECT command for this purpose. For example, the query
SELECT Name, Address
FROM Members
WHERE City = "New York, NY"
asks for the name and address of every member who lives in New York City. The last line of the query is a condition that picks out certain rows of the “Members” relation, namely all the rows in which the City is “New York, NY”. The first line specifies which data from those rows should be retrieved. The data is actually returned in the form of a table. For example, given the data in Figure 4.8, the query would return this table:

The table returned by a SELECT query can even be used to construct more complex quer- ies. For example, if the table returned by SELECT has only one column, then it can be used with the IN operator to specify any value listed in that column. The following query will find the BookID of every book that is out on loan to a member who lives in New York City:
SELECT BookID
FROM Loans
WHERE MemberID IN (SELECT MemberID
FROM Members
WHERE City = "New York, NY")
More than one table can be listed in the FROM part of a query. The tables that are listed are joined into one large table, which is then used for the query. The large table is essentially the cross product of the joined tables, when the tables are understood as sets of tuples. For example, suppose that we want the titles of all the books that are out on loan to members who live in New York City. The titles are in the Books table, while information about loans is in the Loans table. To get the desired data, we can join the tables and extract the answer from the joined table:
SELECT Title
FROM Books, Loans
WHERE MemberID IN (SELECT MemberID
FROM Members
WHERE City = "New York, NY")
In fact, we can do the same query without using the nested SELECT. We need one more bit of notation: If two tables have columns that have the same name, the columns can be named unambiguously by combining the table name with the column name. For ex- ample, if the Members table and Loans table are both under discussion, then the MemberIDcolumns in the two tables can be referred to as Members.MemberID and Loans.MemberID. So, we can say:
SELECT Title
FROM Books, Loans
WHERE City ="New York, NY"
AND Members.MemberID = Loans.MemberID
This is just a sample of what can be done with SQL and relational databases. The conditions in WHERE clauses can get very complicated, and there are other operations besides the cross product for combining tables. The database operations that are needed to complete a given query can be complex and time-consuming. Before carrying out a query, the DBMS tries to optimize it. That is, it manipulates the query into a form that can be carried out most efficiently. The rules for manipulating and simplifying queries form an algebra of relations, and the theoretical study of relational databases is in large part the study of the algebra of relations.
Exercises
1. Using the library database from Figure 4.8, what is the result of each of the following SQL
commands?
- a) SELECT Name, Address
FROM Members 4WHERE Name = "Smit, Johan"-
a) SELECT Name, Address FROM Members WHERE Name = "Smit, Johan" -
b) DELETE FROM Books WHERE Author = "Isaac Asimov" -
c) UPDATE Loans SET DueDate = "20 November" WHERE BookID = 221d) SELECT Title FROM Books, Loans WHERE Books.BookID = Loans.BookID -
e) DELETE FROM Loans WHERE MemberID IN (SELECT MemberID FROM Members WHERE Name = "Lee, Joseph")
-
- Using the library database from Figure 4.8, write an SQL command to do each of the following database manipulations:
- a) Find the BookID of every book that is due on 1 November 2010.
- b) Change the DueDate of the book with BookID 221 to 15 November 2010.
- c) Change the DueDate of the book with title “Summer Lightning” to 14 November 2010. Use a nested SELECT.
- d) Find the name of every member who has a book out on loan. Use joined tables in the FROM clause of a SELECT command.
- Suppose that a university colleges wants to use a database to store information about its students, the courses that are offered in a given term, and which students are taking which courses. Design tables that could be used in a relational database for representing this data. Then write SQL commands to do each of the following database manipulations. (You should design your tables so that they can support all these commands.)
- Enroll the student with ID number 1928882900 in “English 260”.
- Remove “Johan Smit” from “Biology 110”.
- Remove the student with ID number 2099299001 from every course in which that stu- dent is enrolled.
- Find the names and addresses of the students who are taking “Computer Science 229”.
- Cancel the course “History 101”.


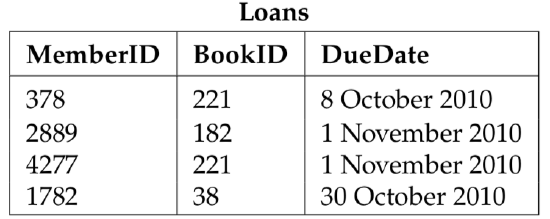
Figure 4.8: Tables that could be part of a relational database. Each table has a name, shown above the table. Each column in the table also has a name, shown in the top row of the table. The remaining rows hold the data.

