3.1: What a Compiler Does
- Page ID
- 13428
Introduction
The goal of an optimizing compiler is the efficient translation of a higher-level language into the fastest possible machine language that accurately represents the high-level language source. What makes a representation good is: it gives the correct answers, and it executes quickly.
Naturally, it makes no difference how fast a program runs if it doesn’t produce the right answers.1 But given an expression of a program that executes correctly, an optimizing compiler looks for ways to streamline it. As a first cut, this usually means simplifying the code, throwing out extraneous instructions, and sharing intermediate results between statements. More advanced optimizations seek to restructure the program and may actually make the code grow in size, though the number of instructions executed will (hopefully) shrink.
When it comes to finally generating machine language, the compiler has to know about the registers and rules for issuing instructions. For performance, it needs to understand the costs of those instructions and the latencies of machine resources, such as the pipelines. This is especially true for processors that can execute more than one instruction at a time. It takes a balanced instruction mix — the right proportion of floating-point, fixed point, memory and branch operations, etc. — to keep the machine busy.
Initially compilers were tools that allowed us to write in something more readable than assembly language. Today they border on artificial intelligence as they take our high-level source code and translate it into highly optimized machine language across a wide variety of single- and multiple-processor architectures. In the area of high performance computing, the compiler at times has a greater impact on the performance of our program than either the processor or memory architecture. Throughout the history of high performance computing, if we are not satisfied with the performance of our program written in a high-level language, we will gladly rewrite all or part of the program in assembly language. Thankfully, today’s compilers usually make that step unnecessary.
In this chapter we cover the basic operation of optimizing compilers. In a later chapter we will cover the techniques used to analyze and compile programs for advanced architectures such as parallel or vector processing systems. We start our look at compilers examining how the relationship between programmers and their compilers has changed over time.
History of Compilers
If you have been in high performance computing since its beginning in the 1950s, you have programmed in several languages during that time. During the 1950s and early 1960s, you programmed in assembly language. The constraint on memory and slow clock rates made every instruction precious. With small memories, overall program size was typically small, so assembly language was sufficient. Toward the end of the 1960s, programmers began writing more of their code in a high-level language such as FORTRAN. Writing in a high-level language made your work much more portable, reliable, and maintainable. Given the increasing speed and capacity of computers, the cost of using a high-level language was something most programmers were willing to accept. In the 1970s if a program spent a particularly large amount of time in a particular routine, or the routine was part of the operating system or it was a commonly used library, most likely it was written in assembly language.
During the late 1970s and early 1980s, optimizing compilers continued to improve to the point that all but the most critical portions of general-purpose programs were written in high-level languages. On the average, the compilers generate better code than most assembly language programmers. This was often because a compiler could make better use of hardware resources such as registers. In a processor with 16 registers, a programmer might adopt a convention regarding the use of registers to help keep track of what value is in what register. A compiler can use each register as much as it likes because it can precisely track when a register is available for another use.
However, during that time, high performance computer architecture was also evolving. Cray Research was developing vector processors at the very top end of the computing spectrum. Compilers were not quite ready to determine when these new vector instructions could be used. Programmers were forced to write assembly language or create highly hand-tuned FORTRAN that called the appropriate vector routines in their code. In a sense, vector processors turned back the clock when it came to trusting the compiler for a while. Programmers never lapsed completely into assembly language, but some of their FORTRAN started looking rather un-FORTRAN like. As the vector computers matured, their compilers became increasingly able to detect when vectorization could be performed. At some point, the compilers again became better than programmers on these architectures. These new compilers reduced the need for extensive directives or language extensions.2
The RISC revolution led to an increasing dependence on the compiler. Programming early RISC processors such as the Intel i860 was painful compared to CISC processors. Subtle differences in the way a program was coded in machine language could have a significant impact on the overall performance of the program. For example, a programmer might have to count the instruction cycles between a load instruction and the use of the results of the load in a computational instruction. As superscalar processors were developed, certain pairs of instructions could be issued simultaneously, and others had to be issued serially. Because there were a large number of different RISC processors produced, programmers did not have time to learn the nuances of wringing the last bit of performance out of each processor. It was much easier to lock the processor designer and the compiler writer together (hopefully they work for the same company) and have them hash out the best way to generate the machine code. Then everyone would use the compiler and get code that made reasonably good use of the hardware.
The compiler became an important tool in the processor design cycle. Processor designers had much greater flexibility in the types of changes they could make. For example, it would be a good design in the next revision of a processor to execute existing codes 10% slower than a new revision, but by recompiling the code, it would perform 65% faster. Of course it was important to actually provide that compiler when the new processor was shipped and have the compiler give that level of performance across a wide range of codes rather than just one particular benchmark suite.
Which Language To Optimize
It has been said, “I don’t know what language they will be using to program high performance computers 10 years from now, but we do know it will be called FORTRAN.” At the risk of inciting outright warfare, we need to discuss the strengths and weaknesses of languages that are used for high performance computing. Most computer scientists (not computational scientists) train on a steady diet of C, C++,3 or some other language focused on data structures or objects. When students encounter high performance computing for the first time, there is an immediate desire to keep programming in their favorite language. However, to get the peak performance across a wide range of architectures, FORTRAN is the only practical language.
When students ask why this is, usually the first answer is, “Because it has always been that way.” In one way this is correct. Physicists, mechanical engineers, chemists, structural engineers, and meteorologists do most programming on high performance computers. FORTRAN is the language of those fields. (When was the last time a computer science student wrote a properly working program that computed for a week?) So naturally the high performance computer vendors put more effort into making FORTRAN work well on their architecture.
This is not the only reason that FORTRAN is a better language, however. There are some fundamental elements that make C, C++, or any data structures-oriented language unsuitable for high performance programming. In a word, that problem is pointers. Pointers (or addresses) are the way good computer scientists construct linked lists, binary trees, binomial queues, and all those nifty data structures. The problem with pointers is that the effect of a pointer operation is known only at execution time when the value of the pointer is loaded from memory. Once an optimizing compiler sees a pointer, all bets are off. It cannot make any assumptions about the effect of a pointer operation at compile time. It must generate conservative (less optimized) code that simply does exactly the same operation in machine code that the high-level language described.
While the lack of pointers in FORTRAN is a boon to optimization, it seriously limits the programmer’s ability to create data structures. In some applications, especially highly scalable network-based applications, the use of good data structures can significantly improve the overall performance of the application. To solve this, in the FORTRAN 90 specification, pointers have been added to FORTRAN. In some ways, this was an attempt by the FORTRAN community to keep programmers from beginning to use C in their applications for the data structure areas of their applications. If programmers begin to use pointers throughout their codes, their FORTRAN programs will suffer from the same problems that inhibit optimization in C programs. In a sense FORTRAN has given up its primary advantage over C by trying to be more like C. The debate over pointers is one reason that the adoption rate of FORTRAN 90 somewhat slowed. Many programmers prefer to do their data structure, communications, and other bookkeeping work in C, while doing the computations in FORTRAN 77.
FORTRAN 90 also has strengths and weaknesses when compared to FORTRAN 77 on high performance computing platforms. FORTRAN 90 has a strong advantage over FORTRAN 77 in the area of improved semantics that enable more opportunities for advanced optimizations. This advantage is especially true on distributed memory systems on which data decomposition is a significant factor. (See Section 4.1.) However, until FORTRAN 90 becomes popular, vendors won’t be motivated to squeeze the last bit of performance out of FORTRAN 90.
So while FORTRAN 77 continues to be the mainstream language for high performance computing for the near future, other languages, like C and FORTRAN 90, have their limited and potentially increasing roles to play. In some ways the strongest potential challenger to FORTRAN in the long run may come in the form of a numerical tool set such as Matlab. However, packages such as Matlab have their own set of optimization challenges that must be overcome before they topple FORTRAN 77’s domination.
Optimizing Compiler Tour
We will start by taking a walk through an optimizing compiler to see one at work. We think it’s interesting, and if you can empathize with the compiler, you will be a better programmer; you will know what the compiler wants from you, and what it can do on its own.
Compilation Process
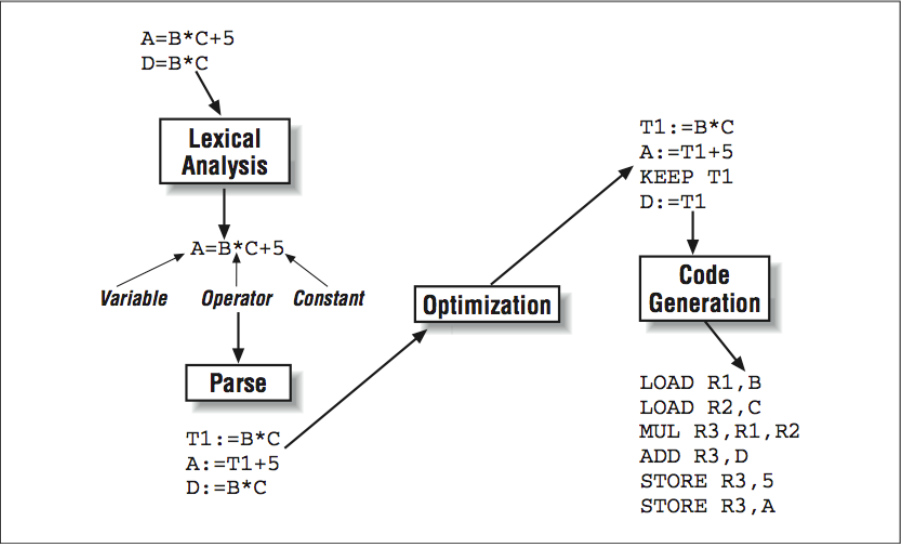
The compilation process is typically broken down into a number of identifiable steps, as shown in [Figure 1]. While not all compilers are implemented in exactly this way, it helps to understand the different functions a compiler must perform:
- A precompiler or preprocessor phase is where some simple textual manipulation of the source code is performed. The preprocessing step can be processing of include files and making simple string substitutions throughout the code.
- The lexical analysis phase is where the incoming source statements are decomposed into tokens such as variables, constants, comments, or language elements.
- The parsing phase is where the input is checked for syntax, and the compiler translates the incoming program into an intermediate language that is ready for optimization.
- One or more optimization passes are performed on the intermediate language.
- An object code generator translates the intermediate language into assembly code, taking into consideration the particular architectural details of the processor in question.
As compilers become more and more sophisticated in order to wring the last bit of performance from the processor, some of these steps (especially the optimization and code-generation steps) become more and more blurred. In this chapter, we focus on the traditional optimizing compiler, and in later chapters we will look more closely at how modern compilers do more sophisticated optimizations.
Intermediate Language Representation
Because we are most interested in the optimization of our program, we start our discussion at the output of the parse phase of the compiler. The parse phase output is in the form of an an intermediate language (IL) that is somewhere between a high-level language and assembly language. The intermediate language expresses the same calculations that were in the original program, in a form the compiler can manipulate more easily. Furthermore, instructions that aren’t present in the source, such as address expressions for array references, become visible along with the rest of the program, making them subject to optimizations too.
How would an intermediate language look? In terms of complexity, it’s similar to assembly code but not so simple that the definitions4 and uses of variables are lost. We’ll need definition and use information to analyze the flow of data through the program. Typically, calculations are expressed as a stream of quadruples — statements with exactly one operator, (up to) two operands, and a result.5 Presuming that anything in the original source program can be recast in terms of quadruples, we have a usable intermediate language. To give you an idea of how this works, We’re going to rewrite the statement below as a series of four quadruples:
A = -B + C * D / E
Taken all at once, this statement has four operators and four operands: /, *, +, and - (negate), and B, C, D, and E. This is clearly too much to fit into one quadruple. We need a form with exactly one operator and, at most, two operands per statement. The recast version that follows manages to do this, employing temporary variables to hold the intermediate results:
T1 = D / E
T2 = C * T1
T3 = -B
A = T3 + T2
A workable intermediate language would, of course, need some other features, like pointers. We’re going to suggest that we create our own intermediate language to investigate how optimizations work. To begin, we need to establish a few rules:
- Instructions consist of one opcode, two operands, and a result. Depending on the instruction, the operands may be empty.
- Assignments are of the form
X := Y op Z, meaningXgets the result ofopapplied toYandZ. - All memory references are explicit load from or store to “temporaries”
tn. - Logical values used in branches are calculated separately from the actual branch.
- Jumps go to absolute addresses.
If we were building a compiler, we’d need to be a little more specific. For our purposes, this will do. Consider the following bit of C code:
while (j < n) {
k = k + j * 2;
m = j * 2;
j++;
}
This loop translates into the intermediate language representation shown here:
A:: t1 := j
t2 := n
t3 := t1 < t2
jmp (B) t3
jmp (C) TRUE
B:: t4 := k
t5 := j
t6 := t5 * 2
t7 := t4 + t6
k := t7
t8 := j
t9 := t8 * 2
m := t9
t10 := j
t11 := t10 + 1
j := t11
jmp (A) TRUE
C::
Each C source line is represented by several IL statements. On many RISC processors, our IL code is so close to machine language that we could turn it directly into object code.6 Often the lowest optimization level does a literal translation from the intermediate language to machine code. When this is done, the code generally is very large and performs very poorly. Looking at it, you can see places to save a few instructions. For instance, j gets loaded into temporaries in four places; surely we can reduce that. We have to do some analysis and make some optimizations.
Basic Blocks
After generating our intermediate language, we want to cut it into basic blocks. These are code sequences that start with an instruction that either follows a branch or is itself a target for a branch. Put another way, each basic block has one entrance (at the top) and one exit (at the bottom). [Figure 2] represents our IL code as a group of three basic blocks. Basic blocks make code easier to analyze. By restricting flow of control within a basic block from top to bottom and eliminating all the branches, we can be sure that if the first statement gets executed, the second one does too, and so on. Of course, the branches haven’t disappeared, but we have forced them outside the blocks in the form of the connecting arrows — the flow graph.
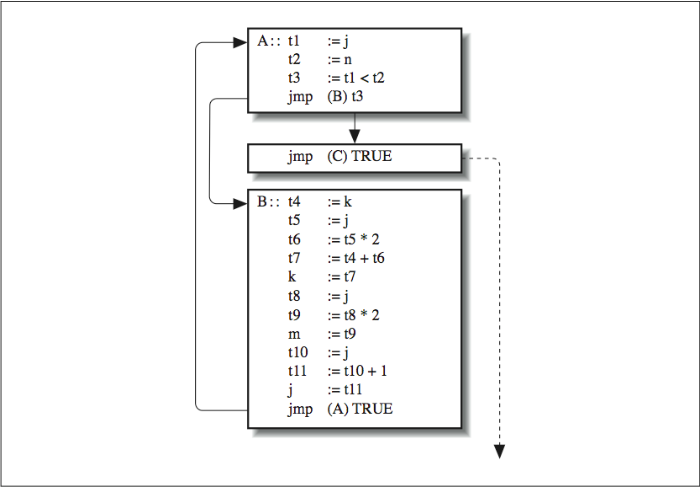
We are now free to extract information from the blocks themselves. For instance, we can say with certainty which variables a given block uses and which variables it defines (sets the value of ). We might not be able to do that if the block contained a branch. We can also gather the same kind of information about the calculations it performs. After we have analyzed the blocks so that we know what goes in and what comes out, we can modify them to improve performance and just worry about the interaction between blocks.
Optimization Levels
There are a wide variety of optimization techniques, and they are not all applicable in all situations. So the user is typically given some choices as to whether or not particular optimizations are performed. Often this is expressed in the form of an optimization level that is specified on the compiler as a command-line option such as –O3.
The different levels of optimization controlled by a compiler flag may include the following:
- No optimization: Generates machine code directly from the intermediate language, which can be very large and slow code. The primary uses of no optimization are for debuggers and establishing the correct program output. Because every operation is done precisely as the user specified, it must be right.
- Basic optimizations:Similar to those described in this chapter. They generally work to minimize the intermediate language and generate fast compact code.
- Interprocedural analysis: Looks beyond the boundaries of a single routine for optimization opportunities. This optimization level might include extending a basic optimization such as copy propagation across multiple routines. Another result of this technique is procedure inlining where it will improve performance.
- Runtime profile analysis: It is possible to use runtime profiles to help the compiler generate improved code based on its knowledge of the patterns of runtime execution gathered from profile information.
- Floating-point optimizations: The IEEE floating-point standard (IEEE 754) specifies precisely how floating- point operations are performed and the precise side effects of these operations. The compiler may identify certain algebraic transformations that increase the speed of the program (such as replacing a division with a reciprocal and a multiplication) but might change the output results from the unoptimized code.
- Data flow analysis: Identifies potential parallelism between instructions, blocks, or even successive loop iterations.
- Advanced optimization: May include automatic vectorization, parallelization, or data decomposition on advanced architecture computers.
These optimizations might be controlled by several different compiler options. It often takes some time to figure out the best combination of compiler flags for a particular code or set of codes. In some cases, programmers compile different routines using different optimization settings for best overall performance.
Classical Optimizations
Once the intermediate language is broken into basic blocks, there are a number of optimizations that can be performed on the code in these blocks. Some optimizations are very simple and affect a few tuples within a basic block. Other optimizations move code from one basic block to another without altering the program results. For example, it is often valuable to move a computation from the body of a loop to the code immediately preceding the loop.
In this section, we are going to list classical optimizations by name and tell you what they are for. We’re not suggesting that you make the changes; most compilers since the mid-1980s automatically perform these optimizations at all but their lowest optimization level. As we said at the start of the chapter, if you understand what the compiler can (and can’t) do, you will become a better programmer because you will be able to play to the compiler’s strengths.
Copy Propagation
To start, let’s look at a technique for untangling calculations. Take a look at the following segment of code: notice the two computations involving X.
X = Y
Z = 1.0 + X
As written, the second statement requires the results of the first before it can proceed — you need X to calculate Z. Unnecessary dependencies could translate into a delay at runtime.7 With a little bit of rearrangement we can make the second statement independent of the first, by propagating a copy of Y. The new calculation for Z uses the value of Y directly:
X = Y
Z = 1.0 + Y
Notice that we left the first statement, X=Y, intact. You may ask, “Why keep it?” The problem is that we can’t tell whether the value of X is needed elsewhere. That is something for another analysis to decide. If it turns out that no other statement needs the new value of X, the assignment is eliminated later by dead code removal.
Constant Folding
A clever compiler can find constants throughout your program. Some of these are “obvious” constants like those defined in parameter statements. Others are less obvious, such as local variables that are never redefined. When you combine them in a calculation, you get a constant expression. The little program below has two constants, I and K:
PROGRAM MAIN
INTEGER I,K
PARAMETER (I = 100)
K = 200
J = I + K
END
Because I and K are constant individually, the combination I+K is constant, which means that J is a constant too. The compiler reduces constant expressions like I+K into constants with a technique called constant folding.
How does constant folding work? You can see that it is possible to examine every path along which a given variable could be defined en route to a particular basic block. If you discover that all paths lead back to the same value, that is a constant; you can replace all references to that variable with that constant. This replacement has a ripple-through effect. If the compiler finds itself looking at an expression that is made up solely of constants, it can evaluate the expression at compile time and replace it with a constant. After several iterations, the compiler will have located most of the expressions that are candidates for constant folding.
A programmer can sometimes improve performance by making the compiler aware of the constant values in your application. For example, in the following code segment:
X = X * Y
the compiler may generate quite different runtime code if it knew that Y was 0, 1, 2, or 175.32. If it does not know the value for Y, it must generate the most conservative (not necessarily the fastest) code sequence. A programmer can communicate these values through the use of the PARAMETER statement in FORTRAN. By the use of a parameter statement, the compiler knows the values for these constants at runtime. Another example we have seen is:
DO I = 1,10000
DO J=1,IDIM
.....
ENDDO
ENDDO
After looking at the code, it’s clear that IDIM was either 1, 2, or 3, depending on the data set in use. Clearly if the compiler knew that IDIM was 1, it could generate much simpler and faster code.
Dead Code Removal
Programs often contain sections of dead code that have no effect on the answers and can be removed. Occasionally, dead code is written into the program by the author, but a more common source is the compiler itself; many optimizations produce dead code that needs to be swept up afterwards.
Dead code comes in two types:
- Instructions that are unreachable
- Instructions that produce results that are never used
You can easily write some unreachable code into a program by directing the flow of control around it — permanently. If the compiler can tell it’s unreachable, it will eliminate it. For example, it’s impossible to reach the statement I = 4 in this program:
PROGRAM MAIN
I = 2
WRITE (*,*) I
STOP
I = 4
WRITE (*,*) I
END
The compiler throws out everything after the STOP statement and probably gives you a warning. Unreachable code produced by the compiler during optimization will be quietly whisked away.
Computations with local variables can produce results that are never used. By analyzing a variable’s definitions and uses, the compiler can see whether any other part of the routine references it. Of course the compiler can’t tell the ultimate fate of variables that are passed between routines, external or common, so those computations are always kept (as long as they are reachable).8 In the following program, computations involving k contribute nothing to the final answer and are good candidates for dead code elimination:
main ()
{
int i,k;
i = k = 1;
i += 1;
k += 2;
printf ("%d\n",i);
}
Dead code elimination has often produced some amazing benchmark results from poorly written benchmarks. See [Section 2.1.6] for an example of this type of code.
Strength Reduction
Operations or expressions have time costs associated with them. Sometimes it’s possible to replace a more expensive calculation with a cheaper one. We call this strength reduction. The following code fragment contains two expensive operations:
REAL X,Y
Y = X**2
J = K*2
For the exponentiation operation on the first line, the compiler generally makes an embedded mathematical subroutine library call. In the library routine, X is converted to a logarithm, multiplied, then converted back. Overall, raising X to a power is expensive — taking perhaps hundreds of machine cycles. The key is to notice that X is being raised to a small integer power. A much cheaper alternative would be to express it as X*X, and pay only the cost of multiplication. The second statement shows integer multiplication of a variable K by 2. Adding K+K yields the same answer, but takes less time.
There are many opportunities for compiler-generated strength reductions; these are just a couple of them. We will see an important special case when we look at induction variable simplification. Another example of a strength reduction is replacing multiplications by integer powers of two by logical shifts.
Variable Renaming
In [Section 5.1.1], we talked about register renaming. Some processors can make runtime decisions to replace all references to register 1 with register 2, for instance, to eliminate bottlenecks. Register renaming keeps instructions that are recycling the same registers for different purposes from having to wait until previous instructions have finished with them.
The same situation can occur in programs — the same variable (i.e., memory location) can be recycled for two unrelated purposes. For example, see the variable x in the following fragment:
x = y * z;
q = r + x + x;
x = a + b;
When the compiler recognizes that a variable is being recycled, and that its current and former uses are independent, it can substitute a new variable to keep the calculations separate:
x0 = y * z;
q = r + x0 + x0;
x = a + b;
Variable renaming is an important technique because it clarifies that calculations are independent of each other, which increases the number of things that can be done in parallel.
Common Subexpression Elimination
Subexpressions are pieces of expressions. For instance, A+B is a subexpression of C*(A+B). If A+B appears in several places, like it does below, we call it a common subexpression:
D = C * (A + B)
E = (A + B)/2.
Rather than calculate A + B twice, the compiler can generate a temporary variable and use it wherever A + B is required:
temp = A + B
D = C * temp
E = temp/2.
Different compilers go to different lengths to find common subexpressions. Most pairs, such as A+B, are recognized. Some can recognize reuse of intrinsics, such as SIN(X). Don’t expect the compiler to go too far though. Subexpressions like A+B+C are not computationally equivalent to reassociated forms like B+C+A, even though they are algebraically the same. In order to provide predictable results on computations, FORTRAN must either perform operations in the order specified by the user or reorder them in a way to guarantee exactly the same result. Sometimes the user doesn’t care which way A+B+C associates, but the compiler cannot assume the user does not care.
Address calculations provide a particularly rich opportunity for common subexpression elimination. You don’t see the calculations in the source code; they’re generated by the compiler. For instance, a reference to an array element A(I,J) may translate into an intermediate language expression such as:
address(A) + (I-1)*sizeof_datatype(A)
+ (J-1)*sizeof_datatype(A) * column_dimension(A)
If A(I,J) is used more than once, we have multiple copies of the same address computation. Common subexpression elimination will (hopefully) discover the redundant computations and group them together.
Loop-Invariant Code Motion
Loops are where many high performance computing programs spend a majority of their time. The compiler looks for every opportunity to move calculations out of a loop body and into the surrounding code. Expressions that don’t change after the loop is entered (loop-invariant expressions) are prime targets. The following loop has two loop-invariant expressions:
DO I=1,N
A(I) = B(I) + C * D
E = G(K)
ENDDO
Below, we have modified the expressions to show how they can be moved to the outside:
temp = C * D
DO I=1,N
A(I) = B(I) + temp
ENDDO
E = G(K)
It is possible to move code before or after the loop body. As with common subexpression elimination, address arithmetic is a particularly important target for loop- invariant code motion. Slowly changing portions of index calculations can be pushed into the suburbs, to be executed only when needed.
Induction Variable Simplification
Loops can contain what are called induction variables. Their value changes as a linear function of the loop iteration count. For example, K is an induction variable in the following loop. Its value is tied to the loop index:
DO I=1,N
K = I*4 + M
...
ENDDO
Induction variable simplification replaces calculations for variables like K with simpler ones. Given a starting point and the expression’s first derivative, you can arrive at K’s value for the nth iteration by stepping through the n-1 intervening iterations:
K = M
DO I=1,N
K = K + 4
...
ENDDO
The two forms of the loop aren’t equivalent; the second won’t give you the value of K given any value of I. Because you can’t jump into the middle of the loop on the nth iteration, K always takes on the same values it would have if we had kept the original expression.
Induction variable simplification probably wouldn’t be a very important optimization, except that array address calculations look very much like the calculation for K in the example above. For instance, the address calculation for A(I) within a loop iterating on the variable I looks like this:
address = base_address(A) + (I-1) * sizeof_datatype(A)
Performing all that math is unnecessary. The compiler can create a new induction variable for references to A and simplify the address calculations:
outside the loop...
address = base_address(A) - (1 * sizeof_datatype(A))
indie the loop...
address = address + sizeof_datatype(A)
Induction variable simplification is especially useful on processors that can automatically increment a register each time it is used as a pointer for a memory reference. While stepping through a loop, the memory reference and the address arithmetic can both be squeezed into a single instruction—a great savings.
Object Code Generation
Precompilation, lexical analysis, parsing, and many optimization techniques are somewhat portable, but code generation is very specific to the target processor. In some ways this phase is where compilers earn their keep on single-processor RISC systems.
Anything that isn’t handled in hardware has to be addressed in software. That means if the processor can’t resolve resource conflicts, such as overuse of a register or pipeline, then the compiler is going to have to take care of it. Allowing the compiler to take care of it isn’t necessarily a bad thing — it’s a design decision. A complicated compiler and simple, fast hardware might be cost effective for certain applications. Two processors at opposite ends of this spectrum are the MIPS R2000 and the HP PA-8000. The first depends heavily on the compiler to schedule instructions and fairly distribute resources. The second manages both things at runtime, though both depend on the compiler to provide a balanced instruction mix.
In all computers, register selection is a challenge because, in spite of their numbers, registers are precious. You want to be sure that the most active variables become register resident at the expense of others. On machines without register renaming (see [Section 5.1.1]), you have to be sure that the compiler doesn’t try to recycle registers too quickly, otherwise the processor has to delay computations as it waits for one to be freed.
Some instructions in the repertoire also save your compiler from having to issue others. Examples are auto-increment for registers being used as array indices or conditional assignments in lieu of branches. These both save the processor from extra calculations and make the instruction stream more compact.
Lastly, there are opportunities for increased parallelism. Programmers generally think serially, specifying steps in logical succession. Unfortunately, serial source code makes serial object code. A compiler that hopes to efficiently use the parallelism of the processor will have to be able to move instructions around and find operations that can be issued side by side. This is one of the biggest challenges for compiler writers today. As superscalar and very long instruction word (VLIW) designs become capable of executing more instructions per clock cycle, the compiler will have to dig deeper for operations that can execute at the same time.
Closing Notes
This chapter has been a basic introduction into how an optimizing compiler operates. However, this is not the last we will talk about compilers. In order to perform the automatic vectorization, parallelization, and data decomposition, compilers must further analyze the source code. As we encounter these topics, we will discuss the compiler impacts and how programmers can best interact with compilers.
For single-processor modern RISC architectures, compilers usually generate better code than most assembly language programmers. Instead of compensating for a simplistic compiler by adding hand optimizations, we as programmers must keep our programs simple so as not to confuse the compiler. By understanding the patterns that compilers are quite capable of optimizing, we can focus on writing straightforward programs that are portable and understandable.
Exercises
Exercise \(\PageIndex{1}\)
Does your compiler recognize dead code in the program below? How can you be sure? Does the compiler give you a warning?
main()
{
int k=1;
if (k == 0)
printf ("This statement is never executed.\n");
}
Exercise \(\PageIndex{2}\)
Compile the following code and execute it under various optimization levels.
Try to guess the different types of optimizations that are being performed to improve the performance as the optimization is increased.
REAL*8 A(1000000)
DO I=1,1000000
A(I) = 3.1415927
ENDDO
DO I=1,1000000
A(I) = A(I) * SIN(A(I)) + COS(A(I)) ENDDO
PRINT *,"All Done"
Exercise \(\PageIndex{3}\)
Take the following code segment and compile it at various optimization levels. Look at the generated assembly language code (–S option on some compilers) and find the effects of each optimization level on the machine language. Time the program to see the performance at the different optimization levels. If you have access to multiple architectures, look at the code generated using the same optimization levels on different architectures.
REAL*8 A(1000000)
COMMON/BLK/A
.... Call Time
DO I=1,1000000
A(I) = A(I) + 1.234
ENDDO
.... Call Time
END
Why is it necessary to put the array into a common block?
Footnotes
- However, you can sometimes trade accuracy for speed.
- The Livermore Loops was a benchmark that specifically tested the capability of a compiler to effectively optimize a set of loops. In addition to being a performance benchmark, it was also a compiler benchmark.
- Just for the record, both the authors of this book are quite accomplished in C, C++, and FORTRAN, so they have no preconceived notions.
- By “definitions,” we mean the assignment of values: not declarations.
- More generally, code can be cast as n-tuples. It depends on the level of the intermediate language.
- See [Section 5.2.1] for some examples of machine code translated directly from intermediate language.
- This code is an example of a flow dependence. I describe dependencies in detail in [Section 3.1.1].
- If a compiler does sufficient interprocedural analysis, it can even optimize variables across routine boundaries. Interprocedural analysis can be the bane of benchmark codes trying to time a computation without using the results of the computation.


