5.1: Language Support for Performance
- Page ID
- 13442
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
This chapter discusses the programming languages that are used on the largest parallel processing systems. Usually when you are faced with porting and tuning your code on a new scalable architecture architecture, you have to sit back and think about your application for a moment. Sometimes fundamental changes to your algorithm are needed before you can begin to work on the new architecture. Don't be surprised if you need to rewrite all or portions of the application in one of these languages. Modifications on one system may not give a performance benefit on another system. But if the application is important enough, it's worth the effort to improve its performance.
In this chapter, we cover:
- FORTRAN 90
- HPF: High Performance FORTRAN
These languages are designed for use on high-end computing systems. We will follow a simple program through each of these languages, using a simple finite-difference computation that roughly models heat flow. It's a classic problem that contains a great deal of parallelism and is easily solved on a wide variety of parallel architectures.
We introduce and discuss the concept of single program multiple data (SPMD) in that we treat MIMD computers as SIMD computers. We write our applications as if a large SIMD system were going to solve the problem. Instead of actually using a SIMD system, the resulting application is compiled for a MIMD system. The implicit synchronization of the SIMD systems is replaced by explicit synchronization at runtime on the MIMD systems.
Data-Parallel Problem: Heat Flow
A classic problem that explores scalable parallel processing is the heat flow problem. The physics behind this problem lie in partial differential equations.
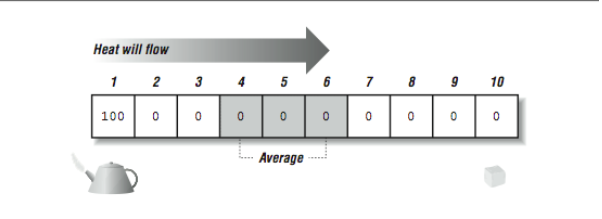
We will start with a one-dimensional metal plate (also known as a rod), and move to a two-dimensional plate in later examples. We start with a rod that is at zero degrees celsius. Then we place one end in 100 degree steam and the other end in zero degree ice. We want to simulate how the heat flows from one end to another. And the resulting temperatures along points on the metal rod after the temperature has stabilized.
To do this we break the rod into 10 segments and track the temperature over time for each segment. Intuitively, within a time step, the next temperature of a portion of the plate is an average of the surrounding temperatures. Given fixed temperatures at some points in the rod, the temperatures eventually converge to a steady state after sufficient time steps. [Figure 1] shows the setup at the beginning of the simulation.
A simplistic implementation of this is as follows:
PROGRAM HEATROD
PARAMETER(MAXTIME=200)
INTEGER TICKS,I,MAXTIME
REAL*4 ROD(10)
ROD(1) = 100.0
DO I=2,9
ROD(I) = 0.0
ENDDO
ROD(10) = 0.0
DO TICKS=1,MAXTIME
IF ( MOD(TICKS,20) .EQ. 1 ) PRINT 100,TICKS,(ROD(I),I=1,10)
DO I=2,9
ROD(I) = (ROD(I-1) + ROD(I+1) ) / 2
ENDDO
ENDDO
100 FORMAT(I4,10F7.2)
END
The output of this program is as follows:
% f77 heatrod.f heatrod.f: MAIN heatrod: % a.out 1 100.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 21 100.00 87.04 74.52 62.54 51.15 40.30 29.91 19.83 9.92 0.00 41 100.00 88.74 77.51 66.32 55.19 44.10 33.05 22.02 11.01 0.00 61 100.00 88.88 77.76 66.64 55.53 44.42 33.31 22.21 11.10 0.00 81 100.00 88.89 77.78 66.66 55.55 44.44 33.33 22.22 11.11 0.00 101 100.00 88.89 77.78 66.67 55.56 44.44 33.33 22.22 11.11 0.00 121 100.00 88.89 77.78 66.67 55.56 44.44 33.33 22.22 11.11 0.00 141 100.00 88.89 77.78 66.67 55.56 44.44 33.33 22.22 11.11 0.00 161 100.00 88.89 77.78 66.67 55.56 44.44 33.33 22.22 11.11 0.00 181 100.00 88.89 77.78 66.67 55.56 44.44 33.33 22.22 11.11 0.00 %
Clearly, by Time step 101, the simulation has converged to two decimal places of accuracy as the numbers have stopped changing. This should be the steady-state approximation of the temperature at the center of each segment of the bar.
Now, at this point, astute readers are saying to themselves, "Um, don't look now, but that loop has a flow dependency." You would also claim that this won't even parallelize a little bit. It is so bad you can't even unroll the loop for a little instruction-level parallelism!
A person familiar with the theory of heat flow will also point out that the above loop doesn't exactly implement the heat flow model. The problem is that the values on the right side of the assignment in the ROD loop are supposed to be from the previous time step, and that the value on the left side is the next time step. Because of the way the loop is written, the ROD(I-1) value is from the next time step, as shown in this section.
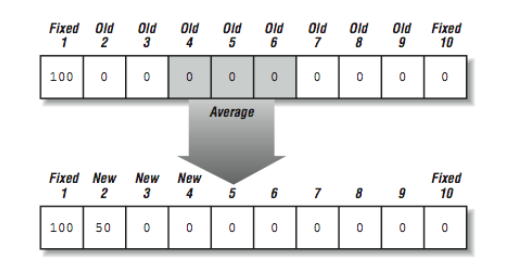
This can be solved using a technique called red-black, where we alternate between two arrays. [Figure 3] shows how the red-black version of the computation operates. This kills two birds with one stone! Now the mathematics is precisely correct, and there is no recurrence. Sounds like a real win-win situation.

The only downside to this approach is that it takes twice the memory storage and twice the memory bandwidth.1 The modified code is as follows:
PROGRAM HEATRED
PARAMETER(MAXTIME=200)
INTEGER TICKS,I,MAXTIME
REAL*4 RED(10),BLACK(10)
RED(1) = 100.0
BLACK(1) = 100.0
DO I=2,9
RED(I) = 0.0
ENDDO
RED(10) = 0.0
BLACK(10) = 0.0
DO TICKS=1,MAXTIME,2
IF ( MOD(TICKS,20) .EQ. 1 ) PRINT 100,TICKS,(RED(I),I=1,10)
DO I=2,9
BLACK(I) = (RED(I-1) + RED(I+1) ) / 2
ENDDO
DO I=2,9
RED(I) = (BLACK(I-1) + BLACK(I+1) ) / 2
ENDDO
ENDDO
100 FORMAT(I4,10F7.2)
END
The output for the modified program is:
% f77 heatred.f heatred.f: MAIN heatred: % a.out 1 100.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 21 100.00 82.38 66.34 50.30 38.18 26.06 18.20 10.35 5.18 0.00 41 100.00 87.04 74.52 61.99 50.56 39.13 28.94 18.75 9.38 0.00 61 100.00 88.36 76.84 65.32 54.12 42.91 32.07 21.22 10.61 0.00 81 100.00 88.74 77.51 66.28 55.14 44.00 32.97 21.93 10.97 0.00 101 100.00 88.84 77.70 66.55 55.44 44.32 33.23 22.14 11.07 0.00 121 100.00 88.88 77.76 66.63 55.52 44.41 33.30 22.20 11.10 0.00 141 100.00 88.89 77.77 66.66 55.55 44.43 33.32 22.22 11.11 0.00 161 100.00 88.89 77.78 66.66 55.55 44.44 33.33 22.22 11.11 0.00 181 100.00 88.89 77.78 66.67 55.55 44.44 33.33 22.22 11.11 0.00 %
Interestingly, the modified program takes longer to converge than the first version. It converges at Time step 181 rather than 101. If you look at the first version, because of the recurrence, the heat ended up flowing up faster from left to right because the left element of each average was the next-time-step value. It may seem nifty, but it's wrong.2 Generally, in this problem, either approach converges to the same eventual values within the limits of floating-point representation.
This heat flow problem is extremely simple, and in its red-black form, it's inherently very parallel with very simple data interactions. It's a good model for a wide range of problems where we are discretizing two-dimensional or three-dimensional space and performing some simple simulations in that space.
This problem can usually be scaled up by making a finer grid. Often, the benefit of scalable processors is to allow a finer grid rather than a faster time to solution. For example, you might be able to to a worldwide weather simulation using a 200-mile grid in four hours on one processor. Using 100 processors, you may be able to do the simulation using a 20-mile grid in four hours with much more accurate results. Or, using 400 processors, you can do the finer grid simulation in one hour.
Explicity Parallel Languages
As we've seen throughout this book, one of biggest tuning challenges is getting the compiler to recognize that a particular code segment can be parallelized. This is particularly true for numerical codes, where the potential payback is greatest. Think about this: if you know that something is parallel, why should there be any difficulty getting the compiler to recognize it? Why can't you just write it down, and have the compiler say "Yes, this is to be done in parallel."
The problem is that the most commonly used languages don't offer any constructs for expressing parallel computations. You are forced to express yourself in primitive terms, as if you were a caveman with a grand thought but no vocabulary to voice it. This is particularly true of FORTRAN and C. They do not support a notion of parallel computations, which means that programmers must reduce calculations to sequential steps. That sounds cumbersome, but most programmers do it so naturally that they don't even realize how good they are at it.
For example, let's say we want to add two vectors, A and B. How would we do it? We would probably write a little loop without a moment's thought:
DO I=1,N
C(I) = A(I) + B(I)
END DO
This seems reasonable, but look what happened. We imposed an order on the calculations! Wouldn't it be enough to say "C gets A plus B"? That would free the compiler to add the vectors using any hardware at its disposal, using any method it likes. This is what parallel languages are about. They seek to supply primitives suitable for expressing parallel computations.
New parallel languages aren't being proposed as rapidly as they were in the mid-1980s. Developers have realized that you can come up with a wonderful scheme, but if it isn't compatible with FORTRAN or C, few people will care about it. The reason is simple: there are billions of lines of C and FORTRAN code, but only a few lines of Fizgibbet, or whatever it is you call your new parallel language. Because of the predominance of C and FORTRAN, the most significant parallel language activities today seek to extend those languages, thus protecting the 20 or 30 years of investment in programs already written.3 It is too tempting for the developers of a new language to test their language on the eight-queens problem and the game of life, get good results, then declare it ready for prime time and begin waiting for the hordes of programmers converting to their particular language.
FORTRAN 90
The previous American National Standards Institute (ANSI) FORTRAN standard release, FORTRAN 77 (X3.9-1978), was written to promote portability of FORTRAN programs between different platforms. It didn't invent new language components, but instead incorporated good features that were already available in production compilers. Unlike FORTRAN 77, FORTRAN 90 (ANSI X3.198-1992) brings new extensions and features to the language. Some of these just bring FORTRAN up to date with newer languages like C (dynamic memory allocation, scoping rules) and C++ (generic function interfaces). But some of the new features are unique to FORTRAN (array operations). Interestingly, while the FORTRAN 90 specification was being developed, the dominant high performance computer architectures were scalable SIMD systems such as the Connection Machine and shared-memory vector-parallel processor systems from companies like Cray Research.
FORTRAN 90 does a surprisingly good job of meeting the needs of these very different architectures. Its features also map reasonably well onto the new shared uniform memory multiprocessors. However, as we will see later, FORTRAN 90 alone is not yet sufficient to meet the needs of the scalable distributed and nonuniform access memory systems that are becoming dominant at the high end of computing.
The FORTRAN 90 extensions to FORTRAN 77 include:
- Array constructs
- Dynamic memory allocation and automatic variables
- Pointers
- New data types, structures
- New intrinsic functions, including many that operate on vectors or matrices
- New control structures, such as a WHERE statement
- Enhanced procedure interfaces
FORTRAN 90 Array Constructs
With FORTRAN 90 array constructs, you can specify whole arrays or array sections as the participants in unary and binary operations. These constructs are a key feature for "unserializing" applications so that they are better suited to vector computers and parallel processors. For example, say you wish to add two vectors, A and B. In FORTRAN 90, you can express this as a simple addition operation, rather than a traditional loop. That is, you can write:
A = A + B
instead of the traditional FORTRAN 77 loop:
DO I=1,N
A(I) = A(I) + B(I)
ENDDO
The code generated by the compiler on your workstation may not look any different, but for some of the parallel machines available now and workstations just around the corner, the difference are significant. The FORTRAN 90 version states explicitly that the computations can be performed in any order, including all in parallel at the same time.
One important effect of this is that if the FORTRAN 90 version experienced a floating-point fault adding element 17, and you were to look at the memory in a debugger, it would be perfectly legal for element 27 to be already computed.
You are not limited to one-dimensional arrays. For instance, the element-wise addition of two two-dimensional arrays could be stated like this:4
A = A + B
in lieu of:
DO J=1,M
DO I=1,N
A(I,J) = A(I,J) + B(I,J)
END DO
END DO
Naturally, when you want to combine two arrays in an operation, their shapes have to be compatible. Adding a seven-element vector to an eight-element vector doesn't make sense. Neither would multiplying a 2×4 array by a 3×4 array. When the two arrays have compatible shapes, relative to the operation being performed upon them, we say they are in shape conformance, as in the following code:
DOUBLE PRECISION A(8), B(8)
...
A = A + B
Scalars are always considered to be in shape conformance with arrays (and other scalars). In a binary operation with an array, a scalar is treated as an array of the same size with a single element duplicated throughout.
Still, we are limited. When you reference a particular array, A, for example, you reference the whole thing, from the first element to the last. You can imagine cases where you might be interested in specifying a subset of an array. This could be either a group of consecutive elements or something like "every eighth element" (i.e., a non-unit stride through the array). Parts of arrays, possibly noncontiguous, are called array sections.
FORTRAN 90 array sections can be specified by replacing traditional subscripts with triplets of the form a:b:c, meaning "elements a through b, taken with an increment of c." You can omit parts of the triplet, provided the meaning remains clear. For example, a:b means "elements a through b;" a: means "elements from a to the upper bound with an increment of 1." Remember that a triplet replaces a single subscript, so an n-dimension array can have n triplets.
You can use triplets in expressions, again making sure that the parts of the expression are in conformance. Consider these statements:
REAL X(10,10), Y(100)
...
X(10,1:10) = Y(91:100)
X(10,:) = Y(91:100)
The first statement above assigns the last 10 elements of Y to the 10th row of X. The second statement expresses the same thing slightly differently. The lone " : " tells the compiler that the whole range (1 through 10) is implied.
FORTRAN 90 Intrinsics
FORTRAN 90 extends the functionality of FORTRAN 77 intrinsics, and adds many new ones as well, including some intrinsic subroutines. Most can be array-valued: they can return arrays sections or scalars, depending on how they are invoked. For example, here's a new, array-valued use of the SIN intrinsic:
REAL A(100,10,2)
...
A = SIN(A)
Each element of array A is replaced with its sine. FORTRAN 90 intrinsics work with array sections too, as long as the variable receiving the result is in shape conformance with the one passed:
REAL A(100,10,2)
REAL B(10,10,100)
...
B(:,:,1) = COS(A(1:100:10,:,1))
Other intrinsics, such as SQRT, LOG, etc., have been extended as well. Among the new intrinsics are:
- Reductions: FORTRAN 90 has vector reductions such as
MAXVAL,MINVAL, andSUM. For higher-order arrays (anything more than a vector) these functions can perform a reduction along a particular dimension. Additionally, there is aDOT_PRODUCTfunction for the vectors. - Matrix multiplication: Intrinsics
MATMULandTRANSPOSEcan manipulate whole matrices. - Constructing or reshaping arrays:
RESHAPEallows you to create a new array from elements of an old one with a different shape.SPREADreplicates an array along a new dimension.MERGEcopies portions of one array into another under control of a mask.CSHIFTallows an array to be shifted in one or more dimensions. - Inquiry functions:
SHAPE,SIZE,LBOUND, andUBOUNDlet you ask questions about how an array is constructed. - Parallel tests: Two other new reduction intrinsics,
ANYandALL, are for testing many array elements in parallel.
New Control Features
FORTRAN 90 includes some new control features, including a conditional assignment primitive called WHERE, that puts shape-conforming array assignments under control of a mask as in the following example. Here's an example of the WHERE primitive:
REAL A(2,2), B(2,2), C(2,2)
DATA B/1,2,3,4/, C/1,1,5,5/
...
WHERE (B .EQ. C)
A = 1.0
C = B + 1.0
ELSEWHERE
A = -1.0
ENDWHERE
In places where the logical expression is TRUE, A gets 1.0 and C gets B+1.0. In the ELSEWHERE clause, A gets -1.0. The result of the operation above would be arrays A and C with the elements:
A = 1.0 -1.0 C = 2.0 5.0
-1.0 -1.0 1.0 5.0
Again, no order is implied in these conditional assignments, meaning they can be done in parallel. This lack of implied order is critical to allowing SIMD computer systems and SPMD environments to have flexibility in performing these computations.
Automatic and Allocatable Arrays
Every program needs temporary variables or work space. In the past, FORTRAN programmers have often managed their own scratch space by declaring an array large enough to handle any temporary requirements. This practice gobbles up memory (albeit virtual memory, usually), and can even have an effect on performance. With the ability to allocate memory dynamically, programmers can wait until later to decide how much scratch space to set aside. FORTRAN 90 supports dynamic memory allocation with two new language features: automatic arrays and allocatable arrays.
Like the local variables of a C program, FORTRAN 90's automatic arrays are assigned storage only for the life of the subroutine or function that contains them. This is different from traditional local storage for FORTRAN arrays, where some space was set aside at compile or link time. The size and shape of automatic arrays can be sculpted from a combination of constants and arguments. For instance, here's a declaration of an automatic array, B, using FORTRAN 90's new specification syntax:
SUBROUTINE RELAX(N,A)
INTEGER N
REAL, DIMENSION (N) :: A, B
Two arrays are declared: A, the dummy argument, and B, an automatic, explicit shape array. When the subroutine returns, B ceases to exist. Notice that the size of B is taken from one of the arguments, N.
Allocatable arrays give you the ability to choose the size of an array after examining other variables in the program. For example, you might want to determine the amount of input data before allocating the arrays. This little program asks the user for the matrix's size before allocating storage:
INTEGER M,N
REAL, ALLOCATABLE, DIMENSION (:,:) :: X
...
WRITE (*,*) 'ENTER THE DIMENSIONS OF X'
READ (*,*) M,N
ALLOCATE (X(M,N))
...
do something with X
...
DEALLOCATE (X)
...
The ALLOCATE statement creates an M × N array that is later freed by the DEALLOCATE statement. As with C programs, it's important to give back allocated memory when you are done with it; otherwise, your program might consume all the virtual storage available.
Heat Flow in FORTRAN 90
The heat flow problem is an ideal program to use to demonstrate how nicely FORTRAN 90 can express regular array programs:
PROGRAM HEATROD
PARAMETER(MAXTIME=200)
INTEGER TICKS,I,MAXTIME
REAL*4 ROD(10)
ROD(1) = 100.0
DO I=2,9
ROD(I) = 0.0
ENDDO
ROD(10) = 0.0
DO TICKS=1,MAXTIME
IF ( MOD(TICKS,20) .EQ. 1 ) PRINT 100,TICKS,(ROD(I),I=1,10)
ROD(2:9) = (ROD(1:8) + ROD(3:10) ) / 2
ENDDO
100 FORMAT(I4,10F7.2)
END
The program is identical, except the inner loop is now replaced by a single statement that computes the "new" section by averaging a strip of the "left" elements and a strip of the "right" elements.
The output of this program is as follows:
E6000: f90 heat90.f E6000:a.out 1 100.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 21 100.00 82.38 66.34 50.30 38.18 26.06 18.20 10.35 5.18 0.00 41 100.00 87.04 74.52 61.99 50.56 39.13 28.94 18.75 9.38 0.00 61 100.00 88.36 76.84 65.32 54.12 42.91 32.07 21.22 10.61 0.00 81 100.00 88.74 77.51 66.28 55.14 44.00 32.97 21.93 10.97 0.00 101 100.00 88.84 77.70 66.55 55.44 44.32 33.23 22.14 11.07 0.00 121 100.00 88.88 77.76 66.63 55.52 44.41 33.30 22.20 11.10 0.00 141 100.00 88.89 77.77 66.66 55.55 44.43 33.32 22.22 11.11 0.00 161 100.00 88.89 77.78 66.66 55.55 44.44 33.33 22.22 11.11 0.00 181 100.00 88.89 77.78 66.67 55.55 44.44 33.33 22.22 11.11 0.00 E6000:
If you look closely, this output is the same as the red-black implementation. That is because in FORTRAN 90:
ROD(2:9) = (ROD(1:8) + ROD(3:10) ) / 2
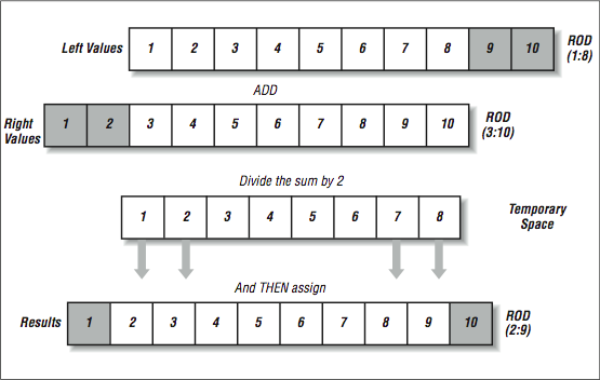
is a single assignment statement. As shown in [Figure 4], the right side is completely evaluated before the resulting array section is assigned into ROD(2:9). For a moment, that might seem unnatural, but consider the following statement:
I = I + 1
We know that if I starts with 5, it's incremented up to six by this statement. That happens because the right side (5+1) is evaluated before the assignment of 6 into I is performed. In FORTRAN 90, a variable can be an entire array. So, this is a red-black operation. There is an "old" ROD on the right side and a "new" ROD on the left side!
To really "think" FORTRAN 90, it's good to pretend you are on an SIMD system with millions of little CPUs. First we carefully align the data, sliding it around, and then— wham— in a single instruction, we add all the aligned values in an instant. [Figure 4] shows graphically this act of "aligning" the values and then adding them. The data flow graph is extremely simple. The top two rows are read-only, and the data flows from top to bottom. Using the temporary space eliminates the seeming dependency. This approach of "thinking SIMD" is one of the ways to force ourselves to focus our thoughts on the data rather than the control. SIMD may not be a good architecture for your problem but if you can express it so that SIMD could work, a good SPMD environment can take advantage of the data parallelism that you have identified.
The above example actually highlights one of the challenges in producing an efficient implementation of FORTRAN 90. If these arrays contained 10 million elements, and the compiler used a simple approach, it would need 30 million elements for the old "left" values, the old "right" values, and for the new values. Data flow optimization is needed to determine just how much extra data must be maintained to give the proper results. If the compiler is clever, the extra memory can be quite small:
SAVE1 = ROD(1)
DO I=2,9
SAVE2 = ROD(I)
ROD(I) = (SAVE1 + ROD(I+1) ) / 2
SAVE1 = SAVE2
ENDDO
This does not have the parallelism that the full red-black implementation has, but it does produce the correct results with only two extra data elements. The trick is to save the old "left" value just before you wipe it out. A good FORTRAN 90 compiler uses data flow analysis, looking at a template of how the computation moves across the data to see if it can save a few elements for a short period of time to alleviate the need for a complete extra copy of the data.
The advantage of the FORTRAN 90 language is that it's up to the compiler whether it uses a complete copy of the array or a few data elements to insure that the program executes properly. Most importantly, it can change its approach as you move from one architecture to another.
FORTRAN 90 Versus FORTRAN 77
Interestingly, FORTRAN 90 has never been fully embraced by the high performance community. There are a few reasons why:
- There is a concern that the use of pointers and dynamic data structures would ruin performance and lose the optimization advantages of FORTRAN over C. Some people would say that FORTRAN 90 is trying to be a better C than C. Others would say, "who wants to become more like the slower language!" Whatever the reason, there was some controversy when FORTRAN 90 was implemented, leading to some reluctance in adoption by programmers. Some vendors said, "You can use FORTRAN 90, but FORTRAN 77 will always be faster."
- Because vendors often implemented different subsets of FORTRAN 90, it was not as portable as FORTRAN 77. Because of this, users who needed maximum portability stuck with FORTRAN 77.
- Sometimes vendors purchased their fully compliant FORTRAN 90 compilers from a third party who demanded high license fees. So, you could get the free (and faster according to the vendor) FORTRAN 77 or pay for the slower (wink wink) FORTRAN 90 compiler.
- Because of these factors, the number of serious applications developed in FORTRAN 90 was small. So the benchmarks used to purchase new systems were almost exclusively FORTRAN 77. This further motivated the vendors to improve their FORTRAN 77 compilers instead of their FORTRAN 90 compilers.
- As the FORTRAN 77 compilers became more sophisticated using data flow analysis, it became relatively easy to write portable "parallel" code in FORTRAN 77, using the techniques we have discussed in this book.
- One of the greatest potential benefits to FORTRAN 90 was portability between SIMD and the parallel/vector supercomputers. As both of these architectures were replaced with the shared uniform memory multiprocessors, FORTRAN 77 became the language that afforded the maximum portability across the computers typically used by high performance computing programmers.
- The FORTRAN 77 compilers supported directives that allowed programmers to fine-tune the performance of their applications by taking full control of the parallelism. Certain dialects of FORTRAN 77 essentially became parallel programming "assembly language." Even highly tuned versions of these codes were relatively portable across the different vendor shared uniform memory multiprocessors.
So, events conspired against FORTRAN 90 in the short run. However, FORTRAN 77 is not well suited for the distributed memory systems because it does not lend itself well to data layout directives. As we need to partition and distribute the data carefully on these new systems, we must give the compiler lots of flexibility. FORTRAN 90 is the language best suited to this purpose.
FORTRAN 90 Summary
Well, that's the whirlwind tour of FORTRAN 90. We have probably done the language a disservice by covering it so briefly, but we wanted to give you a feel for it. There are many features that were not discussed. If you would like to learn more, we recommend FORTRAN 90 Explained, by Michael Metcalf and John Reid (Oxford University Press).
FORTRAN 90 by itself is not sufficient to give us scalable performance on distributed memory systems. So far, compilers are not yet capable of performing enough data flow analysis to decide where to store the data and when to retrieve the memory. So, for now, we programmers must get involved with the data layout. We must decompose the problem into parallel chunks that can be individually processed. We have several options. We can use High Performance FORTRAN and leave some of the details to the compiler, or we can use explicit message-passing and take care of all of the details ourselves.
Problem Decomposition
There are three main approaches to dividing or decomposing work for distribution among multiple CPUs:
- Decomposing computations: We have already discussed this technique. When the decomposition is done based on computations, we come up with some mechanism to divide the computations (such as the iterations of a loop) evenly among our processors. The location of the data is generally ignored, and the primary issues are iteration duration and uniformity. This is the preferred technique for the shared uniform memory systems because the data can be equally accessed by any processor.
- Decomposing data: When memory access is nonuniform, the tendency is to focus on the distribution of the data rather than computations. The assumption is that retrieving "remote" data is costly and should be minimized. The data is distributed among the memories. The processor that contains the data performs the computations on that data after retrieving any other data necessary to perform the computation.
- Decomposing tasks: When the operations that must be performed are very independent, and take some time, a task decomposition can be performed. In this approach a master process/thread maintains a queue of work units. When a processor has available resources, it retrieves the next "task" from the queue and begins processing. This is a very attractive approach for embarrassingly parallel computations.5
In some sense, the rest of this chapter is primarily about data decomposition. In a distributed memory system, the communication costs usually are the dominant performance factor. If your problem is so embarrassingly parallel that it can be distributed as tasks, then nearly any technique will work. Data-parallel problems occur in many disciplines. They vary from those that are extremely parallel to those that are just sort of parallel. For example, fractal calculations are extremely parallel; each point is derived independently of the rest. It's simple to divide fractal calculations among processors. Because the calculations are independent, the processors don't have to coordinate or share data.
Our heat flow problem when expressed in its red-black (or FORTRAN 90) form is extremely parallel but requires some sharing of data. A gravitational model of a galaxy is another kind of parallel program. Each point exerts an influence on every other. Therefore, unlike the fractal calculations, the processors do have to share data.
In either case, you want to arrange calculations so that processors can say to one another, "you go over there and work on that, and I'll work on this, and we'll get together when we are finished."
Problems that offer less independence between regions are still very good candidates for domain decomposition. Finite difference problems, short-range particle interaction simulations, and columns of matrices can be treated similarly. If you can divide the domain evenly between the processors, they each do approximately the same amount of work on their way to a solution.
Other physical systems are not so regular or involve long-range interactions. The nodes of an unstructured grid may not be allocated in direct correspondence to their physical locations, for instance. Or perhaps the model involves long-range forces, such as particle attractions. These problems, though more difficult, can be structured for parallel machines as well. Sometimes various simplifications, or "lumping" of intermediate effects, are needed. For instance, the influence of a group of distant particles upon another may be treated as if there were one composite particle acting at a distance. This is done to spare the communications that would be required if every processor had to talk to every other regarding each detail. In other cases, the parallel architecture offers opportunities to express a physical system in different and clever ways that make sense in the context of the machine. For instance, each particle could be assigned to its own processor, and these could slide past one another, summing interactions and updating a time step.
Depending on the architecture of the parallel computer and problem, a choice for either dividing or replicating (portions of) the domain may add unacceptable overhead or cost to the whole project.
For a large problem, the dollar value of main memory may make keeping separate local copies of the same data out of the question. In fact, a need for more memory is often what drives people to parallel machines; the problem they need to solve can't fit in the memory of a conventional computer.
By investing some effort, you could allow the domain partitioning to evolve as the program runs, in response to an uneven load distribution. That way, if there were a lot of requests for As, then several processors could dynamically get a copy of the A piece of the domain. Or the A piece could be spread out across several processors, each handling a different subset of the A definitions. You could also migrate unique copies of data from place to place, changing their home as needed.
When the data domain is irregular, or changes over time, the parallel program encounters a load-balancing problem. Such a problem becomes especially apparent when one portion of the parallel computations takes much longer to complete than the others. A real-world example might be an engineering analysis on an adaptive grid. As the program runs, the grid becomes more refined in those areas showing the most activity. If the work isn't reapportioned from time to time, the section of the computer with responsibility for the most highly refined portion of the grid falls farther and farther behind the performance of the rest of the machine.
High Performance FORTRAN (HPF)
In March 1992, the High Performance Fortran Forum (HPFF) began meeting to discuss and define a set of additions to FORTRAN 90 to make it more practical for use in a scalable computing environment. The plan was to develop a specification within the calendar year so that vendors could quickly begin to implement the standard. The scope of the effort included the following:
- Identify scalars and arrays that will be distributed across a parallel machine.
- Say how they will be distributed. Will they be strips, blocks, or something else?
- Specify how these variables will be aligned with respect to one another.
- Redistribute and realign data structures at runtime.
- Add a
FORALLcontrol construct for parallel assignments that are difficult or impossible to construct using FORTRAN 90's array syntax. - Make improvements to the FORTRAN 90
WHEREcontrol construct. - Add intrinsic functions for common parallel operations.
There were several sources of inspiration for the HPF effort. Layout directives were already part of the FORTRAN 90 programming environment for some SIMD computers (i.e., the CM-2). Also, PVM, the first portable message-passing environment, had been released a year earlier, and users had a year of experience trying to decompose by hand programs. They had developed some basic usable techniques for data decomposition that worked very well but required far too much bookkeeping.6
The HPF effort brought together a diverse set of interests from all the major high performance computing vendors. Vendors representing all the major architectures were represented. As a result HPF was designed to be implemented on nearly all types of architectures.
There is an effort underway to produce the next FORTRAN standard: FORTRAN 95. FORTRAN 95 is expected to adopt some but not all of the HPF modifications.
Programming in HPF
At its core, HPF includes FORTRAN 90. If a FORTRAN 90 program were run through an HPF compiler, it must produce the same results as if it were run through a FORTRAN 90 compiler. Assuming an HPF program only uses FORTRAN 90 constructs and HPF directives, a FORTRAN 90 compiler could ignore the directives, and it should produce the same results as an HPF compiler.
As the user adds directives to the program, the semantics of the program are not changed. If the user completely misunderstands the application and inserts extremely ill-conceived directives, the program produces correct results very slowly. An HPF compiler doesn't try to "improve on" the user's directives. It assumes the programmer is omniscient.7
Once the user has determined how the data will be distributed across the processors, the HPF compiler attempts to use the minimum communication necessary and overlaps communication with computation whenever possible. HPF generally uses an "owner computes" rule for the placement of the computations. A particular element in an array is computed on the processor that stores that array element.
All the necessary data to perform the computation is gathered from remote processors, if necessary, to perform the computation. If the programmer is clever in decomposition and alignment, much of the data needed will be from the local memory rather then a remote memory. The HPF compiler is also responsible for allocating any temporary data structures needed to support communications at runtime.
In general, the HPF compiler is not magic - it simply does a very good job with the communication details when the programmer can design a good data decomposition. At the same time, it retains portability with the single CPU and shared uniform memory systems using FORTRAN 90.
HPF data layout directives
Perhaps the most important contributions of HPF are its data layout directives. Using these directives, the programmer can control how data is laid out based on the programmer's knowledge of the data interactions. An example directive is as follows:
REAL*4 ROD(10)
!HPF$ DISTRIBUTE ROD(BLOCK)
The !HPF$ prefix would be a comment to a non-HPF compiler and can safely be ignored by a straight FORTRAN 90 compiler. The DISTRIBUTE directive indicates that the ROD array is to be distributed across multiple processors. If this directive is not used, the ROD array is allocated on one processor and communicated to the other processors as necessary. There are several distributions that can be done in each dimension:
REAL*4 BOB(100,100,100),RICH(100,100,100)
!HPF$ DISTRIBUTE BOB(BLOCK,CYCLIC,*)
!HPF$ DISTRIBUTE RICH(CYCLIC(10))
These distributions operate as follows:
BLOCKThe array is distributed across the processors using contiguous blocks of the index value. The blocks are made as large as possible.CYCLICThe array is distributed across the processors, mapping each successive element to the "next" processor, and when the last processor is reached, allocation starts again on the first processor.CYCLIC(n)The array is distributed the same asCYCLICexcept thatnsuccessive elements are placed on each processor before moving on to the next processor.
Note
All the elements in that dimension are placed on the same processor. This is most useful for multidimensional arrays.
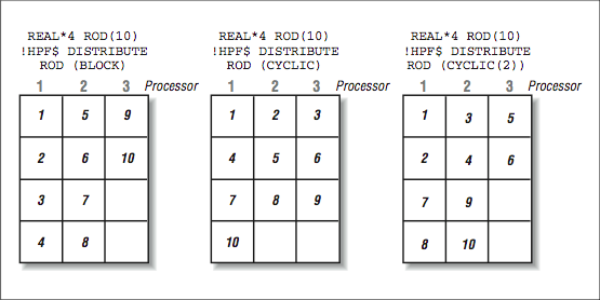
[Figure 5] shows how the elements of a simple array would be mapped onto three processors with different directives.
It must allocate four elements to Processors 1 and 2 because there is no Processor 4 available for the leftover element if it allocated three elements to Processors 1 and 2. In [Figure 5], the elements are allocated on successive processors, wrapping around to Processor 1 after the last processor. In [Figure 5], using a chunk size with CYCLIC is a compromise between pure BLOCK and pure CYCLIC.
To explore the use of the *, we can look at a simple two-dimensional array mapped onto four processors. In [Figure 6], we show the array layout and each cell indicates which processor will hold the data for that cell in the two-dimensional array. In [Figure 6], the directive decomposes in both dimensions simultaneously. This approach results in roughly square patches in the array. However, this may not be the best approach. In the following example, we use the * to indicate that we want all the elements of a particular column to be allocated on the same processor. So, the column values equally distribute the columns across the processors. Then, all the rows in each column follow where the column has been placed. This allows unit stride for the on-processor portions of the computation and is beneficial in some applications. The * syntax is also called on-processor distribution.

When dealing with more than one data structure to perform a computation, you can either separately distribute them or use the ALIGN directive to ensure that corresponding elements of the two data structures are to be allocated together. In the following example, we have a plate array and a scaling factor that must be applied to each column of the plate during the computation:
DIMENSION PLATE(200,200),SCALE(200)
!HPF$ DISTRIBUTE PLATE(*,BLOCK)
!HPF$ ALIGN SCALE(I) WITH PLATE(J,I)
Or:
DIMENSION PLATE(200,200),SCALE(200)
!HPF$ DISTRIBUTE PLATE(*,BLOCK)
!HPF$ ALIGN SCALE(:) WITH PLATE(*,:)
In both examples, the PLATE and the SCALE variables are allocated to the same processors as the corresponding columns of PLATE. The * and : syntax communicate the same information. When * is used, that dimension is collapsed, and it doesn't participate in the distribution. When the : is used, it means that dimension follows the corresponding dimension in the variable that has already been distributed.
You could also specify the layout of the SCALE variable and have the PLATE variable "follow" the layout of the SCALE variable:
DIMENSION PLATE(200,200),SCALE(200)
!HPF$ DISTRIBUTE SCALE(BLOCK)
!HPF$ ALIGN PLATE(J,I) WITH SCALE(I)
You can put simple arithmetic expressions into the ALIGN directive subject to some limitations. Other directives include:
PROCESSORSAllows you to create a shape of the processor configuration that can be used to align other data structures.REDISTRIBUTE and REALIGNAllow you to dynamically reshape data structures at runtime as the communication patterns change during the course of the run.TEMPLATEAllows you to create an array that uses no space. Instead of distributing one data structure and aligning all the other data structures, some users will create and distribute a template and then align all of the real data structures to that template.
The use of directives can range from very simple to very complex. In some situations, you distribute the one large shared structure, align a few related structures and you are done. In other situations, programmers attempt to optimize communications based on the topology of the interconnection network (hypercube, multi-stage interconnection network, mesh, or toroid) using very detailed directives. They also might carefully redistribute the data at the various phases of the computation.
Hopefully your application will yield good performance without too much effort.
HPF control structures
While the HPF designers were in the midst of defining a new language, they set about improving on what they saw as limitations in FORTRAN 90. Interestingly, these modifications are what is being considered as part of the new FORTRAN 95 standard.
The FORALL statement allows the user to express simple iterative operations that apply to the entire array without resorting to a do-loop (remember, do-loops force order). For example:
FORALL (I=1:100, J=1:100) A(I,J) = I + J
This can be expressed in native FORTRAN 90 but it is rather ugly, counterintuitive, and prone to error.
Another control structure is the ability to declare a function as "PURE." A PURE function has no side effects other than through its parameters. The programmer is guaranteeing that a PURE function can execute simultaneously on many processors with no ill effects. This allows HPF to assume that it will only operate on local data and does not need any data communication during the duration of the function execution. The programmer can also declare which parameters of the function are input parameters, output parameters, and input-output parameters.
HPF intrinsics
The companies who marketed SIMD computers needed to come up with significant tools to allow efficient collective operations across all the processors. A perfect example of this is the SUM operation. To SUM the value of an array spread across N processors, the simplistic approach takes N steps. However, it is possible to accomplish it in log(N) steps using a technique called parallel-prefix-sum. By the time HPF was in development, a number of these operations had been identified and implemented. HPF took the opportunity to define standardized syntax for these operations.
A sample of these operations includes:
SUM_PREFIXPerforms various types of parallel-prefix summations.ALL_SCATTERDistributes a single value to a set of processors.GRADE_DOWNSorts into decreasing order.IANYComputes the logical OR of a set of values.
While there are a large number of these intrinsic functions, most applications use only a few of the operations.
HPF extrinsics
In order to allow the vendors with diverse architectures to provide their particular advantage, HPF included the capability to link "extrinsic" functions. These functions didn't need to be written in FORTRAN 90/HPF and performed a number of vendor-supported capabilities. This capability allowed users to perform such tasks as the creation of hybrid applications with some HPF and some message passing.
High performance computing programmers always like the ability to do things their own way in order to eke out that last drop of performance.
Heat Flow in HPF
To port our heat flow application to HPF, there is really only a single line of code that needs to be added. In the example below, we've changed to a larger two-dimensional array:
INTEGER PLATESIZ,MAXTIME
PARAMETER(PLATESIZ=2000,MAXTIME=200)
!HPF$ DISTRIBUTE PLATE(*,BLOCK)
REAL*4 PLATE(PLATESIZ,PLATESIZ)
INTEGER TICK
PLATE = 0.0
* Add Boundaries
PLATE(1,:) = 100.0
PLATE(PLATESIZ,:) = -40.0
PLATE(:,PLATESIZ) = 35.23
PLATE(:,1) = 4.5
DO TICK = 1,MAXTIME
PLATE(2:PLATESIZ-1,2:PLATESIZ-1) = (
+ PLATE(1:PLATESIZ-2,2:PLATESIZ-1) +
+ PLATE(3:PLATESIZ-0,2:PLATESIZ-1) +
+ PLATE(2:PLATESIZ-1,1:PLATESIZ-2) +
+ PLATE(2:PLATESIZ-1,3:PLATESIZ-0) ) / 4.0
PRINT 1000,TICK, PLATE(2,2)
1000 FORMAT('TICK = ',I5, F13.8)
ENDDO
*
END
You will notice that the HPF directive distributes the array columns using the BLOCK approach, keeping all the elements within a column on a single processor. At first glance, it might appear that (BLOCK,BLOCK) is the better distribution. However, there are two advantages to a (*,BLOCK) distribution. First, striding down a column is a unit-stride operation and so you might just as well process an entire column. The more significant aspect of the distribution is that a (BLOCK,BLOCK) distribution forces each processor to communicate with up to eight other processors to get its neighboring values. Using the (*,BLOCK) distribution, each processor will have to exchange data with at most two processors each time step.
When we look at PVM, we will look at this same program implemented in a SPMD-style message-passing fashion. In that example, you will see some of the details that HPF must handle to properly execute this code. After reviewing that code, you will probably choose to implement all of your future heat flow applications in HPF!
HPF Summary
In some ways, HPF has been good for FORTRAN 90. Companies such as IBM with its SP-1 needed to provide some high-level language for those users who didn't want to write message-passing codes. Because of this, IBM has invested a great deal of effort in implementing and optimizing HPF. Interestingly, much of this effort will directly benefit the ability to develop more sophisticated FORTRAN 90 compilers. The extensive data flow analysis required to minimize communications and manage the dynamic data structures will carry over into FORTRAN 90 compilers even without using the HPF directives.
Time will tell if the HPF data distribution directives will no longer be needed and compilers will be capable of performing sufficient analysis of straight FORTRAN 90 code to optimize data placement and movement.
In its current form, HPF is an excellent vehicle for expressing the highly data-parallel, grid-based applications. Its weaknesses are irregular communications and dynamic load balancing. A new effort to develop the next version of HPF is under way to address some of these issues. Unfortunately, it is more difficult to solve these runtime problems while maintaining good performance across a wide range of architectures.
Closing Notes
In this chapter, we have covered some of the efforts in the area of languages that have been developed to allow programs to be written for scalable computing. There is a tension between pure FORTRAN-77, FORTRAN 90, HPF, and message passing as to which will be the ultimate tools for scalable, high performance computing.
Certainly, there have been examples of great successes for both FORTRAN 90 (Thinking Machines CM-5) and HPF (IBM SP and others) as languages that can make excellent use of scalable computing systems. One of the problems of a high-level language approach is that sometimes using an abstract high-level language actually reduces effective portability.
The languages are designed to be portable, but if the vendor of your particular scalable computer doesn't support the language variant in which you have chosen to write your application, then it isn't portable. Even if the vendor has your language available, it may not be tuned to generate the best code for their architecture.
One solution is to purchase your compilers from a third-party company such as Pacific Sierra or Kuck and Associates. These vendors sell one compiler that runs across a wide range of systems. For users who can afford these options, these compilers afford a higher level of portability.
One of the fundamental issues is the chicken-and-egg problem. If users don't use a language, vendors won't improve the language. If all the influential users (with all the money) use message passing, then the existence of an excellent HPF compiler is of no real value to those users.
The good news is that both FORTRAN 90 and HPF provide one road map to portable scalable computing that doesn't require explicit message passing. The only question is which road we users will choose.
Footnotes
- There is another red-black approach that computes first the even elements and then the odd elements of the rod in two passes. This approach has no data dependencies within each pass. The ROD array never has all the values from the same time step. Either the odd or even values are one time step ahead of the other. It ends up with a stride of two and doubles the bandwidth but does not double the memory storage required to solve the problem.
- There are other algorithmic approaches to solving partial differential equations, such as the "fast multipole method" that accelerates convergence "legally." Don't assume that the brute force approach used here is the only method to solve this particular problem. Programmers should always look for the best available algorithm (parallel or not) before trying to scale up the "wrong" algorithm. For folks other than computer scientists, time to solution is more important than linear speed-up.
- One of the more significant efforts in the area of completely new languages is Streams and Iteration in a Single Assignment Language (SISAL). It's a data flow language that can easily integrate FORTRAN and C modules. The most interesting aspects of SISAL are the number of large computational codes that were ported to SISAL and the fact that the SISAL proponents generally compared their performance to the FORTRAN and C performance of the same applications.
- Just in case you are wondering, A*B gives you an element-wise multiplication of array members— not matrix multiplication. That is covered by a FORTRAN 90 intrinsic function.
- The distributed RC5 key-cracking effort was coordinated in this fashion. Each processor would check out a block of keys and begin testing those keys. At some point, if the processor was not fast enough or had crashed, the central system would reissue the block to another processor. This allowed the system to recover from problems on individual computers.
- As we shall soon see.
- Always a safe assumption.


