5.2: Message-Passing Environments
- Page ID
- 13443
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
A message-passing interface is a set of function and subroutine calls for C or FORTRAN that give you a way to split an application for parallel execution. Data is divided and passed out to other processors as messages. The receiving processors unpack them, do some work, and send the results back or pass them along to other processors in the parallel computer.
In some ways, message passing is the “assembly language” of parallel processing. You get ultimate responsibility, and if you are talented (and your problem cooperates), you get ultimate performance. If you have a nice scalable problem and are not satisfied with the resulting performance, you pretty much have yourself to blame. The compiler is completely unaware of the parallel aspects of the program.
The two most popular message-passing environments are parallel virtual machine (PVM) and message-passing interface (MPI). Most of the important features are available in either environment. Once you have mastered message passing, moving from PVM to MPI won’t cause you much trouble. You may also operate on a system that provides only a vendor-specific message-passing interface. However, once you understand message passing concepts and have properly decomposed your application, usually it’s not that much more effort to move from one message-passing library to another.1
Parallel Virtual Machine
The idea behind PVM is to assemble a diverse set of network-connected resources into a “virtual machine.” A user could marshal the resources of 35 idle workstations on the Internet and have their own personal scalable processing system. The work on PVM started in the early 1990s at Oak Ridge National Labs. PVM was pretty much an instant success among computer scientists. It provided a rough framework in which to experiment with using a network of workstations as a parallel processor.
In PVM Version 3, your virtual machine can consist of single processors, shared-memory multiprocessors, and scalable multiprocessors. PVM attempts to knit all of these resources into a single, consistent, execution environment.
To run PVM, you simply need a login account on a set of network computers that have the PVM software installed. You can even install it in your home directory. To create your own personal virtual machine, you would create a list of these computers in a file:
% cat hostfile
frodo.egr.msu.edu
gollum.egr.msu.edu
mordor.egr.msu.edu
%
After some nontrivial machinations with paths and environment variables, you can start the PVM console:
% pvm hostfile
pvmd already running.
pvm> conf
1 host, 1 data format
HOST DTID ARCH SPEED
frodo 40000 SUN4SOL2 1000
gollum 40001 SUN4SOL2 1000
mordor 40002 SUN4SOL2 1000
pvm> ps
HOST TID FLAG 0x COMMAND
frodo 40042 6/c,f pvmgs
pvm> reset
pvm> ps
HOST TID FLAG 0x COMMAND
pvm>
Many different users can be running virtual machines using the same pool of resources. Each user has their own view of an empty machine. The only way you might detect other virtual machines using your resources is in the percentage of the time your applications get the CPU.
There is a wide range of commands you can issue at the PVM console. The ps command shows the running processes in your virtual machine. It’s quite possible to have more processes than computer systems. Each process is time-shared on a system along with all the other load on the system. The reset command performs a soft reboot on your virtual machine. You are the virtual system administrator of the virtual machine you have assembled.
To execute programs on your virtual computer, you must compile and link your programs with the PVM library routines:2
% aimk mast slav
making in SUN4SOL2/ for SUN4SOL2
cc -O -I/opt/pvm3/include -DSYSVBFUNC -DSYSVSTR -DNOGETDTBLSIZ
-DSYSVSIGNAL -DNOWAIT3 -DNOUNIXDOM -o mast
../mast.c -L/opt/pvm3/lib/SUN4SOL2 -lpvm3 -lnsl -lsocket
mv mast ˜crs/pvm3/bin/SUN4SOL2
cc -O -I/opt/pvm3/include -DSYSVBFUNC -DSYSVSTR -DNOGETDTBLSIZ
-DSYSVSIGNAL -DNOWAIT3 -DNOUNIXDOM -o slav
../slav.c -L/opt/pvm3/lib/SUN4SOL2 -lpvm3 -lnsl -lsocket
mv slav ˜crs/pvm3/bin/SUN4SOL2
%
When the first PVM call is encountered, the application contacts your virtual machine and enrolls itself in the virtual machine. At that point it should show up in the output of the ps command issued at the PVM console.
From that point on, your application issues PVM calls to create more processes and interact with those processes. PVM takes the responsibility for distributing the processes on the different systems in the virtual machine, based on the load and your assessment of each system’s relative performance. Messages are moved across the network using user datagram protocol (UDP) and delivered to the appropriate process.
Typically, the PVM application starts up some additional PVM processes. These can be additional copies of the same program or each PVM process can run a different PVM application. Then the work is distributed among the processes, and results are gathered as necessary.
There are several basic models of computing that are typically used when working with PVM:
- Master/Slave: When operating in this mode, one process (usually the initial process) is designated as the master that spawns some number of worker processes. Work units are sent to each worker process, and the results are returned to the master. Often the master maintains a queue of work to be done and as a slave finishes, the master delivers a new work item to the slave. This approach works well when there is little data interaction and each work unit is independent. This approach has the advantage that the overall problem is naturally load-balanced even when there is some variation in the execution time of individual processes.
- Broadcast/Gather: This type of application is typically characterized by the fact that the shared data structure is relatively small and can be easily copied into every processor’s node. At the beginning of the time step, all the global data structures are broadcast from the master process to all of the processes. Each process then operates on their portion of the data. Each process produces a partial result that is sent back and gathered by the master process. This pattern is repeated for each time step.
- SPMD/Data decomposition: When the overall data structure is too large to have a copy stored in every process, it must be decomposed across multiple processes. Generally, at the beginning of a time step, all processes must exchange some data with each of their neighboring processes. Then with their local data augmented by the necessary subset of the remote data, they perform their computations. At the end of the time step, necessary data is again exchanged between neighboring processes, and the process is restarted.
The most complicated applications have nonuniform data flows and data that migrates around the system as the application changes and the load changes on the system.
In this section, we have two example programs: one is a master-slave operation, and the other is a data decomposition-style solution to the heat flow problem.
Queue of Tasks
In this example, one process (mast) creates five slave processes (slav) and doles out 20 work units (add one to a number). As a slave process responds, it’s given new work or told that all of the work units have been exhausted:
% cat mast.c
#include <stdio.h>
#include "pvm3.h"
#define MAXPROC 5
#define JOBS 20
main()
{
int mytid,info;
int tids[MAXPROC];
int tid,input,output,answers,work;
mytid = pvm_mytid();
info=pvm_spawn("slav", (char**)0, 0, "", MAXPROC, tids);
/* Send out the first work */
for(work=0;work<MAXPROC;work++) {
pvm_initsend(PvmDataDefault);
pvm_pkint(&work, 1, 1 ) ;
pvm_send(tids[work],1) ;/* 1 = msgtype */
}
/* Send out the rest of the work requests */
work = MAXPROC;
for(answers=0; answers < JOBS ; answers++) {
pvm_recv( -1, 2 ); /* -1 = any task 2 = msgtype */
pvm_upkint( &tid, 1, 1 );
pvm_upkint( &input, 1, 1 );
pvm_upkint( &output, 1, 1 );
printf("Thanks to %d 2*%d=%d\n",tid,input,output);
pvm_initsend(PvmDataDefault);
if ( work < JOBS ) {
pvm_pkint(&work, 1, 1 ) ;
work++;
} else {
input = -1;
pvm_pkint(&input, 1, 1 ) ; /* Tell them to stop */
}
pvm_send(tid,1) ;
}
pvm_exit();
}
%
One of the interesting aspects of the PVM interface is the separation of calls to prepare a new message, pack data into the message, and send the message. This is done for several reasons. PVM has the capability to convert between different floating-point formats, byte orderings, and character formats. This also allows a single message to have multiple data items with different types.
The purpose of the message type in each PVM send or receive is to allow the sender to wait for a particular type of message. In this example, we use two message types. Type one is a message from the master to the slave, and type two is the response.
When performing a receive, a process can either wait for a message from a specific process or a message from any process.
In the second phase of the computation, the master waits for a response from any slave, prints the response, and then doles out another work unit to the slave or tells the slave to terminate by sending a message with a value of -1.
The slave code is quite simple — it waits for a message, unpacks it, checks to see if it is a termination message, returns a response, and repeats:
% cat slav.c
#include <stdio.h>
#include "pvm3.h"
/* A simple program to double integers */
main()
{
int mytid;
int input,output;
mytid = pvm_mytid();
while(1) {
pvm_recv( -1, 1 ); /* -1 = any task 1=msgtype */
pvm_upkint(&input, 1, 1);
if ( input == -1 ) break; /* All done */
output = input * 2;
pvm_initsend( PvmDataDefault );
pvm_pkint( &mytid, 1, 1 );
pvm_pkint( &input, 1, 1 );
pvm_pkint( &output, 1, 1 );
pvm_send( pvm_parent(), 2 );
}
pvm_exit();
}
%
When the master program is executed, it produces the following output:
% pheat
Thanks to 262204 2*0=0
Thanks to 262205 2*1=2
Thanks to 262206 2*2=4
Thanks to 262207 2*3=6
Thanks to 262204 2*5=10
Thanks to 262205 2*6=12
Thanks to 262206 2*7=14
Thanks to 262207 2*8=16
Thanks to 262204 2*9=18
Thanks to 262205 2*10=20
Thanks to 262206 2*11=22
Thanks to 262207 2*12=24
Thanks to 262205 2*14=28
Thanks to 262207 2*16=32
Thanks to 262205 2*17=34
Thanks to 262207 2*18=36
Thanks to 262204 2*13=26
Thanks to 262205 2*19=38
Thanks to 262206 2*15=30
Thanks to 262208 2*4=8
%
Clearly the processes are operating in parallel, and the order of execution is somewhat random. This code is an excellent skeleton for handling a wide range of computations. In the next example, we perform an SPMD-style computation to solve the heat flow problem using PVM.
Heat Flow in PVM
This next example is a rather complicated application that implements the heat flow problem in PVM. In many ways, it gives some insight into the work that is performed by the HPF environment. We will solve a heat flow in a two-dimensional plate with four heat sources and the edges in zero-degree water, as shown in [Figure 1].
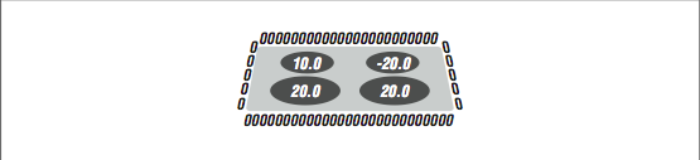
The data will be spread across all of the processes using a (*, BLOCK) distribution. Columns are distributed to processes in contiguous blocks, and all the row elements in a column are stored on the same process. As with HPF, the process that “owns” a data cell performs the computations for that cell after retrieving any data necessary to perform the computation.
We use a red-black approach but for simplicity, we copy the data back at the end of each iteration. For a true red-black, you would perform the computation in the opposite direction every other time step.
Note that instead of spawning slave process, the parent process spawns additional copies of itself. This is typical of SPMD-style programs. Once the additional processes have been spawned, all the processes wait at a barrier before they look for the process numbers of the members of the group. Once the processes have arrived at the barrier, they all retrieve a list of the different process numbers:
% cat pheat.f
PROGRAM PHEAT
INCLUDE ’../include/fpvm3.h’
INTEGER NPROC,ROWS,COLS,TOTCOLS,OFFSET
PARAMETER(NPROC=4,MAXTIME=200)
PARAMETER(ROWS=200,TOTCOLS=200)
PARAMETER(COLS=(TOTCOLS/NPROC)+3)
REAL*8 RED(0:ROWS+1,0:COLS+1), BLACK(0:ROWS+1,0:COLS+1)
LOGICAL IAMFIRST,IAMLAST
INTEGER INUM,INFO,TIDS(0:NPROC-1),IERR
INTEGER I,R,C
INTEGER TICK,MAXTIME
CHARACTER*30 FNAME
* Get the SPMD thing going - Join the pheat group
CALL PVMFJOINGROUP(’pheat’, INUM)
* If we are the first in the pheat group, make some helpers
IF ( INUM.EQ.0 ) THEN
DO I=1,NPROC-1
CALL PVMFSPAWN(’pheat’, 0, ’anywhere’, 1, TIDS(I), IERR)
ENDDO
ENDIF
* Barrier to make sure we are all here so we can look them up
CALL PVMFBARRIER( ’pheat’, NPROC, INFO )
* Find my pals and get their TIDs - TIDS are necessary for sending
DO I=0,NPROC-1
CALL PVMFGETTID(’pheat’, I, TIDS(I))
ENDDO
At this point in the code, we have NPROC processes executing in an SPMD mode. The next step is to determine which subset of the array each process will compute. This is driven by the INUM variable, which ranges from 0 to 3 and uniquely identifies these processes.
We decompose the data and store only one quarter of the data on each process. Using the INUM variable, we choose our continuous set of columns to store and compute. The OFFSET variable maps between a “global” column in the entire array and a local column in our local subset of the array. [Figure 2] shows a map that indicates which processors store which data elements. The values marked with a B are boundary values and won’t change during the simulation. They are all set to 0. This code is often rather tricky to figure out. Performing a (BLOCK, BLOCK) distribution requires a two-dimensional decomposition and exchanging data with the neighbors above and below, in addition to the neighbors to the left and right:
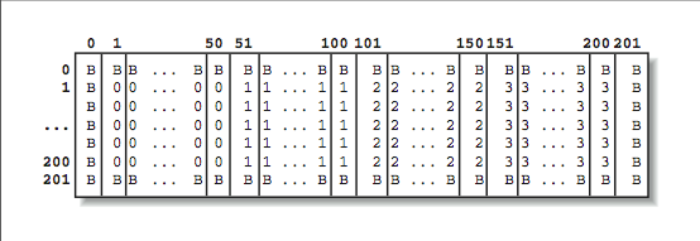
* Compute my geometry - What subset do I process? (INUM=0 values)
* Actual Column = OFFSET + Column (OFFSET = 0)
* Column 0 = neighbors from left
* Column 1 = send to left
* Columns 1..mylen My cells to compute
* Column mylen = Send to right (mylen=50)
* Column mylen+1 = Neighbors from Right (Column 51)
IAMFIRST = (INUM .EQ. 0)
IAMLAST = (INUM .EQ. NPROC-1)
OFFSET = (ROWS/NPROC * INUM )
MYLEN = ROWS/NPROC
IF ( IAMLAST ) MYLEN = TOTCOLS - OFFSET
PRINT *,’INUM:’,INUM,’ Local’,1,MYLEN,
+ ’ Global’,OFFSET+1,OFFSET+MYLEN
* Start Cold
DO C=0,COLS+1
DO R=0,ROWS+1
BLACK(R,C) = 0.0
ENDDO
ENDDO
Now we run the time steps. The first act in each time step is to reset the heat sources. In this simulation, we have four heat sources placed near the middle of the plate. We must restore all the values each time through the simulation as they are modified in the main loop:
* Begin running the time steps
DO TICK=1,MAXTIME
* Set the heat persistent sources
CALL STORE(BLACK,ROWS,COLS,OFFSET,MYLEN,
+ ROWS/3,TOTCOLS/3,10.0,INUM)
CALL STORE(BLACK,ROWS,COLS,OFFSET,MYLEN,
+ 2*ROWS/3,TOTCOLS/3,20.0,INUM)
CALL STORE(BLACK,ROWS,COLS,OFFSET,MYLEN,
+ ROWS/3,2*TOTCOLS/3,-20.0,INUM)
CALL STORE(BLACK,ROWS,COLS,OFFSET,MYLEN,
+ 2*ROWS/3,2*TOTCOLS/3,20.0,INUM)
Now we perform the exchange of the “ghost values” with our neighboring processes. For example, Process 0 contains the elements for global column 50. To compute the next time step values for column 50, we need column 51, which is stored in Process 1. Similarly, before Process 1 can compute the new values for column 51, it needs Process 0’s values for column 50.
[Figure 3] shows how the data is transferred between processors. Each process sends its leftmost column to the left and its rightmost column to the right. Because the first and last processes border unchanging boundary values on the left and right respectively, this is not necessary for columns one and 200. If all is done properly, each process can receive its ghost values from their left and right neighbors.
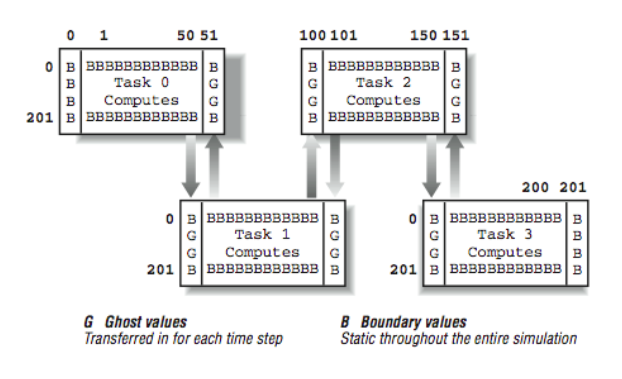
The net result of all of the transfers is that for each space that must be computed, it’s surrounded by one layer of either boundary values or ghost values from the right or left neighbors:
* Send left and right
IF ( .NOT. IAMFIRST ) THEN
CALL PVMFINITSEND(PVMDEFAULT,TRUE)
CALL PVMFPACK( REAL8, BLACK(1,1), ROWS, 1, INFO )
CALL PVMFSEND( TIDS(INUM-1), 1, INFO )
ENDIF
IF ( .NOT. IAMLAST ) THEN
CALL PVMFINITSEND(PVMDEFAULT,TRUE)
CALL PVMFPACK( REAL8, BLACK(1,MYLEN), ROWS, 1, INFO )
CALL PVMFSEND( TIDS(INUM+1), 2, INFO )
ENDIF
* Receive right, then left
IF ( .NOT. IAMLAST ) THEN
CALL PVMFRECV( TIDS(INUM+1), 1, BUFID )
CALL PVMFUNPACK ( REAL8, BLACK(1,MYLEN+1), ROWS, 1, INFO
ENDIF
IF ( .NOT. IAMFIRST ) THEN
CALL PVMFRECV( TIDS(INUM-1), 2, BUFID )
CALL PVMFUNPACK ( REAL8, BLACK(1,0), ROWS, 1, INFO)
ENDIF
This next segment is the easy part. All the appropriate ghost values are in place, so we must simply perform the computation in our subspace. At the end, we copy back from the RED to the BLACK array; in a real simulation, we would perform two time steps, one from BLACK to RED and the other from RED to BLACK, to save this extra copy:
* Perform the flow
DO C=1,MYLEN
DO R=1,ROWS
RED(R,C) = ( BLACK(R,C) +
+ BLACK(R,C-1) + BLACK(R-1,C) +
+ BLACK(R+1,C) + BLACK(R,C+1) ) / 5.0
ENDDO
ENDDO
* Copy back - Normally we would do a red and black version of the loop
DO C=1,MYLEN
DO R=1,ROWS
BLACK(R,C) = RED(R,C)
ENDDO
ENDDO
ENDDO
Now we find the center cell and send to the master process (if necessary) so it can be printed out. We also dump out the data into files for debugging or later visualization of the results. Each file is made unique by appending the instance number to the filename. Then the program terminates:
CALL SENDCELL(RED,ROWS,COLS,OFFSET,MYLEN,INUM,TIDS(0),
+ ROWS/2,TOTCOLS/2)
* Dump out data for verification
IF ( ROWS .LE. 20 ) THEN
FNAME = ’/tmp/pheatout.’ // CHAR(ICHAR(’0’)+INUM)
OPEN(UNIT=9,NAME=FNAME,FORM=’formatted’)
DO C=1,MYLEN
WRITE(9,100)(BLACK(R,C),R=1,ROWS)
100 FORMAT(20F12.6)
ENDDO
CLOSE(UNIT=9)
ENDIF
* Lets all go together
CALL PVMFBARRIER( ’pheat’, NPROC, INFO )
CALL PVMFEXIT( INFO )
END
The SENDCELL routine finds a particular cell and prints it out on the master process. This routine is called in an SPMD style: all the processes enter this routine although all not at precisely the same time. Depending on the INUM and the cell that we are looking for, each process may do something different.
If the cell in question is in the master process, and we are the master process, print it out. All other processes do nothing. If the cell in question is stored in another process, the process with the cell sends it to the master processes. The master process receives the value and prints it out. All the other processes do nothing.
This is a simple example of the typical style of SPMD code. All the processes execute the code at roughly the same time, but, based on information local to each process, the actions performed by different processes may be quite different:
SUBROUTINE SENDCELL(RED,ROWS,COLS,OFFSET,MYLEN,INUM,PTID,R,C)
INCLUDE ’../include/fpvm3.h’
INTEGER ROWS,COLS,OFFSET,MYLEN,INUM,PTID,R,C
REAL*8 RED(0:ROWS+1,0:COLS+1)
REAL*8 CENTER
* Compute local row number to determine if it is ours
I = C - OFFSET
IF ( I .GE. 1 .AND. I.LE. MYLEN ) THEN
IF ( INUM .EQ. 0 ) THEN
PRINT *,’Master has’, RED(R,I), R, C, I
ELSE
CALL PVMFINITSEND(PVMDEFAULT,TRUE)
CALL PVMFPACK( REAL8, RED(R,I), 1, 1, INFO )
PRINT *, ’INUM:’,INUM,’ Returning’,R,C,RED(R,I),I
CALL PVMFSEND( PTID, 3, INFO )
ENDIF
ELSE
IF ( INUM .EQ. 0 ) THEN
CALL PVMFRECV( -1 , 3, BUFID )
CALL PVMFUNPACK ( REAL8, CENTER, 1, 1, INFO)
PRINT *, ’Master Received’,R,C,CENTER
ENDIF
ENDIF
RETURN
END
Like the previous routine, the STORE routine is executed on all processes. The idea is to store a value into a global row and column position. First, we must determine if the cell is even in our process. If the cell is in our process, we must compute the local column (I) in our subset of the overall matrix and then store the value:
SUBROUTINE STORE(RED,ROWS,COLS,OFFSET,MYLEN,R,C,VALUE,INUM)
REAL*8 RED(0:ROWS+1,0:COLS+1)
REAL VALUE
INTEGER ROWS,COLS,OFFSET,MYLEN,R,C,I,INUM
I = C - OFFSET
IF ( I .LT. 1 .OR. I .GT. MYLEN ) RETURN
RED(R,I) = VALUE
RETURN
END
When this program executes, it has the following output:
% pheat
INUM: 0 Local 1 50 Global 1 50
Master Received 100 100 3.4722390023541D-07
%
We see two lines of print. The first line indicates the values that Process 0 used in its geometry computation. The second line is the output from the master process of the temperature at cell (100,100) after 200 time steps.
One interesting technique that is useful for debugging this type of program is to change the number of processes that are created. If the program is not quite moving its data properly, you usually get different results when different numbers of processes are used. If you look closely, the above code performs correctly with one process or 30 processes.
Notice that there is no barrier operation at the end of each time step. This is in contrast to the way parallel loops operate on shared uniform memory multiprocessors that force a barrier at the end of each loop. Because we have used an “owner computes” rule, and nothing is computed until all the required ghost data is received, there is no need for a barrier. The receipt of the messages with the proper ghost values allows a process to begin computing immediately without regard to what the other processes are currently doing.
This example can be used either as a framework for developing other grid-based computations, or as a good excuse to use HPF and appreciate the hard work that the HPF compiler developers have done. A well-done HPF implementation of this simulation should outperform the PVM implementation because HPF can make tighter optimizations. Unlike us, the HPF compiler doesn’t have to keep its generated code readable.
PVM Summary
PVM is a widely used tool because it affords portability across every architecture other than SIMD. Once the effort has been invested in making a code message passing, it tends to run well on many architectures.
The primary complaints about PVM include:
- The need for a pack step separate from the send step
- The fact that it is designed to work in a heterogeneous environment that may incur some overhead
- It doesn’t automate common tasks such as geometry computations
But all in all, for a certain set of programmers, PVM is the tool to use. If you would like to learn more about PVM see PVM — A User’s Guide and Tutorial for Networked Parallel Computing, by Al Geist, Adam Beguelin, Jack Dongarra, Weicheng Jiang, Robert Manchek, and Vaidy Sunderam (MIT Press). Information is also available at www.netlib.org/pvm3/.
Message-Passing Interface
The Message-Passing Interface (MPI) was designed to be an industrial-strength message-passing environment that is portable across a wide range of hardware environments.
Much like High Performance FORTRAN, MPI was developed by a group of computer vendors, application developers, and computer scientists. The idea was to come up with a specification that would take the strengths of many of the existing proprietary message passing environments on a wide variety of architectures and come up with a specification that could be implemented on architectures ranging from SIMD systems with thousands of small processors to MIMD networks of workstations and everything in between.
Interestingly, the MPI effort was completed a year after the High Performance FORTRAN (HPF) effort was completed. Some viewed MPI as a portable message-passing interface that could support a good HPF compiler. Having MPI makes the compiler more portable. Also having the compiler use MPI as its message-passing environment insures that MPI is heavily tested and that sufficient resources are invested into the MPI implementation.
PVM Versus MPI
While many of the folks involved in PVM participated in the MPI effort, MPI is not simply a follow-on to PVM. PVM was developed in a university/research lab environment and evolved over time as new features were needed. For example, the group capability was not designed into PVM at a fundamental level. Some of the underlying assumptions of PVM were based “on a network of workstations connected via Ethernet” model and didn’t export well to scalable computers.3 In some ways, MPI is more robust than PVM, and in other ways, MPI is simpler than PVM. MPI doesn’t specify the system management details as in PVM; MPI doesn’t specify how a virtual machine is to be created, operated, and used.
MPI Features
MPI has a number of useful features beyond the basic send and receive capabilities. These include:
- Communicators: A communicator is a subset of the active processes that can be treated as a group for collective operations such as broadcast, reduction, barriers, sending, or receiving. Within each communicator, a process has a rank that ranges from zero to the size of the group. A process may be a member of more than one communicator and have a different rank within each communicator. There is a default communicator that refers to all the MPI processes that is called
MPI_COMM_WORLD. - Topologies: A communicator can have a topology associated with it. This arranges the processes that belong to a communicator into some layout. The most common layout is a Cartesian decomposition. For example, 12 processes may be arranged into a 3×4 grid.4 Once these topologies are defined, they can be queried to find the neighboring processes in the topology. In addition to the Cartesian (grid) topology, MPI also supports a graph-based topology.
- Communication modes: MPI supports multiple styles of communication, including blocking and non- blocking. Users can also choose to use explicit buffers for sending or allow MPI to manage the buffers. The nonblocking capabilities allow the overlap of communication and computation. MPI can support a model in which there is no available memory space for buffers and the data must be copied directly from the address space of the sending process to the memory space of the receiving process. MPI also supports a single call to perform a send and receive that is quite useful when processes need to exchange data.
- Single-call collective operations: Some of the calls in MPI automate collective operations in a single call. For example, the broadcast operation sends values from the master to the slaves and receives the values on the slaves in the same operation. The net result is that the values are updated on all processes. Similarly, there is a single call to sum a value across all of the processes to a single value. By bundling all this functionality into a single call, systems that have support for collective operations in hardware can make best use of this hardware. Also, when MPI is operating on a shared-memory environment, the broadcast can be simplified as all the slaves simply make a local copy of a shared variable.
Clearly, the developers of the MPI specification had significant experience with developing message-passing applications and added many widely used features to the message-passing library. Without these features, each programmer needed to use more primitive operations to construct their own versions of the higher-level operations.
Heat Flow in MPI
In this example, we implement our heat flow problem in MPI using a similar decomposition to the PVM example. There are several ways to approach the problem. We could almost translate PVM calls to corresponding MPI calls using the MPI_COMM_WORLD communicator. However, to showcase some of the MPI features, we create a Cartesian communicator:
PROGRAM MHEATC
INCLUDE ’mpif.h’
INCLUDE ’mpef.h’
INTEGER ROWS,COLS,TOTCOLS
PARAMETER(MAXTIME=200)
* This simulation can be run on MINPROC or greater processes.
* It is OK to set MINPROC to 1 for testing purposes
* For a large number of rows and columns, it is best to set MINPROC
* to the actual number of runtime processes
PARAMETER(MINPROC=2) PARAMETER(ROWS=200,TOTCOLS=200,COLS=TOTCOLS/MINPROC)
DOUBLE PRECISION RED(0:ROWS+1,0:COLS+1),BLACK(0:ROWS+1,0:COLS+1)
INTEGER S,E,MYLEN,R,C
INTEGER TICK,MAXTIME
CHARACTER*30 FNAME
The basic data structures are much the same as in the PVM example. We allocate a subset of the heat arrays in each process. In this example, the amount of space allocated in each process is set by the compile-time variable MINPROC. The simulation can execute on more than MINPROC processes (wasting some space in each process), but it can’t execute on less than MINPROC processes, or there won’t be sufficient total space across all of the processes to hold the array:
INTEGER COMM1D,INUM,NPROC,IERR
INTEGER DIMS(1),COORDS(1)
LOGICAL PERIODS(1)
LOGICAL REORDER
INTEGER NDIM
INTEGER STATUS(MPI_STATUS_SIZE)
INTEGER RIGHTPROC, LEFTPROC
These data structures are used for our interaction with MPI. As we will be doing a one-dimensional Cartesian decomposition, our arrays are dimensioned to one. If you were to do a two-dimensional decomposition, these arrays would need two elements:
PRINT *,’Calling MPI_INIT’
CALL MPI_INIT( IERR )
PRINT *,’Back from MPI_INIT’
CALL MPI_COMM_SIZE( MPI_COMM_WORLD, NPROC, IERR )
The call to MPI_INIT creates the appropriate number of processes. Note that in the output, the PRINT statement before the call only appears once, but the second PRINT appears once for each process. We call MPI_COMM_SIZE to determine the size of the global communicator MPI_COMM_WORLD. We use this value to set up our Cartesian topology:
* Create new communicator that has a Cartesian topology associated
* with it - MPI_CART_CREATE returns COMM1D - A communicator descriptor
DIMS(1) = NPROC
PERIODS(1) = .FALSE.
REORDER = .TRUE.
NDIM = 1
CALL MPI_CART_CREATE(MPI_COMM_WORLD, NDIM, DIMS, PERIODS,
+ REORDER, COMM1D, IERR)
Now we create a one-dimensional (NDIM=1) arrangement of all of our processes (MPI_COMM_WORLD). All of the parameters on this call are input values except for COMM1D and IERR. COMM1D is an integer “communicator handle.” If you print it out, it will be a value such as 134. It is not actually data, it is merely a handle that is used in other calls. It is quite similar to a file descriptor or unit number used when performing input-output to and from files.
The topology we use is a one-dimensional decomposition that isn’t periodic. If we specified that we wanted a periodic decomposition, the far-left and far-right processes would be neighbors in a wrapped-around fashion making a ring. Given that it isn’t periodic, the far-left and far-right processes have no neighbors.
In our PVM example above, we declared that Process 0 was the far-right process, Process NPROC-1 was the far-left process, and the other processes were arranged linearly between those two. If we set REORDER to .FALSE., MPI also chooses this arrangement. However, if we set REORDER to .TRUE., MPI may choose to arrange the processes in some other fashion to achieve better performance, assuming that you are communicating with close neighbors.
Once the communicator is set up, we use it in all of our communication operations:
* Get my rank in the new communicator
CALL MPI_COMM_RANK( COMM1D, INUM, IERR)
Within each communicator, each process has a rank from zero to the size of the communicator minus 1. The MPI_COMM_RANK tells each process its rank within the communicator. A process may have a different rank in the COMM1D communicator than in the MPI_COMM_WORLD communicator because of some reordering.
Given a Cartesian topology communicator,5 we can extract information from the communicator using the MPI_CART_GET routine:
* Given a communicator handle COMM1D, get the topology, and my position
* in the topology
CALL MPI_CART_GET(COMM1D, NDIM, DIMS, PERIODS, COORDS, IERR)
In this call, all of the parameters are output values rather than input values as in the MPI_CART_CREATE call. The COORDS variable tells us our coordinates within the communicator. This is not so useful in our one-dimensional example, but in a two-dimensional process decomposition, it would tell our current position in that two-dimensional grid:
* Returns the left and right neighbors 1 unit away in the zeroth dimension
* of our Cartesian map - since we are not periodic, our neighbors may
* not always exist - MPI_CART_SHIFT handles this for us
CALL MPI_CART_SHIFT(COMM1D, 0, 1, LEFTPROC, RIGHTPROC, IERR)
CALL MPE_DECOMP1D(TOTCOLS, NPROC, INUM, S, E)
MYLEN = ( E - S ) + 1
IF ( MYLEN.GT.COLS ) THEN
PRINT *,’Not enough space, need’,MYLEN,’ have ’,COLS
PRINT *,TOTCOLS,NPROC,INUM,S,E
STOP
ENDIF
PRINT *,INUM,NPROC,COORDS(1),LEFTPROC,RIGHTPROC, S, E
We can use MPI_CART_SHIFT to determine the rank number of our left and right neighbors, so we can exchange our common points with these neighbors. This is necessary because we can’t simply send to INUM-1 and INUM+1 if MPI has chosen to reorder our Cartesian decomposition. If we are the far-left or far-right process, the neighbor that doesn’t exist is set to MPI_PROC_NULL, which indicates that we have no neighbor. Later when we are performing message sending, it checks this value and sends messages only to real processes. By not sending the message to the “null process,” MPI has saved us an IF test.
To determine which strip of the global array we store and compute in this process, we call a utility routine called MPE_DECOMP1D that simply does several calculations to evenly split our 200 columns among our processes in contiguous strips. In the PVM version, we need to perform this computation by hand.
The MPE_DECOMP1D routine is an example of an extended MPI library call (hence the MPE prefix). These extensions include graphics support and logging tools in addition to some general utilities. The MPE library consists of routines that were useful enough to standardize but not required to be supported by all MPI implementations. You will find the MPE routines supported on most MPI implementations.
Now that we have our communicator group set up, and we know which strip each process will handle, we begin the computation:
* Start Cold
DO C=0,COLS+1
DO R=0,ROWS+1
BLACK(R,C) = 0.0
ENDDO
ENDDO
As in the PVM example, we set the plate (including boundary values) to zero.
All processes begin the time step loop. Interestingly, like in PVM, there is no need for any synchronization. The messages implicitly synchronize our loops.
The first step is to store the permanent heat sources. We need to use a routine because we must make the store operations relative to our strip of the global array:
* Begin running the time steps
DO TICK=1,MAXTIME
* Set the persistent heat sources
CALL STORE(BLACK,ROWS,COLS,S,E,ROWS/3,TOTCOLS/3,10.0,INUM)
CALL STORE(BLACK,ROWS,COLS,S,E,2*ROWS/3,TOTCOLS/3,20.0,INUM)
CALL STORE(BLACK,ROWS,COLS,S,E,ROWS/3,2*TOTCOLS/3,-20.0,INUM)
CALL STORE(BLACK,ROWS,COLS,S,E,2*ROWS/3,2*TOTCOLS/3,20.0,INUM)
All of the processes set these values independently depending on which process has which strip of the overall array.
Now we exchange the data with our neighbors as determined by the Cartesian communicator. Note that we don’t need an IF test to determine if we are the far-left or far-right process. If we are at the edge, our neighbor setting is MPI_PROC_NULL and the MPI_SEND and MPI_RECV calls do nothing when given this as a source or destination value, thus saving us an IF test.
Note that we specify the communicator COMM1D because the rank values we are using in these calls are relative to that communicator:
* Send left and receive right
CALL MPI_SEND(BLACK(1,1),ROWS,MPI_DOUBLE_PRECISION,
+ LEFTPROC,1,COMM1D,IERR)
CALL MPI_RECV(BLACK(1,MYLEN+1),ROWS,MPI_DOUBLE_PRECISION,
+ RIGHTPROC,1,COMM1D,STATUS,IERR)
* Send Right and Receive left in a single statement
CALL MPI_SENDRECV(
+ BLACK(1,MYLEN),ROWS,COMM1D,RIGHTPROC,2,
+ BLACK(1,0),ROWS,COMM1D,LEFTPROC, 2,
+ MPI_COMM_WORLD, STATUS, IERR)
Just to show off, we use both the separate send and receive, and the combined send and receive. When given a choice, it’s probably a good idea to use the combined operations to give the runtime environment more flexibility in terms of buffering. One downside to this that occurs on a network of workstations (or any other high-latency interconnect) is that you can’t do both send operations first and then do both receive operations to overlap some of the communication delay.
Once we have all of our ghost points from our neighbors, we can perform the algorithm on our subset of the space:
* Perform the flow
DO C=1,MYLEN
DO R=1,ROWS
RED(R,C) = ( BLACK(R,C) +
+ BLACK(R,C-1) + BLACK(R-1,C) +
+ BLACK(R+1,C) + BLACK(R,C+1) ) / 5.0
ENDDO
ENDDO
* Copy back - Normally we would do a red and black version of the loop
DO C=1,MYLEN
DO R=1,ROWS
BLACK(R,C) = RED(R,C)
ENDDO
ENDDO
ENDDO
Again, for simplicity, we don’t do the complete red-black computation.6 We have no synchronization at the bottom of the loop because the messages implicitly synchronize the processes at the top of the next loop.
Again, we dump out the data for verification. As in the PVM example, one good test of basic correctness is to make sure you get exactly the same results for varying numbers of processes:
* Dump out data for verification
IF ( ROWS .LE. 20 ) THEN
FNAME = ’/tmp/mheatcout.’ // CHAR(ICHAR(’0’)+INUM)
OPEN(UNIT=9,NAME=FNAME,FORM=’formatted’)
DO C=1,MYLEN
WRITE(9,100)(BLACK(R,C),R=1,ROWS)
100 FORMAT(20F12.6)
ENDDO
CLOSE(UNIT=9)
ENDIF
To terminate the program, we call MPI_FINALIZE:
* Lets all go together
CALL MPI_FINALIZE(IERR)
END
As in the PVM example, we need a routine to store a value into the proper strip of the global array. This routine simply checks to see if a particular global element is in this process and if so, computes the proper location within its strip for the value. If the global element is not in this process, this routine simply returns doing nothing:
SUBROUTINE STORE(RED,ROWS,COLS,S,E,R,C,VALUE,INUM)
REAL*8 RED(0:ROWS+1,0:COLS+1)
REAL VALUE
INTEGER ROWS,COLS,S,E,R,C,I,INUM
IF ( C .LT. S .OR. C .GT. E ) RETURN
I = ( C - S ) + 1
* PRINT *,’STORE, INUM,R,C,S,E,R,I’,INUM,R,C,S,E,R,I,VALUE RED(R,I) = VALUE
RETURN
END
When this program is executed, it has the following output:
% mpif77 -c mheatc.f mheatc.f:
MAIN mheatc:
store:
% mpif77 -o mheatc mheatc.o -lmpe
% mheatc -np 4
Calling MPI_INIT
Back from MPI_INIT
Back from MPI_INIT
Back from MPI_INIT
Back from MPI_INIT
0 4 0 -1 1 1 50
2 4 2 1 3 101 150
3 4 3 2 -1 151 200
1 4 1 0 2 51 100
%
As you can see, we call MPI_INIT to activate the four processes. The PRINT statement immediately after the MPI_INIT call appears four times, once for each of the activated processes. Then each process prints out the strip of the array it will process. We can also see the neighbors of each process including -1 when a process has no neighbor to the left or right. Notice that Process 0 has no left neighbor, and Process 3 has no right neighbor. MPI has provided us the utilities to simplify message-passing code that we need to add to implement this type of grid- based application.
When you compare this example with a PVM implementation of the same problem, you can see some of the contrasts between the two approaches. Programmers who wrote the same six lines of code over and over in PVM combined them into a single call in MPI. In MPI, you can think “data parallel” and express your program in a more data-parallel fashion.
In some ways, MPI feels less like assembly language than PVM. However, MPI does take a little getting used to when compared to PVM. The concept of a Cartesian communicator may seem foreign at first, but with understanding, it becomes a flexible and powerful tool.
Heat in MPI Using Broadcast/Gather
One style of parallel programming that we have not yet seen is the broadcast/gather style. Not all applications can be naturally solved using this style of programming. However, if an application can use this approach effectively, the amount of modification that is required to make a code run in a message-passing environment is minimal.
Applications that most benefit from this approach generally do a lot of computation using some small amount of shared information. One requirement is that one complete copy of the “shared” information must fit in each of the processes.
If we keep our grid size small enough, we can actually program our heat flow application using this approach. This is almost certainly a less efficient implementation than any of the earlier implementations of this problem because the core computation is so simple. However, if the core computations were more complex and needed access to values farther than one unit away, this might be a good approach.
The data structures are simpler for this approach and, actually, are no different than the single-process FORTRAN 90 or HPF versions. We will allocate a complete RED and BLACK array in every process:
PROGRAM MHEAT
INCLUDE ’mpif.h’
INCLUDE ’mpef.h’
INTEGER ROWS,COLS
PARAMETER(MAXTIME=200)
PARAMETER(ROWS=200,COLS=200)
DOUBLE PRECISION RED(0:ROWS+1,0:COLS+1),BLACK(0:ROWS+1,0:COLS+1)
We need fewer variables for the MPI calls because we aren’t creating a communicator. We simply use the default communicator MPI_COMM_WORLD. We start up our processes, and find the size and rank of our process group:
INTEGER INUM,NPROC,IERR,SRC,DEST,TAG
INTEGER S,E,LS,LE,MYLEN
INTEGER STATUS(MPI_STATUS_SIZE)
INTEGER I,R,C
INTEGER TICK,MAXTIME
CHARACTER*30 FNAME
PRINT *,’Calling MPI_INIT’
CALL MPI_INIT( IERR )
CALL MPI_COMM_SIZE( MPI_COMM_WORLD, NPROC, IERR )
CALL MPI_COMM_RANK( MPI_COMM_WORLD, INUM, IERR)
CALL MPE_DECOMP1D(COLS, NPROC, INUM, S, E, IERR)
PRINT *,’My Share ’, INUM, NPROC, S, E
Since we are broadcasting initial values to all of the processes, we only have to set things up on the master process:
* Start Cold
IF ( INUM.EQ.0 ) THEN
DO C=0,COLS+1
DO R=0,ROWS+1
BLACK(R,C) = 0.0
ENDDO
ENDDO
ENDIF
As we run the time steps (again with no synchronization), we set the persistent heat sources directly. Since the shape of the data structure is the same in the master and all other processes, we can use the real array coordinates rather than mapping them as with the previous examples. We could skip the persistent settings on the nonmaster processes, but it doesn’t hurt to do it on all processes:
* Begin running the time steps
DO TICK=1,MAXTIME
* Set the heat sources
BLACK(ROWS/3, COLS/3)= 10.0
BLACK(2*ROWS/3, COLS/3) = 20.0
BLACK(ROWS/3, 2*COLS/3) = -20.0
BLACK(2*ROWS/3, 2*COLS/3) = 20.0
Now we broadcast the entire array from process rank zero to all of the other processes in the MPI_COMM_WORLD communicator. Note that this call does the sending on rank zero process and receiving on the other processes. The net result of this call is that all the processes have the values formerly in the master process in a single call:
* Broadcast the array
CALL MPI_BCAST(BLACK,(ROWS+2)*(COLS+2),MPI_DOUBLE_PRECISION,
+ 0,MPI_COMM_WORLD,IERR)
Now we perform the subset computation on each process. Note that we are using global coordinates because the array has the same shape on each of the processes. All we need to do is make sure we set up our particular strip of columns according to S and E:
* Perform the flow on our subset
DO C=S,E
DO R=1,ROWS
RED(R,C) = ( BLACK(R,C) +
+ BLACK(R,C-1) + BLACK(R-1,C) +
+ BLACK(R+1,C) + BLACK(R,C+1) ) / 5.0
ENDDO
ENDDO
Now we need to gather the appropriate strips from the processes into the appropriate strip in the master array for rebroadcast in the next time step. We could change the loop in the master to receive the messages in any order and check the STATUS variable to see which strip it received:
* Gather back up into the BLACK array in master (INUM = 0)
IF ( INUM .EQ. 0 ) THEN
DO C=S,E
DO R=1,ROWS
BLACK(R,C) = RED(R,C)
ENDDO
ENDDO
DO I=1,NPROC-1
CALL MPE_DECOMP1D(COLS, NPROC, I, LS, LE, IERR)
MYLEN = ( LE - LS ) + 1
SRC = I TAG = 0
CALL MPI_RECV(BLACK(0,LS),MYLEN*(ROWS+2),
+ MPI_DOUBLE_PRECISION, SRC, TAG,
+ MPI_COMM_WORLD, STATUS, IERR)
* Print *,’Recv’,I,MYLEN
ENDDO
ELSE
MYLEN = ( E - S ) + 1
DEST = 0
TAG = 0
CALL MPI_SEND(RED(0,S),MYLEN*(ROWS+2),MPI_DOUBLE_PRECISION,
+ DEST, TAG, MPI_COMM_WORLD, IERR)
Print *,’Send’,INUM,MYLEN
ENDIF
ENDDO
We use MPE_DECOMP1D to determine which strip we’re receiving from each process.
In some applications, the value that must be gathered is a sum or another single value. To accomplish this, you can use one of the MPI reduction routines that coalesce a set of distributed values into a single value using a single call.
Again at the end, we dump out the data for testing. However, since it has all been gathered back onto the master process, we only need to dump it on one process:
* Dump out data for verification
IF ( INUM .EQ.0 .AND. ROWS .LE. 20 ) THEN
FNAME = ’/tmp/mheatout’
OPEN(UNIT=9,NAME=FNAME,FORM=’formatted’)
DO C=1,COLS
WRITE(9,100)(BLACK(R,C),R=1,ROWS)
100 FORMAT(20F12.6)
ENDDO
CLOSE(UNIT=9)
ENDIF
CALL MPI_FINALIZE(IERR)
END
When this program executes with four processes, it produces the following output:
% mpif77 -c mheat.f
mheat.f:
MAIN mheat:
% mpif77 -o mheat mheat.o -lmpe
% mheat -np 4
Calling MPI_INIT
My Share 1 4 51 100
My Share 0 4 1 50
My Share 3 4 151 200
My Share 2 4 101 150
%
The ranks of the processes and the subsets of the computations for each process are shown in the output.
So that is a somewhat contrived example of the broadcast/gather approach to parallelizing an application. If the data structures are the right size and the amount of computation relative to communication is appropriate, this can be a very effective approach that may require the smallest number of code modifications compared to a single-processor version of the code.
MPI Summary
Whether you chose PVM or MPI depends on which library the vendor of your system prefers. Sometimes MPI is the better choice because it contains the newest features, such as support for hardware-supported multicast or broadcast, that can significantly improve the overall performance of a scatter-gather application.
A good text on MPI is Using MPI — Portable Parallel Programmingwith the Message-Passing Interface, by William Gropp, Ewing Lusk, and Anthony Skjellum (MIT Press). You may also want to retrieve and print the MPI specification from http://www.netlib.org/mpi/.
Closing Notes
In this chapter we have looked at the “assembly language” of parallel programming. While it can seem daunting to rethink your application, there are often some simple changes you can make to port your code to message passing. Depending on the application, a master-slave, broadcast-gather, or decomposed data approach might be most appropriate.
It’s important to realize that some applications just don’t decompose into message passing very well. You may be working with just such an application. Once you have some experience with message passing, it becomes easier to identify the critical points where data must be communicated between processes.
While HPF, PVM, and MPI are all mature and popular technologies, it’s not clear whether any of these technologies will be the long-term solution that we will use 10 years from now. One possibility is that we will use FORTRAN 90 (or FORTRAN 95) without any data layout directives or that the directives will be optional. Another interesting possibility is simply to keep using FORTRAN 77. As scalable, cache-coherent, non-uniform memory systems become more popular, they will evolve their own data allocation primitives. For example, the HP/Exemplar supports the following data storage attributes: shared, node-private, and thread-private. As dynamic data structures are allocated, they can be placed in any one of these classes. Node-private memory is shared across all the threads on a single node but not shared beyond those threads. Perhaps we will only have to declare the storage class of the data but not the data layout for these new machines.
PVM and MPI still need the capability of supporting a fault-tolerant style of computing that allows an application to complete as resources fail or otherwise become available. The amount of compute power that will be available to applications that can tolerate some unreliability in the resources will be very large. There have been a number of moderately successful attempts in this area such as Condor, but none have really caught on in the mainstream.
To run the most powerful computers in the world at their absolute maximum performance levels, the need to be portable is somewhat reduced. Making your particular application go ever faster and scale to ever higher numbers of processors is a fascinating activity. May the FLOPS be with you!
Footnotes
- Notice I said “not that much more effort.”
- Note: the exact compilation may be different on your system.
- One should not diminish the positive contributions of PVM, however. PVM was the first widely avail- able portable message-passing environment. PVM pioneered the idea of heterogeneous distributed computing with built-in format conversion.
- Sounds a little like HPF, no?
- Remember, each communicator may have a topology associated with it. A topology can be grid, graph, or none. Interestingly, the
MPI_COMM_WORLDcommunicator has no topology associated with it. - Note that you could do two time steps (one black-red-black iteration) if you exchanged two ghost columns at the top of the loop.


