4.4: Binary Relations

Binary relations define relations between two objects. For example, “less-than” on the real numbers relates every real number, \(a\), to a real number, \(b\), precisely when \(a < b\). Similarly, the subset relation relates a set, \(A\), to another set, \(B\), precisely when \(A \subseteq B\). A function \(f : A \rightarrow B\) is a special case of binary relation in which an element \(a \in A\) is related to an element \(b \in B\) precisely when \(b = f(a)\).

In this section we’ll define some basic vocabulary and properties of binary relations.

Definition \(\PageIndex{1}\)

A binary relation, \(R\), consists of a set, \(A\), called the domain of \(R\), a set, \(B\), called the codomain of \(R\), and a subset of \(A \times B\) called the graph of \(R\).

A relation whose domain is \(A\) and codomain is \(B\) is said to be “between \(A\) and \(B\)”, or “from \(A\) to \(B\).” As with functions, we write \(fR: A \rightarrow B\) to indicate that \(R\) is a relation from \(A\) to \(B\). When the domain and codomain are the same set, \(A\), we simply say the relation is “on \(A\).” It’s common to use “\(a\text{ }R\text{ }b\)” to mean that the pair \((a, b)\) is in the graph of \(R\). ⁵

Notice that Definition 4.4.1 is exactly the same as the definition in Section 4.3 of a function, except that it doesn’t require the functional condition that, for each domain element, \(a\), there is at most one pair in the graph whose first coordinate is \(a\). As we said, a function is a special case of a binary relation.

The “in-charge of” relation, Chrg, for MIT in Spring ’10 subjects and instructors is a handy example of a binary relation. Its domain, Fac, is the names of all the MIT faculty and instructional staff, and its codomain is the set, SubNums, of subject numbers in the Fall ’09–Spring ’10 MIT subject listing. The graph of Chrg contains precisely the pairs of the form

\[\nonumber (\langle \text{instructor-name} \rangle, \langle \text{subject-num} \rangle)\]

such that the faculty member named \(\langle \text{instructor-name} \rangle\) is in charge of the subject with number \(\langle \text{subject-num} \rangle)\) that was offered in Spring ’10. So graph(Chrg) contains pairs like

\[\label{4.4.1} \begin{array}[ccc]  & (\text{T}. & \text{Eng}, & 6.\text{UAT}) \\  (\text{G}. & \text{Freeman}, & 6.011)\\ (\text{G}. & \text{Freeman}, & 6.\text{UAT})\\ (\text{G}. & \text{Freeman}, & 6.881) \\ (\text{G}. & \text{Freeman}, & 6.882) \\ (\text{J}. & \text{Guttag}, & 6.00) \\ (\text{A}. & \text{R. Meyer}, & 6.042) \\ (\text{A}. & \text{R. Meyer}, & 18.062) \\ (\text{A}. & \text{R. Meyer}, & 6.844) \\ (\text{T}. & \text{Leighton}, & 6.042) \\ (\text{T}. & \text{Leighton}, & 18.062) \\ & \vdots & \end{array}\]

Some subjects in the codomain, SubNums, do not appear among this list of pairs—that is, they are not in range(Chrg). These are the Fall term-only subjects. Similarly, there are instructors in the domain, Fac, who do not appear in the list because they are not in charge of any Spring term subjects.

Relation Diagrams

Some standard properties of a relation can be visualized in terms of a diagram. The diagram for a binary relation, \(R\), has points corresponding to the elements of the domain appearing in one column (a very long column if domain\((R)\) is infinite). All the elements of the codomain appear in another column which we’ll usually picture as being to the right of the domain column. There is an arrow going from a point, \(a\), in the lefthand, domain column to a point, \(b\), in the righthand, codomain column, precisely when the corresponding elements are related by \(R\). For example, here are diagrams for two functions:

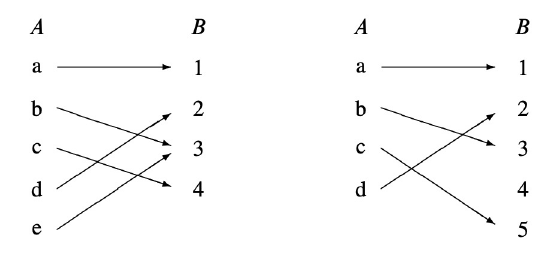
Being a function is certainly an important property of a binary relation. What it means is that every point in the domain column has at most one arrow coming out of it. So we can describe being a function as the “\(\leq 1\) arrow out” property. There are four more standard properties of relations that come up all the time. Here are all five properties defined in terms of arrows:

Definition \(\PageIndex{2}\)

A binary relation, \(R\), is:

• a function when it has the [\(\leq 1\) arrow out] property.
• surjective when it has the [\(\geq 1\) arrows in] property. That is, every point in the righthand, codomain column has at least one arrow pointing to it.
• total when it has the [\(\geq 1\) arrows out] property.
• injective when it has the [\(\leq 1\) arrow in] property.
• bijective when it has the [\(= 1\) arrow out] and the [\(= 1\) arrow in] property.

From here on, we’ll stop mentioning the arrows in these properties and for example, just write [\(\leq 1\) in] instead of [\(\leq 1\) arrows in].

So in the diagrams above, the relation on the left has the [= 1 out] and [\(\geq 1\) in] properties, which means it is a total, surjective function. But it does not have the [\(\leq 1\) in] property because element 3 has two arrows going into it; it is not injective.

The relation on the right has the [= 1 out] and [\(\leq 1\) in] properties, which means it is a total, injective function. But it does not have the [\(\geq 1\) in] property because element 4 has no arrow going into it; it is not surjective.

The arrows in a diagram for \(R\) correspond, of course, exactly to the pairs in the graph of \(R\). Notice that the arrows alone are not enough to determine, for example, if \(R\) has the [\(\geq 1\) out], total, property. If all we knew were the arrows, we wouldn’t know about any points in the domain column that had no arrows out. In other words, graph(\(R\)) alone does not determine whether \(R\) is total: we also need to know what domain(\(R\)) is.

Example \(\PageIndex{3}\)

The function defined by the formula \(1/x^2\) has the [\(\geq 1\) out] property if its domain is \(\mathbb{R}^+\), but not if its domain is some set of real numbers including 0. It has the [= 1 in] and [= 1 out] property if its domain and codomain are both \(\mathbb{R}^+\), but it has neither the [\(\leq 1\) in] nor the [\(\geq 1\) out] property if its domain and codomain are both \(\mathbb{R}\).

Relational Images

The idea of the image of a set under a function extends directly to relations.

Definition \(\PageIndex{4}\)

The image of a set, \(Y\), under a relation, \(R\), written \(R(Y)\), is the set of elements of the codomain, \(B\), of \(R\) that are related to some element in \(Y\). In terms of the relation diagram, \(R(Y)\) is the set of points with an arrow coming in that starts from some point in \(Y\).

For example, the set of subject numbers that Meyer is in charge of in Spring ’10 is exactly Chrg(A. Meyer). To figure out what this is, we look for all the arrows in the Chrg diagram that start at “A. Meyer,” and see which subject-numbers are at the other end of these arrows. Looking at the list (4.4) of pairs in graph(Chrg), we see that these subject-numbers are {6.042, 18.062, 6.844}. Similarly, to find the subject numbers that either Freeman or Eng are in charge of, we can collect all the arrows that start at either “G. Freeman,” or “T. Eng” and, again, see which subjectnumbers are at the other end of these arrows. This is Chrg ({G. Freeman, T. Eng}). Looking again at the list (4.4), we see that

Chrg ({G. Freeman, T. Engg}) = {6.011, 6.881, 6.882, 6.UAT}

Finally, Fac is the set of all in-charge instructors, so Chrg(Fac) is the set of all the subjects listed for Spring ’10.

Inverse Relations and Images

Definition \(\PageIndex{5}\)

The inverse, \(R^{-1}\) of a relation \(R : A \rightarrow B\) is the relation from \(B\) to \(A\) defined by the rule

\[\nonumber b R^{-1} a \text{ IFF } a R b\]

In other words, \(R^{-1}\) is the relation you get by reversing the direction of the arrows in the diagram of \(R\).

Definition \(\PageIndex{6}\)

The image of a set under the relation, \(R^{-1}\), is called the inverse image of the set. That is, the inverse image of a set, \(X\), under the relation, \(R\), is defined to be \(R^{-1}(X)\).

Continuing with the in-charge example above, the set of instructors in charge of 6.UAT in Spring ’10 is exactly the inverse image of {6.UAT} under the Chrg relation. From the list (\ref{4.4.1}), we see that Eng and Freeman are both in charge of 6.UAT, that is,

{T. Eng, D. Freeman} \(\subseteq \textit{Chrg}^{-1}\)({6.UAT}).

We can’t assert equality here because there may be additional pairs further down the list showing that additional instructors are co-incharge of 6.UAT.

Now let Intro be the set of introductory course 6 subject numbers. These are the subject numbers that start with “6.0.” So the set of names of the instructors who were in-charge of introductory course 6 subjects in Spring ’10, is \(\textit{Chrg}^{-1}\)(Intro). From the part of the Chrg list shown in (\ref{4.4.1}), we see that Meyer, Leighton, Freeman, and Guttag were among the instructors in charge of introductory subjects in Spring ’10. That is,

{Meyer, Leighton, Freeman, Guttag} \(\subseteq \textit{Chrg}^{-1}\)(Intro).

Finally, \(\textit{Chrg}^{-1}\)(SubNums), is the set of all instructors who were in charge of a subject listed for Spring ’10.

 

⁵Writing the relation or operator symbol between its arguments is called infix notation. Infix expressions like “\(m < n\)” or “\(m + n\)” are the usual notation used for things like the less-then relation or the addition operation rather than prefix notation like “\(<(m, n)\)” or “\(+(m, n)\).”