11.1: Vertex Adjacency and Degrees

Simple graphs are defined as digraphs in which edges are undirected—they connect two vertices without pointing in either direction between the vertices. So instead of a directed edge \(\langle v \rightarrow w \rangle\) which starts at vertex \(v\) and ends at vertex \(w\), a simple graph only has an undirected edge, \(\langle v \rightarrow w \rangle\), that connects \(v\) and \(w\).

Definition \(\PageIndex{1}\)

A simple graph, \(G\), consists of a nonempty set, \(V(G)\), called the vertices of \(G\), and a set \(E(G)\) called the edges of \(G\). An element of \(V(G)\) is called a vertex. A vertex is also called a node; the words “vertex” and “node” are used interchangeably. An element of \(E(G)\) is an undirected edge or simply an “edge.” An undirected edge has two vertices \(u \neq v\) called its endpoints. Such an edge can be represented by the two element set \(\{u,v\}\). The notation \(\langle u \rightarrow v \rangle\) denotes this edge.

Both \(\langle u \rightarrow v \rangle\) and \(\langle v \rightarrow u \rangle\) define the same undirected edge, whose endpoints are \(u\) and \(v\).

Figure 11.1 An example of a graph with 9 nodes and 8 edges.

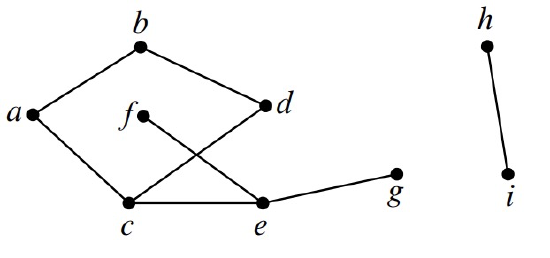
For example, let \(H\) be the graph pictured in Figure 11.1. The vertices of \(H\) correspond to the nine dots in Figure 11.1, that is,

\[\nonumber V(H) = \{a, b, c, d, e, f, g, h, i\}.\]

The edges correspond to the eight lines, that is,

\[\nonumber E(H) = \{ \langle a \rightarrow b \rangle, \langle a \rightarrow c \rangle, \langle b \rightarrow d \rangle, \langle c \rightarrow d \rangle, \langle c \rightarrow e \rangle, \langle e \rightarrow f \rangle, \langle e \rightarrow g \rangle, \langle h \rightarrow i \rangle \}.\]

Mathematically, that’s all there is to the graph \(H\).

Definition: \(\PageIndex{2}\)

Two vertices in a simple graph are said to be adjacent iff they are the endpoints of the same edge, and an edge is said to be incident to each of its endpoints. The number of edges incident to a vertex \(v\) is called the degree of the vertex and is denoted by \(\text{deg}(v)\). Equivalently, the degree of a vertex is the number of vertices adjacent to it.

For example, for the graph \(H\) of Figure 11.1, vertex \(a\) is adjacent to vertex \(b\), and \(b\) is adjacent to \(d\). The edge \(\langle a \rightarrow c \rangle\) is incident to its endpoints \(a\) and \(c\). Vertex \(h\) has degree 1, \(d\) has degree 2, and \(\text{deg}(e) = 3\). It is possible for a vertex to have degree 0, in which case it is not adjacent to any other vertices. A simple graph, \(G\), does not need to have any edges at all. \(|E(G)|\) could be zero, implying that the degree of every vertex would also be zero. But a simple graph must have at least one vertex—\(|V(G)|\) is required to be at least one.

An edge whose endpoints are the same is called a self-loop. Self-loops aren’t allowed in simple graphs.¹ In a more general class of graphs called multigraphs, there can be more than one edge with the same two endpoints, but this doesn’t happen in simple graphs, because every edge is uniquely determined by its two endpoints. Sometimes graphs with no vertices, with self-loops, or with more than one edge between the same two vertices are convenient to have, but we don’t need them, and sticking with simple graphs is simpler.

For the rest of this chapter we’ll use “graphs” as an abbreviation for “simple graphs.”

A synonym for “vertices” is “nodes,” and we’ll use these words interchangeably. Simple graphs are sometimes called networks, edges are sometimes called arcs. We mention this as a “heads up” in case you look at other graph theory literature; we won’t use these words.

¹You might try to represent a self-loop going between a vertex \(v\) and itself as \(\{v, v\}\), but this equals \(\{v\}\). It wouldn’t be an edge, which is defined to be a set of two vertices.