17.3: The Four-Step Method for Conditional Probability

Last updated
Save as PDF

Page ID: 48424

Eric Lehman, F. Thomson Leighton, & Alberty R. Meyer
Google and Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

In a best-of-three tournament, the local C-league hockey team wins the first game with probability \(1/2\). In subsequent games, their probability of winning is determined by the outcome of the previous game. If the local team won the previous game, then they are invigorated by victory and win the current game with probability \(2/3\). If they lost the previous game, then they are demoralized by defeat and win the current game with probability only \(1/3\). What is the probability that the local team wins the tournament, given that they win the first game?

This is a question about a conditional probability. Let \(A\) be the event that the local team wins the tournament, and let \(B\) be the event that they win the first game. Our goal is then to determine the conditional probability \(\text{Pr}[A \mid B]\).

We can tackle conditional probability questions just like ordinary probability problems: using a tree diagram and the four step method. A complete tree diagram is shown in Figure 17.1.

Figure 17.1 The tree diagram for computing the probability that the local team wins two out of three games given that they won the first game.

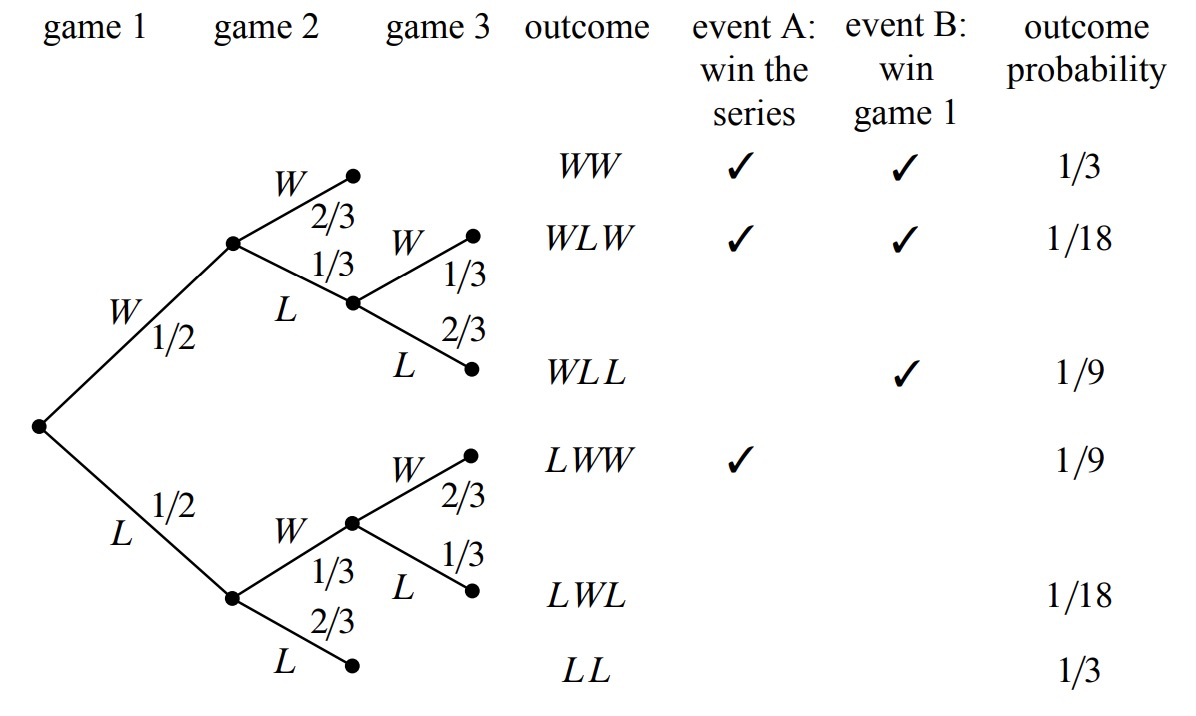
Step 1: Find the Sample Space

Each internal vertex in the tree diagram has two children, one corresponding to a win for the local team (labeled \(W\)) and one corresponding to a loss (labeled \(L\)). The complete sample space is:

\[\nonumber S = \{WW, WLW, WLL, LWW, LWL, LL\}.\]

Step 2: Define Events of Interest

The event that the local team wins the whole tournament is:

\[\nonumber T = \{WW, WLW, LWW\}.\]

And the event that the local team wins the first game is:

\[\nonumber F = \{WW, WLW, WLL\}.\]

The outcomes in these events are indicated with check marks in the tree diagram in Figure 17.1.

Step 3: Determine Outcome Probabilities

Next, we must assign a probability to each outcome. We begin by labeling edges as specified in the problem statement. Specifically, the local team has a \(1/2\) chance of winning the first game, so the two edges leaving the root are each assigned probability \(1/2\). Other edges are labeled \(1/3\) or \(2/3\) based on the outcome of the preceding game. We then find the probability of each outcome by multiplying all probabilities along the corresponding root-to-leaf path. For example, the probability of outcome \(WLL\) is:

\[\nonumber \frac{1}{2} \cdot \frac{1}{3} \cdot \frac{2}{3} = \frac{1}{9}.\]

Step 4: Compute Event Probabilities

We can now compute the probability that the local team wins the tournament, given that they win the first game:

\[\begin{aligned} \text{Pr}[A \mid B] &= \dfrac{\text{Pr}[A \cap B]}{\text{Pr}[B]} \\ &= \dfrac{\text{Pr}[\{WW, WLW\}]}{\text{Pr}[\{WW,WLW,WLL\}]} \\ &= \dfrac{1/3 + 1/18}{1/3 + 1/18 + 1/9} \\ &= \dfrac{7}{9}. \end{aligned}\]

We’re done! If the local team wins the first game, then they win the whole tournament with probability \(7/9\).