8.2: Acceptance Angle
- Page ID
- 19595
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section, we consider the problem of injecting light into a fiber optic cable. The problem is illustrated in Figure \(\PageIndex{1}\).
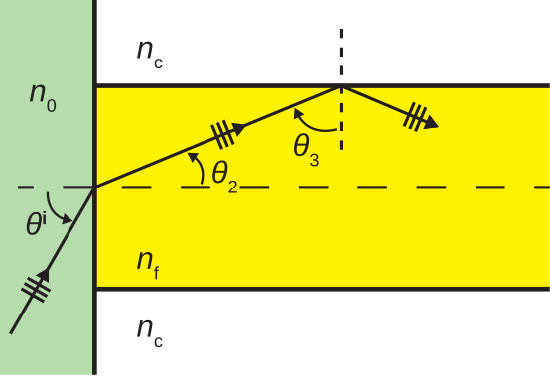
In this figure, we see light incident from a medium having index of refraction \(n_0\), with angle of incidence \(\theta^i\). The light is transmitted with angle of transmission \(\theta_2\) into the fiber, and is subsequently incident on the surface of the cladding with angle of incidence \(\theta_3\). For light to propagate without loss within the cable, it is required that
\[\sin\theta_3 \ge \frac{n_c}{n_f} \label{m0192_eCAnm} \]
since this criterion must be met in order for total internal reflection to occur.
Now consider the constraint that Equation \ref{m0192_eCAnm} imposes on \(\theta^i\). First, we note that \(\theta_3\) is related to \(\theta_2\) as follows:
\[\theta_3 = \frac{\pi}{2} - \theta_2 \nonumber \]
therefore
\begin{align} \sin\theta_3 &= \sin\left(\frac{\pi}{2} - \theta_2\right) \\ &= \cos\theta_2 \end{align}
so
\[\cos\theta_2 \ge \frac{n_c}{n_f} \nonumber \]
Squaring both sides, we find:
\[\cos^2\theta_2 \ge \frac{n_c^2}{n_f^2} \nonumber \]
Now invoking a trigonometric identity:
\[1-\sin^2\theta_2 \ge \frac{n_c^2}{n_f^2} \nonumber \]
so:
\[\sin^2\theta_2 \le 1-\frac{n_c^2}{n_f^2} \label{m0192_e1} \]
Now we relate the \(\theta_2\) to \(\theta^i\) using Snell’s law:
\[\sin\theta_2 = \frac{n_0}{n_f}\sin\theta^i \nonumber \]
so Equation \ref{m0192_e1} may be written:
\[\frac{n_0^2}{n_f^2}\sin^2\theta^i \le 1-\frac{n_c^2}{n_f^2} \nonumber \]
Now solving for \(\sin\theta^i\), we obtain:
\[\sin\theta^i \le \frac{1}{n_0}\sqrt{ n_f^2 - n_c^2 } \nonumber \]
This result indicates the range of angles of incidence which result in total internal reflection within the fiber. The maximum value of \(\theta^i\) which satisfies this condition is known as the acceptance angle \(\theta_a\), so:
\[\theta_a \triangleq \arcsin\left(\frac{1}{n_0}\sqrt{ n_f^2 - n_c^2 }\right) \nonumber \]
This leads to the following insight:
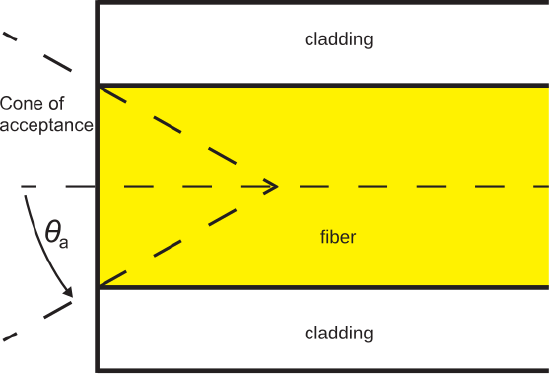
In order to effectively launch light in the fiber, it is necessary for the light to arrive from within a cone having half-angle \(\theta_a\) with respect to the axis of the fiber.
The associated cone of acceptance is illustrated in Figure \(\PageIndex{2}\).
It is also common to define the quantity numerical aperture NA as follows:
\[\mbox{NA} \triangleq \frac{1}{n_0}\sqrt{ n_f^2 - n_c^2 } \label{m0192_eNA} \]
Note that \(n_0\) is typically very close to \(1\) (corresponding to incidence from air), so it is common to see NA defined as simply \(\sqrt{ n_f^2 - n_c^2 }\). This parameter is commonly used in lieu of the acceptance angle in datasheets for fiber optic cable.
Typical values of \(n_f\) and \(n_c\) for an optical fiber are 1.52 and 1.49, respectively. What are the numerical aperture and the acceptance angle?
Solution
Using Equation \ref{m0192_eNA} and presuming \(n_0=1\), we find NA \(\cong \underline{0.30}\). Since \(\sin\theta_a =\) NA, we find \(\theta_a=\underline{17.5^{\circ}}\). Light must arrive from within \(17.5^{\circ}\) from the axis of the fiber in order to ensure total internal reflection within the fiber.


