1.5: Properties of Materials

Macroscopic Properties

To understand energy conversion devices, we need to understand materials both microscopically on the atomic scale and macroscopically on large scales. A macroscopic property is a property that applies to large pieces of the material as opposed to microscopic sized pieces.

One way to classify materials is based on their state of matter. Materials can be classified as solids, liquids, gases, or plasmas. A plasma is an ionized gas. Other more unusual states of matter exist such as Bose Einstein condensates, but they will not be discussed in this book.

Figure \(\PageIndex{1}\): Illustration of crystalline, amorphous, and polycrystalline atomic structure.

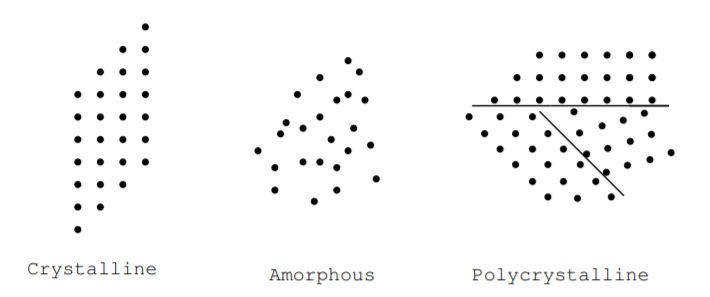
We can further classify solids as crystalline, polycrystalline, or amorphous based on the regularity of their atomic structure [9]. Figure \(\PageIndex{1}\) illustrates these terms. In a crystal, the arrangement of atoms is periodic. The atoms may be arranged in a cubic array, hexagonal array, or some other way, but they are arranged periodically in three dimensions. In an amorphous material, the arrangement of the atoms is not periodic. The term amorphous means glassy. A polycrystalline material is composed of small crystalline regions. These definitions can apply to materials made of single elements or materials made of multiple elements. Many energy conversion devices are made from very pure crystalline, amorphous, or polycrystalline materials. For example, amorphous cadmium telluride is used to make solar cells, and crystalline silicon is used to make Hall effect devices. Many materials, including both silicon and silicon dioxide, can be found in all three of these forms at room temperature. In crystalline and amorphous silicon, for example, the silicon atoms may have the same number of nearest neighbors, and the density of atoms in both materials may be the same, but there is no medium-range order in the amorphous material. Electrical properties of crystalline, amorphous, and polycrystalline forms of a material may differ. Electrons can flow more easily through a pure crystalline material while electrons are more likely to be scattered or absorbed as they flow through an amorphous material, crystalline materials with impurities, or a crystalline material with crystal defects.

We can further classify crystals as either isotropic or anisotropic [10, p. 210]. A crystal is isotropic if its macroscopic structure and material properties are the same in each direction. A crystal is anisotropic if the macroscopic structure and material properties are different in different directions.

We can also classify materials based on how they behave when a voltage is applied across the material [11]. In a conductor, electrons flow easily in the presence of an applied voltage or electric field. In an insulator, also called a dielectric, electrons do not flow in the presence of an applied voltage or electric field. In the presence of a small external voltage or electric field, a semiconductor acts as an insulator, and in the presence of a strong voltage or electric field, a semiconductor acts as a conductor. Both solids and liquids can be conductors, and both solids and liquids can be insulators. For example, copper is a solid conductor while salt water is a liquid conductor.

Microscopic Properties

The electron configuration lists the energy levels occupied by electrons around an atom. The electron configuration can describe neutral or ionized atoms, and it can describe atoms in the lowest energy state or excited atoms. For example, the electron configuration of a neutral aluminum atom in the lowest energy state is \(1s^{2}2s^{2}2p^{6}3s^{2}3p^{1}\). The electron configuration of an aluminum Al\(^{+}\) ion in the lowest energy state is \(1s^{2}2s^{2}2p^{6}3s^{2}\), and the electron configuration of a neutral aluminum atom with an excited electron can be written as \(1s^{2}2s^{2}2p^{6}3s^{2}4s^{1}\).

Electrons are labeled by four quantum numbers: the principle quantum number, the azimuthal quantum number, the magnetic quantum number, and the spin quantum number [6] [12]. No two electrons around an atom can have the same set of quantum numbers. The principle quantum number takes integer values, 1, 2, 3 and so on. All electrons with the same principle quantum number are said to be in the same shell. The large numbers in the electron configuration refer to principle quantum numbers. The neutral aluminum atom in the lowest energy state has two electrons in the 1 shell, eight electrons in the 2 shell, and three electrons in the 3 shell. For most atoms, especially atoms with few electrons, electrons with lower principle quantum numbers both are spatially closer to the nucleus and require the most energy to remove. However, there are exceptions to this idea for some electrons around larger atoms [13] [14].

Azimuthal quantum numbers are integers, and these values define subshells. For shells with principle quantum number \(\mathfrak{n}\), the azimuthal quantum number can take values from 0 to \(\mathfrak{n}-1\). In the electron configuration, values of this quantum number are denoted by lowercase letters: \(s =0\), \(p =1\), \(d =2\), \(f =3\), and so on. Magnetic quantum numbers are also integers, and these values define orbitals. For a subshell with azimuthal quantum number \(l\), the magnetic quantum number takes values from \(-l\) to \(l\). In the electron configuration, superscript numbers indicate the magnetic quantum number. Spin quantum numbers of electrons can take the values \(\frac{1}{2}\) and \(\frac{-1}{2}\). They are not explicitly denoted in the electron configuration.

Consider again the neutral aluminum atom in the lowest energy state. This atom has electrons with principle quantum numbers \(\mathfrak{n}\) = 1, 2, and 3. For electrons with principle quantum number 1, the only possible values for both the azimuthal quantum number and the magnetic quantum number are zero. The spin quantum number can take the values of \(\frac{1}{2}\) and \(\frac{-1}{2}\). Only two electrons can occupy the 1 shell, and these electrons are denoted by the \(1s^{2}\) term of the electron configuration. For the electrons with principle quantum number 2, the azimuthal quantum number can be 0 or 1. Two electrons can occupy the \(2s\) orbital, and six electrons can occupy the \(2p\) orbital. For the 3 shell, the azimuthal quantum number can take three possible values: \(s =0\), \(p =1\), and \(d =2\). However since aluminum only has 13 electrons, electrons do not have all of these possible values, so the 3 shell is only partially filled. The atoms in the rightmost column of the periodic table have completely filled shells. They are rarely involved in chemical reactions because adding electrons, removing electrons, or forming chemical bonds would require too much energy.

Valence electrons are the electrons that are most easily ripped off an atom. Valence electrons are the electrons involved in chemical reactions, and electrical current is the flow of valence electrons. Other, inner shell, electrons may be involved in chemical reactions or electrical current only in cases of unusually large applied energies, and these situations will not be discussed in this text. Valence electrons occupy the subshell or subshells with the highest quantum numbers, and valence electrons are not part of completely filled shells. For the example of the neutral aluminum atom in the lowest energy state, the three electrons in the 3 shell are valence electrons.

Where are the electrons around the atom spatially? This question is of interest to chemists, physicists, and electrical engineers. If we know the orbital of an electron, we have some information on where the electron is likely to be found spatially around an atom. However, identifying the location of an electron with any degree of precision is difficult for multiple reasons. First, atoms are tiny, roughly \(10^{-10}\) m in diameter. Second, at any temperature above absolute zero, atoms and electrons are continually in motion. Third, electrons have both particle-like and wave-like properties. Fourth, according to Heisenberg's Uncertainty Principle, the position and momentum of an electron cannot simultaneously be known with complete precision. At best, you can say that an electron is most likely in some region and moves with some range of speed. Fifth, in many materials including conductors and semiconductors, valence electrons are shared by many atoms instead of bound to an individual atom [10, p. 544].