1.6: Electromagnetic Waves

Maxwell's Equations

In this text, $V$ and $I$ denote DC voltage and current respectively while $v$ and $i$ denote AC or time varying voltage and current. In circuit analysis, we are unconcerned with what happens outside these wires. We are only interested in node voltages and currents through wires. Furthermore, the voltages and currents in the circuit are described as functions of time $t$ but not position $(x, y, z)$. Devices like resistors, capacitors, and inductors too are assumed to be point-like and not extended with respect to position $(x, y, z)$. This set of assumptions is just a model. In reality, if two nodes in a circuit have a voltage difference between them, then necessarily a force is exerted on nearby charges not in the path of the circuit. This force per unit charge is the electric field intensity $\overrightarrow{E}$. Similarly, if there is current flowing through a wire, there is necessarily a force exerted on electrons in nearby loops of wire, and this force per unit current element is the magnetic flux density $\overrightarrow{B}$. Energy can be stored in an electric or magnetic field. In later chapters, we will discuss devices, including antennas, electro-optic devices, photovoltaic devices, lamps, and lasers, that convert energy of an electromagnetic field to or from electricity. Four interrelated vector quantities are used to describe electromagnetic fields. These vector fields are functions of position $(x, y, z)$ and time $t$. The four vector fields are

• $\overrightarrow{E}(x, y, z, t) =$ Electric field intensity in $\frac{V}{m}$
• $\overrightarrow{D}(x, y, z, t) =$ Displacement field density in $\frac{C}{m^2}$
• $\overrightarrow{H}(x, y, z, t) =$ Magnetic field intensity in $\frac{A}{m}$
• $\overrightarrow{B}(x, y, z, t) =$ Magnetic flux density in $\frac{Wb}{m^2}$

In these expressions, $V$ represents the units volts, $C$ represents the units coulombs, $A$ represents the units amperes, and $Wb$ represents the units webers. Additional abbreviations for units are listed in Appendix B.

Coulomb's law:

$$\overrightarrow{F} = \frac{Q_1 Q_2 \hat a_r}{4 \pi \epsilon r^{2}} \nonumber$$

tells us that charged objects exert forces on other charged objects. In this expression, $Q_1$ and $Q_2$ are the magnitude of the charges in coulombs. The quantity $\epsilon$ is the permittivity of the surrounding material in units farads per meter, and it is discussed further in 1.6.3 and 2.1.3. The quantity $r$ is the distance between the charges in meters, and $\hat a_r$ is a unit vector pointing along the direction between the charges. Force in newtons is represented by $\overrightarrow{F}$. Opposite charges attract, and like charges repel. Electric field intensity is force per unit charge, so the electric field intensity due to a point charge is given by $$\overrightarrow{E} = \frac{Q \hat a_r}{4 \pi \epsilon r^{2}} \nonumber$$

These vector fields can describe forces on charges or currents in a circuit as well as outside the path of a circuit. Maxwell's equations relate time varying electric and magnetic fields. Maxwell's equations in differential form are:

$$\overrightarrow{\nabla} \times \overrightarrow{E} = -\frac{\partial \overrightarrow{B}}{\partial t} \quad \text{Faraday's Law} \nonumber$$

$$\overrightarrow{\nabla} \times \overrightarrow{H} = \overrightarrow{J} + \frac{\partial \overrightarrow{D}}{\partial t} \quad \text{Ampere's Law} \nonumber$$

$$\overrightarrow{\nabla} \cdot \overrightarrow{D} = \rho_{ch} \quad \text{Gauss's Law for the Electric Field} \nonumber$$

$$\overrightarrow{\nabla} \cdot \overrightarrow{B} = 0 \quad \text{Gauss's Law for the Magnetic Field} \nonumber$$

The additional quantities in Maxwell's equations are the volume current density $\overrightarrow{J}$ in $\frac{A}{m^2}$ and the charge density $\rho_{ch}$ in $\frac{C}{m^3}$. In this text, we will not be solving Maxwell's equations, but we will encounter references to them.

The quantity $\overrightarrow{\nabla}$ is called the del operator. In Cartesian coordinates, it is given by

$$\overrightarrow{\nabla} =\hat a_x \frac{\partial}{\partial x} + \hat a_y \frac{\partial}{\partial y} + \hat a_z \frac{\partial}{\partial z}. \nonumber$$

When this operator acts on a scalar function, $\overrightarrow{\nabla}f$, it is called the gradient. The gradient of a scalar function returns a vector representing the spatial derivative of the function, and it points in the direction of largest change in that function. In Maxwell's equations, $\overrightarrow{\nabla}$ acts on vector, instead of scalar, functions. The operation $\overrightarrow{\nabla} \times \overrightarrow{E}$ is called the curl, and the operation $\overrightarrow{\nabla} \cdot \overrightarrow{E}$ is called the divergence. Both of these operations represent types of spatial derivatives of vector functions. The del operator obeys the identity

$$\nabla^2 =\overrightarrow{\nabla} \cdot \overrightarrow{\nabla}. \nonumber$$

The operation $\nabla^2f$ is called the Laplacian of a scalar function, and it represents the spatial second derivative of that function.

Electromagnetic Waves in Free Space

Electromagnetic waves travel through empty space at the speed of light in free space, $c = 2.998 \cdot 10^8 \frac{m}{s}$, and through other materials at speeds less than $c$. For a sinusoidal electromagnetic wave, the speed of propagation is the product of the frequency and wavelength $$|\overrightarrow{v}| =f \lambda \nonumber$$

where $|\overrightarrow{v}|$ is the magnitude of the velocity in $\frac{m}{s}$, $f$ is the frequency in Hz, and $\lambda$ is the wavelength in meters. In free space, this becomes $$c =f \lambda. \nonumber$$

The speed of light in free space is related to two constants which describe free space. $$c = \frac{1}{\sqrt{\epsilon_0\mu_0}} \nonumber$$

The permittivity of free space is given by $\epsilon_0 = 8.854 \cdot 10^{-12} \frac{F}{m}$ where $F$ represents farads, and the permeability of free space is given by $\mu_0 = 1.257 \cdot 10^{-6} \frac{H}{m}$ where $H$ represents henries. (Constants specified in this section and in Appendix A are rounded to four significant digits.)

In free space, the electric field intensity $\overrightarrow{E}$ and the displacement flux density $\overrightarrow{D}$ are related by $\epsilon_0$. $$\overrightarrow{D} = \mu_0 \overrightarrow{E} \nonumber$$

Relatedly in free space, the magnetic field intensity $\overrightarrow{H}$ and the magnetic flux density $\overrightarrow{B}$ are related by $mu_0$. $$\overrightarrow{B} = \mu_0 \overrightarrow{H}. \nonumber$$

Electromagnetic Waves in Materials

Electromagnetic fields interact very differently with conductors and with insulators. Electromagnetic fields do not propagate into perfect conductors. Instead, charges and currents accumulate on the surface. While no materials are perfect conductors, commonly encountered metals like copper and aluminum are very good conductors. When these materials are placed in an external electromagnetic field, surface charges and currents build up, and the electromagnetic field in the material quickly approaches zero. Electromagnetic fields propagate through perfect insulators for long distances without decaying, and no charges or currents can accumulate on the surface because there are no electrons free from their atoms. In practical dielectrics, electromagnetic waves propagate long distances with very little attenuation. For example, optical electromagnetic waves remain strong enough to detect after propagating hundreds of kilometers through optical fibers made of pure silicon dioxide [10, p. 886].

Resistance $R$ in ohms, capacitance $C$ in farads, and inductance $L$ in henries describe the electrical properties of devices. Resistivity $\rho$ in $\Omega m$, permittivity $\epsilon$ in $\frac {F}{m}$, and permeability $\mu$ in $\frac{H}{m}$ describe the electrical properties of materials. The quantities $\rho$, $\epsilon$, and $\mu$ describe properties of materials alone while the quantities $R$, $C$, and $L$ incorporate effects the material, shape, and size of a device.

Resistivity $\rho$ is a measure of the inability of charges or electromagnetic waves to propagate through a material. Conductors have a very small resistivity while insulators have a large resistivity. Sometimes electrical conductivity, $\sigma =\frac{1}{\rho}$ in units $\frac{1}{\Omega m}$, is used in place of the resistivity. For a device made of a uniform material with length $l$ and cross sectional area $A$, resistance and resistivity are related by $$R =\frac{\rho l}{A}. \nonumber$$

Resistance is a measure of the inability of charges or electromagnetic waves to flow through a device while resistivity is a measure of the inability to flow through a material.

Figure $\PageIndex{1}$: Geometry of a parallel plate capacitor and partial turn inductor.

Permeability $\mu$ is a measure of the ability of a material to store energy in the magnetic field due to currents distributed throughout the material. Materials can also be described by their relative permeability $\mu_r$, a unitless measure. $$\mu_r = \frac{\mu}{\mu_0} \nonumber$$

While permeability describes a material, inductance describes a device. The magnetic flux density in a material is a scaled version of the magnetic field intensity.

$$\overrightarrow{B} =\mu\overrightarrow{H} \nonumber$$

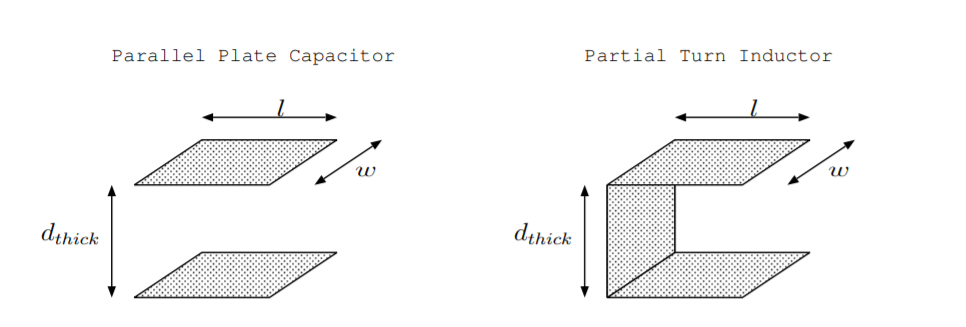
Often insulators have permeabilities close to $mu_0$ while conductors used to make permanent magnets have significantly larger permeabilities. The right part of Figure $\PageIndex{1}$: shows a partial turn coil in a vacuum with length $l$, thickness $d_{thick}$, and width $w$. The inductance and permeability of this device are related by [11, p. 311]

$$L =\frac{\mu d_{thick} l}{w}. \nonumber$$

Permittivity $\epsilon$ is a measure of the ability of a material to store energy as an electric field due to charge separation distributed throughout the material. Materials can also be described by their relative permittivity $\epsilon_r$, a unitless measure. $$\epsilon_r =\frac{\epsilon}{\epsilon_0} \nonumber$$

The displacement flux density in a material is a scaled version of the electric field intensity. $$\overrightarrow{D} =\epsilon\overrightarrow{E} \nonumber$$

Some insulators have a permittivity hundreds of times larger than the permittivity of free space. Permittivity is a measure of ability to store energy in a material while capacitance is a measure of the ability to store energy in in a device.

A uniform parallel plate capacitor with cross sectional area of plates $A =l \cdot w$ and distance between plates $d_{thick}$, is shown on the left part of Figure $\PageIndex{1}$, and it has capacitance $$C =\frac{\epsilon A}{d_{thick}} \nonumber$$ where $\epsilon$ is the permittivity of the insulator between the plates.

Permittivity, permeability, and resistivity, depend on frequency. In some contexts, the frequency dependence can be ignored, and throughout most of this text, these quantities will be assumed to be constants. In other contexts, the frequency dependence can be quite significant. For example, the permittivity of semiconductor materials is a strong function of frequency for frequencies close to the semiconductor energy gap. The permittivity $\epsilon(\omega)$ and resistivity $\rho(\omega)$ are not independent. If one of them is known as a function of frequency and $\mu$ is assumed constant, the other can be derived. This relationship is known as the Kramers Kronig relationship [10] or occasionally as the dielectric dispersion formula [15].

When discussing electrical properties of a device, resistance, inductance, and capacitance are combined into one complex measure, the impedance. Similarly, some authors find it convenient to combine resistivity, permittivity, and permeability into a pair of complex measures of the electrical properties of materials [6]. The complex permittivity is defined $\epsilon^* =\epsilon+j\rho$, and the complex permeability is defined $\mu^* =\mu+j\rho_{mag}$. The quantity $\rho$ represents the resistivity which is a measure of the energy converted to heat as a charge flows through a material due to an applied electrical field. The quantity $\rho_{mag}$ represents an analogous measure of energy converted to heat from currents in an applied magnetic field. Complex permittivity and permeability will not be used in this text.