2.4: Problems

2.1. A parallel plate capacitor has a capacitance of \(C =10 pF\). The plates have area \(0.025 cm^2\). A dielectric layer of thickness \(d_{thick} = 0.01 mm\) separates the plates. For the dielectric layer, calculate the permittivity \(\epsilon\), the relative permittivity \(\epsilon_r\), and the electric susceptibility \(\chi_e\).

2.2. We often assume that the capacitance of a capacitor and the permittivity of a material are constants. However, sometimes these quantities are better described as functions of frequency. Consider a capacitor made from parallel plates of area \(0.025 cm^2\) separated by \(0.01 mm\). Assume that for \(\omega \lesssim 10^6 \frac{rad}{s}\), the capacitance is well modeled by \[C(\omega) = 8 \cdot 10^{-11} + 3 \cdot 10^{-15} \omega \nonumber \] in farads. For the dielectric material between the plates of the capacitor, calculate the permittivity \(\epsilon(\omega)\), the relative permittivity \(\epsilon_r(\omega)\), and the electric susceptibility \(\chi_e(\omega)\).

2.3. A cylindrical sandwich cookie has a radius of 0.75 in. The cookie is made from two wafers, each of thickness 0.15 in, which are perfect dielectrics of relative permittivity \(\epsilon_r =2.8\). Between the wafers is a layer of cream filling of thickness 0.1 in which is a perfect dielectric of relative permittivity \(\epsilon_r =2.2\). Find the overall capacitance of the cookie. Hint: Capacitances in series combine as \(\frac{1}{\frac{1}{C_1}+\frac{1}{C_2}}\).

2.4. A parallel plate capacitor has a capacitance of \(3 \mu F\).

(a) Suppose another capacitor is made using the same dielectric material and with the same cross sectional area. However, the thickness of the dielectric between the plates of the capacitor is double that of the original capacitor. What is its capacitance?

(b) Suppose a third capacitor is made with the same cross sectional area and thickness as the first capacitor, but from a material with twice the permittivity. What is its capacitance?

2.5. A piezoelectric material has a permittivity of \(\epsilon = 3.54 \cdot 10^{-11} \frac{F}{m}\) and has a piezoelectric strain constant of \(d =2 \cdot 10^{-10} \frac{m}{V}\). If the material is placed in an electric field of strength \(|\overrightarrow{E}| =70 \frac{V}{m}\) and is subjected to a stress of \(|\overrightarrow{\varsigma}| =3.5 \frac{N}{m^2}\). Calculate the material polarization.

2.6. A piezoelectric material has permittivity \(\epsilon_r = 2.5\). If the material is placed in an electric field of strength \(|\overrightarrow{E}| =2\cdot10^3\frac{V}{m}\) and is subjected to a stress of \(|\overrightarrow{\varsigma}| =200 \frac{N}{m^2}\), the material polarization of the material is \(3.2 \cdot 10^{-8} \frac{C}{m^2}\). Calculate \(d\), the piezoelectric strain constant.

2.7. Consider two piezoelectric devices of the same size and shape. The dielectric material of the first device has a permittivity of \(\epsilon = 2.21 \cdot 10^{-11} \frac{F}{m}\) and a piezoelectric strain constant of \(d = 8 \cdot 10^{-11} \frac{m}{V}\). The dielectric material of the second device has an electric susceptibility of \(chi_e =3.2\) and a piezoelectric strain constant of \(d = 2 \cdot 10^{-10} \frac{m}{V}\).

(a) Find \(\epsilon_r\), the relative permittivity, for each device.

(b) Find \(\frac{C_1}{C_2}\), the ratio of the capacitance of the first device to the capacitance of the second device.

(c) The devices are placed in an external electric field of strength \(|\overrightarrow{E}| =32 \frac{V}{m}\). No stress is placed on the devices. Calculate the material polarization, \(\overrightarrow{P}\) for each device.

(d) The devices are placed in an external electric field of strength \(|\overrightarrow{E}| =32 \frac{V}{m}\), and a stress of \(|\overrightarrow{\varsigma}| =100 \frac{N}{m^2}\) is applied to the devices. Calculate the material polarization, \(\overrightarrow{P}\) for each device.

(e) Which device would you expect is able to store more energy? Explain your answer.

2.8. A particular piezoelectric device has a cross sectional area of \(10^{-5} m^2\). When a stress of \(800 \frac{N}{m^2}\) is applied, the device compresses by \(10 \mu m\). Under these conditions, the device can generate \(2.4 \cdot 10^{-9} J\). Calculate the efficiency of the device.

2.9. A particular piezoelectric device has a cross sectional area of \(10^{-5} m^2\) and an efficiency of 5%. When a stress of \(1640 \frac{N}{m^2}\) is applied to the device, it oscillates with an average velocity of \(0.01 \frac{m}{s}\). Calculate the power that can be generated from the device.

2.10. A piezoelectric device is placed in an electric field of strength \(|\overrightarrow{E}| =500 \frac{V}{m}\). The device is tested twice. In the first test, a stress of \(|\overrightarrow{\varsigma}| =1000 \frac{N}{m^2}\) was put on the device, and the material polarization was measured to be \(|\overrightarrow{P}| =2.75 \cdot 10^{-8} \frac{C}{m^2}\). In the second test also with \(|\overrightarrow{E}| =500 \frac{V}{m}\), a stress of \(|\overrightarrow{\varsigma}| =100 \frac{N}{m^2}\) was put on the device, and the material polarization was measured to be \(|\overrightarrow{P}| =6.50 \cdot 10^{-9} \frac{C}{m^2}\). Find the piezoelectric strain constant \(d\), and find the relative permittivity of the material \(\epsilon_r\).

2.11. According to the data sheet, a piezoelectric device is 3% efficient. A coworker says that energy is not conserved in the device because 97% of the energy is lost when it is used. Explain what is wrong with your coworker's explanation.

2.12. Match the material property with its definition. (Not all definitions will be used.)

1. A mechanical stress will cause a (material) polarization in this type of material.	A. Amorphous
2. This type of material is glassy and noncrystalline.	B. Dielectric
3. Charges do not easily flow through this type of material	C. Ferroelectric
4. In the presence of a weak external voltage, charges do not flow in this type of material. In the presence of a strong external voltage, charges flow easily.	D. Piezoelectric
5. A material polarization in one atom induces material polarization in nearby atoms in this type of material.

2.13. Consider a piezoelectric material in an external electric field \(\overrightarrow{E}\) in units V m. The figure shows the magnitude of the material polarization, \(|\overrightarrow{P}|\) in units \(\frac{C}{m^2}\), as a function of the strength of the external electric field when no mechanical stress is applied. The material has a piezoelectric strain constant of \(d = 5 \cdot 10^{-10} \frac{m}{V}\).

(a) Find the relative permittivity \(\epsilon_r\), and find the electric susceptibility \(\chi_e\).

(b) Find and plot an expression for the magnitude of the material polarization as a function of the external electric field strength when a stress of \(1000 \frac{N}{m^2}\) is applied. Label the axes of your plot well.

(c) This material is used to make a piezoelectric device with a cross sectional area of \(1 cm^2\). When this device is compressed a distance of \(1 mm\), an energy of \(2 \cdot 10^{-10} J\) is stored. Find the efficiency of the device.

2.14. Consider the 2D crystal structure, shown in the figure, composed of a lattice and a crystal basis. The crystal basis is composed of two atoms of type A and one atom of type B.

(a) Sketch the crystal basis.

(b) Sketch the 2D lattice.

(c) Draw two primitive vectors \(\overrightarrow{a}_1\) and \(\overrightarrow{a}_2\) on your sketch.

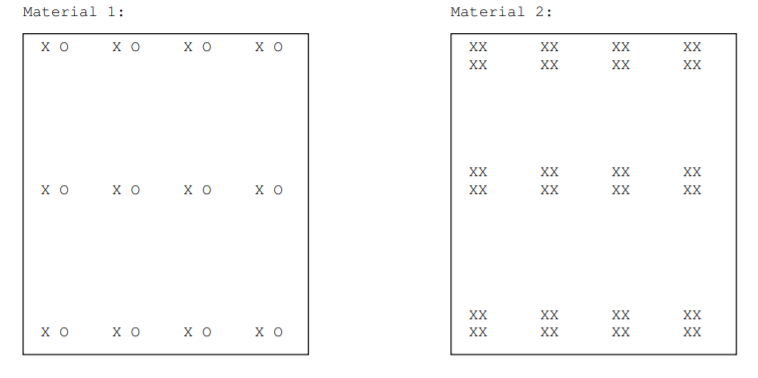
2.15. Consider the illustrations of the crystal structure of two 2D materials where X and O represent the location of different types of atoms. Do the materials have the same crystal structure? basis? lattice? crystal point group? Answer yes or no, and explain.

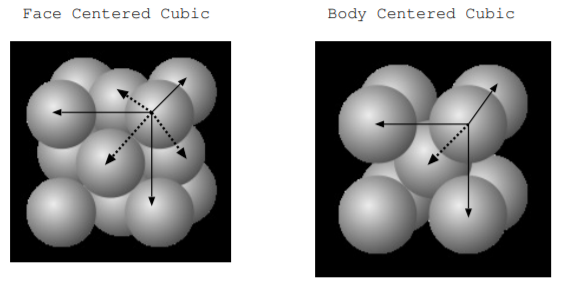
2.16. The figure below illustrates two possible crystal lattices: a face centered cubic lattice and a body centered cubic lattice. The solid arrows represent lattice vectors, but not primitive lattice vectors, and the cells shown are not primitive cells. The dotted vectors in the figure show primitive lattice vectors. In the case of the face centered cubic lattice, the primitive lattice vectors go from a corner point to a point on in the middle of one of the faces of the cube. In the body centered cubic lattice, the primitive lattice vectors go from a corner point to a point in the center of a cell bordering that corner. Suppose that the solid vectors have length 0.4 nm. Find the length of the primitive lattice vector in the face centered cubic lattice, and find the length of the primitive lattice vector in the body centered cubic lattice.