7.1: Absorption, Spontaneous Emission, Stimulated Emission
- Page ID
- 18979
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Absorption, spontaneous emission, and stimulated emission are three related energy conversion processes. Chapter 6 discussed devices based on absorption including solar cells and photodetectors. Devices which operate based on spontaneous emission include LEDs and lamps. Optical ampliers and lasers operate based on stimulated emission.
Absorption
Absorption is the process in which optical energy is converted to internal energy of electrons, atoms, or molecules. When a photon is absorbed, the energy may cause an electron in an atom to go from a lower to a higher energy level, thereby changing the internal momentum of the electron and the electron's internal quantum numbers. This process was illustrated in Chapter 6 by energy level diagrams. Energy in a solar cell or photodetector is then converted to electricity because the excited charge carriers can travel more freely through the material. The electrons absorbing the energy may be part of atoms which make up solids, liquids, gases, or plasmas. They may be around isolated neutral atoms, ionic compounds, or complicated organic molecules. Furthermore the electrons absorbing the energy may be part of conductive, insulating, or semiconducting materials. The photons absorbed may be optical photons, with individual energies in the range 1.9 to 3.1 eV that can be detected by human eyes. Alternatively, they may have energies that are multiple orders of magnitude larger or smaller than the energy of a visible photon. For example, in isolated neutral neon atoms in the ground state, electrons occupy the \(2p\) energy level but not the \(3s\) energy level. These energy levels are separated by an energy gap of \(E_g = 1.96\) eV which corresponds with energy of red photons of wavelength 632.8 nm [31]. If a photon of this energy impinges upon neon gas, the photon may be absorbed, and an electron of a neon atom would be excited to the higher energy level. Photons of smaller energy would not be absorbed. Photons of larger energy may be absorbed depending on allowed energy levels. As another example, the energy gap of the semiconductor gallium phosphide, GaP, is 2.2 eV which corresponds with the energy of a green photon of wavelength 549 nm. If a photon of this energy impinges on a piece of gallium phosphide, it may be absorbed.
Spontaneous Emission
Spontaneous emission is an energy conversion process in which an excited electron or molecule decays to an available lower energy level and in the process gives off a photon. This process occurs naturally and does not involve interaction of other photons. The average time for decay by spontaneous emission is called the spontaneous emission lifetime. For some excited energy levels this spontaneous decay occurs on average within nanoseconds while in other materials it occurs within a few seconds [10, p. 480]. As with absorption, this process can occur in isolated atoms, ionic compounds, molecules, and other types of materials, and it can occur in solids, liquids, and gases. Energy is conserved when the electron decays to the lower level, and that energy must go somewhere. The energy may be converted to heat, mechanical vibrations, or electromagnetic photons. If it is converted to photons, the process is called spontaneous emission, and the energy of the photon produced is equal to the energy dierence between the electron energy levels involved. The emitted photon may have any direction, phase, and electromagnetic polarization.
There are many ways in which an electron can be excited to a higher energy level [10, p. 455]. Spontaneous emission processes may be classified based on the source of energy which excites the electrons, and these classes are listed in Table \(\PageIndex{1}\). If the initial source of energy for spontaneous emission is supplied optically, the process is called photoluminescence. Glow in the dark materials emit light by this process. If the initial form of energy is supplied by a chemical reaction, the process is called chemiluminescence. Glow sticks produce spontaneous emission by chemiluminescence. If the initial form of energy is supplied by a voltage, the process is called electroluminescence. LEDs emit light by electroluminescence. If the initial form of energy is caused by sound waves, the process is called sonoluminescence. If the initial form of energy is due to accelerated electrons hitting a target, this process is called cathodoluminescence. If spontaneous emission occurs in a living organism, such a firefly, the process is called bioluminescence.
| Spontaneous emission energy source | |
|---|---|
| Photoluminescence | Optical electromagnetic waves |
| Chemiluminescence | Chemical reactions |
| Electroluminescence | Applied voltages |
| Sonoluminescence | Sound waves |
| Bioluminescence | Biological processes |
At temperatures above absolute zero, some electrons in atoms are thermally excited to energy levels above the ground state. These electrons decay and emit a photon by spontaneous emission. Any object at a temperature above absolute zero naturally emits photons by spontaneous emission, and this process is called blackbody radiation. In 1900, Max Planck derived a formula for the energy density per unit bandwidth of a blackbody radiator by making the assumption that only discrete energies are allowed [10, p. 453]. His work agreed with known experimental data, and it is one of the fundamental ideas of quantum mechanics. More specifically, the spectral energy density per unit bandwidth, \(u\) in units \(\frac{J \cdot s}{m^3}\), is given by
\[u= \frac{8 \pi f^2}{c^3} \cdot \frac{hf}{e^{(hf/k_BT) - 1}}. \label{7.1.1} \]
Equation \ref{7.1.1} includes a number of constants including \(c\) the speed of light in free space, \(h\) the Planck constant, and \(k_B\) the Boltzmann constant. Additionally, \(f\) is frequency in Hz, and \(T\) is temperature in kelvins. For a nice derivation, see [84, p. 186]. The first term represents the number of modes per unit frequency per unit volume while the second term represents the average energy per mode. The expression can be written as a function of wavelength instead of frequency with the substitution \(f = \frac{c}{\lambda}\).
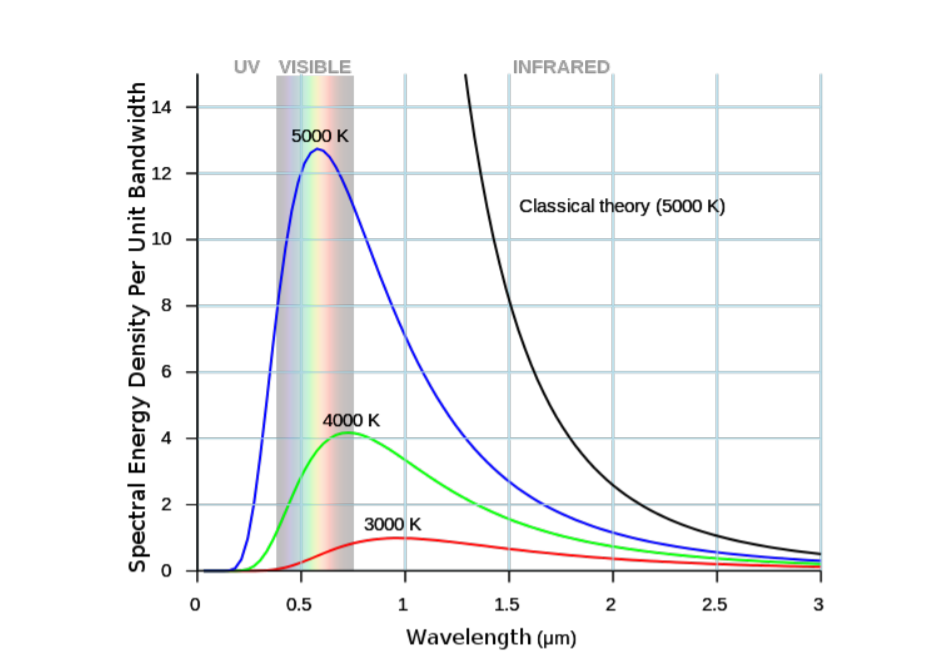
Photons emitted by a blackbody radiator have a relatively wide range of wavelengths, and this bandwidth depends on temperature. Figure \(\PageIndex{1}\) plots the energy density per unit bandwidth for blackbody radiators as a function of wavelength at temperatures 3000, 4000, and 5000 K. Room temperature corresponds to around 300 K. Visible photons have wavelengths between 400 nm \(< \lambda < \) 650 nm. From the figure, we can see that black body radiators at higher temperatures emit both more photons and have a larger fraction of photons emitted fall in the visible range.
Stimulated Emission
Stimulated emission is the process in which an excited electron or molecule interacts with a photon, decays to an available lower energy level, and in the process gives o a photon. As with the other processes, this process can occur in isolated atoms, ionic compounds, organic molecules, and other types of materials, and it can occur in solids, liquids, and gases. If an incoming photon, with energy equal to the difference between allowed energy levels, interacts with an electron in an excited state, stimulated emission can occur. The energy of the excited electron will be converted to the energy of a photon. The stimulated photon will have the same frequency, direction, phase, and electromagnetic polarization as the incoming photon which initiated the process [10, p. 436].
Rate Equations and Einstein Coefficients
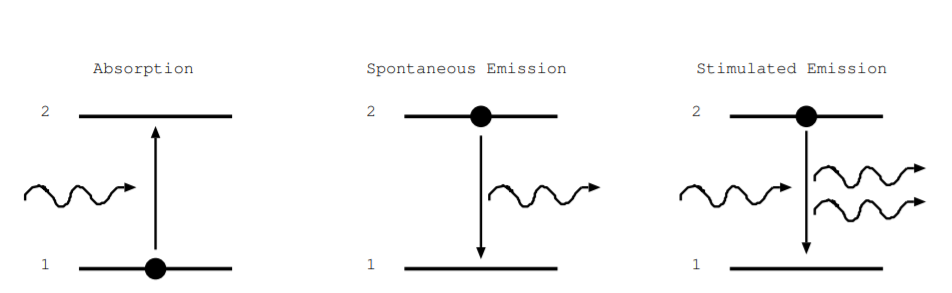
The processes of absorption, spontaneous emission, and stimulated emission are illustrated by energy level diagrams in Fig. \(\PageIndex{2}\). Energy is on the vertical axis, and nothing is plotted on the horizontal axis. Only two energy levels are shown, so this diagram illustrates only a small fraction of possible energy levels of a material. The lower energy level is labeled 1. It may represent, for example, the highest occupied energy level of an electron in an isolated atom, or it may represent the valence band of a semiconductor. The higher energy level is labeled 2, and it may represent the lowest unoccupied energy level of an electron in an isolated atom or the conduction band of a semiconductor. The dot represents an electron occupying the energy level at the start of the process. The squiggly arrows represent a photon absorbed or emitted by the process. The vertical arrow shows how the internal energy of the electron changes in the process. During absorption, an electron takes energy from an incoming photon, and the internal energy of the electron increases. During spontaneous emission, the internal energy of an electron decreases, and a photon is emitted. Stimulated emission occurs when a photon, with energy equal to the energy gap of the levels, interacts with the electron. In the process, the electron decays to the lower energy level, and a photon is produced with the same frequency, direction, phase, and electromagnetic polarization as the original photon. The figures do not illustrate a change in position of the electrons. Instead, they illustrate a change in energy and internal momentum.
The descriptions of the processes above involve changes in energy levels of an electron. However, absorption, spontaneous emission, and stimulated emission can instead involve vibrational energy states of molecules. For example, a photon may be absorbed by a molecule, and the energy may cause the molecule to go from one allowed vibrational state to another with higher internal energy. Similarly, this molecule may spontaneously decay from the higher energy state to a lower energy state emitting a photon by spontaneous emission or by stimulated emission. An example involving molecular vibration states is a carbon dioxide laser. This laser produces infrared light by stimulated emission at \(\lambda = 10.6 \mu m\), and the stimulated emission occurs between allowed vibrational energy levels of the \(\text{CO}_2\) molecule [31, p. 217]. However, to simplify the discussion in this text, we will assume that electron energy levels are involved. This assumption is true in most, but not all, energy conversion devices.
What factors determine the rate of these processes? Assume only two energy levels are involved. The number of electrons per unit volume in the lower state will be denoted \(n_1\), and the number of electrons per unit volume in the upper state will be denoted \(n_2\). The rate of absorption will be denoted \(\left.\frac{dn_2}{dt}\right|_{abs}\), the rate of spontaneous emission will be denoted \(\left.\frac{dn_2}{dt}\right|_{spont}\), and the rate of stimulated emission will be denoted \(\left.\frac{dn_2}{dt}\right|_{stim}\). Since only two energy levels are involved in this system, we can describe the rates of the processes either in terms of the upper or lower energy levels. For example, we can write the rate of absorption either as the change in population density with respect to time of the upper state or the change in population density with respect to time of the lower state.
\[\left.\frac{dn_2}{dt}\right|_{abs} = - \left.\frac{dn_1}{dt}\right|_{abs} \nonumber \]
Absorption can only occur if there is an electron present in the lower energy level. Furthermore, the rate of absorption is proportional to the number of electrons in the lower state. Additionally, the rate of absorption depends on the number of incoming photons. As in Equation \ref{7.1.1}, \(u\) represent the spectral energy density per unit bandwidth in units \(\frac{J \cdot s}{m^3}\). We can model the rate of absorption in terms of these factors [84, ch. 6] [86, ch. 7].
\[\left.\frac{dn_2}{dt}\right|_{abs} = - \left.\frac{dn_1}{dt}\right|_{abs} = B_{12}n_1u \label{7.1.3} \]
The constant of proportionality \(B_{12}\) is called an Einstein B coefficient, and it has units \(\frac{m^3}{J \cdot s^2}\).
Spontaneous emission depends on the number of electrons in the upper energy level. We can model the rate of spontaneous emission as
\[\left.\frac{dn_2}{dt}\right|_{spont} = - \left.\frac{dn_1}{dt}\right|_{spont} = -A_{21}n_2 \nonumber \]
The constant of proportionality \(A_21\) is called the Einstein A coefficient, and it has units \(\frac{1}{s}\) [84, ch. 6] [86, ch. 7]. No photons are needed to initiate spontaneous emission.
We can model the rate of stimulated emission as
\[\left.\frac{dn_2}{dt}\right|_{stim} = - \left.\frac{dn_1}{dt}\right|_{stim} = -B_{21}n_2u. \label{7.1.5} \]
The constant of proportionality \(B_21\) is known as another Einstein B coefficient, and it also has units \(\frac{m^3}{J \cdot s^2}\) [84, ch. 6] [86, ch. 7]. The rate of stimulated emission is dependent on the number of electrons in the upper energy level. Stimulated emission requires an incoming photon, so the rate also depends on the spectral energy density per unit bandwidth \(u\).
By considering the factors that affect the rate of absorption, spontaneous emission, and stimulated emission, we can see some similarities and differences in the processes. As absorption occurs, the population of electrons in the upper energy level increases, and the population of the lower energy level decreases. As both spontaneous and stimulated emission occurs, the population of the upper energy level decreases, and the population of the lower energy level increases. Both the rate of absorption and the rate of stimulated emission depend on both the population of electrons in an energy level and the energy of incoming photons while the rate of spontaneous emission does not depend on the energy of incoming photons. This similarity between absorption and stimulated emission is reflected in the rate equations, Equations \ref{7.1.3} and \ref{7.1.5}.
Einstein showed that if one of the coefficients describing the absorption, spontaneous emission, or stimulated emission is known, the other coefficients can be calculated from it. We can combine the terms above to find the overall upper state population rate.
\[\frac{dn_2}{dt} = -A_{21}n_2 + B_{12}n_1u - B_{21}n_2u \nonumber \]
At equilibrium, where photons are absorbed and emitted at the same rate, this population rate is zero.
\[\left.\frac{dn_2}{dt}\right|_{equilibrium} = 0 = -A_{21}n_2 + B_{12}n_1u - B_{21}n_2u \nonumber \]
We can solve for the energy density per unit bandwidth, \(u\).
\[B_{12}n_1u - B_{21}n_2u = A_{21}n_2 \nonumber \]
\[u = \frac{A_{21}}{\frac{n_1}{n_2}B_{12}-B_{21}} \nonumber \]
In the expression above, \(\frac{n_1}{n_2}\) represents the electron density in the lower energy state divided by the electron density in the upper state in equilibrium. This quantity is a function of temperature. Assuming many allowed energy states, the number of occupied states decreases exponentially with temperature, an idea known as Boltzmann statistics.
\[\frac{n_2}{n_1} = \frac{g_2}{g_1}e^{\frac{-hf}{k_BT}} \label{7.1.10} \]
The quantity \(\frac{g_2}{g_1}\) represents the degeneracy level which is the number of allowed electrons in the upper state over the number of allowed electrons in the lower state [84, p. 186]. In this expression, \(g_1\) and \(g_2\) are unitless measures of the number of ways electrons can occupy an energy states. Equations \ref{7.1.10} and \ref{7.1.11} can be combined.
\[u = \frac{A_{21}}{\left(\frac{g_1}{g_2}e^{\frac{-hf}{k_BT}}\right)B_{12}-B_{21}} \label{7.1.11} \]
\[u = \frac{\frac{A_{21}}{B_{21}}}{\frac{g_1B_{12}}{g_2B_{21}}e^{\frac{-hf}{k_BT}-1}} \label{7.1.12} \]
Consider a blackbody radiator, a conducting wire which is continually supplied with heat so that it remains at temperature \(T\) in equilibrium.
\[\left.\frac{dn_2}{dt}\right|_{equilibrium} = 0 \nonumber \]
One expression for the energy density per unit bandwidth of this system is given by Equation \ref{7.1.1}. Equation \ref{7.1.12} gives a second expression for the energy density per unit bandwidth, and it was found by considering the relative rates of absorption, spontaneous emission, and stimulated emission. These equations can be combined to relate the rates of the different processes.
\[\frac{8 \pi h f^{3}}{c^{3}} \cdot \frac{1}{e^{\left(h f / k_{B} T\right)}-1}=\frac{\frac{A_{21}}{B_{21}}}{\frac{g_{1} B_{12}}{g_{2} B_{21}} e^{\frac{h f}{k_{B} T}}-1} \nonumber \]
The above equation is true for the conditions
\[\frac{A_{21}}{B_{21}} = \frac{8 \pi h f^{3}}{c^{3}} \label{7.1.15} \]
and
\[\frac{g_1B_{12}}{g_2B_{21}} =1. \label{7.1.16} \]
If we know one of the Einstein coefficients, we can quickly calculate the other two Einstein coefficients from Equations \ref{7.1.15} and \ref{7.1.16}.
These equations provide further insight into the operation of lasers and other devices based on stimulated emission. The overall nonequilibrium upper state population rate is given by
\[\frac{d n_{2}}{d t}=-A_{21} n_{2}+B_{21} \frac{g_{2}}{g_{1}} n_{1} u-B_{21} n_{2} u \nonumber \]
which can be simplified with some algebra.
\[\frac{d n_{2}}{d t}=-A_{21} n_{2}-u B_{21}\left(n_{2}-\frac{g_{2}}{g_{1}} n_{1}\right) \nonumber \]
The term in parenthesis is the net upper state population. Optical amplification and lasing can only occur when the term in parenthesis is positive. The condition
\[n_2 - \frac{g_2}{g_1}n_1 >0 \nonumber \]
is called a population inversion [86, p. 189]. It only occurs when enough energy is being supplied to the system, by optical, electrical, or thermal means, so that there are more electrons in the upper energy level than the lower energy level. Population inversion has nothing to do with inversion symmetry discussed in Sec. 2.3.2. See Appendix C for a discussion of inversion and other overloaded terms.


