2.1: Electric Charge

Charging by Contact

We now know that all matter is held together by the attractive force between equal numbers of negatively charged electrons and positively charged protons. The early researchers in the 1700s discovered the existence of these two species of charges by performing experiments like those in Figures 2-1 to 2-4. When a glass rod is rubbed by a dry cloth, as in Figure 2-1, some of the electrons in the glass are rubbed off onto the cloth. The cloth then becomes negatively charged because it now has more electrons than protons. The glass rod becomes

Figure 2-1 A glass rod rubbed with a dry cloth loses some of its electrons to the cloth. The glass rod then has a net positive charge while the cloth has acquired an equal amount of negative charge. The total charge in the system remains zero.

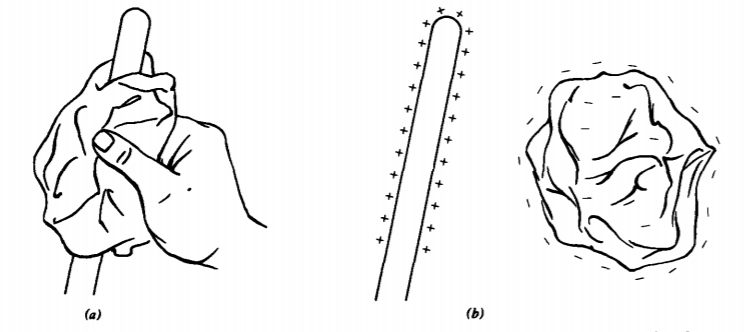
positively charged as it has lost electrons leaving behind a surplus number of protons. If the positively charged glass rod is brought near a metal ball that is free to move as in Figure 2-2a, the electrons in the ball near the rod are attracted to the surface leaving uncovered positive charge on the other side of the ball. This is called electrostatic induction. There is then an attractive force of the ball to the rod. Upon contact with the rod, the negative charges are neutralized by some of the positive charges on the rod, the whole combination still retaining a net positive charge as in Figure 2-2b. This transfer of charge is called conduction. It is then found that the now positively charged ball is repelled from the similarly charged rod. The metal ball is said to be conducting as charges are easily induced and conducted. It is important that the supporting string not be conducting, that is, insulating, otherwise charge would also distribute itself over the whole structure and not just on the ball.

If two such positively charged balls are brought near each other, they will also repel as in Figure 2-3a. Similarly, these balls could be negatively charged if brought into contact with the negatively charged cloth. Then it is also found that two negatively charged balls repel each other. On the other hand, if one ball is charged positively while the other is charged negatively, they will attract. These circumstances are summarized by the simple rules:

Opposite Charges Attract. Like Charges Repel.

Figure 2-2 (a) A charged rod near a neutral ball will induce an opposite charge on the near surface. Since the ball is initially neutral, an equal amount of positive charge remains on the far surface. Because the negative charge is closer to the rod, it feels a stronger attractive force than the repelling force due to the like charges. (b) Upon contact with the rod the negative charge is neutralized leaving the ball positively charged. (c) The like charges then repel causing the ball to deflect away.

Figure 2-3 (a) Like charged bodies repel while (b) oppositely charged bodies attract.

In Figure 2-2a, the positively charged rod attracts the negative induced charge but repels the uncovered positive charge on the far end of the ball. The net force is attractive because the positive charge on the ball is farther away from the glass rod so that the repulsive force is less than the attractive force.

We often experience nuisance frictional electrification when we walk across a carpet or pull clothes out of a dryer. When we comb our hair with a plastic comb, our hair often becomes charged. When the comb is removed our hair still stands up, as like charged hairs repel one another. Often these effects result in sparks because the presence of large amounts of charge actually pulls electrons from air molecules.

Electrostatic Induction

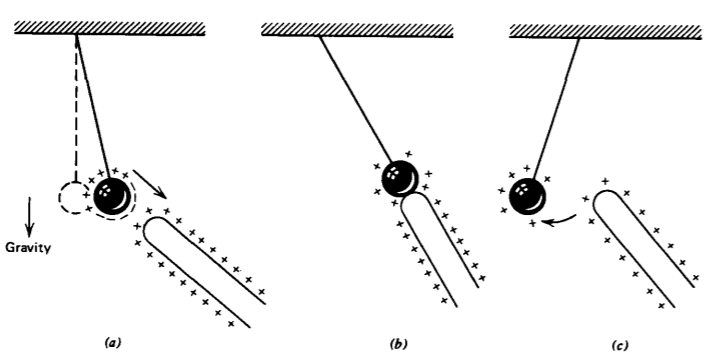
Even without direct contact net charge can also be placed on a body by electrostatic induction. In Figure 2-4a we see two initially neutral suspended balls in contact acquiring opposite charges on each end because of the presence of a charged rod. If the balls are now separated, each half retains its net charge even if the inducing rod is removed. The net charge on the two balls is zero, but we have been able to isolate net positive and negative charges on each ball.

Figure 2-4 A net charge can be placed on a body without contact by electrostatic induction. (a) When a charged body is brought near a neutral body, the near side acquires the opposite charge. Being neutral, the far side takes on an equal but opposite charge. (b) If the initially neutral body is separated, each half retains its charge.

Faraday's "Ice-Pail" Experiment

These experiments showed that when a charged conductor contacted another conductor, whether charged or not, the total charge on both bodies was shared. The presence of charge was first qualitatively measured by an electroscope that consisted of two attached metal foil leaves. When charged, the mutual repulsion caused the leaves to diverge.

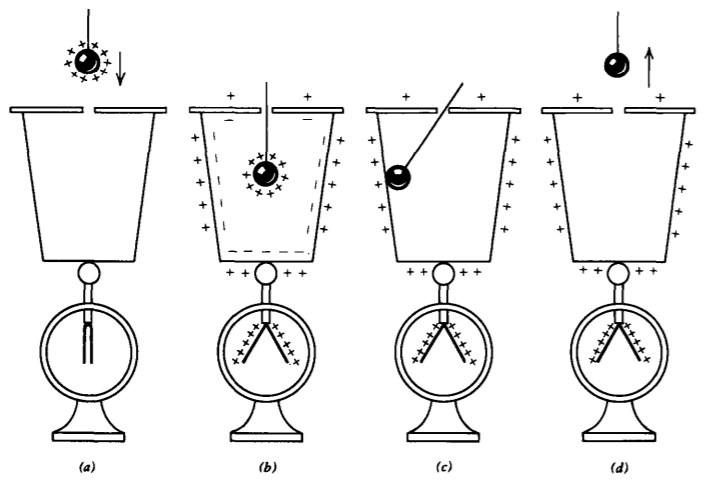
In 1843 Michael Faraday used an electroscope to perform the simple but illuminating "ice-pail" experiment illustrated in Figure 2-5. When a charged body is inside a closed isolated conductor, an equal amount of charge appears on the outside of the conductor as evidenced by the divergence of the electroscope leaves. This is true whether or not the charged body has contacted the inside walls of the surrounding conductor. If it has not, opposite charges are induced on the inside wall leaving unbalanced charge on the outside. If the charged body is removed, the charge on the inside and outside of the conductor drops to zero. However, if the charged body does contact an inside wall, as in Figure 2-5c, all the charge on the inside wall and ball is neutralized leaving the outside charged. Removing the initially charged body as in Figure 2-5d will find it uncharged, while the ice-pail now holds the original charge.

If the process shown in Figure 2-5 is repeated, the charge on the pail can be built up indefinitely. This is the principle of electrostatic generators where large amounts of charge are stored by continuous deposition of small amounts of charge.

Figure 2-5 Faraday first demonstrated the principles of charge conservation by attaching an electroscope to an initially uncharged metal ice pail. (a) When all charges are far away from the pail, there is no charge on the pail nor on the flexible gold leaves of the electroscope attached to the outside of the can, which thus hang limply. (b) As a charged ball comes within the pail, opposite charges are induced on the inner surface. Since the pail and electroscope were originally neutral, unbalanced charge appears on the outside of which some is on the electroscope leaves. The leaves being like charged repel each other and thus diverge. (c) Once the charged ball is within a closed conducting body, the charge on the outside of the pail is independent of the position of the charged ball. If the charged ball contacts the inner surface of the pail, the inner charges neutralize each other. The outside charges remain unchanged. (d) As the now uncharged ball leaves the pail, the distributed charge on the outside of the pail and electroscope remains unchanged.

This large accumulation of charge gives rise to a large force on any other nearby charge, which is why electrostatic generators have been used to accelerate charged particles to very high speeds in atomic studies.