2.8: Problems
- Page ID
- 51030
Section 2.1
Faraday's "ice-pail" experiment is repeated with the following sequence of steps:
(i) A ball with total charge \(\mathcal{Q}\) is brought inside an insulated metal ice-pail without touching.
(ii) The outside of the pail is momentarily connected to the ground and then disconnected so that once again the pail is insulated.
(iii) Without touching the pail, the charged ball is removed.
(a) Sketch the charge distribution on the inside and outside of the pail during each step.
(b) What is the net charge on the pail after the charged ball is removed
A sphere initially carrying a total charge \(\mathcal{Q}\) is brought into momentary contact with an uncharged identical sphere.
(a) How much charge is on each sphere?
(b) This process is repeated for \(N\) identical initially uncharged spheres. How much charge is on each of the spheres including the original charged sphere
(c) What is the total charge in the system after the \(N\) contacts?
Section 2.2
The charge of an electron was first measured by Robert A. Millikan in 1909 by measuring the electric field necessary to levitate a small charged oil drop against its weight. The oil droplets were sprayed and became charged by frictional electrification
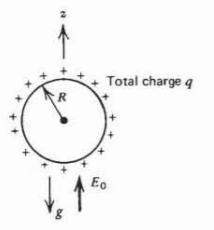
A spherical droplet of radius \(R\) and effective mass density \(\rho_{m}\) carries a total charge \(q\) in a gravity field \(g\). What electric field \(E_{0}\textrm{i}_{z}\) will suspend the charged droplet? Millikan found by this method that all droplets carried integer multiples of negative charge \(e=-1.6\times10^{19}\,\textrm{coul}\).
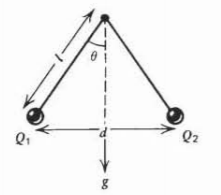
Two small conducting balls, each of mass \(m\), are at the end of insulating strings of length \(l\) joined at a point. Charges are placed on the balls so that they are a distance \(d\) apart. A charge \(\mathcal{Q}_{1}\) is placed on ball \(1\). What is the charge \(\mathcal{Q}_{2}\) on ball \(2\)?
A point charge \(-\mathcal{Q}_{1}\) of mass \(m\) travels in a circular orbit of radius \(R\) about a charge of opposite sign \(\mathcal{Q}_{2}\).
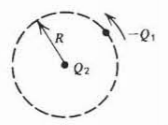
(a) What is the equilibrium angular speed of the charge \(-\mathcal{Q}_{1}\)?
(b) T his problem describes Bohr's one electron model of the atom if the charge \(-\mathcal{Q}_{1}\) is that of an electron and \(\mathcal{Q}_{2}=Ze\) is the nuclear charge, where \(Z\) is the number of protons. According to the postulates of quantum mechanics the angular momentum \(L\) of the electron must be quantized,
\(L = mvR = nh/2\pi\), \(n = 1, 2, 3, ..\)
where \(h=6.63\times 10^{-34}\,\textrm{joule-sec}\) is Planck's constant. What are the allowed values of \(R\)?
(c) For the hydrogen atom \(\left ( Z=1 \right )\) what is the radius of the smallest allowed orbit and what is the electron's orbital velocity?
An electroscope measures charge by the angular deflection of two identical conducting balls suspended by an essentially weightless insulating string of length \(l\). Each ball has mass \(M\) in the gravity field \(g\) and when charged can be considered a point charge.
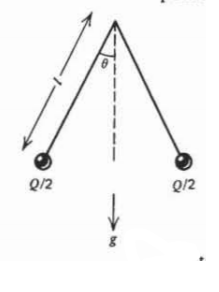
A total charge \(\mathcal{Q}\) is deposited on the two balls of the electroscope. The angle \(\theta\) from the normal obeys a relation of the for
\[\tan \theta \sin^{2} \theta = \textrm{const} \]
What is the constant?
Two point charges \(q_{1}\) and \(q_{2}\) in vacuum with respective masses \(m_{1}\) and \(m_{2}\) attract (or repel) each other via the coulomb force.

(a) Write a single differential equation for the distance between the charges \(r = r_{2} - r_{1}\). What is the effective mass of the charges? (Hint: Write Newton's law for each charge and take a mass-weighted difference.)
(b) If the two charges are released from rest at \(t=0\) when a distance \(r_{0}\) from one another, what is their relative velocity \(v = dr/dt\) as a function of \(r\)? Hint:
\[\frac{dv}{dt} = \frac{dv}{dr} \frac{dr}{dt} = v \frac{dv}{dr} = \frac{d}{dr} (\frac{1}{2} v^{2}) \]
(c) What is their position as a function of time? Separately consider the cases when the charges have the same or opposite polarity. Hint:
Let \(u = \sqrt{r}\)
\(\int \frac{u^{2}du}{\sqrt{a^{2} - u^{2}}} = -\frac{u}{2} \sqrt{a^{2} - u^{2}} + \frac{a^{2}}{2} \sin^{-1} \frac{u}{a}\)
\(\int \frac{u^{2}du}{\sqrt{u^{2}-a^{2}}} = \frac{u}{2} \sqrt{u^{2} - a^{2}} + \frac{a^{2}}{2} \ln (u + \sqrt{u^{2} - a^{2}})\)
(d) If the charges are of opposite polarity, at what time will they collide? (Hint: If you get a negative value of time, check your signs of square roots in (b).)
(e) If the charges are taken out of the vacuum and placed in a viscous medium, the velocity rather than the acceleration is proportional to the force
\(\beta_{1} \textbf{v}_{1} = \textbf{f}_{1},\) \(\beta_{2} \textbf{v}_{2} = \textbf{f}_{2}\)
where \(\beta_{1}\) and \(\beta_{2}\) are the friction coefficients for each charge. Repeat parts (a)-(d) for this viscous dominated motion
A charge \(q\) of mass \(m\) with initial velocity \(\textbf{v} = v_{0}\textbf{i}_{x}\) is injected at \(x=0\) into a region of uniform electric field \(\textbf{E} = \textbf{E}_{0}\textbf{i}_{z}\). A screen is placed at the position \(x=L\). At what height \(h\) does the charge hit the screen? Neglect gravity

A pendulum with a weightless string of length \(l\) has on its end a small sphere with charge \(q\) and mass \(m\). A distance \(D\)
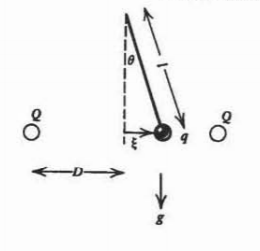
away on either side of the pendulum mass are two fixed spheres each carrying a charge \(\mathcal{Q}\). The three spheres are of sufficiently small size that they can be considered as point charges and masses.
(a) Assuming the pendulum displacement \(\xi\) to be small \(\xi <<D\)), show that Newton's law can be approximately written as
\(\frac{d^{2} \xi}{dt^{2}} + \omega_{0}^{2} \xi = 0\)
What is \(\omega^{2}_{0}\)? Hint:
\(\sin \theta \approx \frac{\xi}{l'} \: \: \frac{1}{(D \pm \xi)^{2}} \approx \frac{1}{D^{2}} \mp \frac{2 \xi}{D^{3}}\)
(b) At \(t=0\) the pendulum is released from rest with \(\xi = \xi_{0}\). What is the subsequent pendulum motion?
(c) For what values of \(q\mathcal{Q}\) is the motion unbounded with time?
Charges \(\mathcal{Q}\), \(\mathcal{Q}\), and \(q\) lie on the corners of an equilateral triangle with sides of length \(a\).
(a) What is the force on the charge \(q\)?
(b) What must \(q\) be for \(\textbf{E}\) to be zero half-way up the altitude at \(P\)?

Find the electric field along the \(z\) axis due to four equal magnitude point charges \(q\) placed on the vertices of a square with sides of length \(a\) in the \(xy\) plane centered at the origin
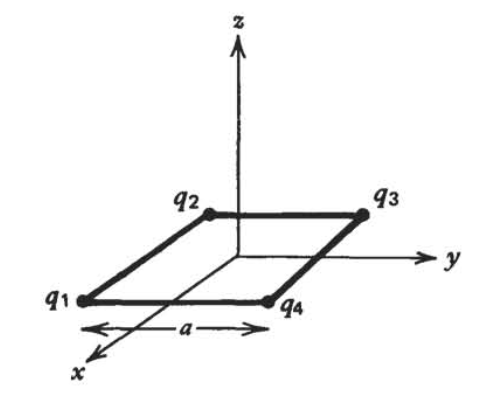
when:
(a) the charges have the same polarity, \(q_{1}=q_{2}=q_{3}=q_{4}\equiv =q\);
(b) the charges alternate in polarity, \(q_{1}=q_{3}\equiv q,\,q_{2}=q_{4}\equiv -q\);
(c) the charges are \(q_{1}=q_{2}\equiv q,\,q_{3}=q_{4}\equiv -q\).
Section 2.3
Find the total charge in each of the following distributions where \(a\) is a constant parameter:
(a) An infinitely long line charge with density
\(\lambda (z) = \lambda_{0} e^{- \vert z \vert / a}\)
(b) A spherically symmetric volume charge distributed over all space
\(\rho (r) = \frac{\rho_{0}}{[1 + r/a]^{4}}\)
(Hint: Let \(u = 1 + r/a\).)
(c) An infinite sheet of surface charge with density
\(\sigma(x, y) = \frac{\sigma_{0} e^{- \vert x \vert a}}{[1 _ (y/b)^{2}]}\)
A point charge \(q\) with mass \(M\) in a gravity field \(g\) is released from rest a distance \(x_0\) above a sheet of surface charge with uniform density \(\sigma_{0}\).
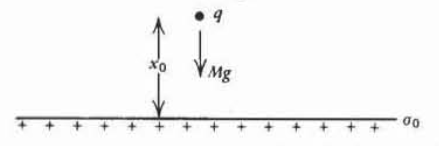
(a) What is the position of the charge as a function of time?
(b) For what value of \(\sigma_{0}\) will the charge remain stationary?
(c) If \(\sigma_{0}\) is less than the value of (b), at what time and with what velocity will the charge reach the sheet?
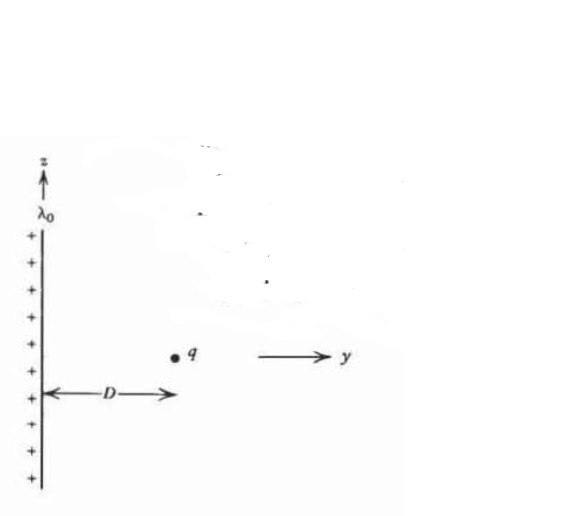
A point charge \(q\) at \(z=0\) is a distance \(D\) away from an infinitely long line charge with uniform density \(\lambda_{0}\).
(a) What is the force on the point charge \(q\)?
(b) What is the force on the line charge?
(c) Repeat (a) and (b) if the line charge has a distribution
\(\lambda (z) = \frac{\lambda_{0} \vert z \vert}{a}\)
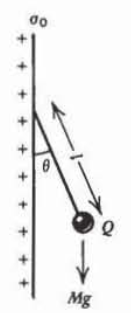
A small sphere of mass \(M\) in a gravity field \(g\) carrying a charge \(\mathcal{Q}\) is connected by a massless string to a sheet of surface charge of the same polarity with density \(\sigma_{0}\). What is the angle \(\theta\) between the sheet and charge?
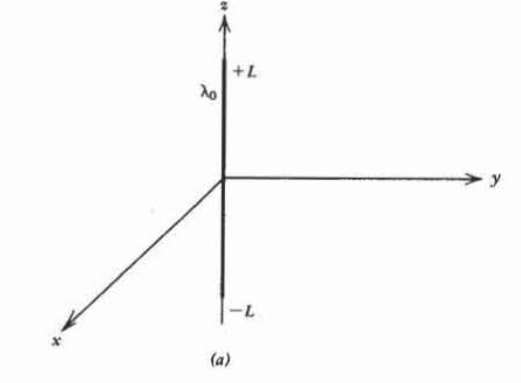
A line charge \(\lambda\) along the \(z\) axis extends over the interval \(-L \leq z \leq L\).
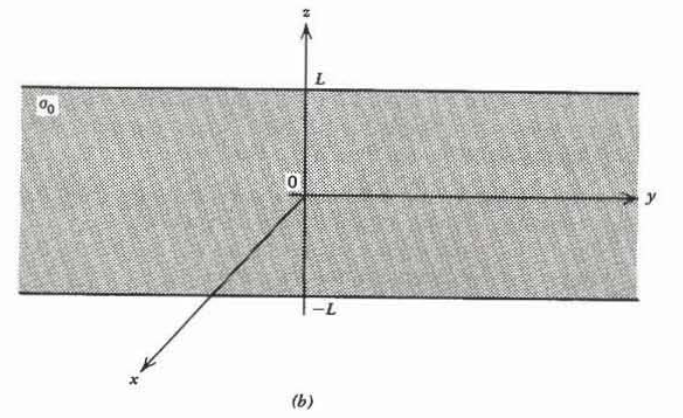
(a) Find the electric field in the \(z=0\) plane.
(b) Using the results of (a) find the electric field in the \(z=0\) plane due to an infinite strip (\(- \infty \leq y \leq \infty\)) of height \(2L\) with surgace charge density \(\sigma_{0}\). Check your results with the text for \(L \rightarrow \infty\). Hint: Let \(u = x^{2} + y^{2}\)
\(\int \frac{du}{u \sqrt{u - x^{2}} \sqrt{L^{2} + u}} = \frac{1}{Lx} \sin^{-1} (\frac{(L^{2} - x^{2}) u - 2L^{2}x^{2}}{u(L^{2} + x^{2})})\)
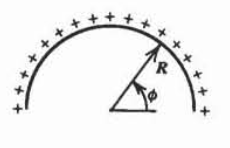
An infinitely long hollow semi-cylinder of radius \(R\) carries a uniform surface charge distribution \(\sigma_{0}\).
(a) What is the electric field along the axis of the cylinder?
(b) Use the results of (a) to find the electric field along the axis due to a semi-cylinder of volume charge \(\rho_{0}\)
(c) Repeat (a) and (b) to find the electric field at the center of a uniformly surface or volume charged hemisphere.
(a) Find the electric field along the \(z\) axis of a circular loop centered in the \(xy\) plane of radius a carrying a uniform line charge \(\lambda_{0}\) for y > 0 and \(- \lambda_{0}\) for \(y<0\).
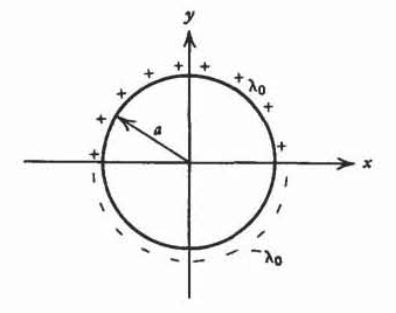
(b) Use the results of (a) to find the electric field along the z axis of a circular disk of radius a carrying a uniform surface charge \(\sigma_{0}\) for \(y>0\) and \(-\sigma_{0}\) for \(y<0\).
(a) Find the electric field along the \(z\) axis due to a square loop with sides of length \(a\) centered about the \(z\) axis in the \(xy\) plane carrying a uniform line charge \(\lambda\). What should your result approach for \(z\gg a\)?
(b) Use the results of (a) to find the electric field along the \(z\) axis due to a square of uniform surface charge \(\sigma_{0}\). What

should your result approach as \(a \rightarrow \infty\)? Hint: Let
\(u = z^{2} + \frac{x^{2}}{4}, \: \int \frac{du}{u \sqrt{2u - z^{2}}} = \frac{2}{\vert z \vert} \tan^{-1} \sqrt{\frac{2u-z^{2}}{z^{2}}}\)
A circular loop of radius \(a\) in the \(xy\) plane has a uniform line charge distribution \(\lambda_{0}\) for \(y>0\) and \(-\lambda_{0}\) for \(y<0\).
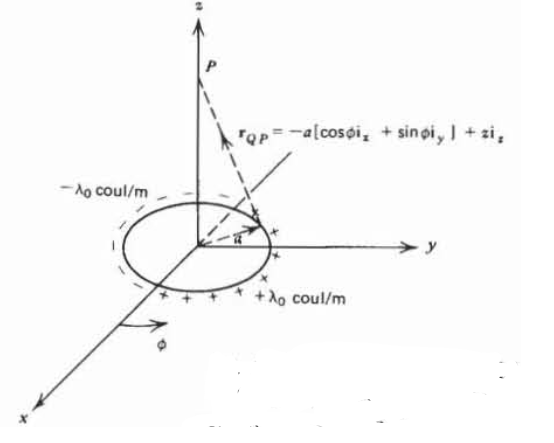
(a) What is the electric field along the \(z\) axis?
(b) Use the results of (a) to find the electric field along the \(z\) axis due to a surface charged disk, whose density is \(\sigma_{0}\) for \(y>0\) and \(-\sigma_{0}\) for \(y<0\). Hint:
\(\int \frac{\textrm{r}^{2} d \textrm{r}}{(\textrm{r}^{2} + z^{2})^{3/2}} = - \frac{\textrm{r}}{\sqrt{\textrm{r}^{2} + z^{2}}} + \ln (\textrm{r} + \sqrt{\textrm{r}^{2} + z^{2}})\)
(c) Repeat (a) if the line charge has distribution \(\lambda = \lambda_{0} \sin \phi\).
(d) Repeat (b) if the surface charge has distribution \(\sigma = \sigma_{0} \sin \phi\).
An infinitely long line charge with density \(\lambda_{0}\) is folded in half with both halves joined by a half-circle of radius \(a\). What is the electric field along the \(z\) axis passing through the center
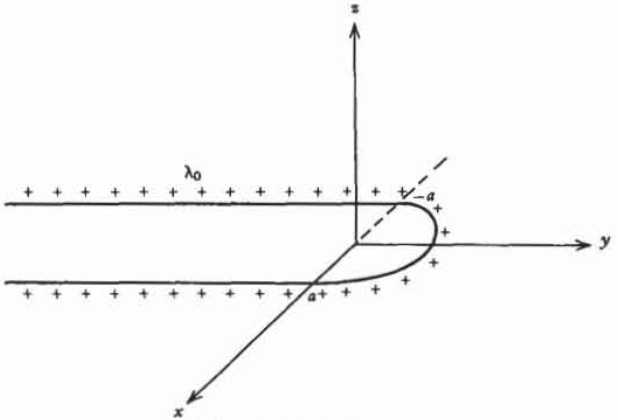
of the circle. Hint:
\(\displaystyle \int \frac{x dx}{[x^{2} + a^{2}]^{3/2}} = \frac{-1}{[x^{2} + a^{2}]^{1/2}} \\ \displaystyle \int \frac{dx}{[x^{2} + a^{2}]^{3/2}} = \frac{x}{a^{2} [x^{2} + a^{2}]^{1/2}} \\ \textbf{i}_{\textrm{r}} = \cos \phi \textbf{i}_{x} + \sin \phi \textbf{i}_{y}\)
Section 2.4
Find the total charge enclosed within each of the following volumes for the given electric fields:
(a) \(\textbf{E} = Ar^{2} \textbf{i}_{r}\) for a sphere of radius \(R\);
(b) \(\textbf{E} = A \textrm{r} \textbf{i}_{r}\) for a cylinder of radius a and length \(L\);
(c) \(\textbf{E} = A(x \textbf{i}_{x} + y \textbf{i}_{y})\) for a cube with sides of a length \(a\) having a corner at the origin.
Find the electric field everywhere for the following planar volume charge distributions:
(a) \(\rho (x) = \rho_{0} e^{- \vert x \vert /a}, \: \: \: -\infty \leq x \leq \infty\)
(b) \(\rho(x) = \left \{ \begin{matrix} - \rho_{0}, & -b \leq x \leq -a \\ \rho_{0}, & a \leq x \leq b \end{matrix} \right.\)
(c) \(\rho (x) = \frac{\rho_{0}x}{d}, \: \: \: -d \leq x \leq d \)
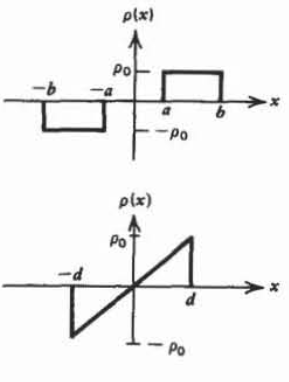
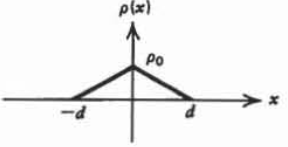
(d) \(\rho(x) = \left \{ \begin{matrix} \rho_{0}(1 + x/d), & -d \leq x \leq 0 \\ \rho_{0}(1-x/d), & 0 \leq x \leq d \end{matrix} \right.\)
Find the electric field everywhere for the following spherically symmetric volume charge distributions:
(a) \(\rho(r) = \rho_{0}e^{-r/a}, \: 0 \leq r \leq \infty\)
(Hint: \(\int r^{2} e^{-r/a} dr = -a e^{-e/a}[r^{2} + 2a^{2}(r/a + 1)].\))
(b) \(rho (r) = \left \{ \begin{matrix} \rho_{1}, & 0 \leq r < R_{1} \\ \rho_{2}, & R_{1} < r < R_{2} \end{matrix} \right. \)
(c) \(\rho(r) = \rho_{0}r/R, \quad 0 < r < R\)
Find the electric field everywhere for the following cylindrically symmetric volume charge distributions:
(a) \(\rho(\textrm{r}) = \rho_{0}e^{-\textrm{r}/a}, \: 0 < \textrm{r} < \infty\)
[Hint: \(\displaystyle \int \textrm{r} = \rho_{0} e^{-\textrm{r}/a} , \: 0 < \textrm{r} < \infty\)
(b) \(\rho(\textrm{r}) = \left \{ \begin{matrix} \rho_{1}, & 0 < \textrm{r} < a \\ \rho_{2}, & a < \textrm{r} < b \end{matrix} \right.\)
(c) \(\rho(\textrm{r}) = \rho_{0} \textrm{r}/a, \: 0 < \textrm{r} < a\)
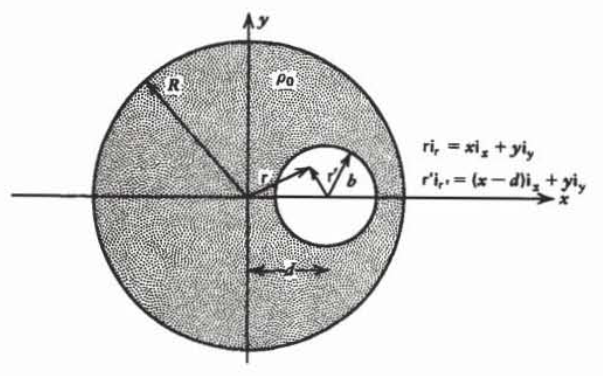
An infinitely long cylinder of radius \(R\) with uniform volume charge density \(\rho_{0}\) has an off-axis hole of radius \(b\) with center a distance \(d\) away from the center of the cylinder.
What is the electric field within the hole? (Hint: Replace the hole by the superposition of volume charge distributions of density \(\rho_{0}\) and \(-\rho_{0}\) and use the results of (27). Convert the cylindrical coordinates to Cartesian coordinates for ease of vector addition.)
Section 2.5
A line charge \(\lambda\) of length \(l\) lies parallel to an infinite sheet of surface charge \(\sigma_{0}\). How much work is required to rotate the line charge so that it is vertical?
A point charge \(q\) of mass \(m\) is injected at infinity with initial velocity \(v_{0}\textbf{i}_{x}\) towards the center of a uniformly charged sphere of radius \(R\). The total charge on the sphere \(\mathcal{Q}\) is the same sign as \(q\).
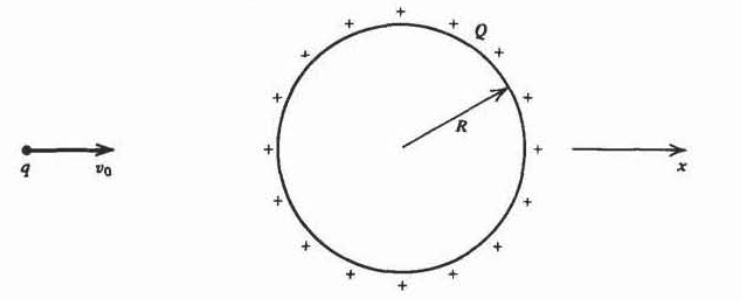
(a) What is the minimum initial velocity necessary for the point charge to collide with the sphere?
(b) If the initial velocity is half of the result in (a), how close does the charge get to the sphere?
Find the electric field and volume charge distributions for the following potential distributions:
(a) \(V = Ax^{2}\)
(b) \(V = Axyz\)
(c) \(V = A\textrm{r}^{2} \sin \phi + B \textrm{r}z\)
(d) \(V = Ar^{2} \sin \theta \cos \phi\)
Which of the following vectors can be an electric field? If so, what is the volume charge density?
(a) \(\textbf{E} = ax^{2}y^{2} \textbf{i}_{x}\)
(b) \(\textbf{E} = a(\textbf{i}_{r} \cos \theta - \textbf{i}_{\theta} \sin \theta)\)
(c) \(\textbf{E} = a(y \textbf{i}_{x} - x \textbf{i}_{y})\)
(d) \(\textbf{E} = (a/\textbf{r}^{2})[\textbf{i}_{\textrm{r}}(1 + \cos \phi) + \textbf{i}_{\phi} \sin \phi]\)
Find the potential difference \(V\) between the following surface charge distributions:
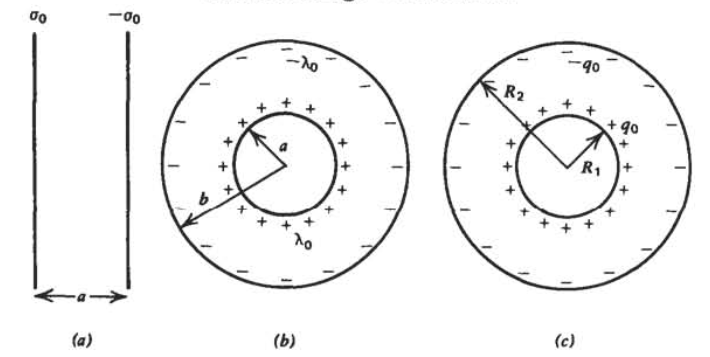
(a) Two parallel sheets of surface charge of opposite polarity \(\pm \sigma_{0}\) and spacing \(a\).
(b) Two coaxial cylinders of surface charge having infinite length and respective radii \(a\) and \(b\). The total charge per unit length on the inner cylinder is \(\lambda_{0}\) while on the outer cylinder is \(-\lambda_{0}\).
(c) Two concentric spheres of surface charge with respective radii \(R_1\) and \(R_2\). The inner sphere carries a uniformly distributed surface charge with total charge \(q_{0}\). The outer sphere has total charge \(-q_{0}\).
A hemisphere of radius \(R\) has a uniformly distributed surface charge with total charge \(\mathcal{Q}\).
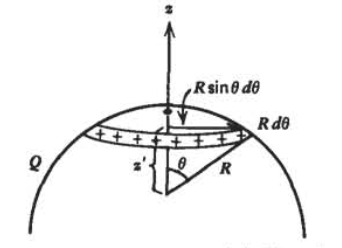
(a) Break the spherical surface into hoops of line charge of thickness \(R d \theta\). What is the radius of the hoop, its height \(z'\), and its total incremental charge \(dq\)?
(b) What is the potential along the \(z\) axis due to this incremental charged hoop? Eliminate the dependence on \(\theta\) and express all variables in terms of \(z'\), the height of the differential hoop of line charge.
(c) What is the potential at any position along the \(z\) axis due to the entire hemisphere of surface charge? Hint:
\(\int \frac{dz'}{[a + bz']^{1/2}} = \frac{2\sqrt{a + bz'}}{b}\)
(d) What is the electric field along the \(z\) axis?
(e) If the hemisphere is uniformly charged throughout its volume with total charge \(\), find the potential and electric field at all points along the \(z\) axis. (Hint: \(\int r \sqrt{z^{2} + r^{2}} dr= \frac{1}{3} (z^{2} + r^{2})^{3/2}\).)
Two point charges \(q_1\) and \(q_2\) lie along the \(z\) axis a distance \(a\) apart.
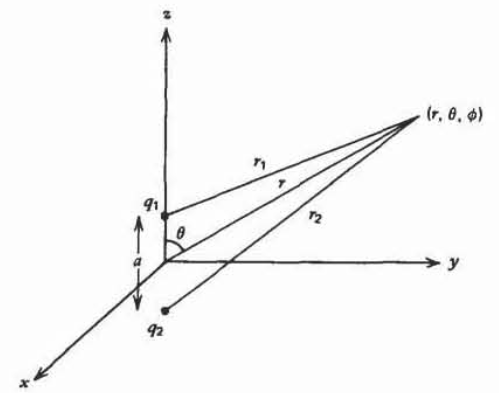
(a) Find the potential at the coordinate (\(r, \theta, \phi)\). (Hint: \(r_{1}^{2} = r^{2} + (a/2)^{2} -ar \cos \theta\).)
(b) What is the electric field?
(c) An electric dipole is formed if \(q_{2} = -q_{1}\). Find an approximate expression for the potential and electric field for points far from the dipole, \(r\gg a\).
(d) What is the equation of the field lines in this far field limit that is everywhere tangent to the electric field.
\(\frac{dr}{r d \theta} = \frac{E_{r}}{E_{\theta}}\)
Find the equation of the field line that passes through the point (\(r = r_{0}, \: \theta = \pi/2\)). (Hint: \(\int \cot \theta d \theta = \ln \sin \theta.\))
(a) Find the potentials \(V_1\), \(V_2\), and \(V_3\) at the location of each of the three-point charges shown.

(b) Now consider another set of point charges \(q'_{1}\), \(q'_{2}\), and \(q'_{3}\) at the same positions and calculate the potentials \(V'_{1}\), \(V'_{2}\), and \(V'_{3}\). Verify by direct substitution that
\(q'_{1}V_{1} + q'_{2}V_{2} + q'_{3}V_{3} = q_{1}V'_{1} + q_{2}V'_{2} + q_{3}V'_{3}\)
The generalized result for any number of charges is called Green's reciprocity theorem,
\(\sum_{i = 1}^{N} (q_{i}V'_{i}-q'_{i}V_{i}) = 0\)
(c) Show that Green's reciprocity theorem remains unchanged for perfect conductors as the potential on the conductor is constant. The \(q_{i}\) is then the charge on the conductor.
(d) A charge \(q\) at the point \(P\) is in the vicinity of a zero potential conductor. It is known that if the conductor is charged to a voltage \(V_c\), the potential at the point \(P\) in the absence of the point charge is \(V_p\). Find the total charge \(q_c\) induced on the grounded conductor. (Hint: Let \(q_{1} = q, \: q_{2} = q_{c}, \: V_{2} = 0, \: q'_{1} = 0, \: V'_{1} = V_{p}, \: V'_{2} = V_{c}.\))
(e) If the conductor is a sphere of radius \(R\) and the point \(P\) is a distance \(D\) from the center of the sphere, what is \(q_c\)? Is this result related to the method of images?
(f) A line charge \(\lambda\) is a distance \(D\) from the center of a grounded cylinder of radius \(a\). What is the total charge per unit length induced on the cylinder?
(g) A point charge \(q\) is between two zero potential perfect conductors. What is the total charge induced on each conducting surface? (Hint: Try \(q_{1} = q, \: q_{2} = q(y=0), \: q_{3} = q(y = d), \: V_{2} = 0, \: V_{3} = 0, \: q'_{1} = 0, \: V'_{2} = V_{0}, \: V'_{3} = 0.\))
(h) A point charge \(q\) travels at constant velocity \(v_{0}\) between shorted parallel plate electrodes of spacing \(d\). What is the short circuit current as a function of time?
Section 2.6
An infinitely long line charge \(\lambda\) is a distance \(D\) from the center of a conducting cylinder of radius \(R\) that carries a total charge per unit length \(\lambda_{c}\). What is the force per unit length on
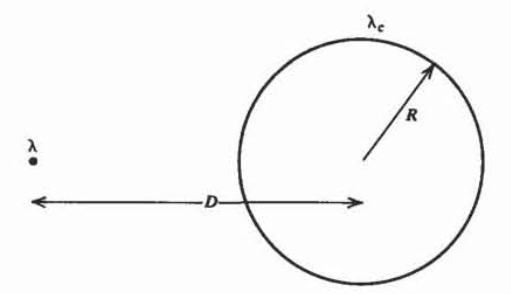
the cylinder? (Hint: Where can another image charge be place with the cylinder remaining an equipotential surface?)
An infinitely long sheet of surface charge of width \(d\) and uniform charge density \(\sigma_{0}\) is placed in the \(yz\) plane.
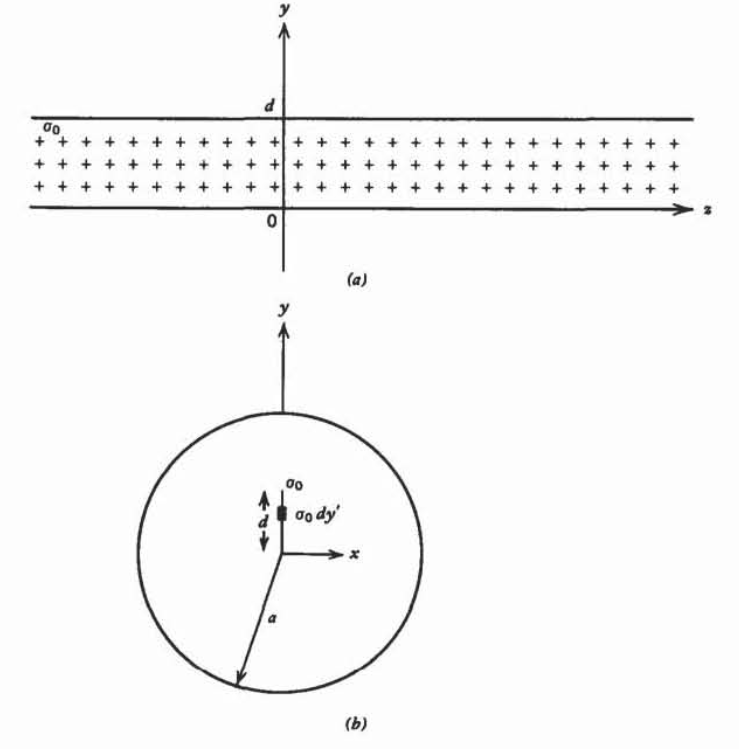
(a) Find the electric field everywhere in the \(yz\) plane. (Hint: Break the sheet into differential line charge elements \(d \lambda = \sigma_{0} d y'.\))
(b) An infinitely long conducting cylinder of radius a surrounds the charged sheet that has one side along the axis of the cylinder. Find the image charge and its location due to an incremental line charge element \(\sigma_{0} dy'\) at distance \(y'\).
(c) What is the force per unit length on the cylinder? Hint:
\(\int \ln (1-cy')dy' = -(\frac{1-cy'}{c}) [\ln (1 - cy') - 1]\)
A line charge \(\lambda\) is located at coordinate \(\left ( a,b \right )\) near a right-angled conducting corner.
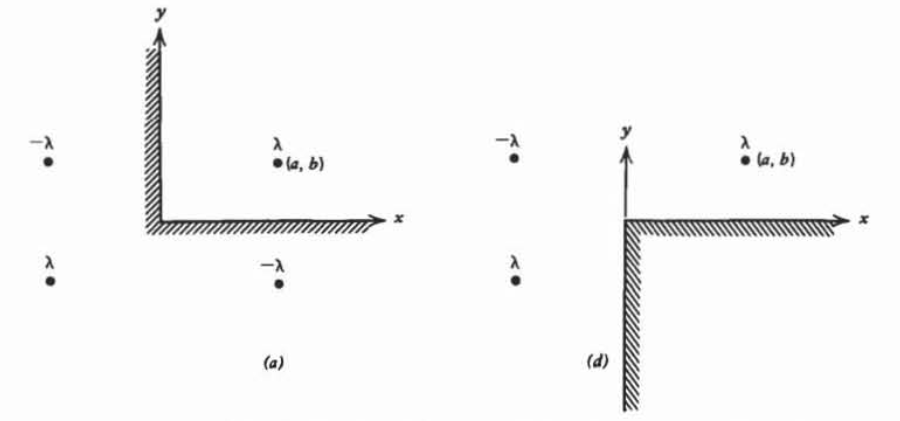
(a) Verify that the use of the three image line charges shown satisfy all boundary conditions.
(b) What is the force per unit length on \(\lambda\)?
(c) What charge per unit length is induced on the surfaces \(x=0\) and \(y=0\)?
(d) Now consider the inverse case when three line charges of alternating polarity \(\pm \lambda\) are outside a conducting corner. What is the force on the conductor?
(e) Repeat (a)-(d) with point charges.
Section 2.7
A positive point charge \(q\) within a uniform electric field \(E_{0}\textrm{i}_{x}\) from a grounded conducting plane.
(a) At what value of \(x\) is the force on the charge equal to zero?
(b) If the charge is initially at a position equal to half the value found in (a), what minimum initial velocity is necessary for the charge to continue on to \(x = = \infty\) ? (Hint: \(E_{x} = - dV/dx\).)
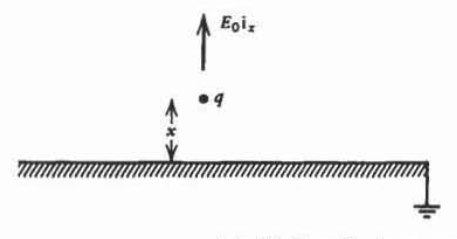
(c) If \(E_{0} = 0\), how much work is necessary to move the point charge from \(x = d\) to \(x = + \infty\)?
A sphere of radius \(R_2\) having a uniformly distributed surface charge \(\mathcal{Q}\) surrounds a grounded sphere of radius \(R_1\).
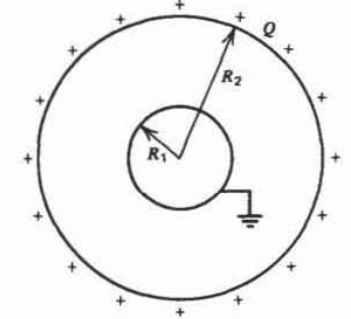
(a) What is the total charge induced on the grounded sphere? (Hint: Consider the image charge due to an incremental charge \(dq = (\mathcal{Q}/4 \pi) \sin \theta \,d \theta \,d \phi\) at \(r = R_{2}\).)
(b) What are the potential and electric field distributions everywhere?
A point charge \(q\) located a distance \(D\left ( D< R \right )\) from the center is within a conducting sphere of radius \(R\) that is at constant potential \(V_0\). What is the force on \(q\)?
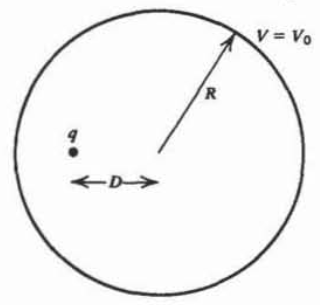
A line charge of length \(L\) with uniform density \(\lambda_{0}\) is orientated the two ways shown with respect to a grounded sphere of radius \(R\). For both cases:

(a) Consider the incremental charge element \(\lambda_{0}dz'\) a distance \(r_{QP}\) from the sphere center. What is its image charge and where is it located?
(b) What is the total charge induced on the sphere? Hint:
\(\int \frac{dz'}{\sqrt{R^{2} + z'^{2}}} = \ln (z' + \sqrt{R^{2} + z'^{2}})\)
A conducting hemispherical projection of radius \(R\) is placed upon a ground plane of infinite extent. A point charge \(d\) is placed a distance \(d\left ( d>R \right )\) above the center of the hemisphere.
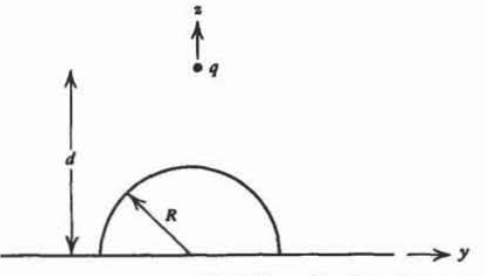
(a) What is the force on \(q\)? (Hint: Try placing three image charges along the \(z\) axis to make the plane and hemisphere have zero potential.)
(b) What is the total charge induced on the hemisphere at \(r=R\) and on the ground plane \(\vert y \vert > R\)? Hint:
\(\int \frac{\textrm{r} d \textrm{r}}{[\textrm{r}^{2} + d^{2}]^{3/2}} = \frac{-1}{\sqrt{\textrm{r}^{2} + d^{2}}}\)
A point charge \(q\) is placed between two parallel grounded conducting planes a distance \(d\) apart.
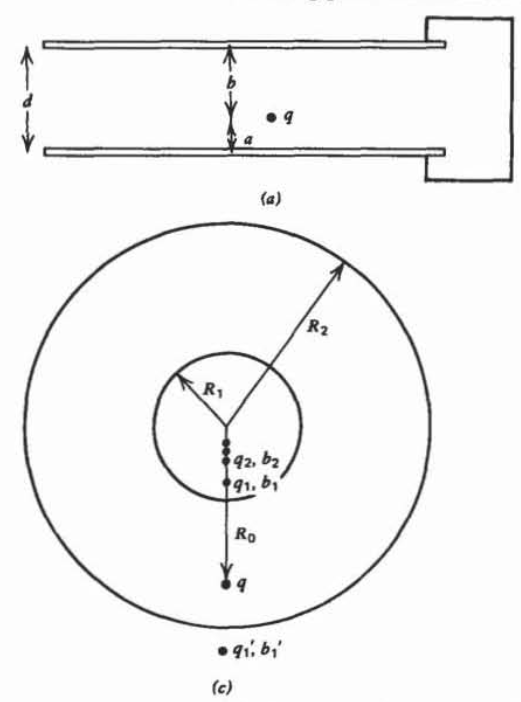
(a) The point charge \(q\) a distance \(a\) above the lower plane and a distance \(b\) below the upper conductor has summetrically located image charges. However, each image charge itself has an image in the opposite conductor. Show that an infinite number of image charges are necessary. What are the locations of these image charges?
(b) Show that the total charge on each conductor cannot be found by this method as the resulting series is divergent.
(c) Now consider a point charge \(q\), a radial distance \(R_0\) from the center of two concentric grounded conducting spheres of radii \(R_1\) and \(R_2\). Show that an infinite number of image charges in each sphere are necessary where, if we denote the \(n\)th image charge in the smaller sphere as \(q_n\) a distance \(b_n\) from the center and the nth image charge in the outer sphere as \(q'_n\) a distance \(b'_n\) from the center, then
\(q_{n+1} = -\frac{R_{1}}{b'_{n}} q'_{n}, \: \: \: q'_{n+1} = -\frac{R_{2}}{b_{n}}q_{n} \\ b_{n+1} = \frac{R^{2}_{1}}{b'_{n}}, \: \: \: b'_{n+1} = \frac{R_{2}^{2}}{b_{n}}\)
(d) Show that the equations in (c) can be simplified to
\(q_{n+1} - q_{n-1} (\frac{R_{1}}{R_{2}}) = 0 \\ b_{n+1} - b_{n-1} (\frac{R_{1}}{R_{2}})^{2} =0 \)
(e) Try power-law solutions
\(q_{n} = A \lambda^{n}, \: \: \: \: b_{n} = B \alpha^{n}\)
and find the characteristic values of \(\lambda\) and \(\alpha\) that satisfy the equations in (d).
(f) Taking a linear combinations of the solutions in (e), evaluate the unknown amplitude coefficients by substituting in values for \(n = 1\) and \(n=2\). What are all the \(q_n\) and \(b_n\)?
(g) What is the total charge induced on the inner sphere?
(Hint: \(\sum_{n=1}^{\infty} a^{n} = a/(1-a) \textrm{ for } a < 1\))
(h) Using the solutions of (\(f\)) with the difference relations of (c), find \(q'_{n}\) and \(b'_{n}\).
(i) Show that \(\sum_{n=1}^{\infty} q'_{n}\) is not a convergent series so that the total charge on the outer sphere cannot be found by this method.
(j) Why must the total induced charge on both spheres be \(-q\)? What then is the total induced charge on the outer sphere?
(k) Returning to our original problem in (a) and (b) of a point charge between parallel planes, let the radii of the spheres approach infinity such that the distances
\(d = R_{2} - R_{1}, \: \: \: \: a = R_{2} -R_{0}, \: \: \: \: b=R_{0}-R_{1}\)
remains finite. What is the total charge induced on each plane conductor?
A point charge \(\mathcal{Q}\) is a distance \(D\) above a ground plane. Directly below is the center of a small conducting sphere of radius \(R\) that rests on the plane.
(a) Find the first image charges and their positions in the sphere and in the plane.
(b) Now find the next image of each induced in the other. Show that two sets of image charges are induced on the sphere where each obey the difference equations
\(q_{n+1} = \frac{q_{n}R}{2R-b_{n}}, \: \: \: b_{n+1} = \frac{R^{2}}{2R-b_{n}}\)

(c) Eliminating the \(b_n\), show that the governing difference equation is
\(\frac{1}{q_{n+1}} - \frac{2}{q_{n}} + \frac{1}{q_{n-1}} = 0\)
Guess solutions of the form
\(P_{n} = 1/q_{n} = A \lambda^{n}\)
and find the allowed values of \(\lambda\) that satisfy the difference equation. (Hint: For double roots of \(\lambda\) the total solutions is of the form \(P_{n} = (A_{1} + A_{2}n)\lambda^{n}.\))
(d) Find all the image charges and their positions in the sphere and in the plane.
(e) Write the total charge induced n the sphere in the form
\(q_{T} = \sum_{n=1}^{\infty} \frac{A}{[1-an^{2}]}\)
What are \(A\) and \(a\)?
(f) We wish to generalize this problem to that of a sphere resting on the ground plane with an applied field \(\textbf{E}= -E_{0}\textbf{i}_{x}\) at infinity. What must the ratio \(\mathcal{Q}/D^{2}\) be, such that as \(\) and \(D\) become infinite the field far from the sphere in the \(\theta = \pi/2\) plane is \(-E_{0}\textbf{i}_{x}\)?
(g) In this limit what is the total charge induced on the sphere? (Hint: \(\sum_{n=1}^{\infty} \frac{1}{n^{2}} = \pi^{2}/6\).)
A conducting sphere of radius \(R\) at potential \(V_0\) has its center a distance \(D\) from an infinite grounded plane.
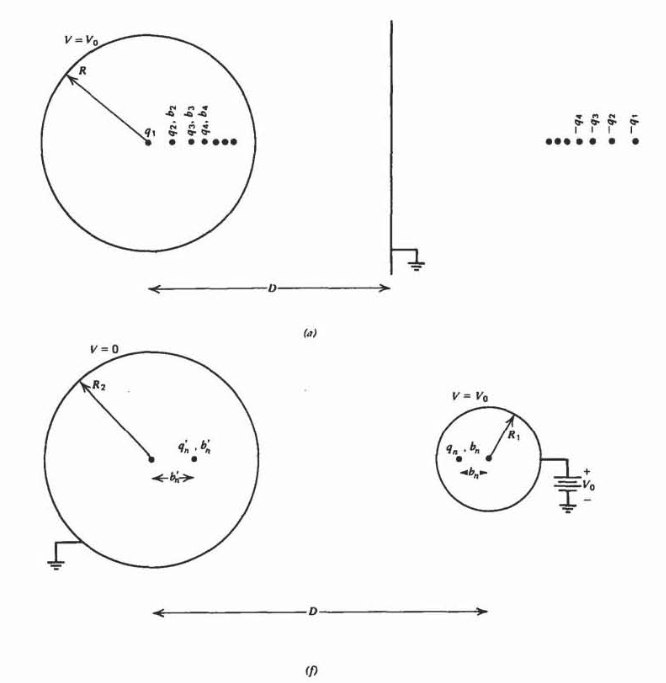
(a) Show that an infinite number of image charges in the plane and in the sphere are necessary to satisfy the boundary conditions
\(q_{n} = \frac{q_{n-1}R}{2D-b_{n-1}}, \: \: \: \: b_{n}= \frac{R^{2}}{2D-b_{n-1}}\)
What are \(q_1\) and \(q_2\)?
(b) Show that the governing difference equation is
\(\frac{1}{q_{n-1}} - \frac{c}{q_{n}} + \frac{1}{q_{n+1}} = 0\)
What is \(c\)?
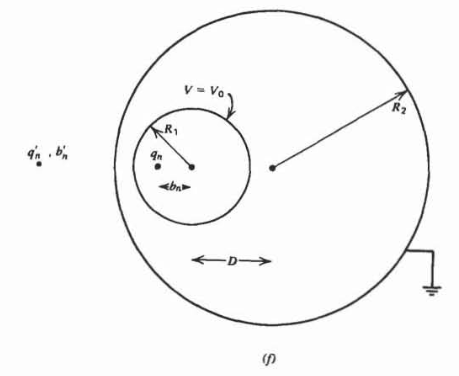
(c) Solve the difference equation in (b) assuming solutions of the form
\(P_{n} = 1/q_{n} = A \lambda^{n}\)
What values of \(\lambda\) satisfy (b)? Hint:
\(c/2 + \sqrt{(c/2)^{2}-1} = \frac{1}{c/2 - \sqrt{(c/2)^{2}-1}}\)
(d) What is the position of each image charge? What is the limiting position of the image charges as \(n \rightarrow \infty\)?
(e) Show that the capacitance (the ratio of the total charge on the sphere to the voltage \(V_0\)) can be written as an infinite series
\(C = C_{0}(\lambda^{2}-1)(\frac{1}{\lambda^{2}-1} + \frac{\lambda}{\lambda^{4}-1} + \frac{\lambda^{2}}{\lambda^{6} -1} + \frac{\lambda^{3}}{\lambda^{8}-1} + ... )\)
What are \(C_0\) and \(\lambda\)?
(f) Show that the image charges and their positions for two spheres obey the difference equations
\(q_{n+1} = \mp \frac{q'_{n}R_{1}}{D-b'_{n}}, \: \: \: \: b_{n+1} = \pm \frac{R_{1}^{2}}{D-b'_{n}} \\ q'_{n} = -\frac{R_{2}q_{n}}{D \mp b_{n}}, \: \: \: \: b'_{n} = \frac{R_{2}^{2}}{D \mp b_{n}}\)
where we use the upper signs for adjacent sphere and the lower signs when the smaller sphere of radius \(R_1\) is inside the larger one.
(g) Show that the governing difference equation is of the form
\(P_{n+1} \mp cP_{n} + P_{n-1} = 0\)
What are \(P_n\) and \(c\)?
(h) Solve (g) assuming solutions of the form
\(P_{n} = A \lambda^{n}\)
(i) Show that the capacitance is of the form
\(C = C_{0}(1 - \xi^{2}) (\frac{1}{1-\xi^{2}} + \frac{\lambda}{1 - \xi^{2}\lambda^{2}} + \frac{\lambda^{2}}{1 - \xi^{4}\lambda^{4}} + ...)\)
What are \(C_0\), \(\xi\), and \(\lambda\)?
(j) What is the capacitance when the two spheres are concentric so that \(D=0\). (Hint: \(\sum_{n=0}^{\infty} a^{n} = 1/(1-a) \textrm{ for } a<1\).)


