4.6: Problems
- Page ID
- 54811
Section 4.2
The hyperbolic electrode system of Section 4-2-2a only extends over the range \(0 \leq x \leq x_{0}, \: 0 \leq y \leq y_{0}\) and has a depth \(D\).
(a) Neglecting fringing field effects what is the approximate capacitance?
(b) A small positive test charge \(q\) (image charge effects are negligible) with mass \(m\) is released from rest from the surface of the hyperbolic electrode at \(x = x_{0}\), \(y = ab/x_{0}\). What is the velocity of the charge as a function of its position?
(c) What is the velocity of the charge when it hits the opposite electrode
A sheet of free surface charge at \(x = 0\) has charge distribution
\(\sigma_{f} = \sigma_{0} \cos a y\)
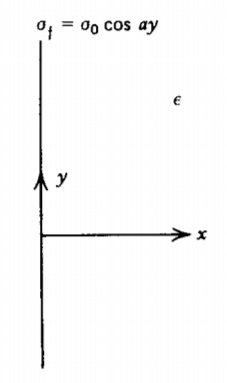
(a) What are the potential and electric field distributions?
(b) What is the equation of the field lines?
Two sheets of opposite polarity with their potential distributions constrained are a distance \(d\) apart.
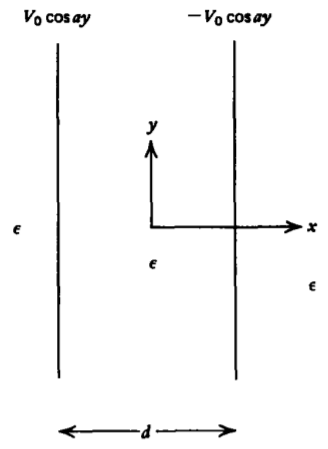
(a) What are the potential and electric field distributions everywhere?
(b) What are the surface charge distributions on each sheet?
A conducting rectangular box of width \(d\) and length \(l\) is of infinite extent in the z direction. The potential along the \(x = 0 \) edge is \(V_1\) while all other surfaces are grounded (\(V_{2} = V_{3} = V_{4} = 0\)).
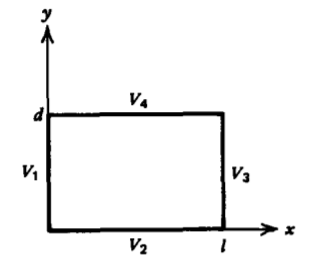
(a) What are the potential and electric field distributions?
(b) The potential at \(y = 0\) is now raised to \(V_2\) while the surface at \(x =0\) remains at potential \(V_1\). The other two surfaces remain at zero potential (\(V_{3} = V_{4} = 0\)). What are the potential and electric field distributions? (Hint: Use superposition.)
(c) What is the potential distribution if each side is respectively at nonzero potentials \(V_1\), \(V_2\), \(V_3\), and \(V_4\)?
A sheet with potential distribution
\(V = V_{0} \sin a x \cos bz\)
is placed parallel and between two parallel grounded conductors a distance \(d\) apart It is a distance \(s\) above the lower plane.
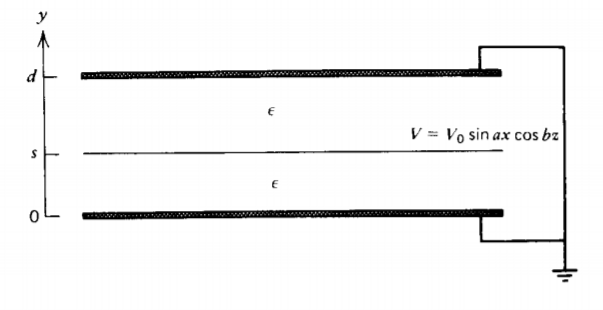
(a) What are the potential and electric field distributions? (Hint: You can write the potential distribution by inspection using a spatially shifted hyperbolic function \(\sinh c\left ( y-d \right )\).)
(b) What is the surface charge distribution on each plane at \(y=0\), \(y=s\), and \(y=d\)?
A uniformly distributed surface charge \(\sigma_{0}\) of width \(d\) and of infinite extent in the \(z\) direction is placed at \(x= 0\) perpendicular to two parallel grounded planes of spacing \(d\).
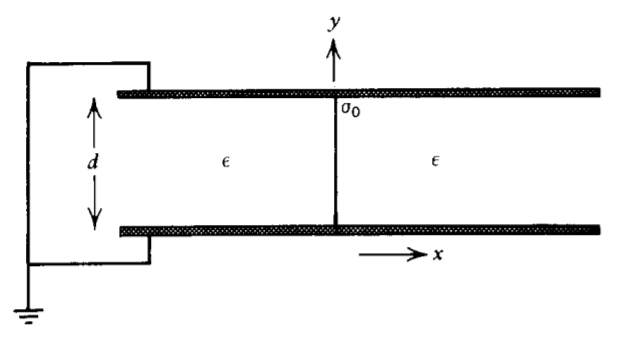
(a) What are the potential and electric field distributions? (Hint: Write \(\sigma_{0}\) as a Fourier series.)
(b) What is the induced surface charge distribution on each plane?
(c) What is the total induced charge per unit length on each plane? Hint:
\[\sum_{n=1 // n \textrm{ odd}}^{\infty} \frac{1}{n^{2}} = \frac{\pi^{2}}{8} \]
A slab of volume charge of thickness \(d\) with volume charge density \(\rho_{f} = \rho_{0} \sin ax\) is placed upon a conducting ground plane.
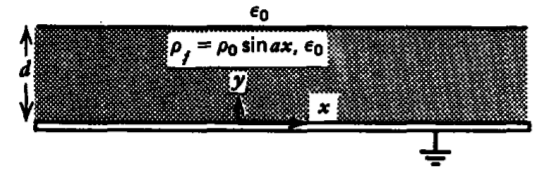
(a) Find a particular solution to Poisson's equation. Are the boundary conditions satisfied?
(b) If the solution to (a) does not satisfy all the boundary conditions, add a Laplacian solution which does.
(c) What is the electric field distribution everywhere and the surface charge distribution on the ground plane?
(d) What is the force per unit length on the volume charge and on the ground plane for a section of width \(2 \pi/a\)? Are these forces equal?
(e) Repeat (a)-(c), if rather than free charge, the slab is a permanently polarized medium with polarization
\(\textbf{P} = P_{0} \sin ax \textbf{i}_{y}\)
Consider the Cartesian coordinates \(x,y\) and define the complex quantity
\(z = x + jy, \: \: \: \: j = \sqrt{-1}\)
where z is not to be confused with the Cartesian coordinate. Any function of \(z\) also has real and imaginary parts
\(w(z) = u (x,y) + jv (x,y)\)
(a) Find \(u\) and \(v\) for the following functions:
(i) \(z^{2}\)
(ii) \(\sin z\)
(iii) \(\cos z\)
(iv) \(e^{z}\)
(v) \(\ln z \)
(b) Realizing that the partial derivatives of \(w\) are
\(\frac{\partial w}{\partial x} = \frac{dw}{d z} \frac{\partial z}{\partial x} = \frac{d w}{dz} = \frac{\partial u}{\partial x} + j \frac{\partial v}{\partial x} \\ \frac{\partial w}{\partial y} = \frac{d w}{dz} \frac{\partial z}{\partial y} = j \frac{dw}{dz} = \frac{\partial u}{\partial y} + j \frac{\partial v}{\partial y}\)
show that \(u\) and \(v\) must be related as
\(\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \: \: \: \frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x}\)
These relations are known as the Cauchy-Riemann equations and \(u\) and \(v\) are called conjugate functions.
(c) Show that both \(u\) and \(v\) obey Laplace's equation.
(d) Show that lines of constant \(u\) and \(v\) are perpendicular to each other in the \(xy\) plane. (Hint: Are \(\nabla u\) and \(\nabla v\) perpendicular vectors?)
Section 4.3
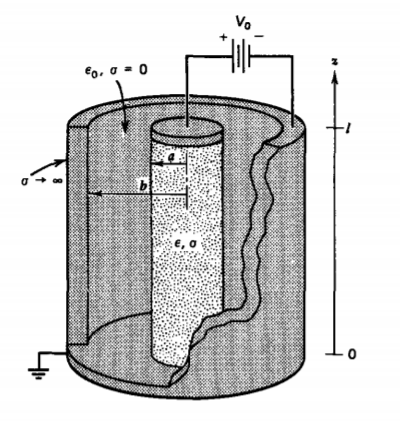
A half cylindrical shell of length \(l\) having inner radius \(a\) and outer radius \(b\) is composed of two different lossy dielectric materials (\(\varepsilon_{1}, \: \sigma_{1}\)) for \(0 < \phi < \alpha\) and (\(\varepsilon_{2}, \: \sigma_{2}\)) for \(\alpha < \phi < \pi\). A step voltage \(V_{0}\) is applied at \(t = 0\). Neglect variations with \(z\).
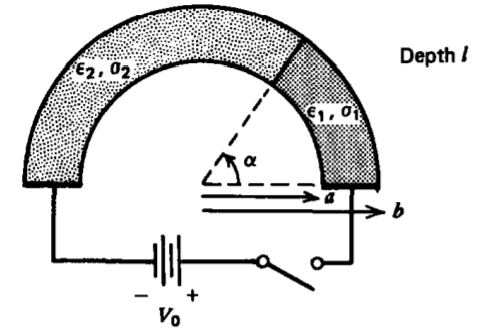
(a) What are the potential and electric field distributions within the shell at times \(t =0\), \(t = \infty\), and during the transient interval? (Hint: Assume potentials of the form \(V(\phi) = A(t) \phi + B(t)\) and neglect effects of the region outside the half cylindrical shell.)
(b) What is the time dependence of the surface charge at \(\phi = \alpha\) ?
(c) What is the resistance and capacitance?
The potential on an infinitely long cylinder is constrained to be
\(V (\textrm{r} = a) = V_{0} \sin n \phi\)
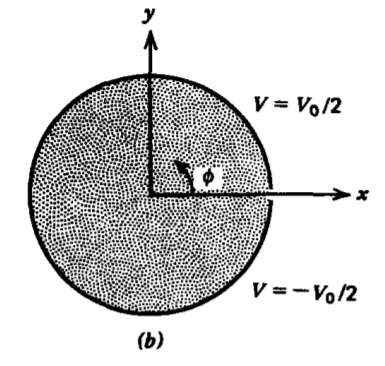
(a) Find the potential and electric field everywhere.
(b) The potential is now changed so that it is constant on each half of the cylinder:
\(V(\textrm{r} = a. \phi) = \left \{ \begin{matrix} V_{0}/2, & 0 < \phi < \pi \\ - V_{0}/2, & \pi < \phi < 2 \pi \end{matrix} \right.\)
Write this square wave of potential in a Fourier series.
(c) Use the results of (a) and (b) to find the potential and electric field due to this square wave of potential.
A cylindrical dielectric shell of inner radius a and outer radius \(b\) is placed in free space within a uniform electric field \(E_{0} \textbf{i}_{x}\). What are the potential and electric field distributions everywhere?
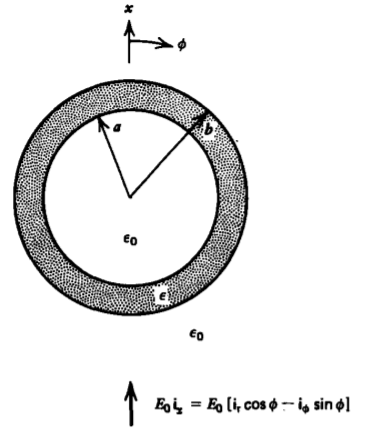
A permanently polarized cylinder \(P_{2}\textbf{i}_{x}\) of radius a is placed within a polarized medium \(P_{1}\textbf{i}_{x}\) of infinite extent. A uniform electric field \(E_{0}\textbf{i}_{x}\) is applied at infinity. There is no free charge on the cylinder. What are the potential and electric field distributions?
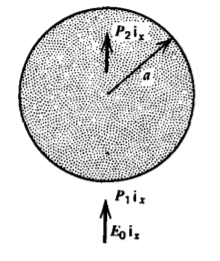
One type of electrostatic precipitator has a perfectly conducting cylinder of radius \(a\) placed within a uniform electric field \(E_{0} \textbf{i}_{x}\). A uniform flux of positive ions with charge \(q_0\) and number density \(n_0\) are injected at infinity and travel along the field lines with mobility \(\mu\). Those field lines that approach the cylinder with \(E_{\textrm{r}}< 0\) deposit ions, which redistribute themselves uniformly on the surface of the cylinder. The self-field due to the injected charge is negligible compared to \(E_0\).
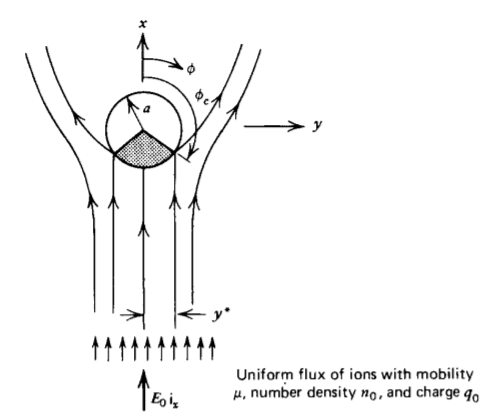
(a) If the uniformly distributed charge per unit length on the cylinder is \(\lambda(t)\), what is the field distribution? Where is the electric field zero? This point is called a critical point because ions flowing past one side of this point miss the cylinder while those on the other side are collected. What equation do the field lines obey? (Hint: To the field solution of Section 4-3-2a, add the field due to a line charge \(\lambda\).)
(b) Over what range of angle \(\phi\), \(\phi_{c} < \phi < 2 \pi - \phi_{c}\), is there a window (shaded region in figure) for charge collection as a function of \(\lambda (t)\) ? (Hint: \(E_{\textrm{r}}< 0\) for charge collection.)
(c) What is the maximum amount of charge per unit length that can be collected on the cylinder?
(d) What is the cylinder charging current per unit length? (Hint: \(dI = -q_{0} n_{0} \mu E_{r} a d \phi\))
(e) Over what range of \(y=y^{\ast }\), at \(\textrm{r}=\infty \), \(\phi = \pi\) do the injected ions impact on the cylinder as a function of \(\lambda (t)\)? What is this charging current per unit length? Compare to (d).
The cylinder of Section 4-3-2 placed within a lossy medium is allowed to reach the steady state.
(a) At \(t = 0\) the imposed electric field at infinity is suddenly set to zero. What is the time dependence of the surface charge distribution at \(\textrm{r} = a\)?
(b) Find the surface charge distribution if the field at infinity is a sinusoidal function of time \(E_{0} \cos \omega t\)
A perfectly conducting cylindrical can of radius \(c\) open at one end has its inside surface coated with a resistive layer. The bottom at \(z = 0\) and a perfectly conducting center post of radius \(a\) are at zero potential, while a constant potential \(V_0\) is imposed at the top of the can.
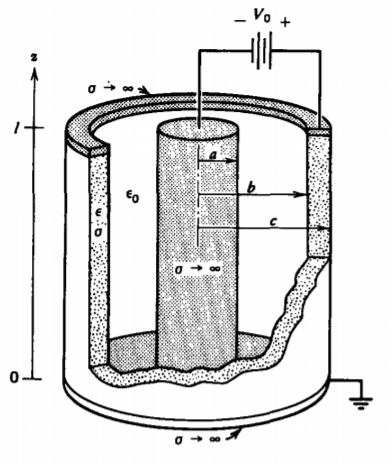
(a) What are the potential and electric field distributions within the structure \(\left ( a< \textrm{r}< c,0< z< l \right )\)? (Hint: Try the zero separation constant solutions \(n = 0\), \(k =0\).)
(b) What is the surface charge distribution and the total charge at \(\textrm{r}=a\), \(\textrm{r}=b\), and \(z =0\)?
(c) What is the equation of the field lines in the free space region?
An Ohmic conducting cylinder of radius \(a\) is surrounded by a grounded perfectly conducting cylindrical can of radius \(b\) open at one end. A voltage \(V_0\) is applied at the top of the resistive cylinder. Neglect variations with \(\phi\).
(a) What are the potential and electric field distributions within the structure, \(0< z < l\), \(0 <\textrm{r}< b\)? (Hint: Try the zero separation constant solutions \(n = 0\), \(k = 0\) in each region.)
(b) What is the surface charge distribution and total charge on the interface at \(r = a\)?
(c) What is the equation or the field lines in the free space region?
Section 4.4
A perfectly conducting hemisphere of radius \(R\) is placed upon a ground plane of infinite extent. A uniform field \(E_{0} \textbf{i}_{z}\) is applied at infinity.
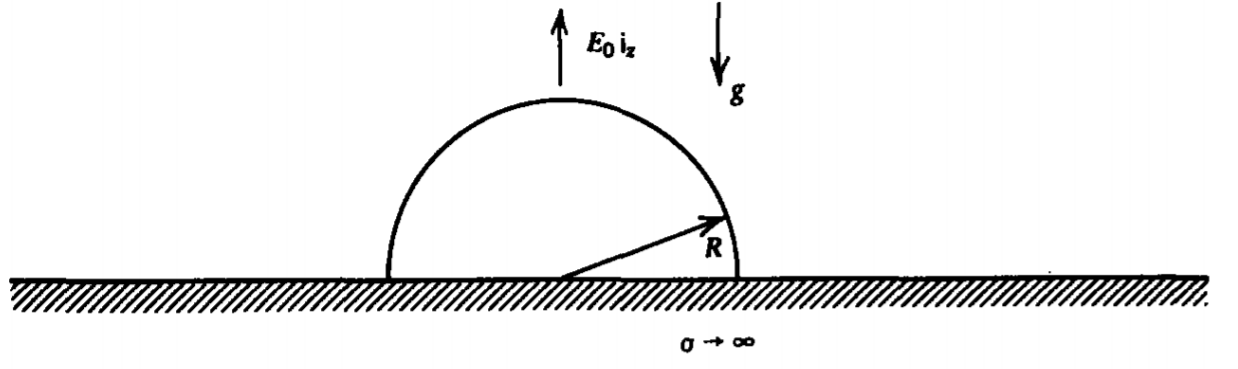
(a) How much more charge is on the hemisphere than would be on the plane over the area occupied by the hemisphere.
(b) If the hemisphere has mass density \(\rho_{m}\) and is in a gravity field \(-g \textbf{i}_{z}\), how large must \(\) be to lift the hemisphere? Hint:
\(\int \sin \theta \cos^{m} \theta d \theta = - \frac{\cos^{m+1} \theta}{m + 1}\)
A sphere of radius \(R\), permittivity \(\varepsilon_{2}\), and Ohmic conductivity \(\sigma_{2}\) is placed within a medium of permittivity \(\varepsilon_{1}\) and conductivity \(\sigma_{1}\),. A uniform electric field \(E_{0} \textbf{i}_{z}\) is suddenly turned on at \(t = 0\).
(a) What are the necessary boundary and initial conditions?
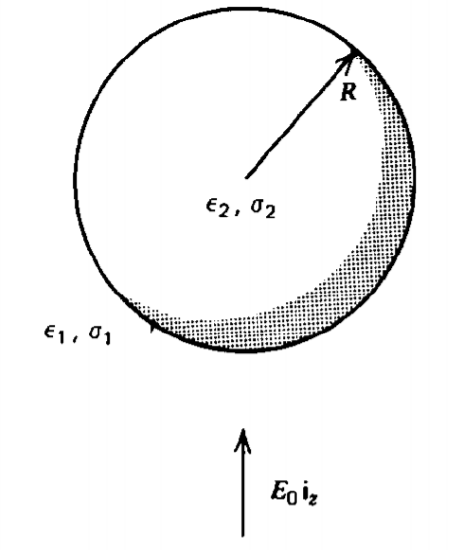
(b) What are the potential and electric field distributions as a function of time?
(c) What is the surface charge at \(r = R\)?
(d) Repeat (b) and (c) if the applied field varies sinusoidally with time as \(E_{0} \cos \omega t\) and has been on a long time.
The surface charge distribution on a dielectric sphere with permittivity \(\varepsilon_{2}\) and radius R is
\(\sigma_{f} = \sigma_{0} (3 \cos^{2} \theta -1)\)
The surrounding medium has permittivity \(\varepsilon_{1}\). What are the potential and electric field distributions? (Hint: Try the \(n = 2\) solutions.
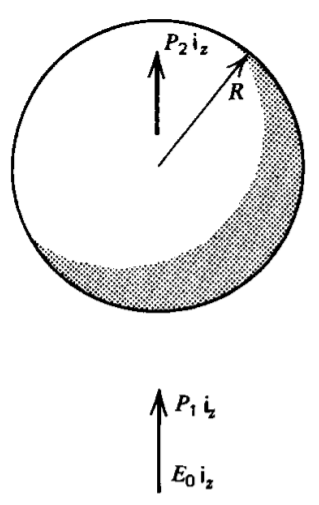
A permanently polarized sphere \(P_{2} \textbf{i}_{z}\) of radius \(R\) is placed within a polarized medium \(P_{1} \textbf{i}_{z}\). A uniform electric field \(E_{0} \textbf{i}_{z}\) is applied at infinity. There is no free charge at \(r = R\). What are the potential and electric field distributions?
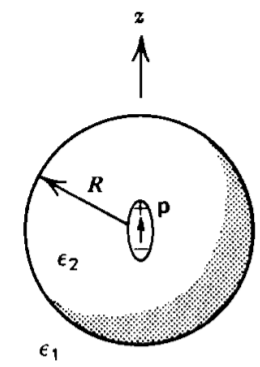
A point dipole \(\textbf{p} = p \textbf{i}_{z}\), is placed at the center of a dielectric sphere that is surrounded by a different dielectric medium. There is no free surface charge on the interface. What are the potential and electric field distributions? Hint:
\(\lim_{r \rightarrow 0} V (r, \theta) = \frac{p \cos \theta}{4 \pi \varepsilon_{2} r^{2}}\)
Section 4.5
The conducting box with sides of length \(d\) in Section 4-5-2 is filled with a uniform distribution of volume charge with density
\(\rho_{0} = - \frac{72 \varepsilon_{0}}{d^{2}} [ \textrm{coul m}^{-3}]\)
What are the potentials at the four interior points when the outside of the box is grounded?
Repeat the relaxation procedure of Section 4-5-2 if the boundary potentials are:
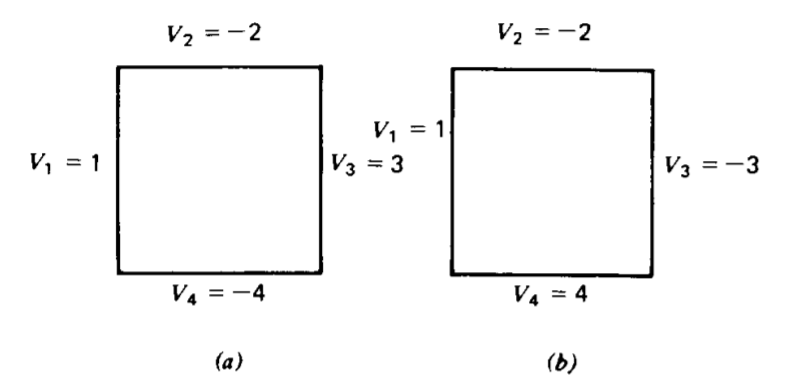
(a) \(V_1\) = 1, \(V_2\) = -2, \(V_3\) = 3, \(V_4\) = -4
(b) \(V_1\)= 1, \(V_2\) = -2, \(V_3\) = -3, \(V_4\) = 4
(c) Compare to four decimal places with the exact solution.


