6.7: Problems
- Page ID
- 83698
Section 6-1
A circular loop of radius \(a\) with Ohmic conductivity \(\sigma \) and cross-sectional area \(A\) has its center a small distance \(D\) away from an infinitely long time varying current.

(a) Find the mutual inductance \(M\) and resistance \(R\) of the loop. Hint:
\(\begin{align}&\int \frac{dx}{a+b\cos x}=\frac{2}{\sqrt{a^{2}-b^{2}}}\tan ^{-1}\left [ \frac{\sqrt{a^{2}-b^{2}}\tan \left ( x/2 \right )}{a+b} \right ], \\ & \int \frac{rdr}{\sqrt{D^{2}-r^{2}}}=-\sqrt{D^{2}-r^{2}}\end{align}\)
(b) This loop is stationary and has a self-inductance \(L\). What is the time dependence of the induced short circuit current when the line current is instantaneously stepped on to a dc level \(I\) at \(t = 0\)?
(c) Repeat (b) when the line current has been on a long time and is suddenly turned off at \(t = T\).
(d) If the loop has no resistance and is moving with radial velocity \(v_{r}=dr/dt\), what is the short circuit current and open circuit voltage for a dc line current?
(e) What is the force on the loop when it carries a current \(i\)? Hint:
\(\int \frac{\cos \phi d\phi }{D+a\cos \phi }=-\frac{1}{a}\sin ^{-1}\left [ \cos \phi \right ]+\frac{D}{a\sqrt{D^{2}-a^{2}}}\sin ^{-1}\left ( \frac{a+D\cos \phi }{D+a\cos \phi } \right )\)
A rectangular loop at the far left travels with constant velocity \(U\textbf{i}_{x}\) towards and through a dc surface current sheet \(K_{0}\textbf{i}_{y}\) at \(x =0\). The right-hand edge of the loop first reaches the current sheet at \(t =0\).
(a) What is the loop's open circuit voltage as a function of time?
(b) What is the short circuit current if the loop has self-inductance \(L\) and resistance \(R\)?
(c) Find the open circuit voltage if the surface current is replaced by a fluid with uniformly distributed volume cur rent. The current is undisturbed as the loop passes through.
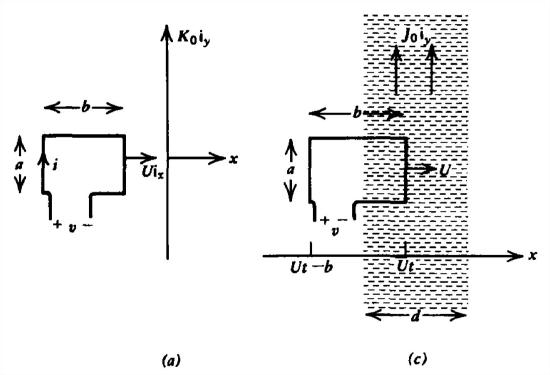
Specifically consider the case when \(d>b\) and then sketch the results when \(d= b\) and \(d<b\). The right edge of the current loop reaches the volume current at \(t =0\).
A short circuited rectangular loop of mass \(m\) and self-inductance \(L\) is dropped with initial velocity \(v_{0}\textbf{i}_{x}\) between the pole faces of a magnet that has a concentrated uniform magnetic field \(B_{0}\textbf{i}_{z}\). Neglect gravity.
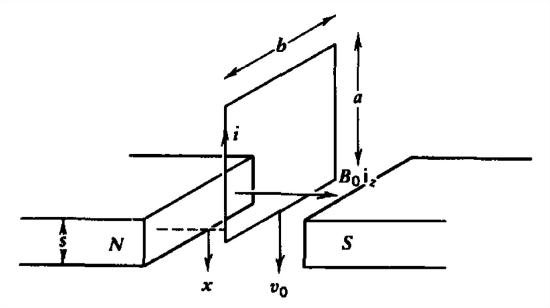
(a) What is the imposed flux through the loop as a function of the loop's position \(x\left ( 0< x< s \right )\) within the magnet?
(b) If the wire has conductivity \(\sigma \) and cross-sectional area \(A\), what equation relates the induced current \(i\) in the loop and the loop's velocity?
(c) What is the force on the loop in terms of \(i\)? Obtain a single equation for the loop's velocity. (Hint: Let \(\omega_{0}^{2}=B_{0}^{2}b^{2}/mL,\quad \alpha =R/L\).)
(d) How does the loop's velocity and induced current vary with time?
(e) If \(\sigma \rightarrow \infty \), what minimum initial velocity is necessary for the loop to pass through the magnetic field?
Find the mutual inductance between the following cur rents:
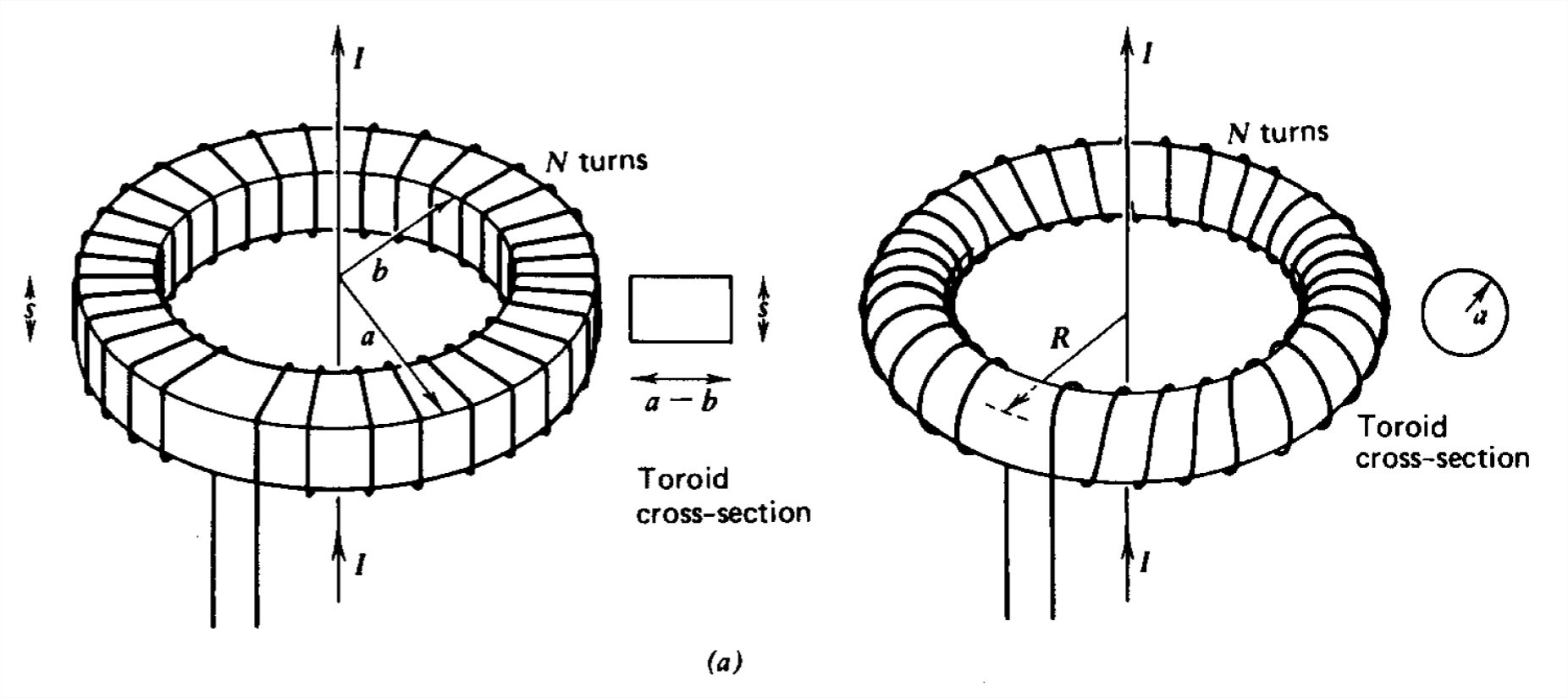
(a) Toroidal coil of rectangular or circular cross section coaxially centered about an infinitely long line current. Hint:
\(\begin{align}&\int \frac{dx}{a+b\cos x}=\frac{2}{\sqrt{a^{2}-b^{2}}}\tan ^{-1}\left [ \frac{\sqrt{a^{2}-b^{2}}\tan \left ( x/2 \right )}{a+b} \right ], \\ & \int \frac{rdr}{\sqrt{R^{2}-r^{2}}}=-\sqrt{R^{2}-r^{2}}\end{align}\)
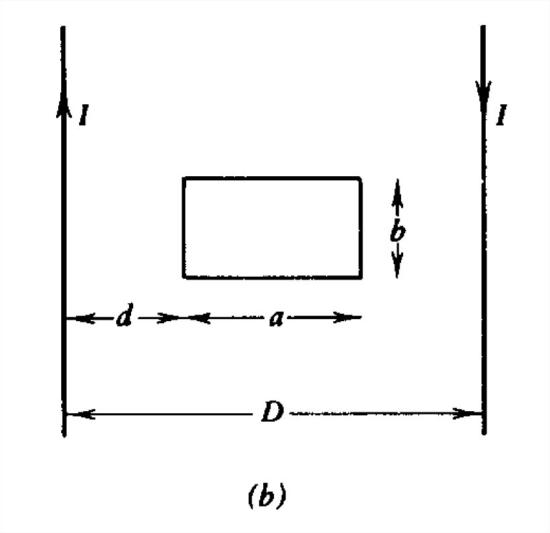
(b) A very long rectangular current loop, considered as two infinitely long parallel line currents, a distance \(D\) apart, carrying the same current \(I\) in opposite directions near a small rectangular loop of width \(a\), which is a distance \(d\) away from the left line current. Consider the cases \(d+a<D\), \(d< D< d+a\), and \(d>D\).
A circular loop of radius a is \(a\) distance \(D\) above a point magnetic dipole of area \(dS\) carrying a current \(I_{1}\).
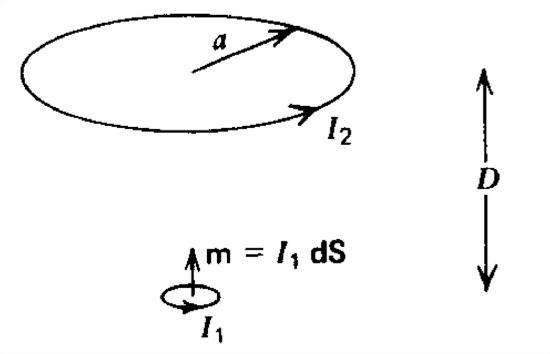
(a) What is the vector potential due to the dipole at all points on the circular loop? (Hint: See Section 5-5-1.)
(b) How much flux of the dipole passes through the circular loop?
(c) What is the mutual inductance between the dipole and the loop?
(d) If the loop carries a current \(I_{2}\), what is the magnetic field due to \(I_{2}\) at the position of the point dipole? (Hint: See Section 5-2-4a.)
(e) How much flux due to \(I_{2}\) passes through the magnetic dipole?
(f) What is the mutual inductance? Does your result agree with (c)?
A small rectangular loop with self-inductance \(L\), Ohmic conductivity \(\sigma \), and cross-sectional area \(A\) straddles a current sheet.
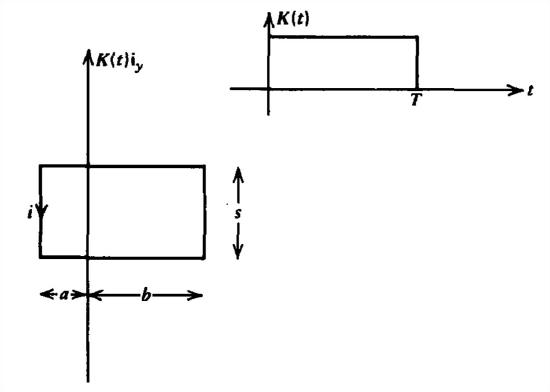
(a) The current sheet is instantaneously turned on to a dc level \(K_{0}\textbf{i}_{y}\) at \(t =0\). What is the induced loop current?
(b) After a long time \(T\) the sheet current is instantaneously set to zero. What is the induced loop current?
(c) What is the induced loop current if the current sheet varies sinusoidally with time as \(K_{0}\cos \omega t\textbf{i}_{y}\).
A point magnetic dipole with area \(d\textrm{S}\) lies a distance \(d\) below a perfectly conducting plane of infinite extent. The dipole current \(I\) is instantaneously turned on at \(t =0\).
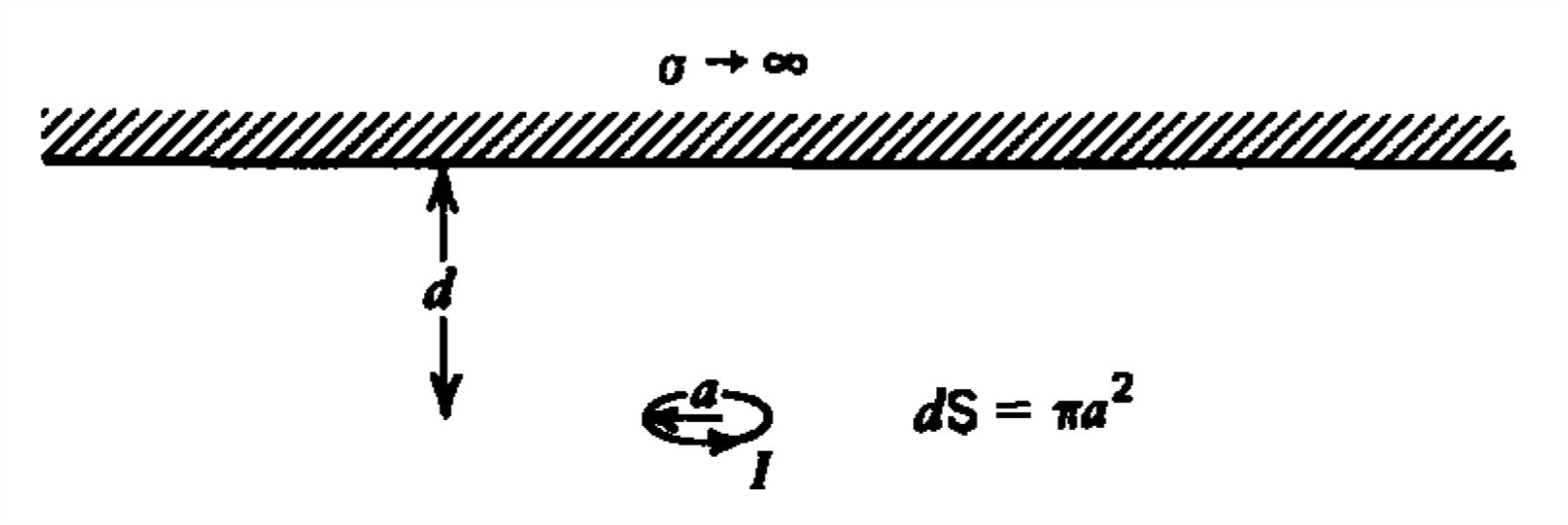
(a) Using the method of images, find the magnetic field everywhere along the conducting plane. (Hint: \(\textbf{i}_{r}\cdot \textbf{i}_{r}=\sin \theta, \quad \textbf{i}_{\theta }\cdot \textbf{i}_{r}=\cos \theta\))
(b) What is the surface current distribution?
(c) What is the force on the plane? Hint:
\(\int \frac{\textrm{r}^{3}d\textrm{r}}{\left ( \textrm{r}^{2}+d^{2} \right )^{5}}=-\frac{\left ( \textrm{r}^{2}+d^{2}/4 \right )}{6\left ( \textrm{r}^{2}+d^{2} \right )^{4}}\)
(d) If the plane has a mass \(M\) in the gravity field \(g\), what current \(I\) is necessary to just lift the conductor? Evaluate for \(M=10^{-3}\,\textrm{kg}\), \(d=10^{-2}\,\textrm{m}\), and \(a=10^{-3}\,\textrm{m}\).
A thin block with Ohmic conductivity \(\sigma \) and thickness \(\delta \) moves with constant velocity \(V\textbf{i}_{x}\) between short circuited perfectly conducting parallel plates. An initial surface current \(K_{0}\) is imposed at \(t =0\) when \(x=x_{0}\), but the source is then removed.
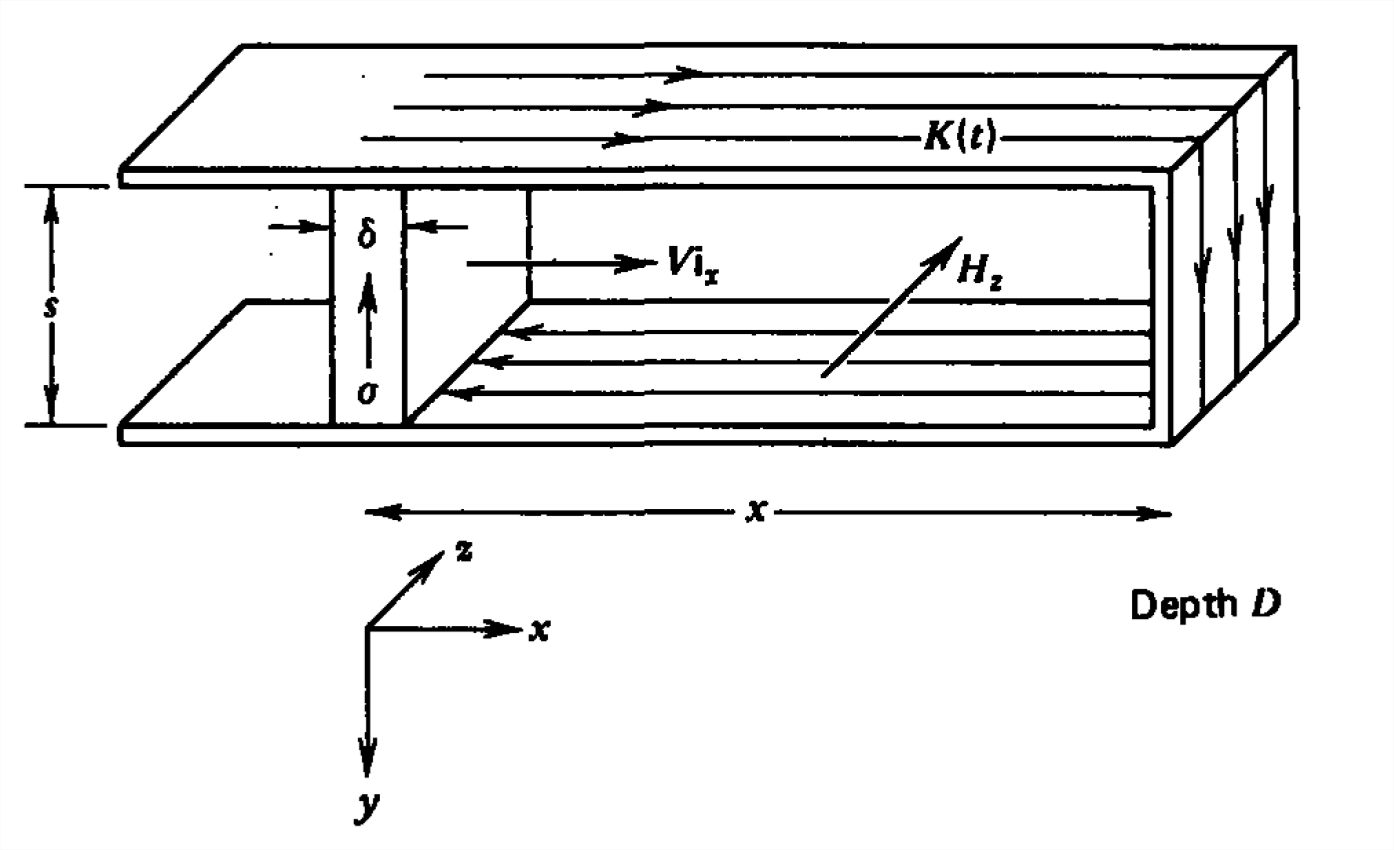
(a) The surface current on the plates \(K(t\)) will vary with time. What is the magnetic field in terms of \(K(t)\)? Neglect fringing effects.
(b) Because the moving block is so thin, the current is uniformly distributed over the thickness \(\delta \). Using Faraday's law, find \(K(t)\) as a function of time.
(c) What value of velocity will just keep the magnetic field constant with time until the moving block reaches the end?
(d) What happens to the magnetic field for larger and smaller velocities?
A thin circular disk of radius \(a\), thickness \(d\), and conductivity \(\sigma \) is placed in a uniform time varying magnetic field \(B(t)\).
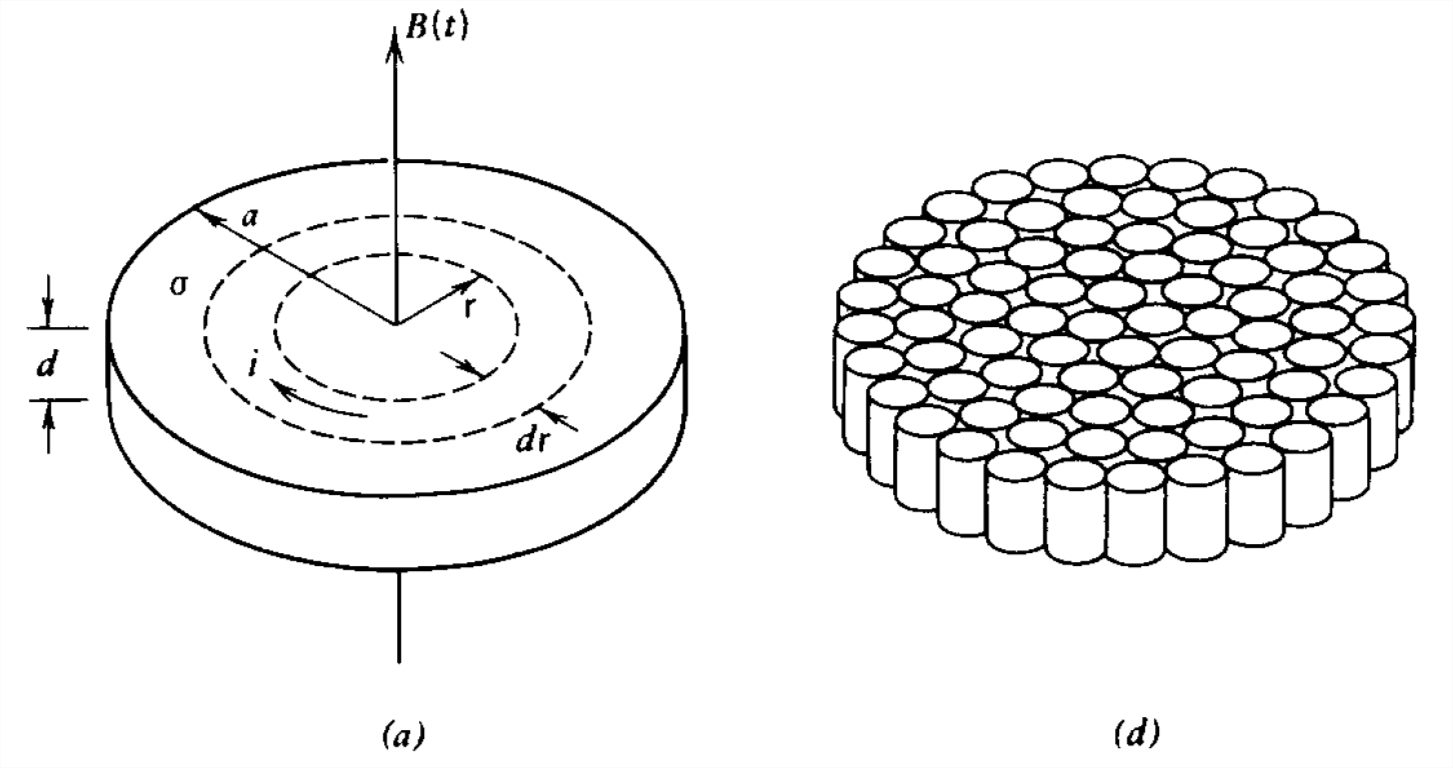
(a) Neglecting the magnetic field of the eddy currents, what is the current induced in a thin circular filament at radius \(\textrm{r}\) of thickness \(d\textrm{r}\).
(b) What power is dissipated in this incremental current loop?
(c) How much power is dissipated in the whole disk?
(d) If the disk is instead cut up into \(N\) smaller circular disks with negligible wastage, what is the approximate radius of each smaller disk?
(e) If these \(N\) smaller disks are laminated together to form a thin disk of closely packed cylindrical wires, what is the power dissipated?
Section 6-2
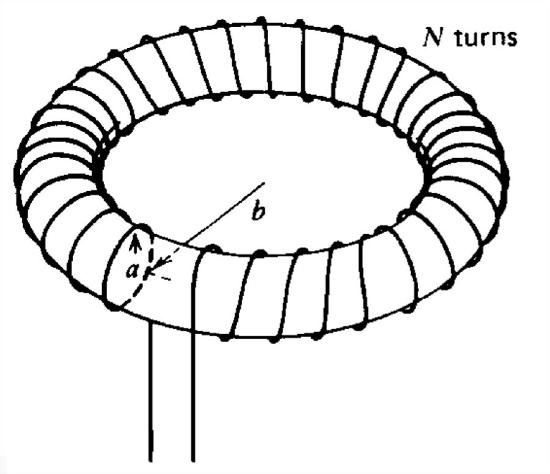
Find the self-inductance of an \(N\) turn toroidal coil of circular cross-sectional radius \(a\) and mean radius \(b\). Hint:
\(\begin{align} &\int \frac{d\theta }{b+\textrm{r}\cos \theta }=\frac{2}{\sqrt{b^{2}-\textrm{r}^{2}}}\tan ^{-1}\frac{\sqrt{b^{2}-\textrm{r}^{2}}\tan \left ( \theta /2 \right )}{b+\textrm{r}} \\
&\int \frac{\textrm{r}d\textrm{r}}{\sqrt{b^{2}-\textrm{r}^{2}}}=-\sqrt{b^{2}-\textrm{r}^{2}}\end{align} \)
A large solenoidal coil of long length \(l_{1}\), radius \(a_{1}\), and number of turns \(N_{1}\) coaxially surrounds a smaller coil of long length \(l_{2}\), radius \(a_{1}\), and turns \(N_{1}\).
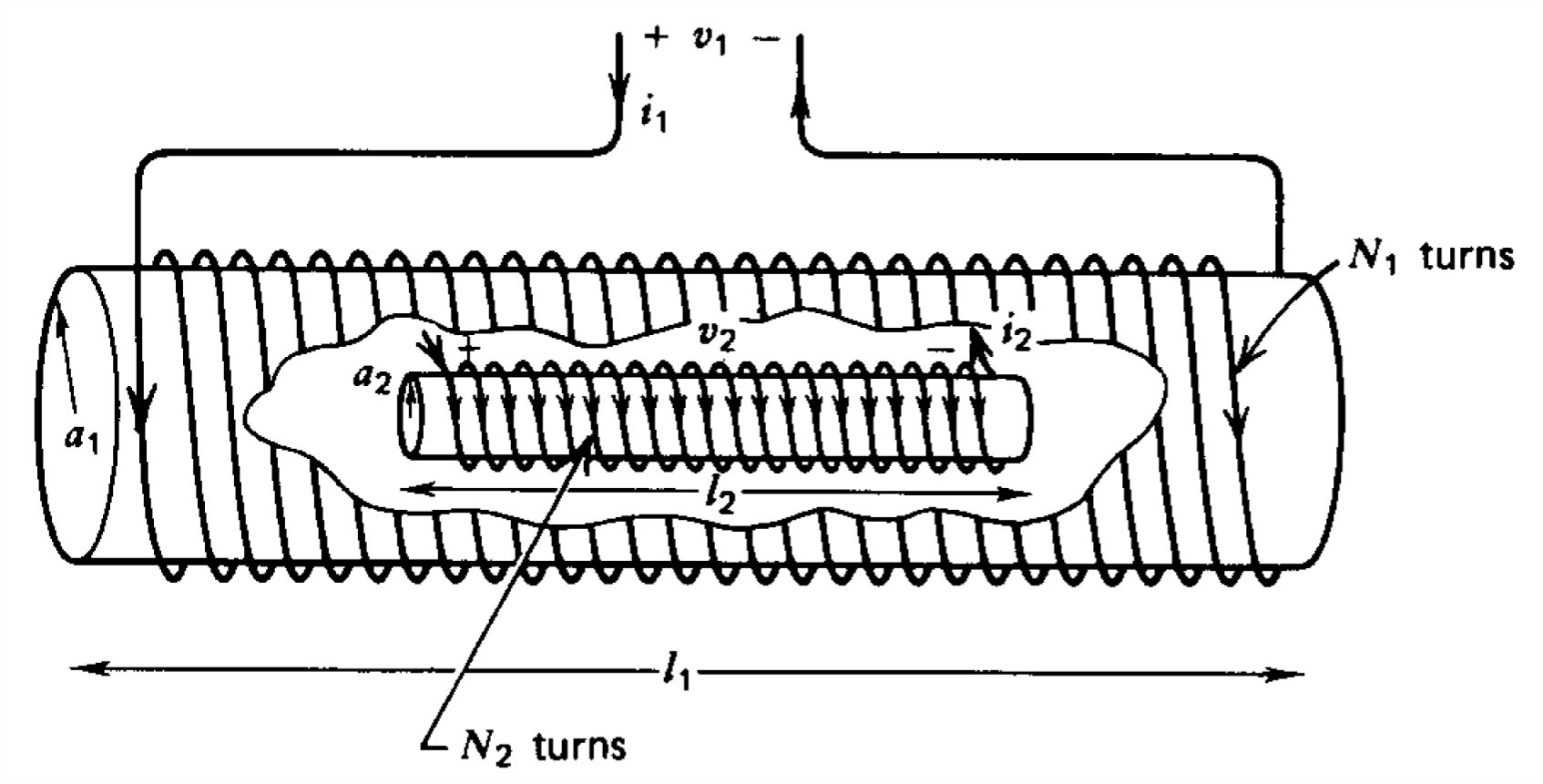
(a) Neglecting fringing field effects find the self-inductances and mutual inductances of each coil. (Hint: Assume the magnetic field is essentially uniform within the cylinders.)
(b) What is the voltage across each coil in terms of \(i_1\) and \(i_{2}\)?
(c) If the coils are connected in series so that \(i_1=i_2\) with the fluxes of each coil in the same direction, what is the total self-inductance?
(d) Repeat (c) if the series connection is reversed so that \(i_1=-i_2\) and the fluxes due to each coil are in opposite directions.
(e) What is the total self-inductance if the coils are connected in parallel so that \(v_1=v_2\) or \(v_1=-v_2\)?
The iron core shown with infinite permeability has three gaps filled with different permeable materials.
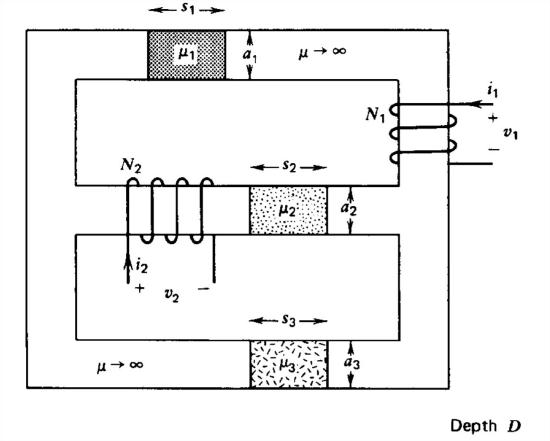
(a) What is the equivalent magnetic circuit?
(b) Find the magnetic flux everywhere in terms of the gap reluctances.
(c) What is the total magnetic flux through each winding?
(d) What is the self-inductance and mutual inductance of each winding?
A cylindrical shell of infinite permeability, length \(l\) and inner radius \(b\) coaxially surrounds a solid cylinder also with infinite permeability and length \(l\) but with smaller radius a so that there is a small gap \(g=b-a\). An \(N_{1}\) turn coil carrying a current \(I_{1}\) is placed within two slots on the inner surface of the outer cylinder.
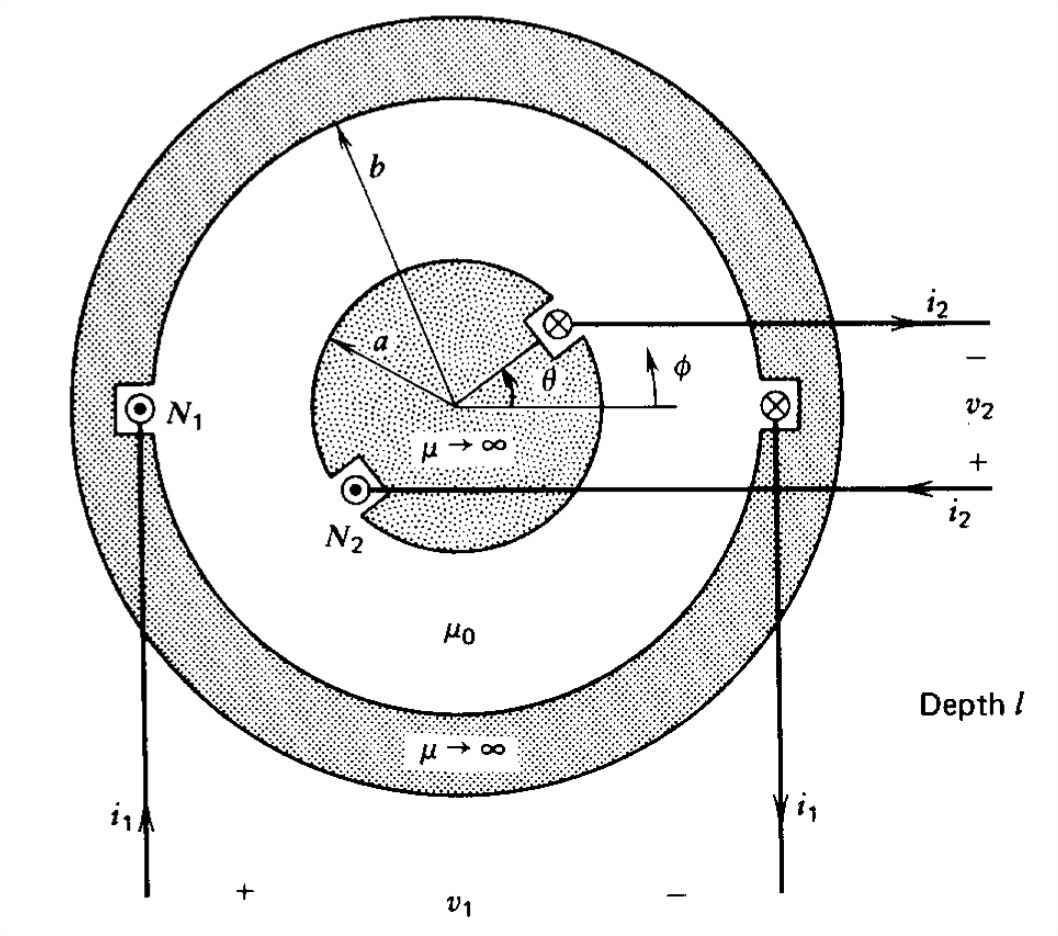
(a) What is the magnetic field everywhere? Neglect all radial variations in the narrow air gap. (Hint: Separately consider \(0< \phi < \pi \) and \(\pi < \phi < 2\pi \).)
(b) What is the self-inductance of the coil?
(c) A second coil with \(N_{2}\) turns carrying a current \(I_{2}\) is placed in slots on the inner cylinder that is free to rotate. When the rotor is at angle \(\theta \) what is the total magnetic field due to currents \(I_{1}\) and \(I_{2}\)? (Hint: Separately consider \(0< \phi < \theta \), \(\theta < \phi < \pi \), \(\pi < \phi < \pi +\theta \), and \(\pi +\theta < \phi < 2\pi \).)
(d) What is the self-inductance and mutual inductance of coil \(2\) as a function of \(\theta \)?
(e) What is the torque on the rotor coil?
(a) What is the ratio of terminal voltages and currents for the odd twisted ideal transformer shown?
(b) A resistor \(R_{L}\) is placed across the secondary winding \(\left ( v_{2},i_{2} \right )\). What is the impedance as seen by the primary winding?

An \(N\) turn coil is wound onto an infinitely permeable magnetic core. An autotransformer is formed by connecting a tap of \(N'\) turns.
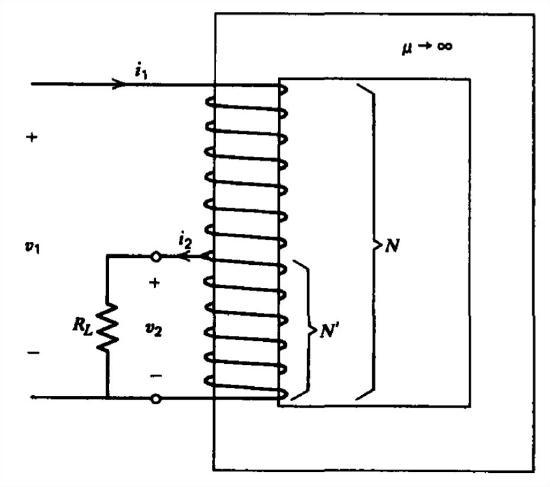
(a) What are the terminal voltage \(\left ( v_{2}/v_{2} \right )\) and current \(\left ( i_{2}/i_{2} \right )\) ratios?
(b) A load resistor \(R_L\) is connected across the terminals of the tap. What is the impedance as seen by the input terminals?
Section 6-3
A conducting material with current density \(J_{x}\textbf{i}_{x}\) has two species of charge carriers with respective mobilities \(\mu _{+}\) and \(\mu _{-}\) and number densities \(n_{+}\) and \(n_{-}\). A magnetic field \(B_{0}\textbf{i}_{z}\) is imposed perpendicular to the current flow.
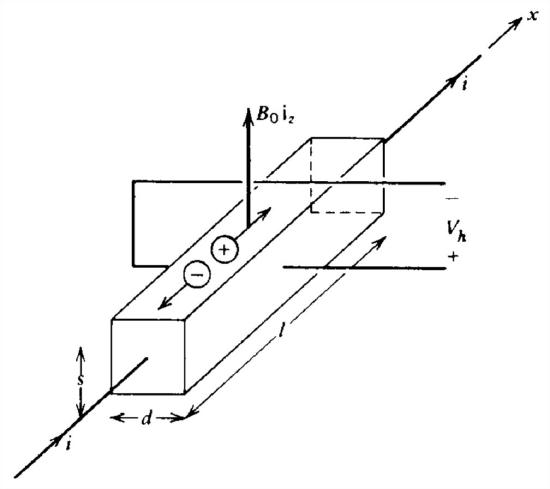
(a) What is the open circuit Hall voltage? (Hint: The transverse current of each carrier must be zero.)
(b) What is the short circuit Hall current?
A highly conducting hollow iron cylinder with permeability \(\mu \) and inner and outer radii \(R_{1}\) and \(R_{2}\) is concentric to an infinitely long dc line current (adapted from L.V. Bewley, Flux Linkages and Electromagnetic Induction. Macmillan, New York, 1952, pp. 71-77).
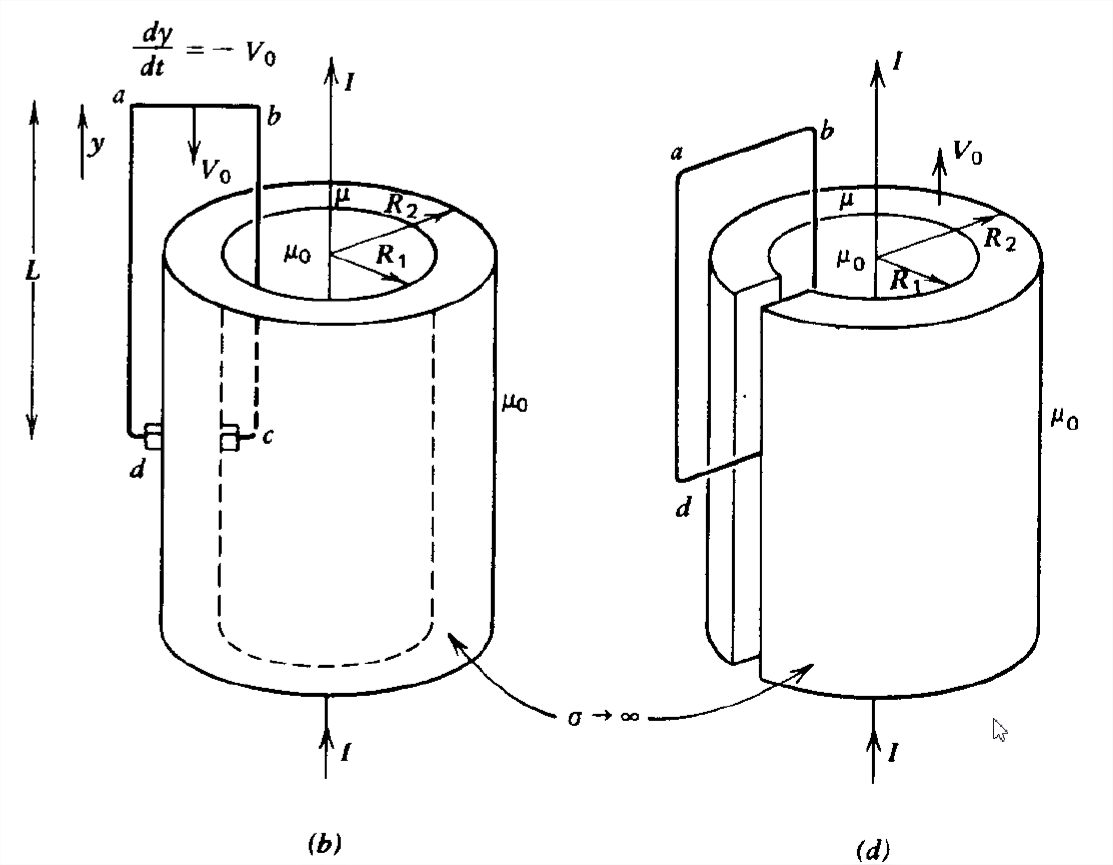
(a) What is the magnetic flux density everywhere? Find the electromotive force \((EMF)\) of the loop for each of the follow ing cases.
(b) A highly conducting circuit \(abcd\) is moving downward with constant velocity \(V_{0}\) making contact with the surfaces of the cylinders via sliding brushes. The circuit is completed from \(c\) to \(d\) via the iron cylinder.
(c) Now the circuit remains stationary and the iron cylinder moves upwards at velocity \(V_{0}\).
(d) Now a thin axial slot is cut in the cylinder so that it can slip by the complete circuit \(abcd\), which remains stationary as the cylinder moves upwards at speed \(V_{0}\). The brushes are removed and a highly conducting wire completes the \(c-d\) path.
A very long permanently magnetized cylinder \(M_{0}\textbf{i}_{z}\) rotates on a shaft at constant angular speed \(\omega \). The inner and outer surfaces at \(\textrm{r}=a\) and \(\textrm{r}=b\) are perfectly conducting, so that brushes can make electrical contact.
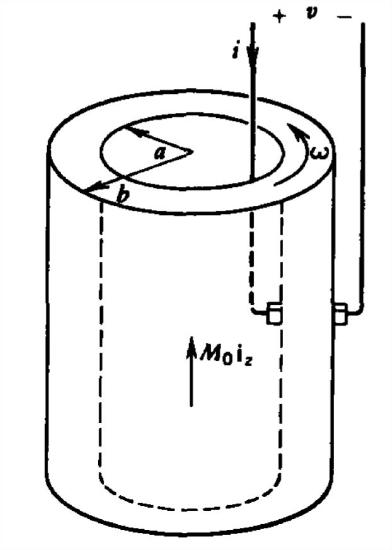
(a) If the cylinder is assumed very long compared to its radius, what are the approximate values of \(\textbf{B}\) and \(\textbf{H}\) in the magnet?
(b) What is the open circuit voltage?
(c) If the magnet has an Ohmic conductivity \(\sigma \), what is the equivalent circuit of this generator?
(d) What torque is required to turn the magnet if the terminals are short circuited?
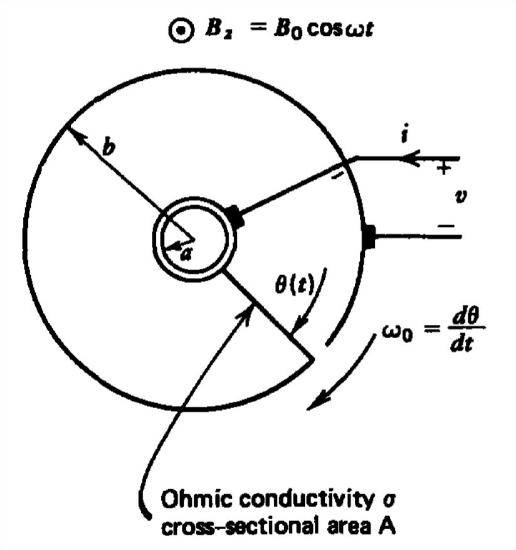
A single spoke wheel has a perfectly conducting cut rim. The spoke has Ohmic conductivity \(\sigma \) and cross-sectional area \(A\). The wheel rotates at constant angular speed \(\omega _{0}\) in a sinusoidally varying magnetic field \(B_{z}=B_{0}\cos \omega t\).
(a) What is the open circuit voltage and short circuit current?
(b) What is the equivalent circuit?
An \(\textrm{MHD}\) machine is placed within a magnetic circuit.
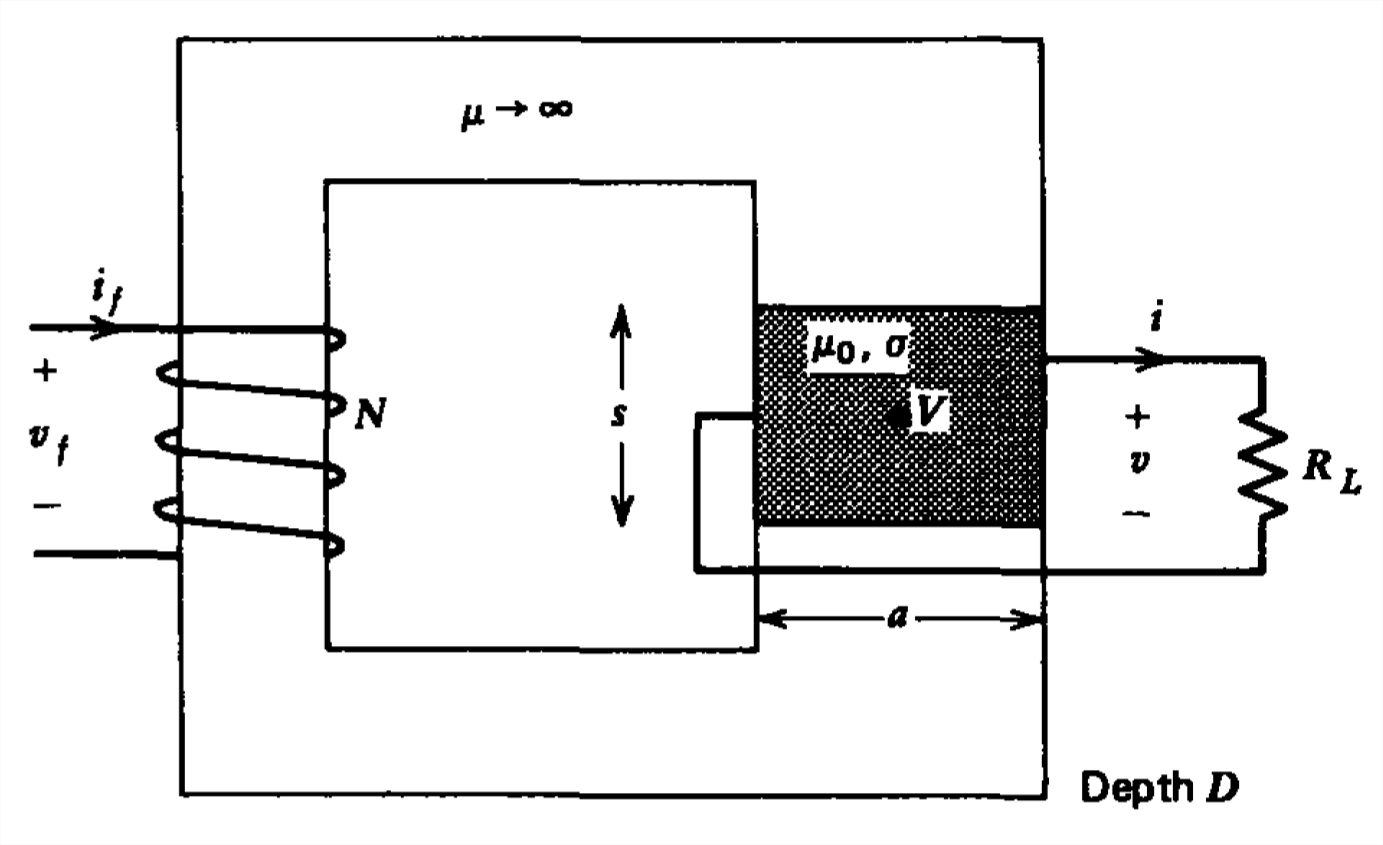
(a) A constant dc current \(i_{f}=I_{0}\) is applied to the \(N\) turn coil. How much power is delivered to the load resistor \(R_L\)?
(b) The \(\textrm{MHD}\) machine and load resistor \(R_L\) are now connected in series with the \(N\) turn coil that has a resistance \(R_f\). No current is applied. For what minimum flow speed can the \(\textrm{MHD}\) machine be self-excited?
The field winding of a homopolar generator is connected in series with the rotor terminals through a capacitor \(C\). The rotor is turned at constant speed \(\omega \).
(a) For what minimum value of rotor speed is the system self-excited?
(b) For the self-excited condition of (a) what range of values of \(C\) will result in dc self-excitation or in ac self-excitation?
(c) What is the frequency for ac self-excitation?

Section 6-4
An Ohmic block separates two perfectly conducting parallel plates. A dc current that has been applied for a long time is instantaneously turned off at \(t =0\).
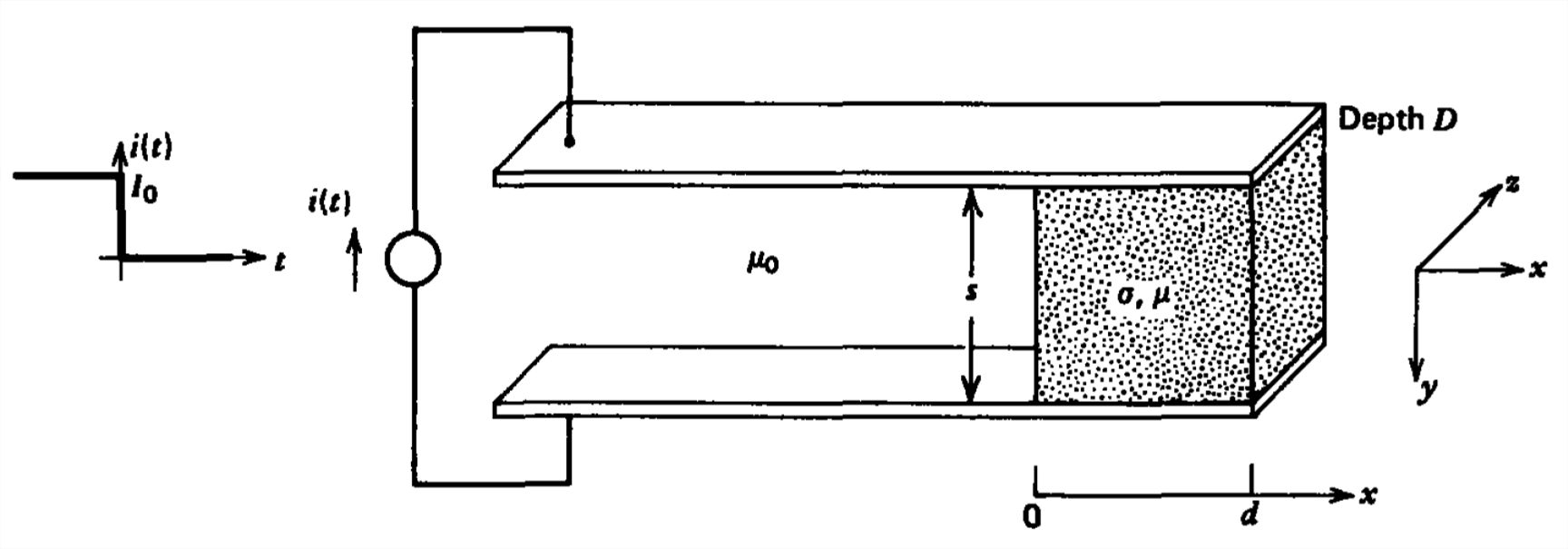
(a) What are the initial and final magnetic field distributions? What are the boundary conditions?
(b) What are the transient magnetic field and current distributions?
(c) What is the force on the block as a function of time?
A block of Ohmic material is placed within a magnetic circuit. A step current \(I_{0}\) is applied at \(t =0\).
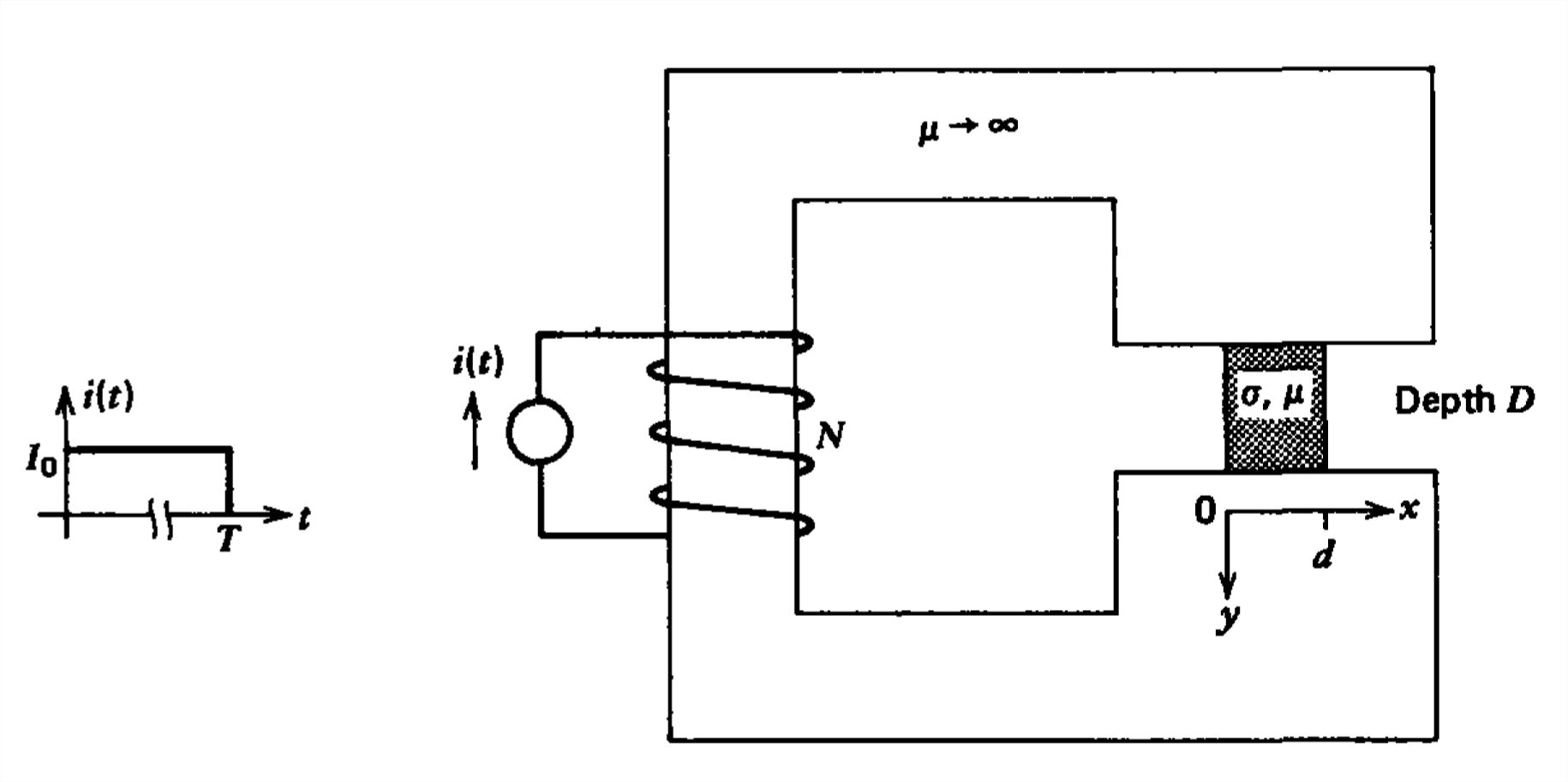
(a) What is the dc steady-state solution for the magnetic field distribution?
(b) What are the boundary and initial conditions for the magnetic field in the conducting block?
(c) What are the transient field and current distributions?
(d) What is the time dependence of the force on the conductor?
(e) The current has been on a long time so that the system is in the dc steady state found in (a) when at \(t = T\) the current is instantaneously turned off. What are the transient field and current distributions in the conductor?
(f) If the applied coil current varies sinusoidally with time as \(i\left ( t \right )=I_{0}\cos \omega t\), what are the sinusoidal steady-state field and current distributions? (Hint: Leave your answer in terms of complex amplitudes.)
(g) What is the force on the block?
A semi-infinite conducting block is placed between parallel perfect conductors. A sinusoidal current source is applied.

(a) What are the magnetic field and current distributions within the conducting block?
(b) What is the total force on the block?
(c) Repeat (a) and (b) if the block has length \(d\).
A current sheet that is turned on at \(t =0\) lies a distance \(d\) above a conductor of thickness \(D\) and conductivity \(\sigma \). The conductor lies on top of a perfectly conducting plane.
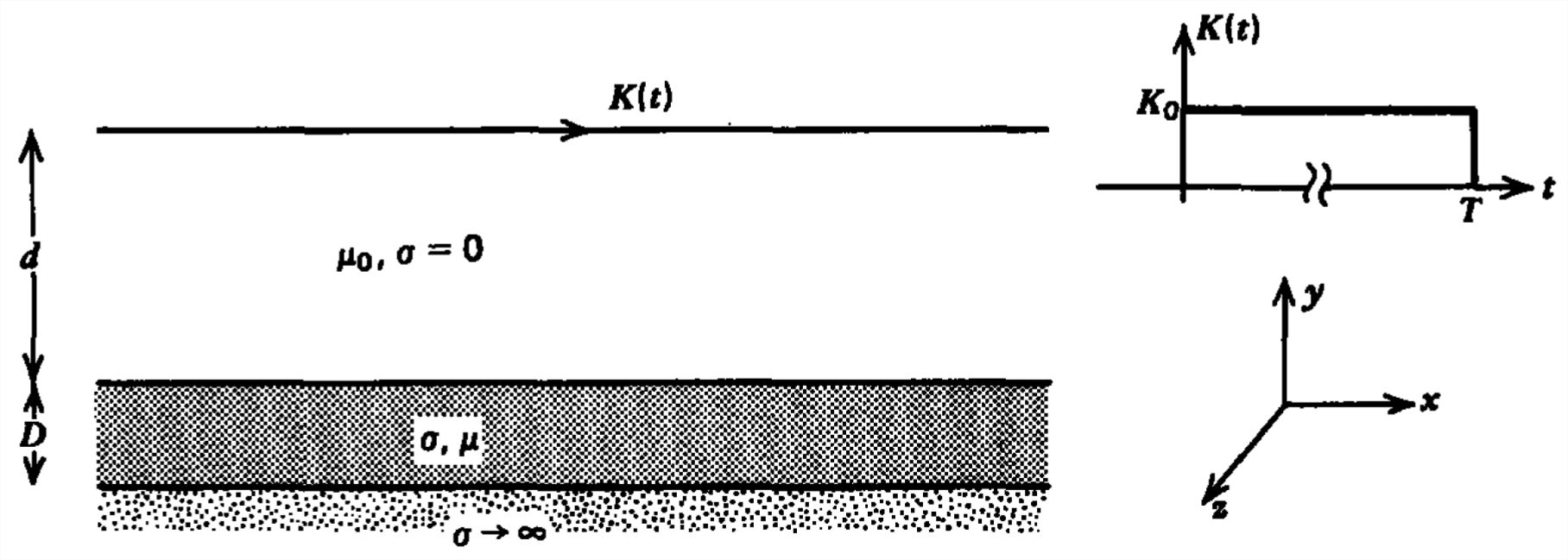
(a) What are the initial and steady-state solutions? What are the boundary conditions?
(b) What are the transient magnetic field and current distributions?
(c) After a long time \(T\), so that the system has reached the dc steady state, the surface current is set to zero. What are the subsequent field and current distributions?
(d) What are the field and current distributions if the current sheet varies as \(K_{0}\cos \omega t\)?
Distributed dc currents at \(x =0\) and \(x = l\) flow through a conducting fluid moving with constant velocity \(v_{0}\textbf{i}_{x}\).
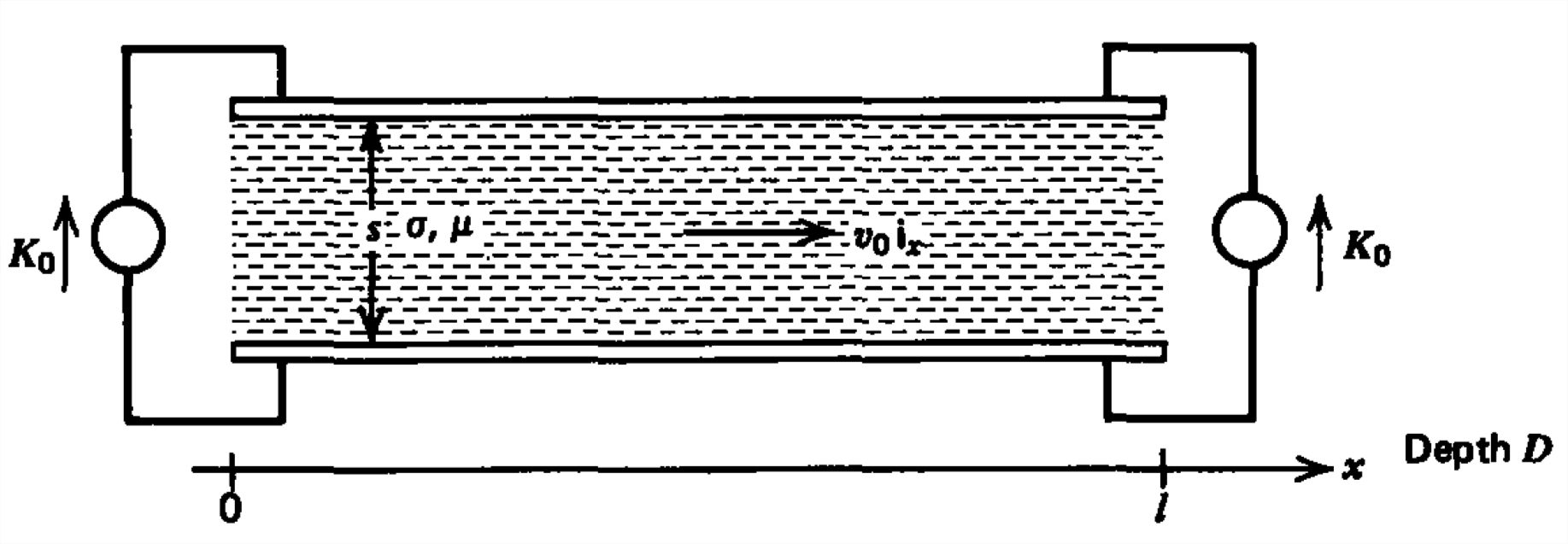
(a) What are the magnetic field and current distributions?
(b) What is the force on the fluid?
A sinusoidal surface current at \(x =0\) flows along parallel electrodes and returns through a conducting fluid moving to the right with constant velocity \(v_{0}\textbf{i}_{x}\). The flow is not impeded by the current source. The system extends to \(x=\infty \).
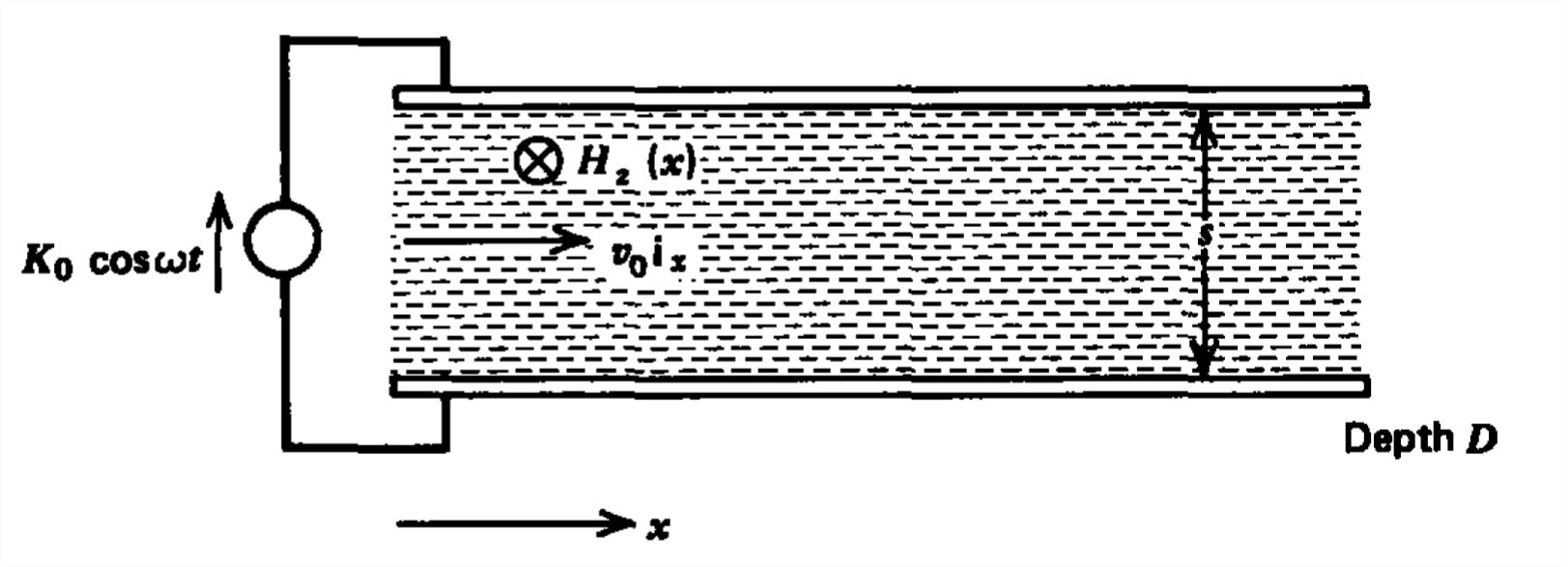
(a) What are the magnetic field and current density dis tributions?
(b) What is the time-average force on the fluid?
The surface current for the linear induction machine treated in Section 6-4-6 is now put a distance \(s\) below the conductor.
(a) What are the magnetic field and current distributions in each region of space? (Hint: Check your answer with Section 6-4-6 when \(s=0\).)
(b) Repeat (a) if \(s\) is set to zero but the conductor has a finite thickness \(d\).
A superconducting block with plasma frequency \(\omega_{p}\), is placed within a magnetic circuit with exciting current \(I_{0}\cos \omega t\).
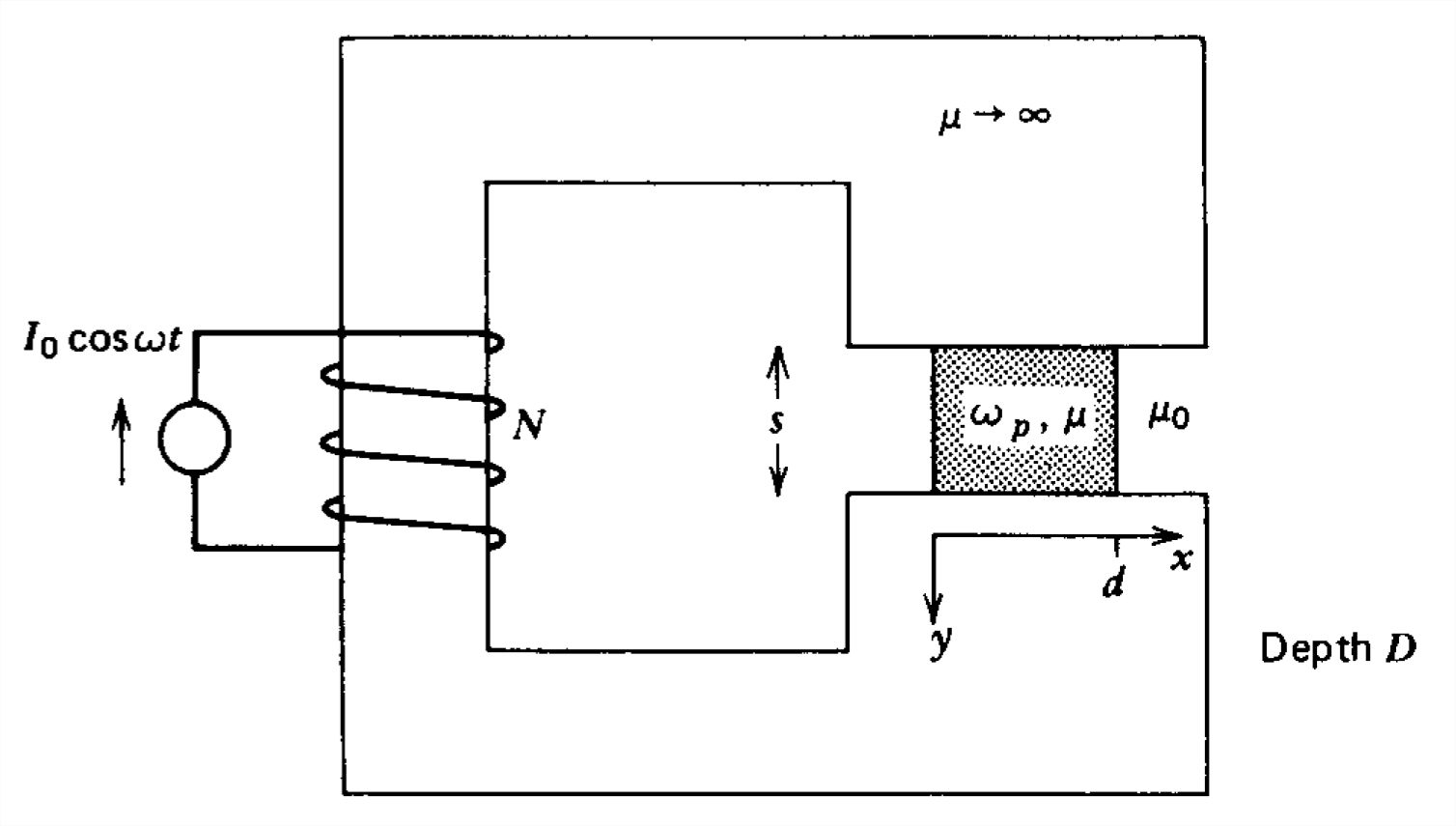
(a) What are the magnetic field and current distributions in the superconductor?
(b) What is the force on the block?
Section 6.5
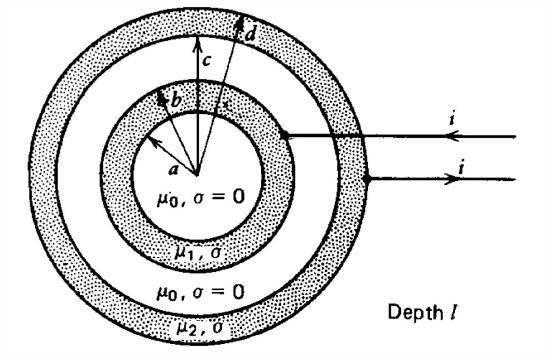
Find the magnetic energy stored and the self-inductance for the geometry below where the current in each shell is uniformly distributed.
Find the external self-inductance of the two wire lines shown. (Hint: See Section 2-6-4c.)

A coaxial cable with solid inner conductor is excited by a sinusoidally varying current \(I_{0}\cos \omega t\) at high enough frequency so that the skin depth is small compared to the radius \(a\). The current is now nonuniformly distributed over the inner conductor.
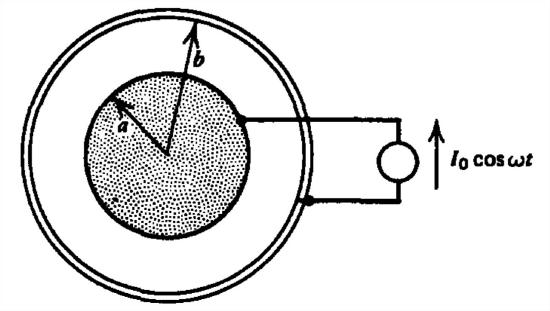
(a) Assuming that \(\textbf{H}=H_{\phi }\left ( \textrm{r} \right )\textbf{i}_{\phi }\), what is the governing equation for \(H_{\phi }\left ( \textrm{r} \right )\) within the inner cylinder. (Hint: \(\nabla^{2}\textbf{H}=\nabla\left ( \nabla \underset{\nearrow \quad }{\overset{\qquad 0}{\overset{\quad \nearrow}{\cdot}}} \textbf{H} \right )-\nabla\times \left ( \nabla\times \textbf{H} \right )\))
(b) Solve (a) for solutions of the form
\(H_{\phi }\left ( \textrm{r} \right )=\textrm{Re}\left [ \hat{H}_{\phi }\left ( \textrm{r} \right )e^{j\omega t} \right ]\)
Hint: Bessel's equation is
\(x^{2}\frac{d^{2}y}{dx^{2}}+x\frac{dy}{dx}+\left ( x^{2}-p^{2} \right )y=0\)
with solutions
\(y=A_{1}J_{p}\left ( x \right )+A_{2}Y_{p}\left ( x \right )\)
where \(Y_{p}\) is singular at \(x=0\).
(c) What is the current distribution? Hint:
\(\frac{d}{dx}\left [ J_{1}\left ( x \right ) \right ]+\frac{1}{x} J_{1}\left ( x \right )=J_{0}\left ( x \right )\)
Section 6-6
A reluctance motor is made by placing a high permeability material, which is free to rotate, in the air gap of a magnetic circuit excited by a sinusoidal current \(I_{0}\cos \omega _{0}t\).
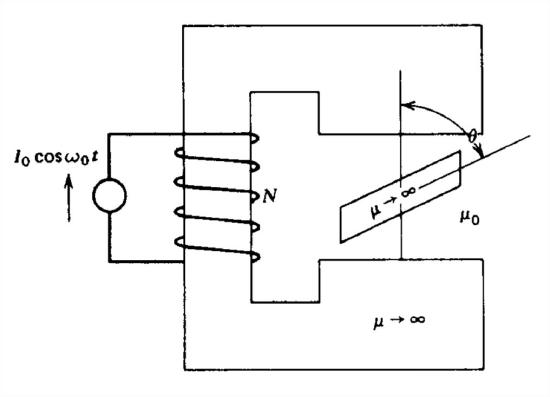
The inductance of the circuit varies as
\(L\left ( \theta \right )=L_{0}+L_{1}\cos 2\theta \)
where the maximum inductance \(L_{0}+L_{1}\) occurs when \(\theta =0\) or \(0=\pi \) and the minimum inductance \(L_{0}-L_{1}\) occurs when \(0=\pm \pi /2\)
(a) What is the torque on the slab as a function of the angle \(\theta\)?
(b) The rotor is rotating at constant speed \(\omega \), where \(\theta =\omega t+\delta \) and \(\delta \) is the angle of the rotor at \(t = 0\). At what value of \(\omega \) does the torque have a nonzero time average. The reluctance motor is then a synchronous machine. Hint:
\(\begin{align} \cos ^{2}\omega _{0}t\sin 2\theta &=\frac{1}{2}\left [ \sin 2\theta +\cos 2\omega _{0}t\sin 2\theta \right ] \\ &
=\frac{1}{2}\left \{ \sin 2\theta+\frac{1}{2}\left [ \sin 2\left ( \omega _{0}t+\theta \right )+\sin 2\left ( \theta -\omega _{0}t \right ) \right ] \right \} \end{align}\)
(c) What is the maximum torque that can be delivered by the shaft and at what angle \(\delta \) does it occur?
A system of two coupled coils have the following flux-current relations:
\(\Phi _{1}=L_{1}\left ( \theta \right )i_{1}+M\left ( \theta \right )i_{2}\\
\Phi _{2}=M\left ( \theta \right )i_{1}+L_{2}\left ( \theta \right )i_{2}\)
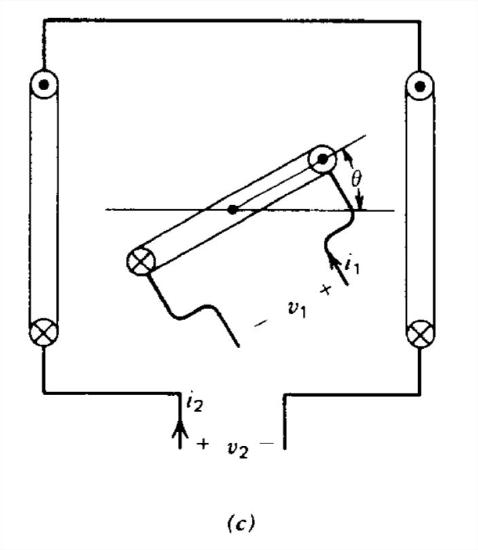
(a) What is the power \(p\) delivered to the coils?
(b) Write this power in the form
\(p=\frac{dW}{dt}+T\frac{d\theta }{dt}\)
What are \(W\) and \(T\)?
(c) A small coil is free to rotate in the uniform magnetic field produced by another coil. The flux-current relation is
\(\Phi _{1}=L_{1}i_{1}+M_{0}i_{2}\sin \theta \\
\Phi _{2}=M_{0}i_{1}\sin \theta +L_{2}i_{2} \)
The coils are excited by dc currents \(I_{1}\) and \(I_{2}\). What is the torque on the small coil?
(d) If the small coil has conductivity \(\sigma \), cross-sectional area \(A\), total length \(l\), and is short circuited, what differential equation must the current \(i_{1}\) obey if \(\theta \) is a function of time? A dc current \(I_{2}\) is imposed in coil \(2\).
(e) The small coil has moment of inertia \(J\). Consider only small motions around \(\theta =0\) so that \(\cos \theta \approx 1\). With the torque and current equations linearized, try exponential solutions of the form \(e^{st}\) and solve for the natural frequencies.
(f) The coil is released from rest at \(\theta =\theta _{0}\). What is \(\theta \left ( t \right )\) and \(i_{1}\left ( t \right )\)? Under what conditions are the solutions oscillatory? Damped?
A coaxial cable has its short circuited end free to move.
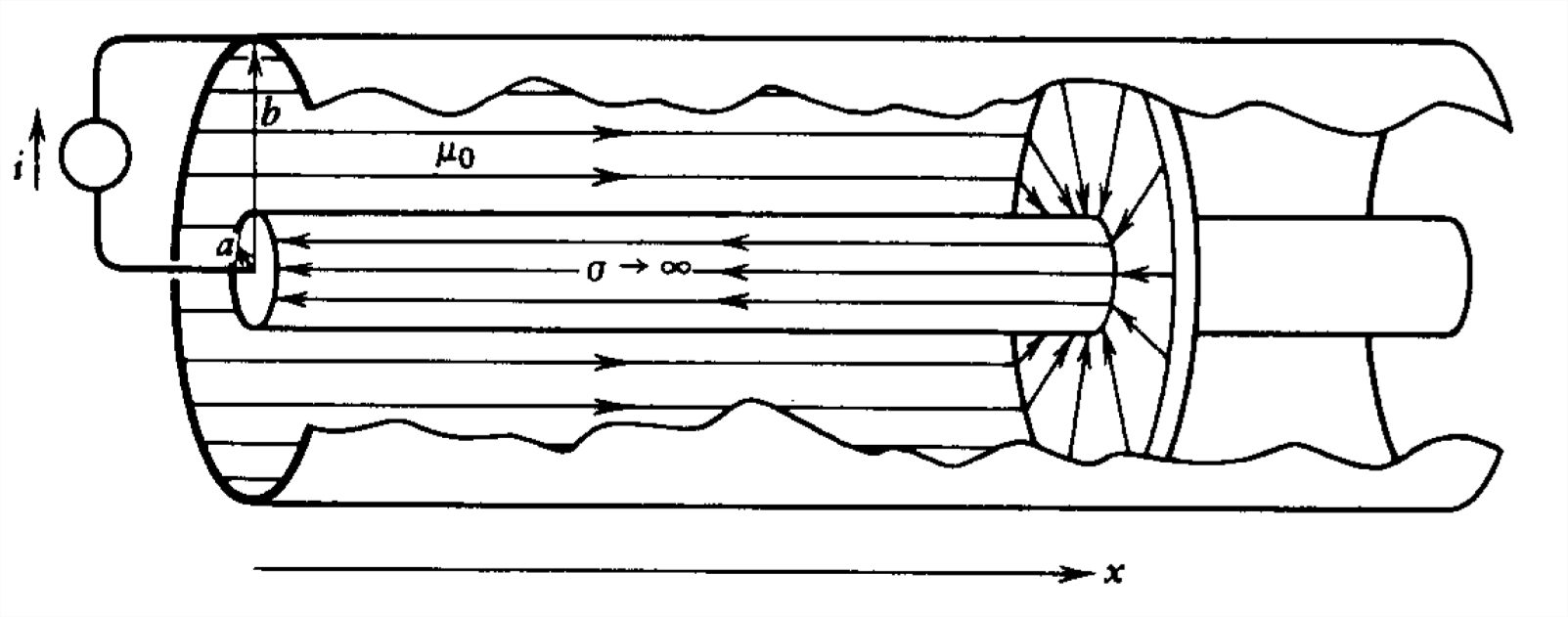
(a) What is the inductance of the cable as a function of \(x\)?
(b) What is the force on the end?
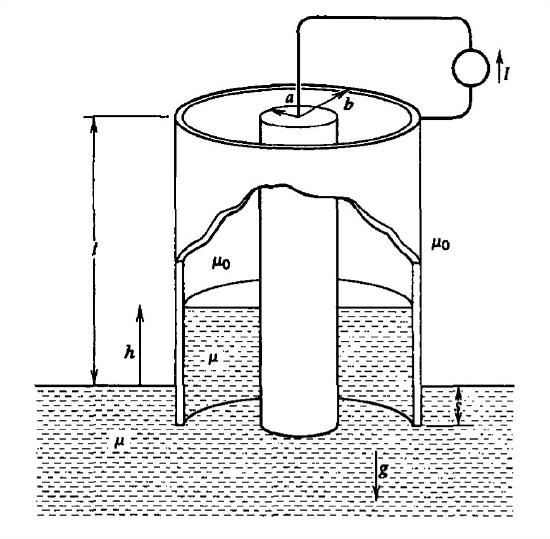
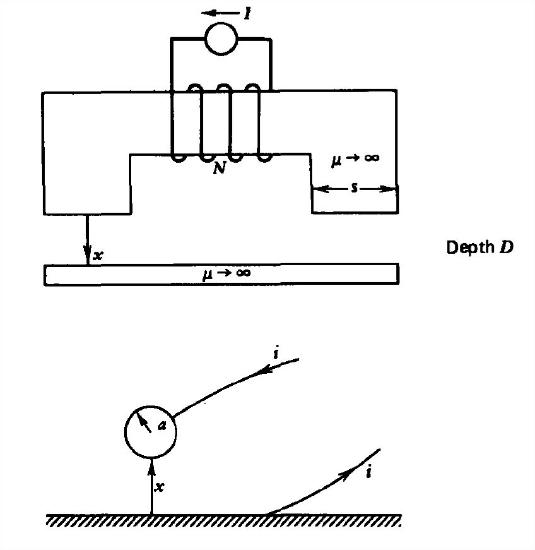
For the following geometries, find:
(a) The inductance;
(b) The force on the moveable member.
A coaxial cylinder is dipped into a magnetizable fluid with permeability \(\mu \) and mass density \(\rho _{m}\). How high \(h\) does the fluid rise within the cylinder?