7.11: Problems
- Page ID
- 83358
Section 7-1
For the following electric fields in a linear media of permittivity \(\varepsilon \) and permeability \(\mu \) find the charge density, magnetic field, and current density.
(a) \(\textbf{E}=E_{0}\left ( x\textbf{i}_{x}+y\textbf{i}_{y} \right )\sin \omega t\)
(b) \(\textbf{E}=E_{0}\left ( y\textbf{i}_{x}-x\textbf{i}_{y} \right )\cos \omega t\)
(c) \(\textbf{E}=\textrm{Re}\left [E_{0}e^{j\left ( \omega t-k_{x}x-k_{z}z \right )} \textbf{i}_{y}\right ]\). How must \(k_{x}\), \(k_{z}\) and \(\omega \) be related so that \(\textbf{J}=0\)?
An Ohmic conductor of arbitrary shape has an initial charge distribution \(\rho _{0}\left ( \textbf{r} \right )\) at \(t=0\).
(a) What is the charge distribution for all time?
(b) The initial charge distribution is uniform and is confined between parallel plate electrodes of spacing \(d\). What are the electric and magnetic fields when the electrodes are opened or short circuited?
(c) Repeat (b) for coaxial cylindrical electrodes of inner radius \(a\) and outer radius \(b\).
(d) When does a time varying electric field not generate a magnetic field
(a) For linear media of permittivity \(\varepsilon \) and permeability \(\mu \), use the magnetic vector potential \(\textbf{A}\) to rewrite Faraday's law as the curl of a function.
(b) Can a scalar potential function \(V\) be defined? What is the electric field in terms of \(V\) and \(\textbf{A}\)? The choice of \(V\) is not unique so pick \(V\) so that under static conditions \(\textbf{E}=-\nabla V\).
(c) Use the results of (a) and (b) in Ampere's law with Maxwell's displacement current correction to obtain a single equation in \(\textbf{A}\) and \(V\). (Hint: \(\nabla\times \left ( \nabla\times \textbf{A} \right )=\nabla\left ( \nabla\cdot \textbf{A}-\nabla^{2} \textbf{A} \right )\))
(d) Since we are free to specify \(\nabla\cdot \textbf{A}\), what value should we pick to make (c) an equation just in \(\textbf{A}\)? This is called setting the gauge.
(e) Use the results of (a)-(d) in Gauss's law for \(\textbf{D}\) to obtain a single equation in \(V\).
(f) Consider a sinusoidally varying point charge at \(r=0\), \(\hat{\mathcal{Q}}e^{j\omega t}\). Solve (e) for \(r >0\).
Hint:
\(\frac{1}{r}\frac{\partial }{\partial r}\left ( r^{2}\frac{\partial V}{\partial r} \right )=\frac{\partial^2 }{\partial r^2}\left ( rV \right )\)
Define a new variable \(\left ( rV \right )\). By symmetry, \(V\) only depends on \(r\) and waves can only propagate away from the charge and not towards it. As \(r\rightarrow 0\), the potential approaches the quasi-static Coulomb potential.
Section 7-2
Poynting's theorem must be modified if we have a hysteretic material with a nonlinear and double-valued relationship between the polarization \(\textbf{P}\) and electric field \(\textbf{E}\) and the magnetization \(\textbf{M}\) and magnetic field \(\textbf{H}\).
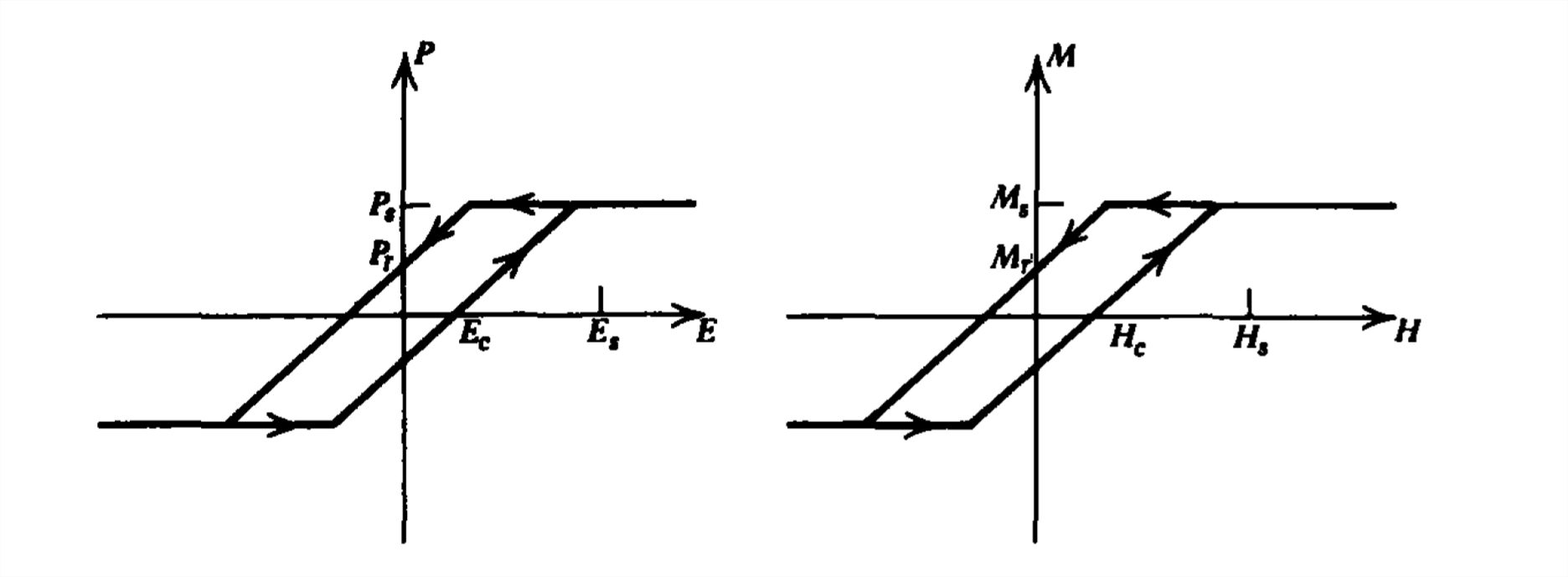
(a) For these nonlinear constitutive laws put Poynting's theorem in the form
\(\nabla \cdot \textbf{S}+\frac{\partial w}{\partial t}=-P_{d}-P_{p}-P_{M}\)
where \(P_{d}\) and \(P_{M}\) are the power densities necessary to polarize and magnetize the material.
(b) Sinusoidal electric and magnetic fields \(\textbf{E}=\textbf{E}_{s}\cos \omega t\) and \(\textbf{H}=\textbf{H}_{s}\cos \omega t\) are applied. How much energy density is dissipated per cycle?
An electromagnetic field is present within a superconductor with constituent relation
\(\frac{\partial \textbf{J}_{f}}{\partial t}=\omega_{p}^{2}\varepsilon \textbf{E}\)
(a) Show that Poynting's theorem can be written in the form
\(\nabla \cdot \textbf{S}+\frac{\partial w}{\partial t}=0\)
What is \(w\)?
(b) What is the velocity of the charge carriers each with charge \(q\) in terms of the current density \(\textbf{J}_{f}\)? The number density of charge carriers is \(n\).
(c) What kind of energy does the superconductor add?
(d) Rewrite Maxwell's equations with this constitutive law for fields that vary sinusoidally with time.
(e) Derive the complex Poynting theorem in the form
\(\nabla \cdot \left [ \frac{1}{2}\hat{\textbf{E}}\left ( \textbf{r} \right )\times \hat{\textbf{H}}^{\ast }\left ( \textbf{r} \right ) \right ]+2jw<w>=0\)
What is \(<w>\)?
A paradoxical case of Poynting's theorem occurs when a static electric field is applied perpendicularly to a static magnetic field, as in the case of a pair of electrodes placed within a magnetic circuit.
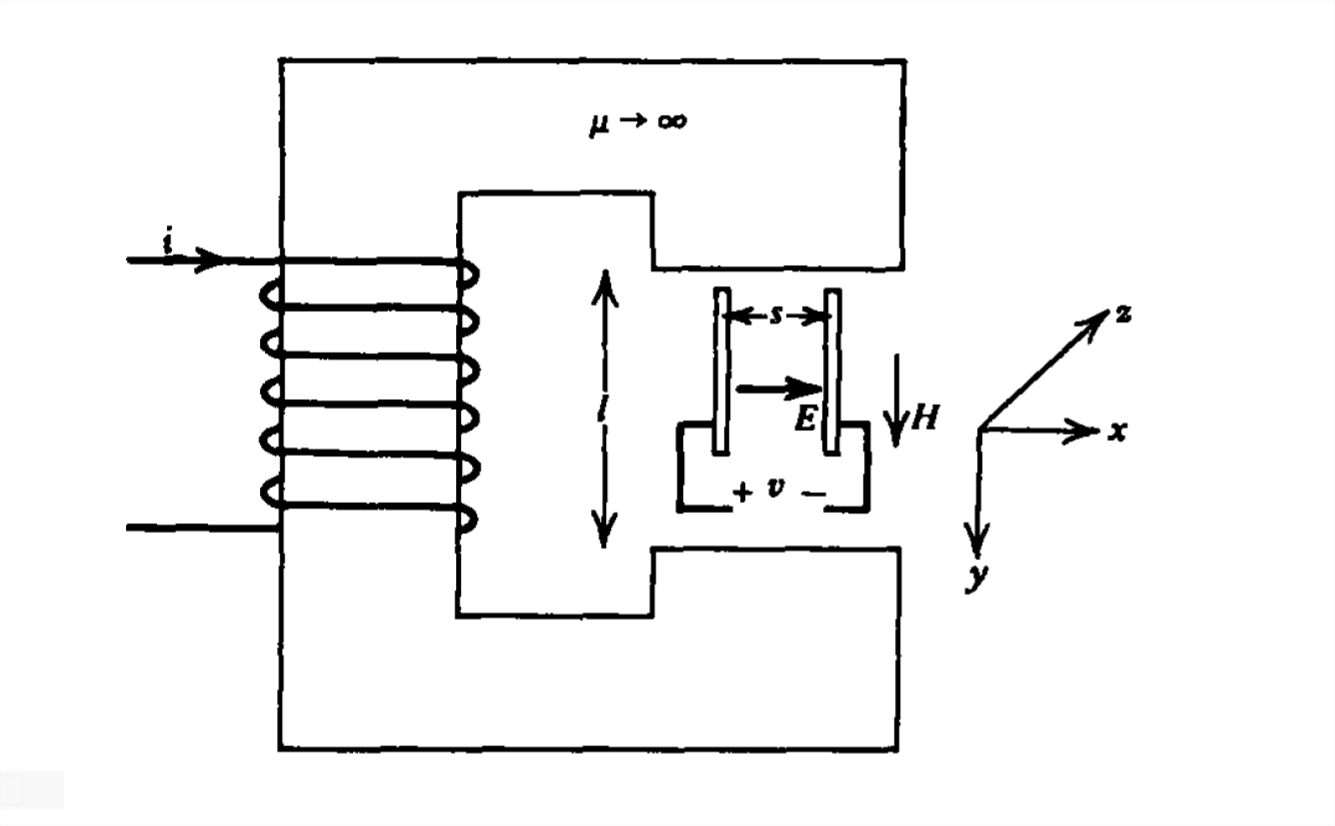
(a) What are \(\textbf{E}\), \(\textbf{H}\), and \(\textbf{S}\)?
(b) What is the energy density stored in the system?
(c) Verify Poynting's theorem.
The complex electric field amplitude has real and imaginary parts
\(\hat{\textbf{E}}\left ( \textbf{r} \right )=\textbf{E}_{r}+j\textbf{E}_{i}\)
Under what conditions are the following scalar and vector products zero:
(a) \(\hat{\textbf{E}}\cdot \hat{\textbf{E}}\overset{?}{=}0\)
(b) \(\hat{\textbf{E}}\cdot \hat{\textbf{E}}^{\ast }\overset{?}{=}0\)
(c) \(\hat{\textbf{E}}\times \hat{\textbf{E}}\overset{?}{=}0\)
(d) \(\hat{\textbf{E}}\times \hat{\textbf{E}}^{\ast }\overset{?}{=}0\)
Section 7.3
Consider a lossy medium of permittivity \(\varepsilon \), permeability \(\mu \), and Ohmic conductivity \(\sigma \).
(a) Write down the field equations for an \(x\)-directed electric field.
(b) Obtain a single equation in \(E_x\).
(c) If the fields vary sinusoidally with time,
\(E_{x}=\textrm{Re}\left [ \hat{E}_{x}\left ( z \right )e^{j\omega t} \right ]\)
what are the spatial dependences of the fields?
(d) Specialize (c) to the (i) low loss limit \(\left ( \sigma /\omega \varepsilon \ll 1 \right )\) and (ii) large loss limit \(\left ( \sigma /\omega \varepsilon \gg 1 \right )\).
(e) Repeat (a)-(c) if the medium is a plasma with constitutive law
\(\frac{\partial \textbf{J}}{\partial t}=\omega _{p}^{2}\varepsilon \textbf{E}\)
(f) A current sheet \(K_{0}\cos \omega t\textbf{i}_{x}\) is placed at \(z = 0\). Find the electric and magnetic fields if the sheet is placed within an Ohmic conductor or within a plasma.
9. A uniformly distributed volume current of thickness \(2d\), \(J_{0}\cos wt\textbf{i}_{x}\), is a source of plane waves.
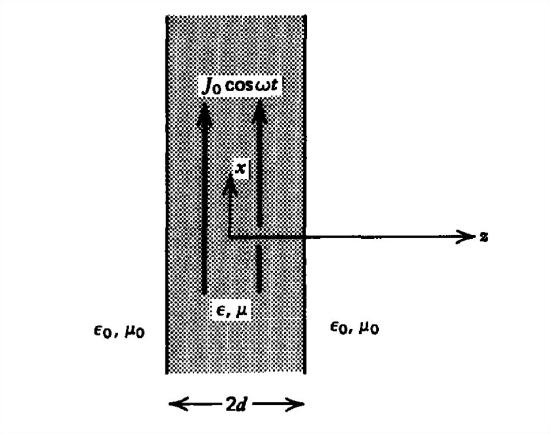
(a) From Maxwell's equations obtain a single differential equation relating \(E_{x}\) to \(J_{x}\).
(b) Find the electric and magnetic fields within and outside the current distribution.
(c) How much time-average power per unit area is delivered by the current?
(d) How does this generated power compare to the electromagnetic time-average power per unit area leaving the volume current at \(z=\pm d\)?
A TEM wave \(\left ( E_{x},H_{y} \right )\) propagates in a medium whose permittivity and permeability are functions of \(z\), \(\varepsilon \left ( z \right )\), and \(\mu \left ( z \right )\).
(a) Write down Maxwell's equations and obtain single partial differential equations in \(E_{x}\) and \(H_{y}\).
(b) Consider the idealized case where \(\varepsilon \left ( z \right )=\varepsilon e^{\alpha \left | z \right |}\) and \(\mu \left ( z \right )=\mu e^{-\alpha \left | z \right |}\). A current sheet \(K_{0}e^{j\omega t}\textbf{i}_{x}\) is at \(z=0\). What are the resulting electric and magnetic fields on each side of the sheet?
(c) For what values of a are the solutions spatially evanescent or oscillatory?
We wish to compare various measurements between two observers, the second moving at a constant velocity \(v\textbf{i}_{z}\), with respect to the first.
(a) The first observer measures simultaneous events at two positions \(z_{1}\) and \(z_{2}\) so that \(t_{1}=t_{2}\). What is the time interval between the two events \(t_{1}'-t_{2}'\) as measured by the second observer?
(b) The first observer measures a time interval \(\Delta t=t_{1}-t_{2}\) between two events at the same position \(z\). What is the time interval as measured by the second observer?
(c) The first observer measures the length of a stick as \(L=z_{2}-z_{1}\). What is the length of the stick as measured by the second observer?
A stationary observer measures the velocity of a particle as \(\textbf{u}=u_{x}\textbf{i}_{x}+u_{y}\textbf{i}_{y}+u_{z}\textbf{i}_{z}\).
(a) What velocity, \(\textbf{u}'=u_{x}'\textbf{i}_{x}+u_{y}'\textbf{i}_{y}+u_{z}'\textbf{i}_{z}\), does another observer moving at constant speed \(v\textbf{i}_{z}\), measure?
(b) Find \(\textbf{u}'\) for the following values of \(\textbf{u}\) where \(c_0\) is the free space speed of light:
(i) \(\textbf{u}=c_{0}\textbf{i}_{x}\)
(ii) \(\textbf{u}=c_{0}\textbf{i}_{y}\)
(iii) \(\textbf{u}=c_{0}\textbf{i}_{z}\)
(iv) \(\textbf{u}=\left (c_{0} /\sqrt{3} \right )\left [\textbf{i}_{x} +\textbf{i}_{y}+\textbf{i}_{z}\right ]\)
(c) Do the results of (a) and (b) agree with the postulate that the speed of light for all observers is \(c_0\)?
Section 7.4
An electric field is of the form
\(\textbf{E}=100e^{j\left ( 2\pi \times 10^{6}t-2\pi \times 10^{-2}z \right )}\textbf{i}_{x} \, \textrm{volts/m}\)
(a) What is the frequency, wavelength, and speed of light in the medium?
(b) If the medium has permeability \(\mu _{0}=4\pi \times 10^{-7}\,\textrm{henry/m}\), what is the permittivity \(\varepsilon \), wave impedance \(\eta \), and the magnetic field?
(c) How much time-average power per unit area is carried by the wave?
The electric field of an elliptically polarized plane wave in a medium with wave impedance (\eta \) is
\(\textbf{E}=\textrm{Re}\left ( E_{x0}\textbf{i}_{x}+E_{y0}e^{j\phi }\textbf{i}_{y} \right )e^{j\left ( \omega t-kz \right )}\)
where \(E_{x0}\) and \(E_{y0}\) are real.
(a) What is the magnetic field?
(b) What is the instantaneous and time-average power flux densities?
In Section 3-1-4 we found that the force on one of the charges \(\mathcal{Q}\) of a spherical atomic electric dipole of radius \(R_{0}\) is
\(\textbf{F}=\mathcal{Q}\left [ \textbf{E}-\frac{\mathcal{Q}\textbf{d}}{4\pi \varepsilon _{0}R_{0}^{3}} \right ]\)
where \(\textbf{d}\) is the dipole spacing.
(a) Write Newton's law for this moveable charge with mass \(M\) assuming that the electric field varies sinusoidally with time as \(E_{0}\cos \omega t\) and solve for \(\textbf{d}\). (Hint: Let \(\omega _{0}^{2}=\mathcal{Q}^{2}/\left ( M4\pi \varepsilon _{0}R_{0}^{3} \right )\))
(b) What is the polarization \(\textbf{P}\) as a function of \(\textbf{E}\) if there are \(N\) dipoles per unit volume? What is the frequency dependent permittivity function \(\varepsilon \left ( \omega \right )\), where
\(\textbf{D}\left ( \textbf{r} \right )=\varepsilon \left ( \omega \right )\textbf{E}\left ( \textbf{r} \right )\)
This model is often appropriate for light propagating in dielectric media.
(c) Use the results of (b) in Maxwell's equations to find the relation between the wavenumber \(k\) and frequency \(\omega \).
(d) For what frequency ranges do we have propagation or evanescence?
(e) What are the phase and group velocities of the waves?
(f) Derive the complex Poynting's theorem for this dispersive dielectric.
High-frequency wave propagation in the ionosphere is partially described by the development in Section 7-4-4 except that we must include the earth's dc magnetic field, which we take to be \(H_{0}\textbf{i}_{z}\).
(a) The charge carriers have charge \(q\) and mass \(m\). Write the three components of Newton's force law neglecting collisions but including inertia and the Coulomb-Lorentz force law. Neglect the magnetic field amplitudes of the propagating waves compared to \(H_{0}\) in the Lorentz force law.
(b) Solve for each component of the current density \(\textbf{J}\) in terms of the charge velocity components assuming that the propagating waves vary sinusoidally with time as \(e^{j\omega t}\).
Hint: Define
\(\omega _{p}^{2}=\frac{q^{2}n}{m\varepsilon },\quad \omega _{0}=\frac{q\mu _{0}H_{0}}{m}\)
(c) Use the results of (b) in Maxwell's equations for fields of the form \(e^{j\left ( \omega t-kz \right )}\) to solve for the wavenumber \(k\) in terms of \(\omega\).
(d) At what frequencies is the wavenumber zero or infinite? Over what frequency range do we have evanescence or propagation?
(e) For each of the two modes found in (c), what is the polarization of the electric field?
(f) What is the phase velocity of each wave? Since each mode travels at a different speed, the atmosphere acts like an aniso tropic birefringent crystal. A linearly polarized wave \(E_{0}e^{j\left ( \omega t-k_{0}z \right )}\textbf{i}_{x}\) is incident upon such a medium. Write this field as the sum of right and left circularly polarized waves.
Hint:
\(E_{0}\textbf{i}_{x}=\frac{E_{0}}{2}\left ( \textbf{i}_{x}+j\textbf{i}_{y} \right )+\frac{E_{0}}{2}\left ( \textbf{i}_{x}-j\textbf{i}_{y} \right )\)
(g) If the transmitted field at \(z=0\) just inside the medium has amplitude \(E_{t}e^{j\omega t}\textbf{i}_{x}\), what are the electric and magnetic fields throughout the medium?
Nitrobenzene with \(\mu =\mu _{0}\) and \(\varepsilon =35\varepsilon _{0}\) is placed between parallel plate electrodes of spacing \(s\) and length \(l\) stressed by a dc voltage \(V_{0}\). Measurements have shown that light polarized parallel to the dc electric field travels at the speed \(c_{\parallel }\), while light polarized perpendicular to the dc electric field travels slightly faster at the speed \(c_{\perp }\), being related to the dc electric field \(E_{0}\) and free space light wavelength as
\(\frac{1}{c_{\parallel }}+\frac{1}{c_{\perp }}=\lambda BE_{0}^{2}\)
where \(B\) is called the Kerr constant which for nitrobenzene is \(B\approx 4.3\times 10^{-12}\,\textrm{sec/V}^{2} \) at \(\lambda =500\,\textrm{nm}\).
(a) Linearly polarized light with free space wavelength \(\lambda =500\,\textrm{nm}\) is incident at \(45^{\circ }\) to the dc electric field. After exiting the Kerr cell, what is the phase difference between the field components of the light parallel and perpendicular to the dc electric field?
(b) What are all the values of electric field strengths that allow the Kerr cell to act as a quarter- or half-wave plate?
(c) The Kerr cell is placed between crossed polarizers (polariscope). What values of electric field allow maximum light transmission? No light transmission?
Section 7.5
A uniform plane wave with \(y\)-directed electric field is normally incident upon a plasma medium at \(z = 0\) with constitutive law \(\partial \textbf{J}_{f}/\partial t=\omega _{p}^{2}\varepsilon \textbf{E}\). The fields vary sinusoidally in time as \(e^{j\omega t}\).
(a) What is the general form of the incident, reflected, and transmitted fields?
(b) Applying the boundary conditions, find the field amplitudes.
(c) What is the time-average electromagnetic power density in each region for \(\omega > \omega _{p}\), and for \(\omega < \omega _{p}\)?
A polarizing filter to microwaves is essentially formed by many highly conducting parallel wires whose spacing is much smaller than a wavelength. That polarization whose electric field is transverse to the wires passes through. The incident electric field is
\(\textbf{E}=E_{x}\cos \left ( \omega t-kz \right )\textbf{i}_{x}+E_{y}\sin \left ( \omega t-kz \right )\textbf{i}_{y}\)
(a) What is the incident magnetic field and incident power density?
(b) What are the transmitted fields and power density?
(c) Another set of polarizing wires are placed parallel but a distance \(d\) and orientated at an angle \(\phi \) to the first. What are the transmitted fields?
A uniform plane wave with \(y\)-directed electric field \(E_{y}=E_{0}\cos \omega \left ( t-z/c \right )\) is normally incident upon a perfectly conducting plane that is moving with constant velocity \(v\textbf{i}_{z}\), where \(v\ll c\).
(a) What are the total electric and magnetic fields in each region?
(b) What is the frequency of the reflected wave?
(c) What is the power flow density? Why can't we use the complex Poynting vector to find the time-average power?

Section 7.6
A dielectric \(\left ( \varepsilon _{2},\mu _{2} \right )\) of thickness \(d\) coats a perfect conductor. A uniform plane wave is normally incident onto the coating from the surrounding medium with properties \(\left ( \varepsilon _{1},\mu _{1} \right )\).
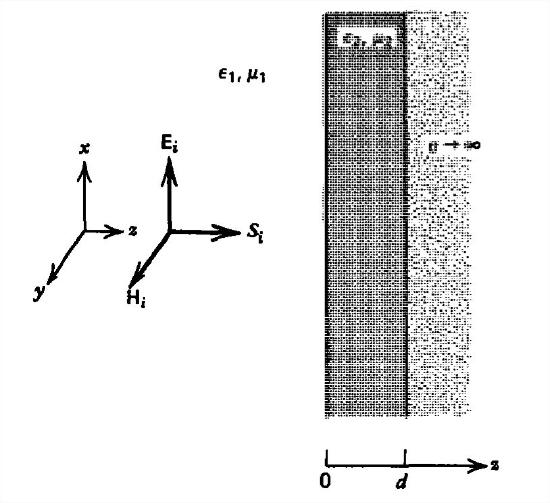
(a) What is the general form of the fields in the two dielectric media? (Hint: Why can the transmitted electric field be written as \(\textbf{E}_{t}=\textrm{Re}\left [ \hat{E}_{t}\sin k_{2}\left ( z-d \right )e^{j\omega t}\textbf{i}_{x} \right ]?\))
(b) Applying the boundary conditions, what are the field amplitudes?
(c) What is the time-average power flow in each region?
(d) What is the time-average radiation pressure on the conductor?
Section 7.7
An electric field of the form \(\textbf{Re}\left ( \hat{E}e^{j\omega t}e^{-\pmb{\gamma } \cdot \textbf{r}} \right )\) propagates in a lossy conductor with permittivity \(\varepsilon \), permeability \(\mu \), and conductivity \(\sigma \). If \(\boldsymbol{\gamma }=\boldsymbol{\alpha }+j\textbf{k}\), what equalities must \(\boldsymbol{\alpha }\) and \(\textbf{k}\) obey?
A sheet of surface charge with charge density \(\sigma _{0}\sin \left ( \omega t-k_{x}x \right )\) is placed at \(z =0\) within a linear medium with properties \(\left ( \varepsilon ,\mu \right )\).
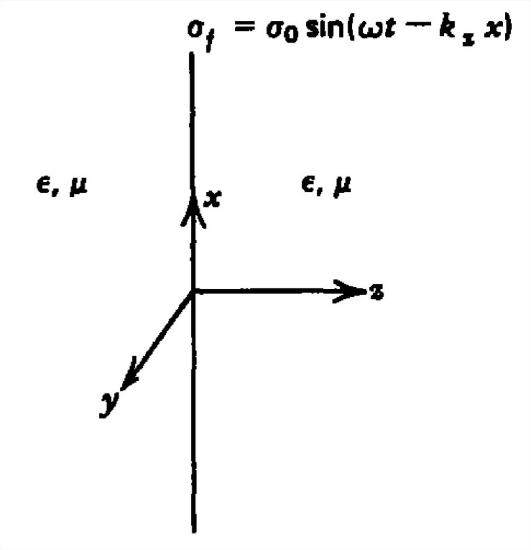
(a) What are the electric and magnetic fields?
(b) What surface current flows on the sheet?
A current sheet of the form \(\textrm{Re}\left ( K_{0}e^{j\left ( \omega t-k_{x}x \right )}\textbf{i}_{x}\right )\) is located in free space at \(z =0\). A dielectric medium \(\left ( \varepsilon ,\mu \right )\) of semi-infinite extent is placed at \(z=d\).
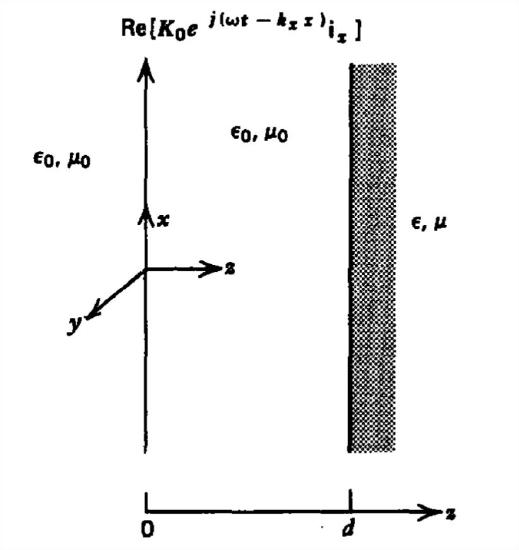
(a) For what range of frequency can we have a nonuniform plane wave in free space and a uniform plane wave in the dielectric? Nonuniform plane wave in each region? Uniform plane wave in each region?
(b) What are the electric and magnetic fields everywhere?
(c) What is the time-average \(z\)-directed power flow density in each region if we have a nonuniform plane wave in free space but a uniform plane wave in the dielectric?
Section 7.8
A uniform plane wave \(\textrm{Re}\left ( E_{0}e^{j\left ( \omega t-k_{x}x-k_{z}z \right )} \textbf{i}_{y}\right )\) is obliquely incident upon a right-angled perfectly conducting corner. The wave is incident at angle \(\theta _{i}\) to the \(z =0\) wall.
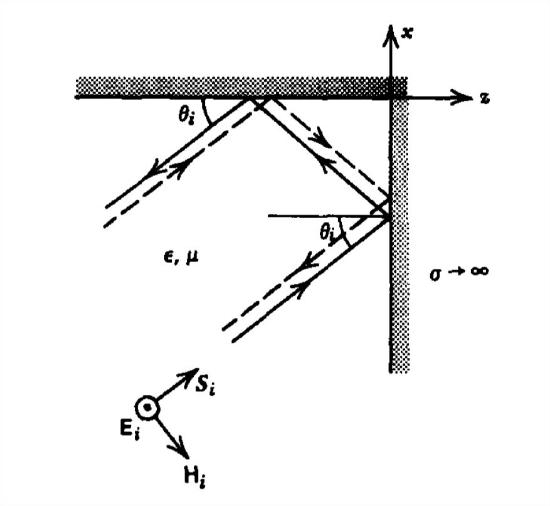
(a) Try a solution composed of the incident and reflected waves off each surface of the conductor. What is the general form of solution? (Hint: There are four different waves.)
(b) Applying the boundary conditions, what are the electric and magnetic fields?
(c) What are the surface charge and current distributions on the conducting walls?
(d) What is the force per unit area on each wall?
(e) What is the power flow density?
Section 7.9
Fermat's principle of least time states that light, when reflected or refracted off an interface, will pick the path of least time to propagate between two points.
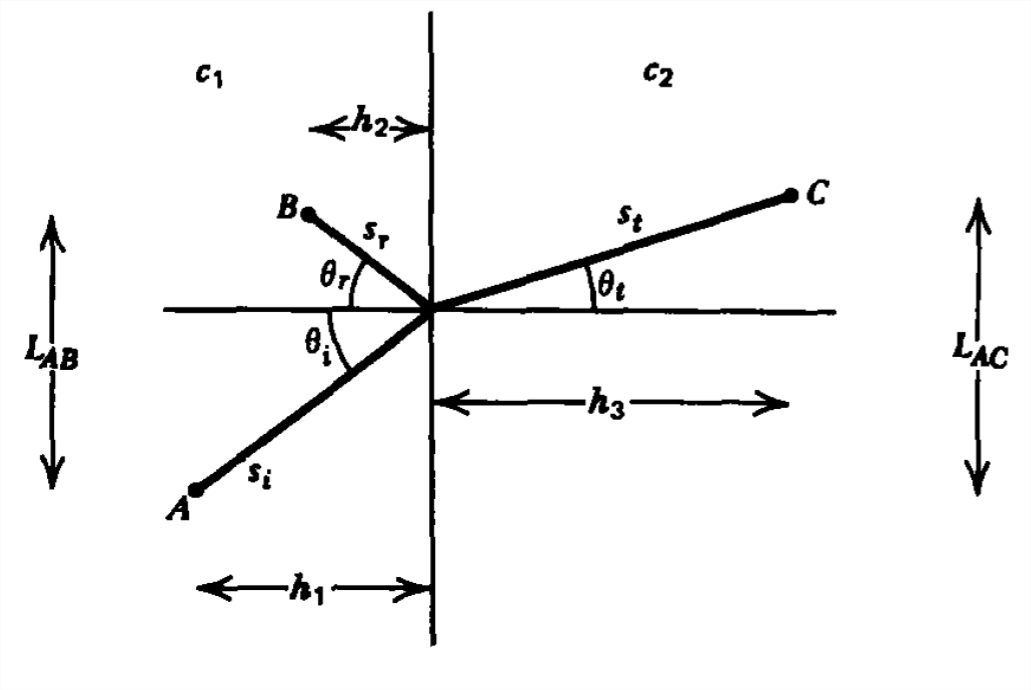
(a) A beam of light from point \(A\) is incident upon a dielectric interface at angle \(\theta _{i}\), from the normal and is reflected through the point \(B\) at angle \(\theta _{r}\). In terms of \(\theta _{i}\), \(\theta _{r}\), \(h_{1}\) and \(h_{2}\), and the speed of light \(c_1\), how long does it take light to travel from \(A\) to \(B\) along this path? What other relation is there between \(\theta _{i}\), \(\theta _{r}\), \(L_{AB}\), \(h_{1}\)and \(h_{2}\)?
(b) Find the angle \(\theta _{i}\) that satisfies Fermat's principle. What is \(\theta _{r}\)?
(c) In terms of \(\theta _{i}\), \(\theta _{r}\), \(h_{1}\), \(h_{3}\), and the light speeds \(c_{1}\) and \(c_{2}\) in each medium, how long does it take light to travel from \(A\) to \(C\)?
(d) Find the relationship between \(\theta _{i}\) and \(\theta _{r}\) that satisfies Fermat's principle.
In many cases the permeability of dielectric media equals that of free space. In this limit show that the reflection and transmission coefficients for waves obliquely incident upon dielectric media are: \(\textbf{E}\) parallel to the interface
\(R=-\frac{\sin \left ( \theta _{i}-\theta _{t} \right )}{\sin \left ( \theta _{i}+\theta _{t} \right )},\quad T=\frac{2\cos \theta _{i}\sin \theta _{t}}{\sin \left ( \theta _{i}+\theta _{t} \right )}\)
\(\textbf{H}\) parallel to the interface
\(R=\frac{\tan \left ( \theta _{i}-\theta _{t} \right )}{\tan \left ( \theta _{i}+\theta _{t} \right )},\quad T=\frac{2\cos \theta _{i}\sin \theta _{i}}{\sin \left ( \theta _{i}+\theta _{t} \right )\cos \left ( \theta _{i}-\theta _{t} \right )}\)
White light is composed of the entire visible spectrum. The index of refraction \(n\) for most materials is a weak function of wavelength \(\lambda \), often described by Cauchy's equation
\(n=A+B/\lambda ^{2}\)
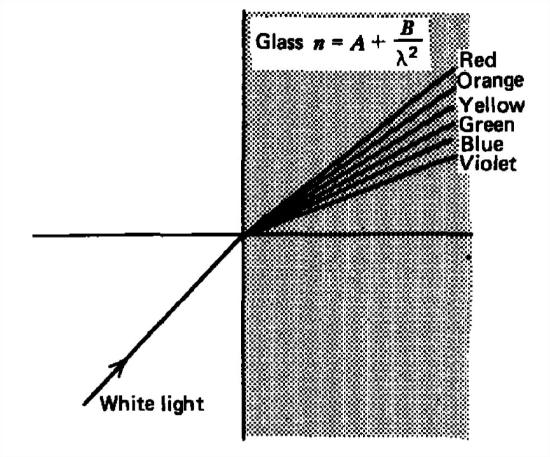
A beam of white light is incident at \(30^{\circ }\) to a piece of glass with \(A=1.5\) and \(B=5\times 10^{-15}\,\textrm{m}^{2}\). What are the transmitted angles for the colors violet \(\left ( 400\,\textrm{nm} \right )\), blue \(\left ( 440\,\textrm{nm} \right )\), green \(\left ( 550\,\textrm{nm} \right )\), yellow \(\left ( 600\,\textrm{nm} \right )\), orange \(\left ( 650\,\textrm{nm} \right )\), and red \(\left ( 700\,\textrm{nm} \right )\)? This separation of colors is called dispersion.
A dielectric slab of thickness \(d\) with speed of light \(c_{2}\) is placed within another dielectric medium of infinite extent with speed of light \(c_{1}\), where \(c_{1}< c_{2}\). An electromagnetic wave with \(\textbf{H}\) parallel to the interface is incident onto the slab at angle \(\theta_{i}\).
(a) Find the electric and magnetic fields in each region. (Hint: Use Cramer's rule to find the four unknown field amplitudes in terms of \(E_{i}\).)
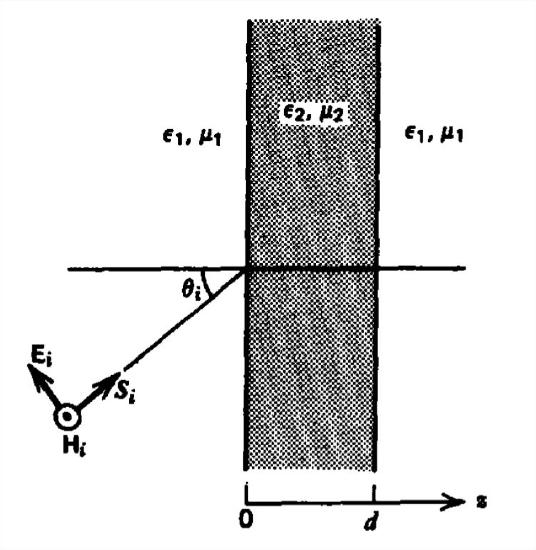
(b) For what range of incident angle do we have uniform or nonuniform plane waves through the middle region?
(c) What is the transmitted time-average power density with uniform or nonuniform plane waves through the middle region. How can we have power flow through the middle region with nonuniform plane waves?
Section 7.10
Consider the various prisms shown.

(a) What is the minimum index of refraction \(n_{1}\) necessary for .no time-average power to be transmitted across the hypotenuse when the prisms are in free space, \(n_{2}=1\), or water, \(n_{2}=1.33\)?
(b) At these values of refractive index, what are the exiting angles \(\theta _{e}\)?
A fish below the surface of water with index of refraction \(n=1.33\) sees a star that he measures to be at \(30^{\circ }\) from the normal. What is the star's actual angle from the normal?

A straight light pipe with refractive index \(n_{1}\) has a dielectric coating with index \(n_{2}\) added for protection. The light pipe is usually within free space so that \(n_{3}\) is typically unity.
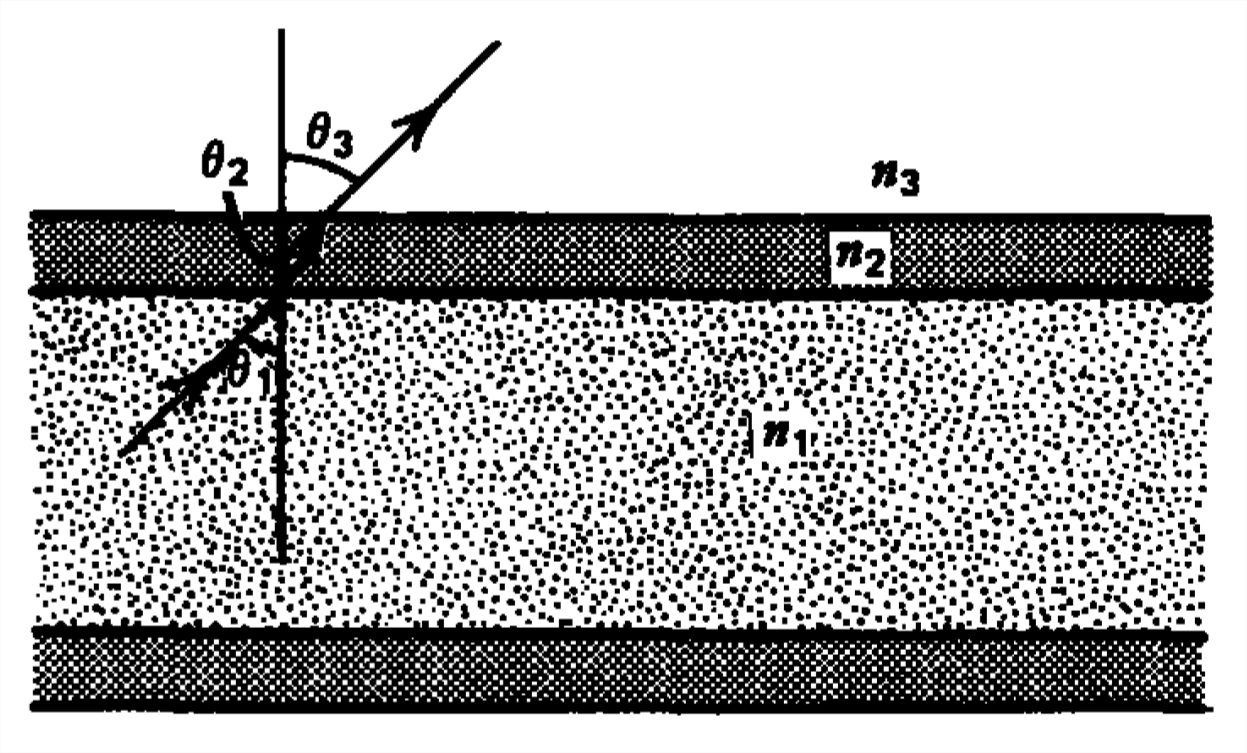
(a) Light within the pipe is incident upon the first interface at angle \(\theta _{1}\). What are the angles \(\theta _{2}\) and \(\theta _{3}\)?
(b) What value of \(\theta _{1}\) will make \(\theta _{3}\) just equal the critical angle for total internal reflection at the second interface?
(c) How does this value differ from the critical angle if the coating was not present so that \(n_{1}\) was directly in contact with \(n_{3}\)?
(d) If we require that total reflection occur at the first interface, what is the allowed range of incident angle \(\theta _{1}\). Must the coating have a larger or smaller index of refraction than the light pipe?
A spherical piece of glass of radius \(R\) has refractive index \(n\).
(a) A vertical light ray is incident at the distance \(x\,\left ( x< R \right )\) from the vertical diameter. At what distance \(y\) from the top of the sphere will the light ray intersect the vertical diameter? For what range of \(n\) and \(x\) will the refracted light intersect the vertical diameter within the sphere?
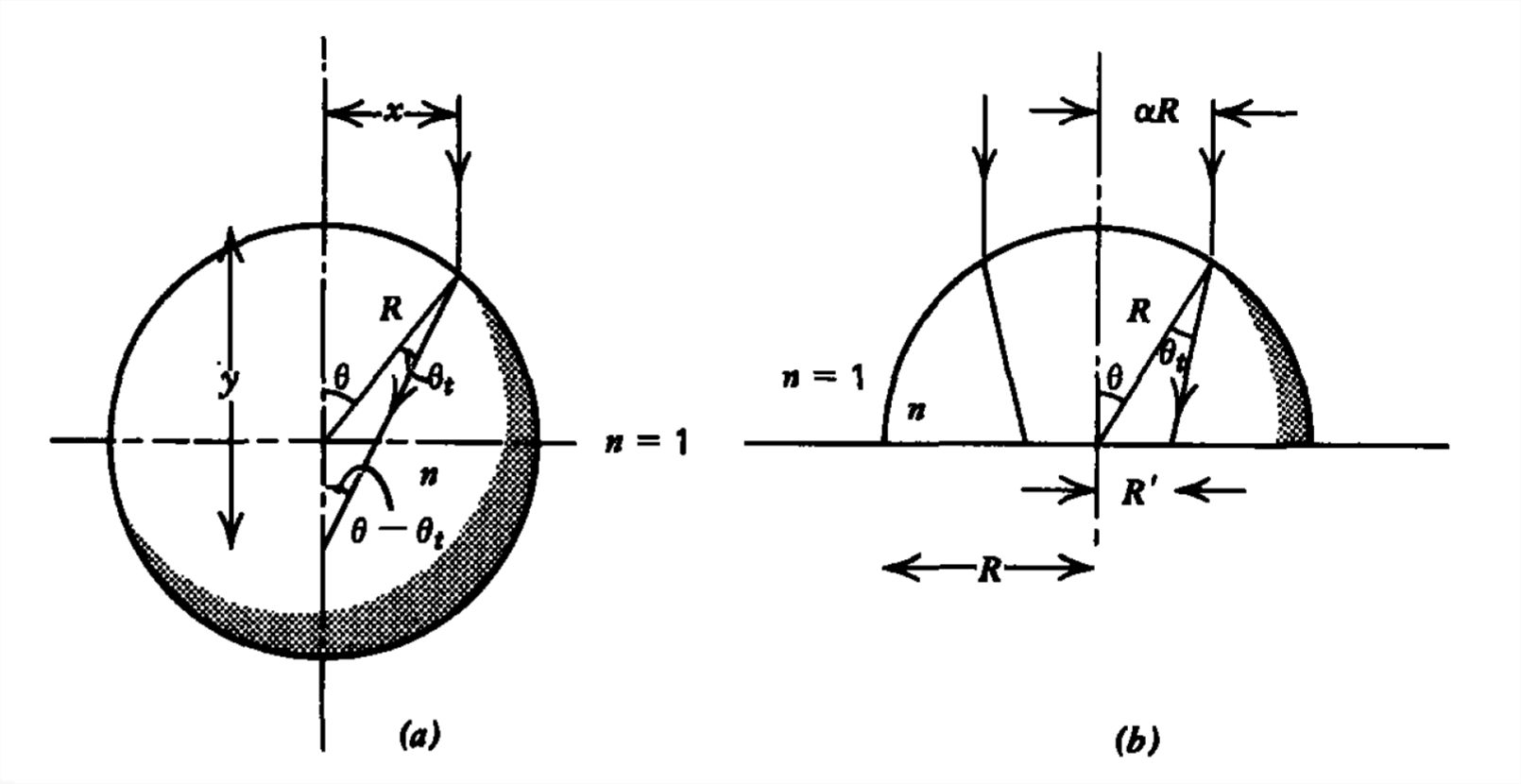
(b) A vertical light beam of radius \(\alpha R\,\left ( \alpha < 1 \right )\) is incident upon a hemisphere of this glass that rests on a table top. What is the radius \(R'\) of the light on the table?


