1.5: Loop and Node Equations

Last updated
Save as PDF

Page ID: 55511

James Kirtley
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

There are two well- developed formal ways of solving for the potentials and currents in networks, often referred to as loop and node equation methods. They are closely related, using KCL and KVL together with element constraints to build sets of equations which may then be solved for potentials and currents.

In the node equation method, KCL is written at each node of the network, with currents expressed in terms of the node potentials. KVL is satisfied because the node potentials are unique.
In the loop equation method, KVL is written about a collection of closed paths in the network. “Loop currents” are defined, and made to satisfy KCL, and the branch voltages are expressed in terms of them.

The two methods are equivalent and a choice between them is usually a matter of personal preference. The node equation method is probably more widely used, and lends itself well to computer analysis.

To illustrate how these methods work, consider the network of Figure 12.

This network has three nodes. We are going to write KCL for each of the nodes, but note that only two explicit equations are required. If KCL is satisfied at two of the nodes, it is automatically satisfied at the third. Usually the datum node is the one for which we do not write the expression.

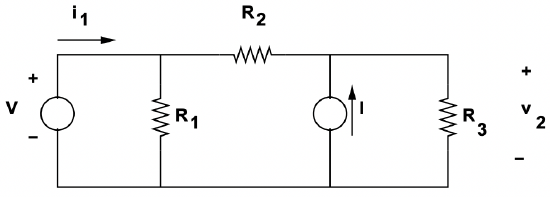Screen Shot 2021-07-19 at 10.26.59 AM.png

KCL written for the two upper nodes of the network is:

\[\ -i_{1}+\frac{V}{R_{1}}+\frac{V-v_{2}}{R_{2}}=0\label{9} \]

\[\ -I+\frac{v_{2}-V}{R_{2}}+\frac{v_{2}}{R_{3}}=0\label{10} \]

These two expressions are easily solved for the two unknowns, \(\ i_{1}\) and \(\ v_{2}\):

\(\ \begin{array}{c}
v_{2}=\frac{R_{3}}{R_{2}+R_{3}} V+\frac{R_{2} R_{3}}{R_{2}+R_{3}} I \\
i_{1}=\frac{R_{1}+R_{2}+R_{3}}{R_{1}\left(R_{2}+R_{3}\right)} V-\frac{R_{3}}{R_{2}+R_{3}} I
\end{array}\)

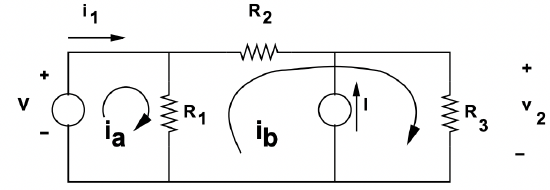Screen Shot 2021-07-19 at 10.33.23 AM.png

The loop equation method is similar. We need the same number of independent expressions (two), so we need to take two independent loops. For this, take as the loops as is shown in Figure 13:

The loop that includes the voltage source and \(\ R_{1}\).
The loop that includes \(\ R_{1}, R_{2}\), and \(\ R_{3}\).

It is also necessary to define loop currents, which we will denote as \(\ i_{a}\) and \(\ i_{b}\). These are the currents circulating around the two loops. Note that where the loops intersect, the actual branch current will be the sum of or difference between loop currents. For this example, assume the loop currents are defined to be circulating counter-clockwise in the two loops. The two loop equations are:

\[\ V+R_{1}\left(i_{a}-i_{b}\right)=0\label{11} \]

\[\ R_{1}\left(i_{b}-i_{a}\right)+R_{2} i_{b}+R_{3}\left(i_{b}-I\right)=0\label{12} \]

These are equally easily solved for the two unknowns, in this case the two loop currents \(\ i_{a}\) and \(\ i_{b}\).