1.6: Linearity and Superposition

Last updated
Save as PDF

Page ID: 55512

James Kirtley
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

An extraordinarily powerful notion of network theory is linearity. This property has two essential elements, stated as follows:

For any single input \(\ x\) yielding output \(\ y\), the response to an input \(\ k x\) is \(\ k y\) for any value of \(\ k\).
If, in a multi-input network the input \(\ x_{1}\) by itself yields output \(\ y_{1}\) and a second input \(\ x_{2}\) by itself yields \(\ y_{2}\), then the combination of inputs \(\ x_{1}\) and \(\ x_{2}\) yields the output \(\ y=y_{1}+y_{2}\).

This is important to us at the present moment for two reasons:

It tells us that the solution to certain problems involving networks with multiple inputs is actually easier than we might expect: if a network is linear, we may solve for the output with each separate input, then add the outputs. This is called superposition.
It also tells us that, for networks that are linear, it is not necessary to actually consider the value of the inputs in calculating response. What is important is a system function, or a ratio of output to input.

Superposition is an important principle when dealing with linear networks, and can be used to make analysis easier. If a network has multiple independent sources, it is possible to find the response to each source separately, then add up all of the responses to find total response. Note that this can only be done with independent sources!

Consider, for example, the example circuit shown in Figure 12. If we are only interested in the output voltage \(\ v_{2}\), we may find the response to the voltage source first, then the response to the current source, then the total response is the sum of the two. To find the response to the voltage source, we must “turn off” the current source. This is done by assuming that it is not there. (After all, a current source with zero current is just an open circuit!). The resulting network is as in Figure 14.

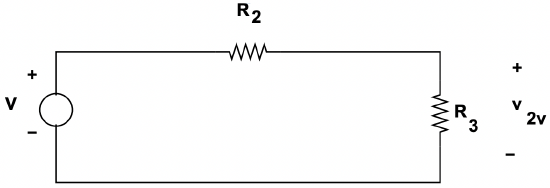Screen Shot 2021-07-19 at 10.54.48 AM.png

Note that the resistance \(\ R_{1}\) does not appear here. This is because a resistance in parallel with a voltage source is just a voltage source, unless one is interested in current in the resistance. The output voltage is just:

\(\ v_{2 v}=V \frac{R_{3}}{R_{2}+R_{3}}\)

Next, we “turn off” the voltage source and “turn on” the current source. Note that a voltage source that has been turned off is a short circuit, because that implies zero voltage. The network is as shown in Figure 15

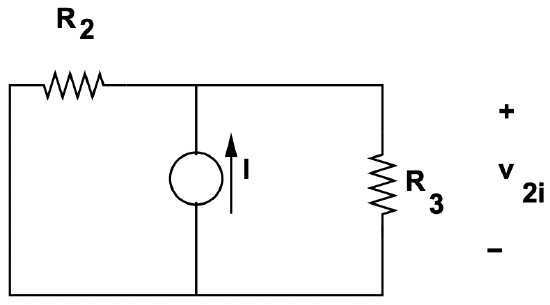Screen Shot 2021-07-19 at 10.56.29 AM.png

The response to this is:

\(\ v_{2 i}=I R_{2} \| R_{3}\)

The total response is then just:

\(\ v_{2}=v_{2 v}+v_{2 i}=V \frac{R_{3}}{R_{2}+R_{3}}+I \frac{R_{2} R_{3}}{R_{2}+R_{3}}\)