6.1: Electric Circuits and Kirchoff’s Laws

Last updated
Save as PDF

Page ID: 55586

James Kirtley
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Conservation of Charge and KCL

To begin with, consider the law of Conservation of Charge:

\(\ \oiint \vec{J} \cdot d \vec{a}=\frac{d}{d t} \int_{\mathrm{vol}} q d v=0\)

This assumes, of course, that there is no accumulation of charge anywhere in the system. This is not a wonderful assumption for any systems with capacitor plates, but if one considers capacitors to be circuit elements so that both plates of a capacitor are part of any given element the right hand side of this expression really is zero.

Thsn, if we note current to be the integral of current density: Over some area, a fraction of the whole area around a node:

\(\ i_{k}=\iint_{A_{k}} \vec{J} \cdot d \vec{a}\)

then we have:

\(\ \sum_{k} i_{k}=0\)

Faraday’s Law

\(\ \oint \vec{E} \cdot d \vec{\ell}=-\frac{d}{d t} \iint \vec{B} \cdot d \vec{a}\)

The left-hand integral may be taken to be a number of sub-integrals, each denoted by a discrete fractional integral:

\(\ v_{k}=\int_{a_{k}}^{b_{k}} \vec{E} \cdot d \ell\)

If we assume that there are no substantive flux linkages among the circuit elements:

\(\ \iint \vec{B}=0\)

then we have KVL:

\(\ \sum_{k} v_{k}=0\)

Faraday’s Law

\(\ \oint \vec{E} \cdot d \vec{\ell}=-\frac{d}{d t} \iint \vec{B} \cdot d \vec{a}\)

The left-hand integral may be taken to be a number of sub-integrals, each denoted by a discrete fractional integral:

\(\ v_{k}=\int_{a_{k}}^{b_{k}} \vec{E} \cdot d \ell\)

If we assume that there are no substantive flux linkages among the circuit elements:

\(\ \iint \vec{B}=0\)

then we have KVL:

\(\ \sum_{k} v_{k}=0\)

Ohm’s Law

At this point it is probably appropriate to note that Ohm’s Law can be used to derive the constitutive relationship for a resistor. Suppose we have a conductive element similar to the rectangular solid shown in Figure 1. Assume current is confined in this element and flowing perpendicular to the flat end shown in the figure. Current density is

\(\ J_{x}=\frac{I}{h w}\)

where I is to total current and h and w are height and width of the conductor, respectively. Electric field along the length of the element is:

\(\ E_{x}=\frac{J_{x}}{\sigma}\)

where \(\ \sigma\) is the electrical conductivity of the material. Voltage developed is:

\(\ v_{k}=\int E_{x} d \ell=\frac{J_{x}}{\sigma} l\)

Which leads us to an expression for element resistance:

\(\ R=\frac{v}{I}=\frac{l}{h w \sigma}\)

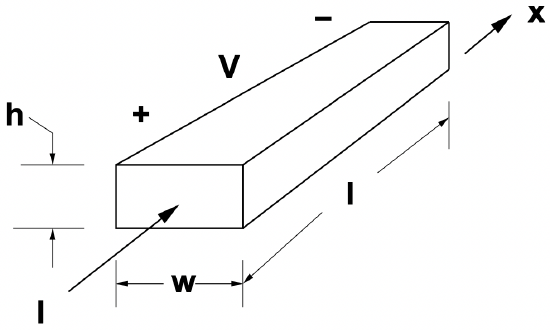Screen Shot 2021-07-21 at 4.09.26 PM.png