9.10: Wilkinson Combiner and Divider

A combiner is used to combine power from two or more sources. A typical use is to combine power from two high power amplifiers to obtain a higher power than would be otherwise be available. Dividers divide power so that the power from an amplifier can be routed to different parts of a circuit.

The Wilkinson divider can be used as a combiner or divider that divides input power among the output ports [14]. Figure \(\PageIndex{1}\)(a) is a two-way divider that splits the power at Port \(1\) equally between the two output ports at Ports \(2\) and \(3\). A particular insight that Wilkinson brought was the introduction of the resistor between the output ports and this acts to suppress any imbalance between the output signals due to nonidealities. If the division is exact, no current will flow in the resistor. The circuit works less well as a general purpose combiner. Ideally power entering Ports \(2\) and \(3\) would combine losslessly and appear at Port \(1\). A typical application is to combine the power at the output of two matched transistors where the amplitude and the phase of the signals can be expected to be closely matched. However, if the signals are not identical, the portion that is mismatched will be absorbed in the resistor. The bandwidth of the Wilkinson combiner/divider is limited by the one-quarter wavelength long lines.

The \(S\) parameters of the two-way Wilkinson power divider with an equal split of the output power are therefore

\[\label{eq:1}\mathbf{S}=\left[\begin{array}{ccc}{0}&{-\jmath /\sqrt{2}}&{-\jmath /\sqrt{2}}\\{-\jmath /\sqrt{2}}&{0}&{0}\\{-\jmath /\sqrt{2}}&{0}&{0}\end{array}\right] \]

Figure \(\PageIndex{1}\)(b) is a compact representation of the two-way Wilkinson divider, and a three-way Wilkinson divider is shown in Figure \(\PageIndex{1}\)(d). This pattern can be repeated to produce \(N\)-way power dividing. The lumped-element version of the Wilkinson divider shown in Figure \(\PageIndex{1}\)(c) is based on the \(LC\) model of a one-quarter wavelength long transmission line segment. With a \(50\:\Omega\) system impedance and center frequency of \(400\text{ MHz}\), the elements of the lumped element are (from Section 22.7.2 of [15]) \(L = 28.13\text{ nH},\: C_{1} = 11.25\text{ pF},\: C_{2} = 5.627\text{ pF},\) and \(R = 100\:\Omega\).

Figure \(\PageIndex{2}\)(a) is the layout of a direct microstrip realization of a Wilkinson divider. A high-performance microstrip layout is shown in Figure \(\PageIndex{2}\)(b), where the transmission lines are curved to bring the output ports near each other so that a chip resistor can be used.

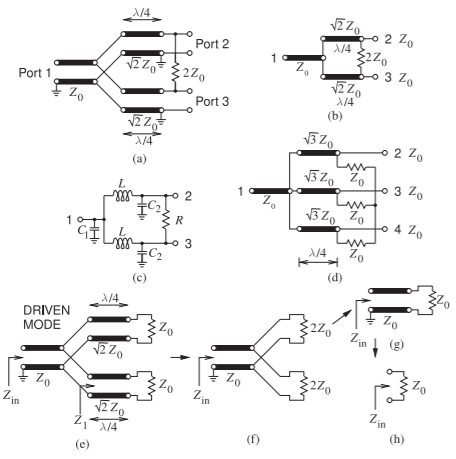
Figure \(\PageIndex{1}\): Wilkinson divider: (a) two-way divider with Port \(1\) being the combined signal and Ports \(2\) and \(3\) being the divided signals; (b) less cluttered representation; (c) lumped-element implementation; (d) three-way divider with Port \(1\) being the combined signal and Ports \(2\), \(3\), and \(4\) being the divided signals; and (e)–(h) steps in the derivation of the input impedance.

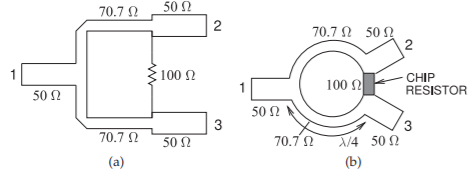
Figure \(\PageIndex{2}\): Wilkinson combiner and divider: (a) microstrip realization; and (b) higher performance microstrip implementation.

Example \(\PageIndex{1}\): Lumped-Element Wilkinson Divider

Design a lumped-element \(2\)-way Wilkinson divider in a \(60\:\Omega\) system. The center frequency of the design should be \(10\text{ GHz}\).

Solution

The design begins with the transmission line form of the Wilkinson divider which will be converted to a lumped-element form latter. The design parameters are \(Z_{0} = 60\:\Omega ,\: f = 10\text{ GHz},\:\omega = 2\pi 10^{10} = 2.283\cdot 10^{10}\) and so

\[Z_{01}=\sqrt{2}Z_{0}=84.85\:\Omega ,\quad R=2Z_{0}=120\:\Omega\nonumber \]

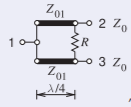
Figure \(\PageIndex{3}\)

The next stage is to convert the transmission lines to lumped elements. A broadband design of a quarter-wavelength transmission line is presented in Section 22.7.2 of [15]. That is, each of the quarter-wave lines has the model

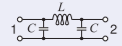
Figure \(\PageIndex{4}\)

with \(L = Z_{01}/\omega = 84.85/\omega = 954.9\text{ pH},\)

\(C = 1/(Z_{01}\omega )=1/(84.85\omega ) = 265.3\text{ fF}.\)

So the final lumped element design is

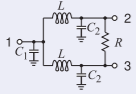
Figure \(\PageIndex{5}\)

with

\(C_{1}=2C=530.6\text{ fF}\),

\(C_{2}=C=265.3\text{ fF}\),

\(L=954.9\text{ pH}\),

\(R=120\:\Omega\).