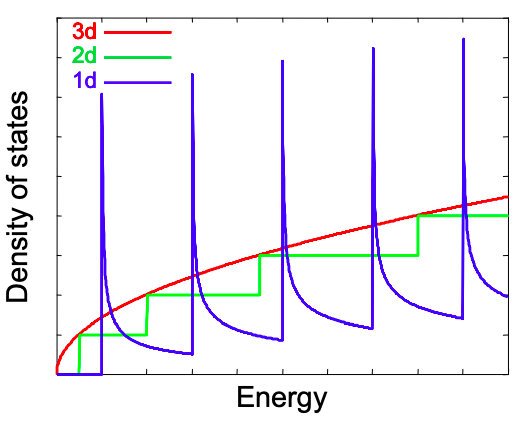
2.14: The 3-d DOS- bulk materials with no confinement
- Page ID
- 50144
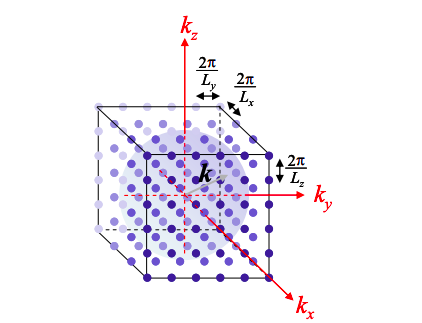
In 3-d, there is no electron confinement. The only constraint on \(k_{x}\), \(k_{y}\), or \(k_{z}\) are the periodic boundary conditions. We have just shown that if the system has volume \(L_{x}\times L_{y}\times L_{z}\) then each allowed value of k-space occupies a volume of \(2\pi/ L_{x}\times 2\pi/L_{y}\times2\pi/L_{z} = 8\pi^{3}/V\).
To determine the number of allowed states, we will integrate over all k-space. It is convenient to do this in spherical coordinates. If k is the magnitude of the k vector, the number of modes within a spherical shell of thickness dk is then
\[ n_{s}(k)dk=2\times \frac{1}{8\pi^{3}/V}\times 4\pi k^{2}dk \nonumber \]
where \(V = L_{x}\times L_{y}\times L_{z}\), and the factor of two accounts for electron spin. The unconfined wavefunctions within our 3-d box are plane waves in all directions, i.e. the wavefunction could be described by
\[ \psi(x,y,z) = \psi_{0}e^{ik_{x}x}e^{ik_{y}y}e^{ik_{z}z} \nonumber \]
Substituting into the Schrödinger Equation gives
\[ -\frac{\hbar^{2}}{2m} \left( \frac{d^{2}}{dx^{2}}\frac{d^{2}}{dy^{2}} \frac{d^{2}}{dx^{2}}\right) \psi = E \psi \nonumber \]
Which gives
\[ \frac{\hbar^{2}}{2m} (k_{x}^{2} + k_{x}^{2}+ k_{x}^{2}) = E \nonumber \]
Rearranging:
\[ E = \frac{\hbar^{2}k^{2}}{2m} \nonumber \]
Using Equation (2.14.5) to relate E to k gives:
\[ g(E)dE = \frac{V}{2\pi^{2}}\left( \frac{2m}{\hbar^{2}}\right)^{\frac{3}{2}} \sqrt{E}\ dE \nonumber \]
where g(E) is the density of states per unit energy.
A comparison of the density of states in 1-d, 2-d and 3-d materials is shown in Figure 2.14.2.